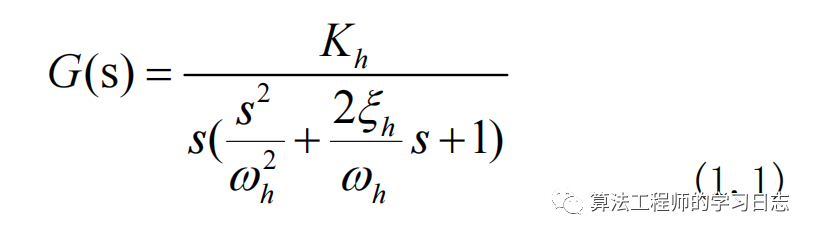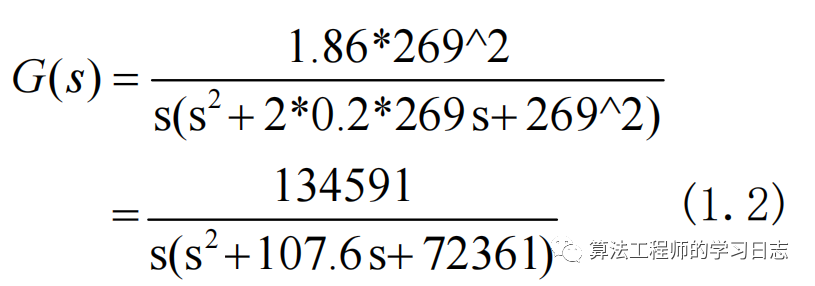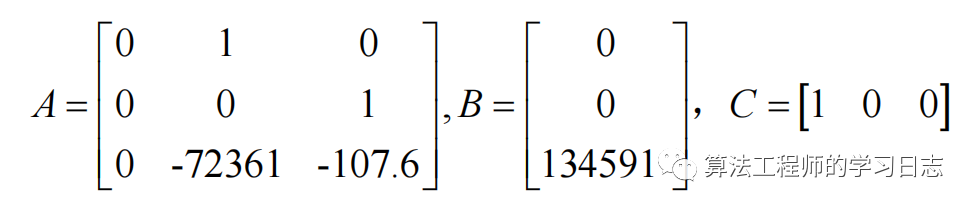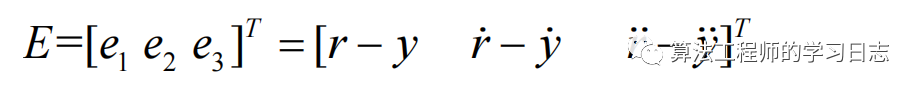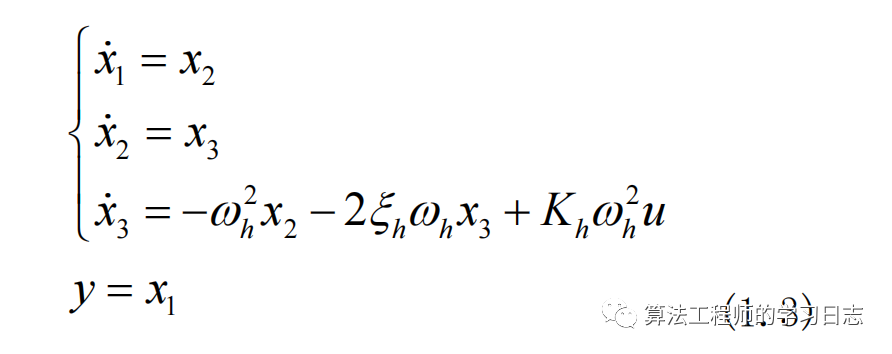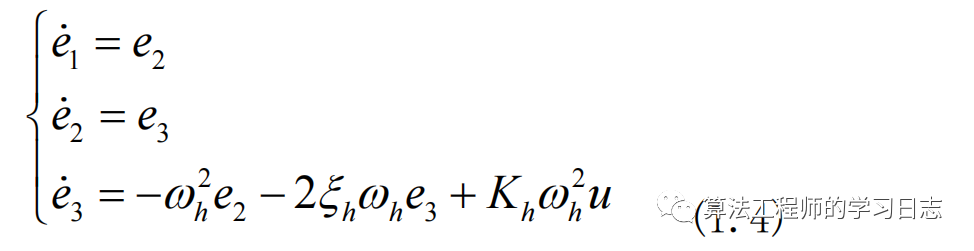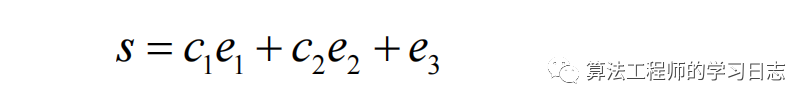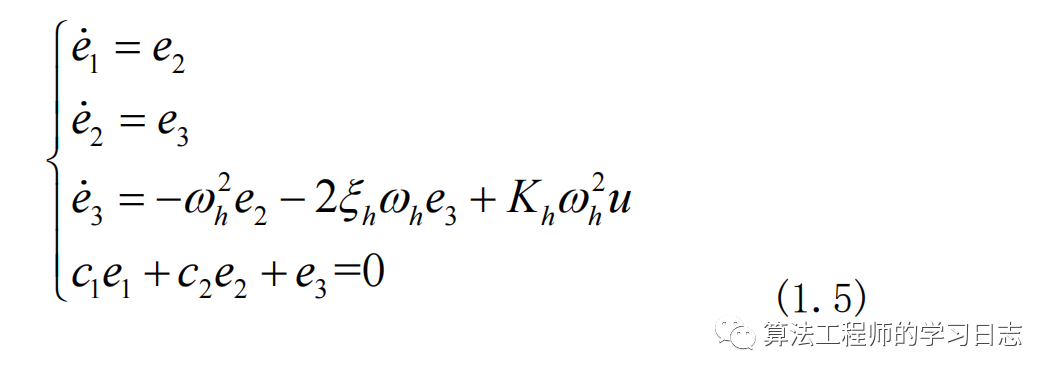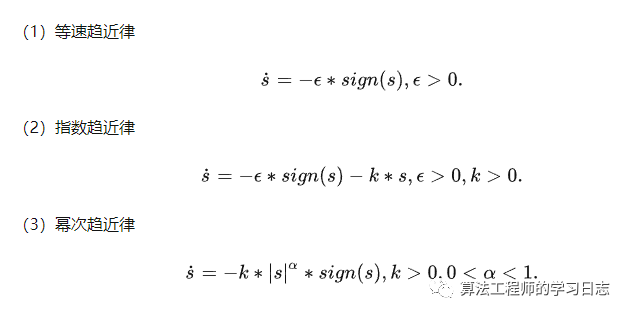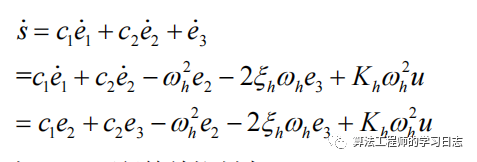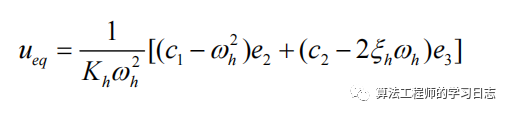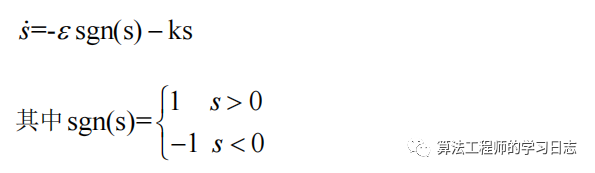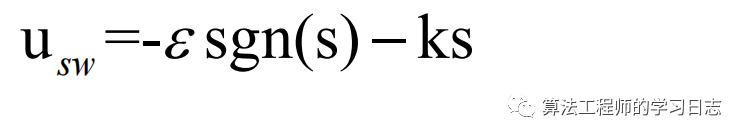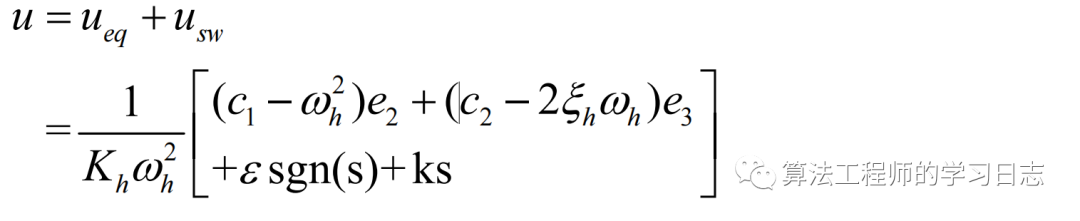前天有个微信好友咨询了一些滑模控制器的设计和理论推导，故整理一下相关的资料和内容分享，

滑模控制的运动轨迹主要分为两个方面：(1)系统的任意初始状态向滑模面运动阶段；(2)系统到达滑模面后并且慢慢趋于稳定的阶段。所以，对于滑模变结构控制器的设计，对应于系统运动的两个阶段，可以分为两个部分：第一部分，滑模面的设计；第二部分，控制律的设计。

0、前言

滑模控制（Sliding Mode Control，SMC）是一种非线性控制方法，其核心思想是通过引入一个滑动模态，使系统状态在该模态上滑动，并保持在滑动面上。滑模控制具有强鲁棒性和快速响应的特点，能够有效应对系统参数不确定性、外部干扰和测量噪声等问题。

滑模控制的基本原理是通过设计一个滑动面，使系统状态在该面上滑动，并且在滑动面上滑动的速度足够快，从而将系统状态迅速带到所期望的工作区域。通常情况下，滑动面由一个或多个状态变量的线性组合构成，可以根据实际应用需求进行选择。

滑模控制的主要步骤包括：

1. 滑动面设计：根据系统的数学模型和控制目标，设计一个合适的滑动面。滑动面应具有良好的鲁棒性和适应性，能够满足所需的控制性能。

2. 控制律设计：根据滑动面的定义，设计一个控制律使得系统状态在滑动面上滑动。通常情况下，控制律包括两个部分：滑动面的控制和滑模调节器。滑动面的控制用来使系统状态迅速进入滑动模态，而滑模调节器用来保持系统状态在滑动面上滑动。

3. 控制器实现：根据设计的控制律，实现具体的控制器。控制器可以是连续时间控制器或离散时间控制器，具体选择取决于被控系统的特性和应用需求。

滑模控制的优点包括：

• 鲁棒性：滑模控制对系统的参数不确定性和外部干扰具有较强的鲁棒性，能够使系统在不确定性和扰动的影响下仍能保持滑动模态。

• 快速响应：由于滑动模态的特性，滑模控制具有快速响应的特点，能够使系统迅速达到所期望的状态。

• 简单性：相对于一些复杂的控制方法，滑模控制比较简单，容易实现和应用。

1、滑模面的设计

以电液伺服控制系统为例，电液伺服控制系统中不考虑伺服阀的非线性影响将其简化为比例环节，所以由电液伺服系统的数学模型可得伺服阀阀芯位移到液压缸活塞位移的传递函数为：

辨识后的模型为

状态空间方程为

被控对象为三阶系统， X = [x x' x'']为系统状态变量。设定r为给定的输入信号， y为系统输出信号，所以系统的误差为 e=r -y,，定义系统的误差向量为：

可以根据系统模型状态空间方程

写出误差状态方程

所设计的滑模切换函数为

滑模运动的微分方程为

其中c1、c2决定了滑动模态的动态品质，可以采用极点置法求得c1、c2  。选择期望极点为-34.4±168.52i,可以得到参数 c1=29582, c2=68.8， 

2、控制器的设计

对于滑模变结构控制器的设计如下： 

u=ueq+usw

ueq是等效控制，能够实现系统状态的跟踪，即将系统的状态一直保持在滑模面上； usw是切换控制，使系统状态趋近于滑模面，削弱系统的抖振，常用的趋近率有三种：

本节将采用指数趋近律,

等效控制部分，对s=c1*e1+c2*e2+e3求导得

根据s'=0可得到等效控制：

切换控制部分，选择指数趋近律，即

假如eta过小，那么趋近的速度很慢，调节的过程太慢；相反，若eta太大，那么系统到达切换面的时候，具有比较大的速度，引起较大的抖动。对于 k，能够加快调节时间，能够快速到达滑模面的过程，还可以削弱抖振，改善系统的品质。本文中，指数趋近律的参数 k 为 20， eta为 5。所以切换控制为：

综上所述，滑模变结构的控制器设计为

3、实例建模和分析

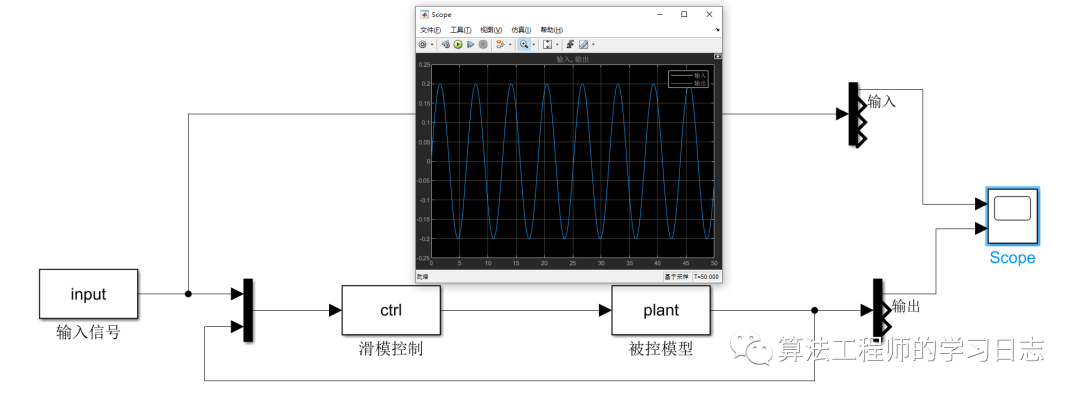
在matlab simulink中用sfunction搭建对应的仿真模型

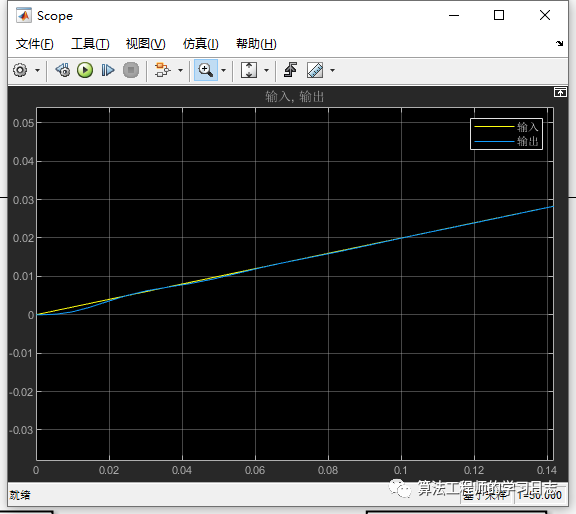
放大结果图，可以看到在滑模控制能够很快的实现输入跟踪，控制效率极高