一、树与图的存储

1.树的特性

树是一种特殊的图,具有以下两个重要特性:

1. 无环
   树是一个无环连通图,这意味着树中任意两个节点之间都存在且仅存在一条简单路径,不存在环路。

2. 连通
   树的所有节点都连通,从任一节点出发都可以达到其他节点。换句话说,树不含孤立的子图,它只有一个连通分量。

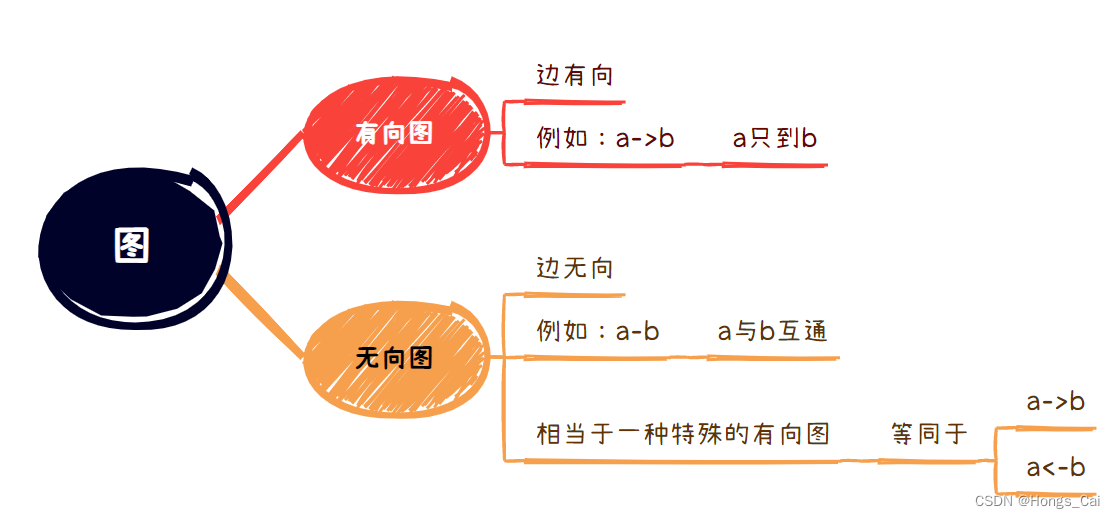
2.图的分类

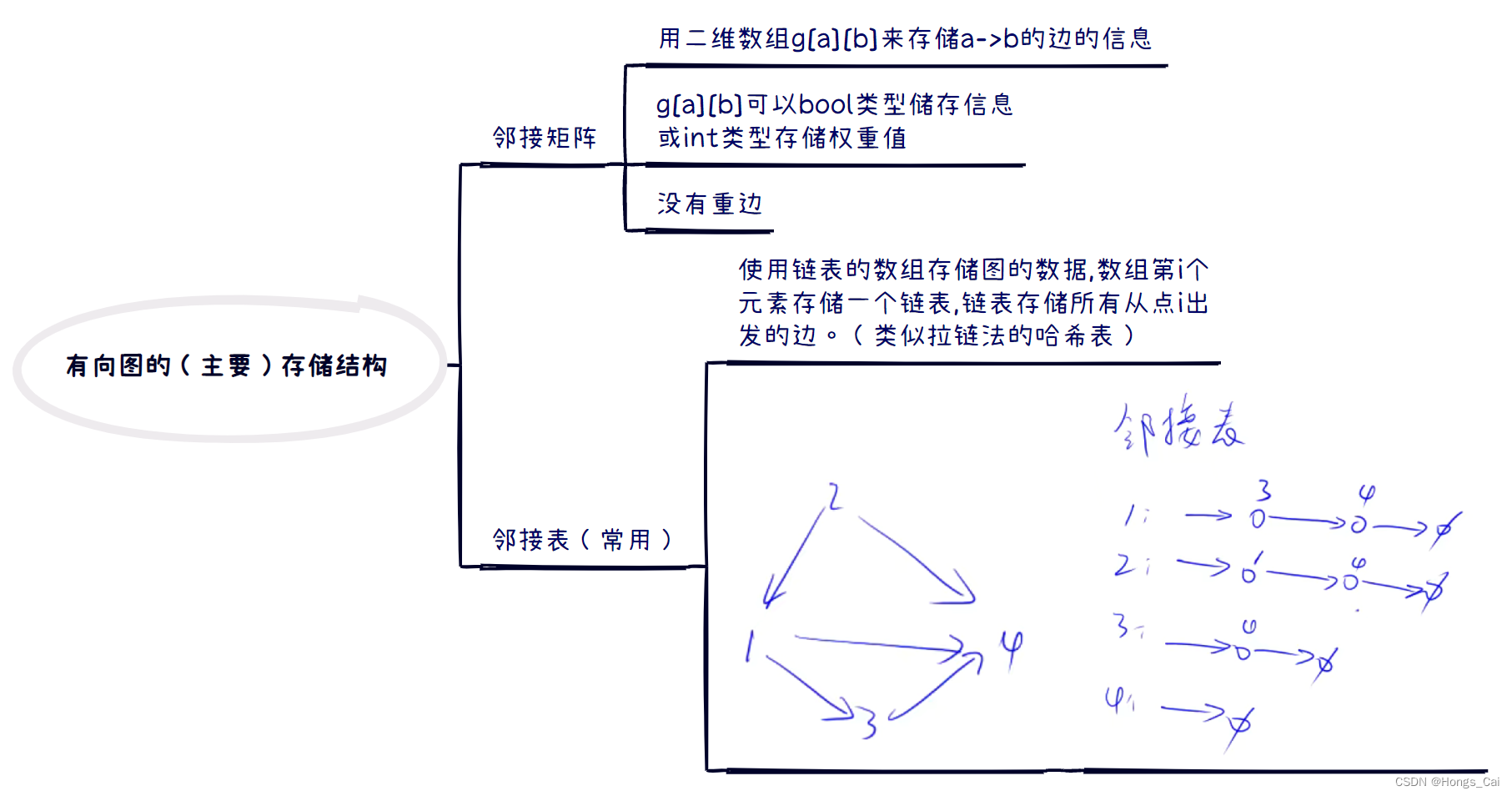
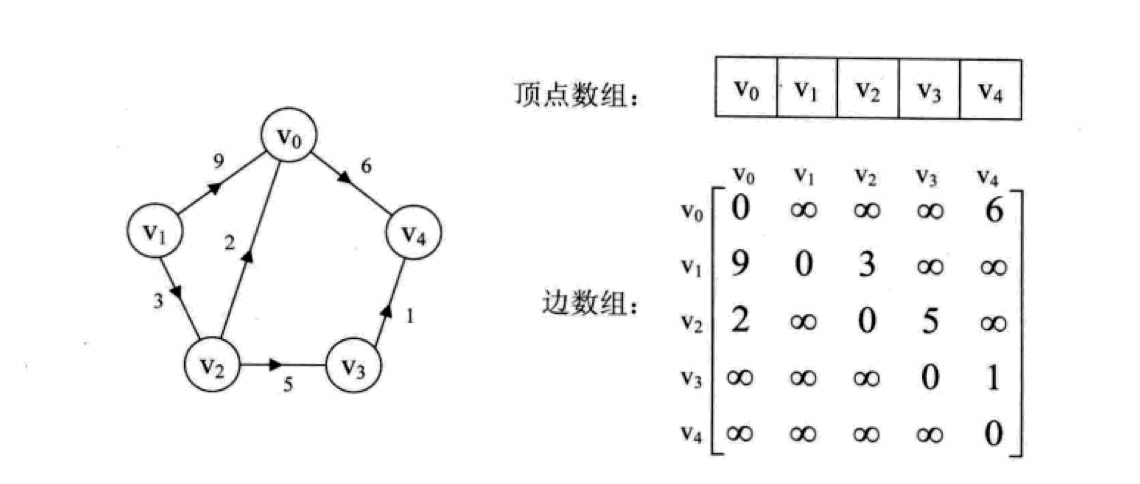
3.有向图的储存结构

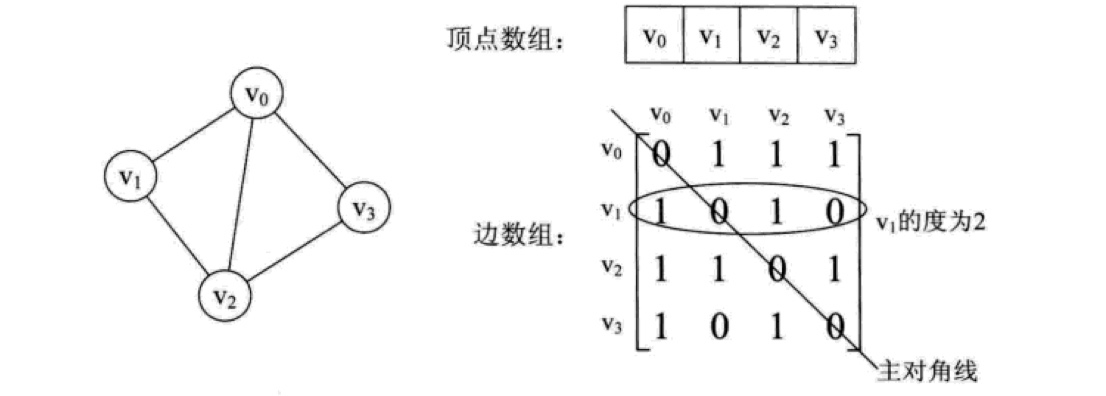
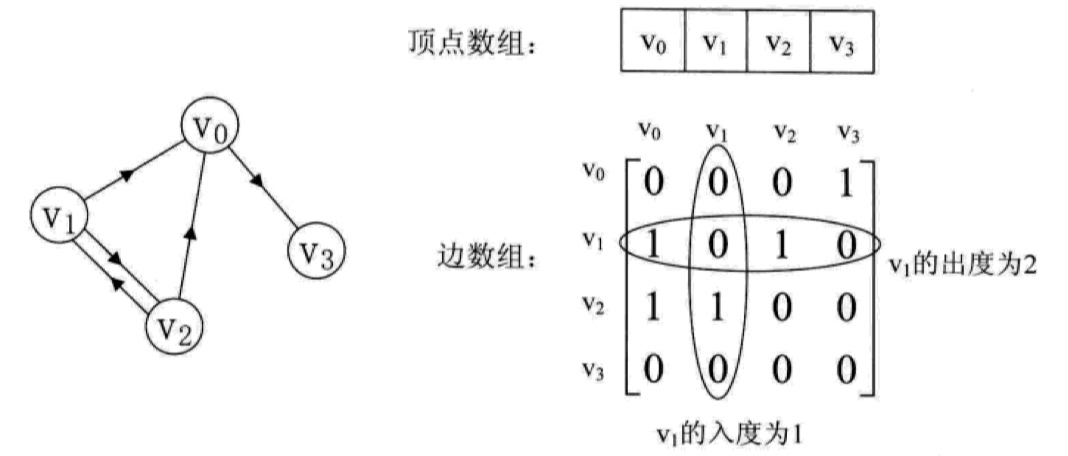
邻接矩阵

对于有 $n$ 个顶点的图而言，时间复杂度是 $O(n^2)$，空间复杂度也是如此，而且如果图比较稀疏的话（稀疏图），边数组会存在巨大的空间浪费。但是优点是实现起来非常简单，对于稠密图或者非常简单的图来说，用邻接矩阵是比较方便的。

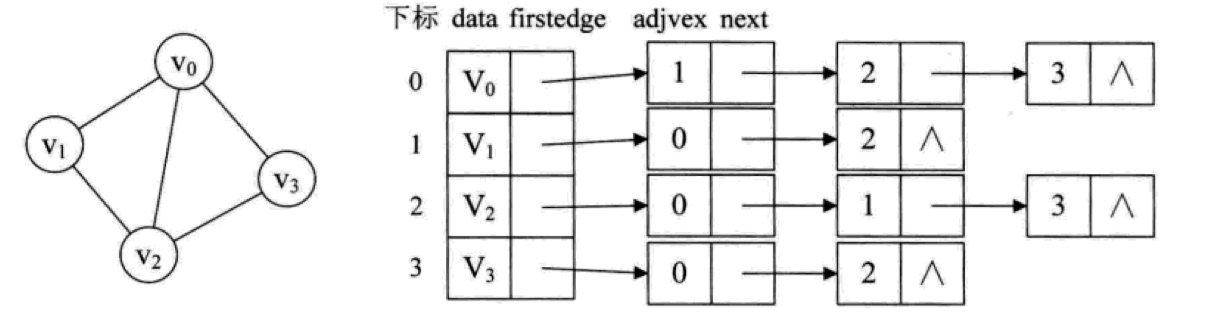
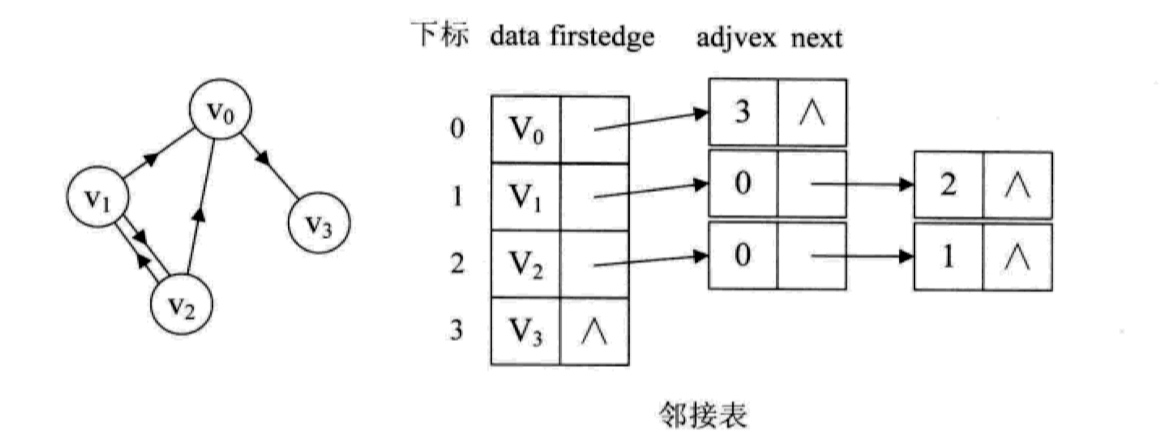
邻接表

邻接表的构建时间复杂度要比邻接矩阵好，对于一个有 $n$ 个顶点和 $m$ 条边的图而言，时间复杂度是 $O(n+m)$，而且不存在任何空间的浪费，比较高效，可用于存储任何图。

二、树与图的深度优先遍历的运用

树的重心

题目描述：
给定一颗树，树中包含 $n$ 个结点（编号 $1\sim n$）和 $n-1$ 条无向边。

请你找到树的重心，并输出将重心删除后，剩余各个连通块中点数的最大值。

重心定义：重心是指树中的一个结点，如果将这个点删除后，剩余各个连通块中点数的最大值最小，那么这个节点被称为树的重心。

输入格式：
第一行包含整数 $n$，表示树的结点数。接下来 $n-1$ 行，每行包含两个整数 $a$ 和 $b$，表示点 $a$ 和点 $b$ 之间存在一条边。

输出格式：
输出一个整数 $m$，表示将重心删除后，剩余各个连通块中点数的最大值。

数据范围：
$1\le n\le 10^5$

输入样例：

9
1 2
1 7
1 4
2 8
2 5
4 3
3 9
4 6

输出样例：

4

题意分析

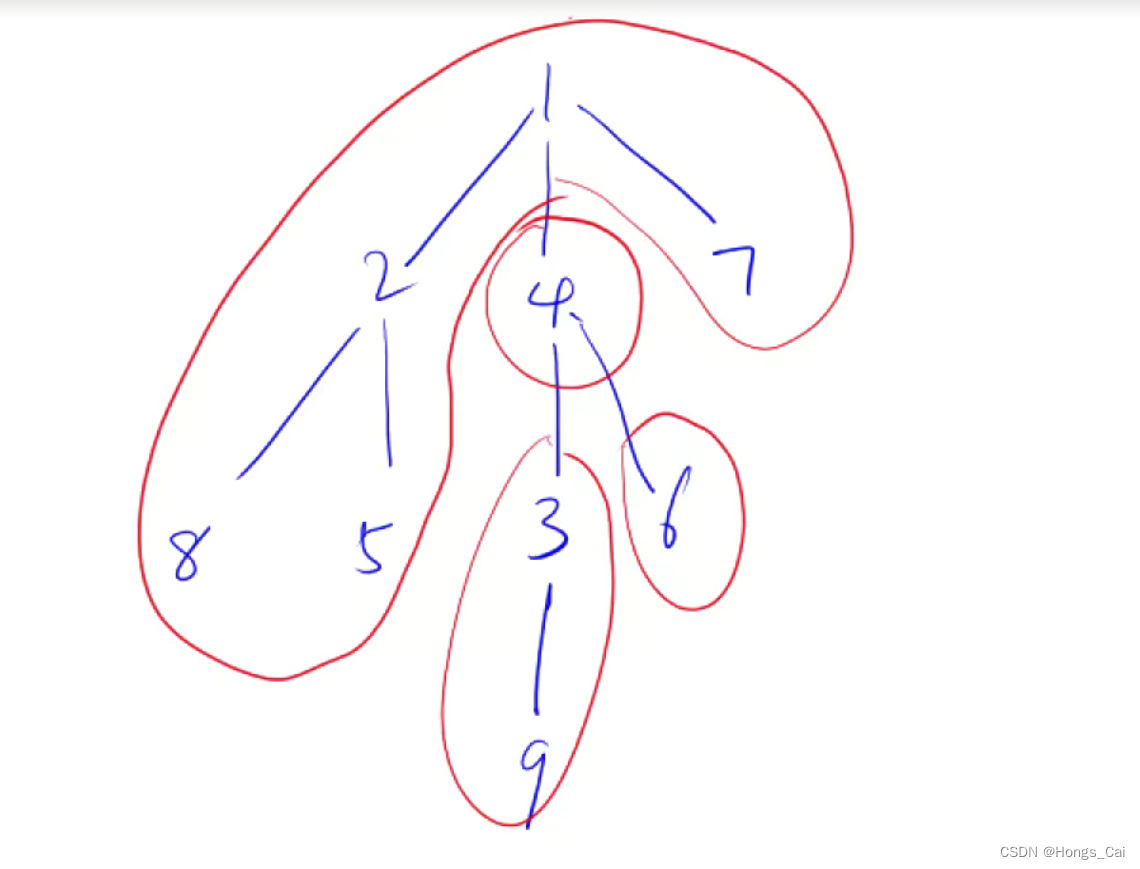
重心是指树中的一个结点，如果将这个点删除后，剩余各个连通块中点数的最大值最小，那么这个节点被称为树的重心。

如下图，4结点删除后个连通块中点数的最大值为5。

代码实现

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>

using namespace std;

const int N = 1e5 + 10, M = N * 2;
int h[N], e[M], ne[M], idx, n, ans = 0x3f3f3f3f;
bool st[N];

void add(int a, int b)
{
	e[idx] = b;
	ne[idx] = h[a];
	h[a] = idx++;
}
int dfs(int u)
{
	st[u] = true;

	int sum = 0, size = 0;

	for (int i = h[u]; i != -1; i = ne[i])
	{
		int j = e[i];
		if (!st[j])
		{
			int s = dfs(j);
			size = max(size, s);
			sum += s;
		}
	}
	size = max(size, n - size - 1);
	ans = min(ans, size);
	return sum + 1;
}
int main()
{
	cin.tie(0);
	ios::sync_with_stdio(false);
	memset(h, -1, sizeof h);
	cin >> n;
	for (int i = 1; i <= n - 1; ++i)
	{
		int a, b;
		cin >> a >> b;
		add(a, b), add(b, a);
	}
	dfs(1);
	cout << ans << endl;
	return 0;
}

三、树与图的广度优先遍历的运用

图中点的层次

题目描述：
给定一个 $n$ 个点 $m$ 条边的有向图，图中可能存在重边和自环。

所有边的长度都是 $1$，点的编号为 $1\sim n$。

请你求出 $1$ 号点到 $n$ 号点的最短距离，如果从 $1$ 号点无法走到 $n$ 号点，输出 $-1$。

输入格式：
第一行包含两个整数 $n$ 和 $m$。

接下来 $m$ 行，每行包含两个整数 $a$ 和 $b$，表示存在一条从 $a$ 走到 $b$ 的长度为 $1$ 的边。

输出格式：
输出一个整数，表示 $1$ 号点到 $n$ 号点的最短距离。

数据范围：
$1\le n,m\le 10^5$

输入样例：

4 5
1 2
2 3
3 4
1 3
1 4

输出样例：

1

题意分析

1. 本题是图的存储 + BFS的结合。

2. 图的存储结构使用的是邻接表。

3. 图的权值是 1 的时候，重边和环不用考虑。

4. 所有长度都是 1，表示可以用 bfs 来求最短路，否则应该用 Dijkstra 等算法来求图中的最短路径。

5. bfs需要记录的是出发点到当前点的距离，就是d数组，每次d要增加1。

6. 注意数组的初始化：
   (1) memset(h,-1,sizeof h); // 数组的整体初始化为-1，这是链表结束循环的边界，缺少会 TLE(Time Limit Exceeded)。
   (2) memset(d,-1,sizeof d); // 表示没有走过。

代码实现

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<queue>

using namespace std;
const int N = 1e5 + 10;
int h[N], e[N * 2], ne[N * 2], d[N], n, m, idx;

void add(int a, int b)
{
	e[idx] = b;
	ne[idx] = h[a];
	h[a] = idx++;
}
int bfs()
{
	queue<int> q;
	q.push(1);
	d[1] = 0;
	while (q.size())
	{
		auto t = q.front();
		q.pop();
		for (int i = h[t]; i != -1; i = ne[i])
		{
			int j = e[i];
			if (d[j] == -1)
			{
				d[j] = d[t] + 1;
				q.push(j);
			}
		}
	}
	return d[n];
}
int main()
{
	cin.tie(0);
	ios::sync_with_stdio(false);
	memset(h, -1, sizeof h);
	memset(d, -1, sizeof d);
	cin >> n >> m;
	for (int i = 1; i <= m; ++i)
	{
		int a, b;
		cin >> a >> b;
		add(a, b);
	}
	cout << bfs() << endl;
	return 0;
}