从 S4 到 S6 的转换过程解释
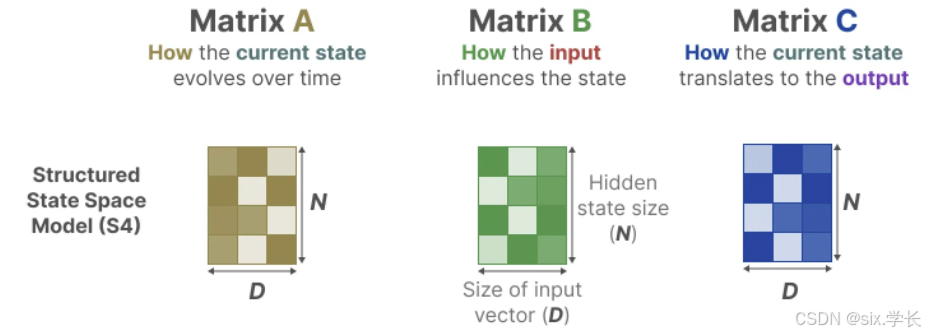
这张图详细说明了从 S4 模型到 S6 模型的转换过程中,参数矩阵 A \mathbf{A} A、 B \mathbf{B} B、 C \mathbf{C} C以及步长 Δ \Delta Δ形状的变化。我们将通过具体的数据举例,解释这些参数如何应用于模型中。
状态空间模型 S4
在 S4 模型中,参数矩阵的形状如下:
- 矩阵
A
\mathbf{A}
A:
(
D
,
N
)
(D, N)
(D,N)
- D D D是输入向量的维度(如颜色通道数 RGB)。
- N N N是隐藏状态维度。 - 矩阵
B
\mathbf{B}
B:
(
D
,
N
)
(D, N)
(D,N)
- 表示输入向量如何影响当前状态。
- 矩阵
C
\mathbf{C}
C:
(
N
,
D
)
(N, D)
(N,D)
- 表示当前状态如何转换为输出。
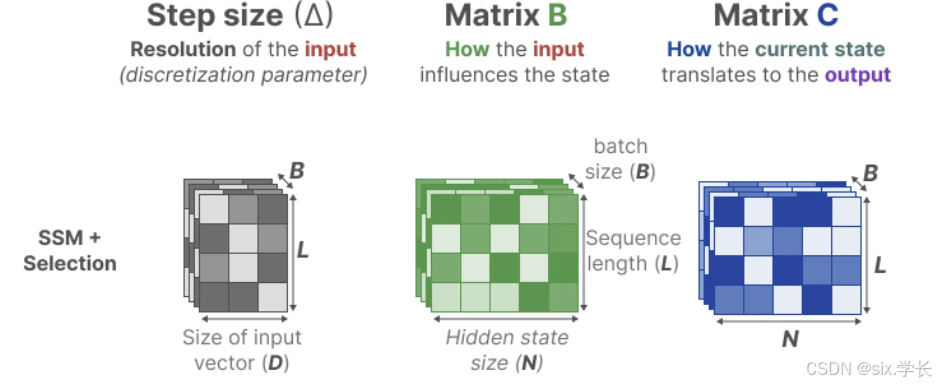
状态空间模型 S6
在 S6 模型中,参数矩阵的形状变为:
- 矩阵
A
\mathbf{A}
A:
(
D
,
N
)
(D, N)
(D,N)
- 保持不变,表示当前状态如何随时间演变。
- 矩阵
B
\mathbf{B}
B:
(
B
,
L
,
N
)
(B, L, N)
(B,L,N)
- 每个批次和序列位置都有一个独特的 B \mathbf{B} B矩阵。
- 矩阵
C
\mathbf{C}
C:
(
B
,
L
,
N
)
(B, L, N)
(B,L,N)
- 每个批次和序列位置都有一个独特的 C \mathbf{C} C矩阵。
- 步长
Δ
\Delta
Δ:
(
B
,
L
,
D
)
(B, L, D)
(B,L,D)
- 每个位置的步长 Δ \Delta Δ都不同,允许对输入序列中的每个位置进行独特的离散化处理。
具体示例
假设我们有以下参数:
- 批量大小 B = 2 B = 2 B=2
- 序列长度 L = 4 L = 4 L=4
- 输入维度 D = 3 D = 3 D=3
- 隐藏状态维度 N = 2 N = 2 N=2
输入矩阵 X \mathbf{X} X
X = ( ( 1 2 3 4 5 6 7 8 9 10 11 12 ) , ( 13 14 15 16 17 18 19 20 21 22 23 24 ) ) \mathbf{X} = \begin{pmatrix} \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\ 10 & 11 & 12 \end{pmatrix}, \begin{pmatrix} 13 & 14 & 15 \\ 16 & 17 & 18 \\ 19 & 20 & 21 \\ 22 & 23 & 24 \end{pmatrix} \end{pmatrix} X= 147102581136912 , 131619221417202315182124
矩阵 A \mathbf{A} A
A = ( 0.5 0.1 0.2 0.3 0.4 0.4 ) \mathbf{A} = \begin{pmatrix} 0.5 & 0.1 \\ 0.2 & 0.3 \\ 0.4 & 0.4 \end{pmatrix} A= 0.50.20.40.10.30.4
矩阵 B \mathbf{B} B在 S4 中
B S 4 = ( 0.7 0.8 0.9 1.0 1.1 1.2 ) \mathbf{B}_{S4} = \begin{pmatrix} 0.7 & 0.8 \\ 0.9 & 1.0 \\ 1.1 & 1.2 \end{pmatrix} BS4= 0.70.91.10.81.01.2
矩阵 B \mathbf{B} B在 S6 中
B S 6 = ( ( 0.7 0.8 0.9 1.0 1.1 1.2 1.3 1.4 ) , ( 1.5 1.6 1.7 1.8 1.9 2.0 2.1 2.2 ) ) \mathbf{B}_{S6} = \begin{pmatrix} \begin{pmatrix} 0.7 & 0.8 \\ 0.9 & 1.0 \\ 1.1 & 1.2 \\ 1.3 & 1.4 \end{pmatrix}, \begin{pmatrix} 1.5 & 1.6 \\ 1.7 & 1.8 \\ 1.9 & 2.0 \\ 2.1 & 2.2 \end{pmatrix} \end{pmatrix} BS6= 0.70.91.11.30.81.01.21.4 , 1.51.71.92.11.61.82.02.2
矩阵 C \mathbf{C} C在 S4 中
C S 4 = ( 1.3 1.4 1.5 1.6 1.7 1.8 ) \mathbf{C}_{S4} = \begin{pmatrix} 1.3 & 1.4 \\ 1.5 & 1.6 \\ 1.7 & 1.8 \end{pmatrix} CS4= 1.31.51.71.41.61.8
矩阵 C \mathbf{C} C在 S6 中
C S 6 = ( ( 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 ) , ( 2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 ) ) \mathbf{C}_{S6} = \begin{pmatrix} \begin{pmatrix} 1.3 & 1.4 \\ 1.5 & 1.6 \\ 1.7 & 1.8 \\ 1.9 & 2.0 \end{pmatrix}, \begin{pmatrix} 2.1 & 2.2 \\ 2.3 & 2.4 \\ 2.5 & 2.6 \\ 2.7 & 2.8 \end{pmatrix} \end{pmatrix} CS6= 1.31.51.71.91.41.61.82.0 , 2.12.32.52.72.22.42.62.8
步长 Δ \Delta Δ在 S6 中
Δ S 6 = ( ( 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 ) , ( 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 2.1 2.2 2.3 2.4 ) ) \Delta_{S6} = \begin{pmatrix} \begin{pmatrix} 0.1 & 0.2 & 0.3 \\ 0.4 & 0.5 & 0.6 \\ 0.7 & 0.8 & 0.9 \\ 1.0 & 1.1 & 1.2 \end{pmatrix}, \begin{pmatrix} 1.3 & 1.4 & 1.5 \\ 1.6 & 1.7 & 1.8 \\ 1.9 & 2.0 & 2.1 \\ 2.2 & 2.3 & 2.4 \end{pmatrix} \end{pmatrix} ΔS6= 0.10.40.71.00.20.50.81.10.30.60.91.2 , 1.31.61.92.21.41.72.02.31.51.82.12.4
处理流程示例
初始化状态 h [ 0 ] \mathbf{h}[0] h[0]
假设初始状态为零向量:
h
[
0
]
=
(
0
0
)
\mathbf{h}[0] = \begin{pmatrix} 0 \\ 0 \end{pmatrix}
h[0]=(00)
计算第一个时间步的状态更新(S4)
h
[
1
]
=
A
h
[
0
]
+
B
S
4
x
[
0
]
=
(
0.5
0.1
0.2
0.3
0.4
0.4
)
(
0
0
)
+
(
0.7
0.8
0.9
1.0
1.1
1.2
)
(
1
2
3
)
\mathbf{h}[1] = \mathbf{A} \mathbf{h}[0] + \mathbf{B}_{S4} \mathbf{x}[0] = \begin{pmatrix} 0.5 & 0.1 \\ 0.2 & 0.3 \\ 0.4 & 0.4 \end{pmatrix} \begin{pmatrix} 0 \\ 0 \end{pmatrix} + \begin{pmatrix} 0.7 & 0.8 \\ 0.9 & 1.0 \\ 1.1 & 1.2 \end{pmatrix} \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}
h[1]=Ah[0]+BS4x[0]=
0.50.20.40.10.30.4
(00)+
0.70.91.10.81.01.2
123
=
(
0.7
×
1
+
0.8
×
2
+
1.1
×
3
0.9
×
1
+
1.0
×
2
+
1.2
×
3
1.1
×
1
+
1.2
×
2
+
1.3
×
3
)
=
(
5.7
8.3
11.1
)
= \begin{pmatrix} 0.7 \times 1 + 0.8 \times 2 + 1.1 \times 3 \\ 0.9 \times 1 + 1.0 \times 2 + 1.2 \times 3 \\ 1.1 \times 1 + 1.2 \times 2 + 1.3 \times 3 \end{pmatrix} = \begin{pmatrix} 5.7 \\ 8.3 \\ 11.1 \end{pmatrix}
=
0.7×1+0.8×2+1.1×30.9×1+1.0×2+1.2×31.1×1+1.2×2+1.3×3
=
5.78.311.1
计算第一个时间步的状态更新(S6)
在 S6 中,状态更新公式类似,但使用的是每个位置独特的
B
\mathbf{B}
B矩阵和
Δ
\Delta
Δ:
h
[
1
]
=
A
h
[
0
]
+
B
S
6
x
[
0
]
=
(
0.5
0.1
0.2
0.3
0.4
0.4
)
(
0
0
)
+
(
0.7
0.8
0.9
1.0
1.1
1.2
)
(
1
2
3
)
\mathbf{h}[1] = \mathbf{A} \mathbf{h}[0] + \mathbf{B}_{S6} \mathbf{x}[0] = \begin{pmatrix} 0.5 & 0.1 \\ 0.2 & 0.3 \\ 0.4 & 0.4 \end{pmatrix} \begin{pmatrix} 0 \\ 0 \end{pmatrix} + \begin{pmatrix} 0.7 & 0.8 \\ 0.9 & 1.0 \\ 1.1 & 1.2 \end{pmatrix} \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}
h[1]=Ah[0]+BS6x[0]=
0.50.20.40.10.30.4
(00)+
0.70.91.10.81.01.2
123
=
(
5.7
8.3
11.1
)
= \begin{pmatrix} 5.7 \\ 8.3 \\ 11.1 \end{pmatrix}
=
5.78.311.1
输出计算(S4)
y
[
1
]
=
C
S
4
h
[
1
]
=
(
1.3
1.4
1.5
1.6
1.7
1.8
)
(
5.7
8.3
)
\mathbf{y}[1] = \mathbf{C}_{S4} \mathbf{h}[1] = \begin{pmatrix} 1.3 & 1.4 \\ 1.5 & 1.6 \\ 1.7 & 1.8 \end{pmatrix} \begin{pmatrix} 5.7 \\ 8.3 \end{pmatrix}
y[1]=CS4h[1]=
1.31.51.71.41.61.8
(5.78.3)
=
(
1.3
×
5.7
+
1.4
×
8.3
1.5
×
5.7
+
1.6
×
8.3
1.7
×
5.7
+
1.8
×
8.3
)
=
(
18.91
21.51
24.11
)
= \begin{pmatrix} 1.3 \times 5.7 + 1.4 \times 8.3 \\ 1.5 \times 5.7 + 1.6 \times 8.3 \\ 1.7 \times 5 .7 + 1.8 \times 8.3 \end{pmatrix} = \begin{pmatrix} 18.91 \\ 21.51 \\ 24.11 \end{pmatrix}
=
1.3×5.7+1.4×8.31.5×5.7+1.6×8.31.7×5.7+1.8×8.3
=
18.9121.5124.11
输出计算(S6)
y
[
1
]
=
C
S
6
h
[
1
]
=
(
1.3
1.4
1.5
1.6
1.7
1.8
)
(
5.7
8.3
)
\mathbf{y}[1] = \mathbf{C}_{S6} \mathbf{h}[1] = \begin{pmatrix} 1.3 & 1.4 \\ 1.5 & 1.6 \\ 1.7 & 1.8 \end{pmatrix} \begin{pmatrix} 5.7 \\ 8.3 \end{pmatrix}
y[1]=CS6h[1]=
1.31.51.71.41.61.8
(5.78.3)
=
(
18.91
21.51
24.11
)
= \begin{pmatrix} 18.91 \\ 21.51 \\ 24.11 \end{pmatrix}
=
18.9121.5124.11
总结
通过这个具体的例子,我们展示了从 S4 模型到 S6 模型的转换过程。S6 模型通过为每个批次和序列位置提供独特的 B \mathbf{B} B、 C \mathbf{C} C和 Δ \Delta Δ参数,从而允许更加灵活和精细的处理。这种方法能够更好地适应输入数据的变化,提高模型的性能和表达能力。