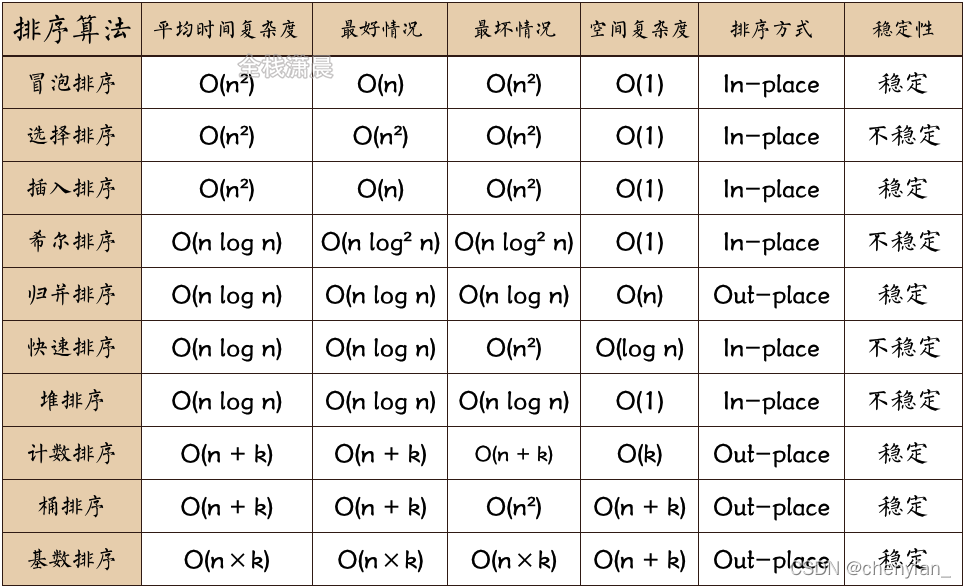
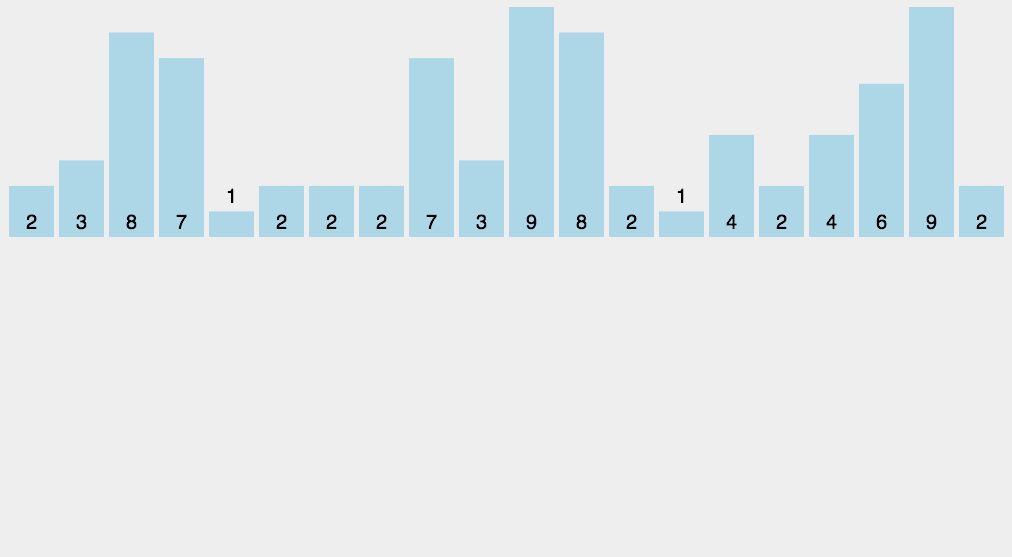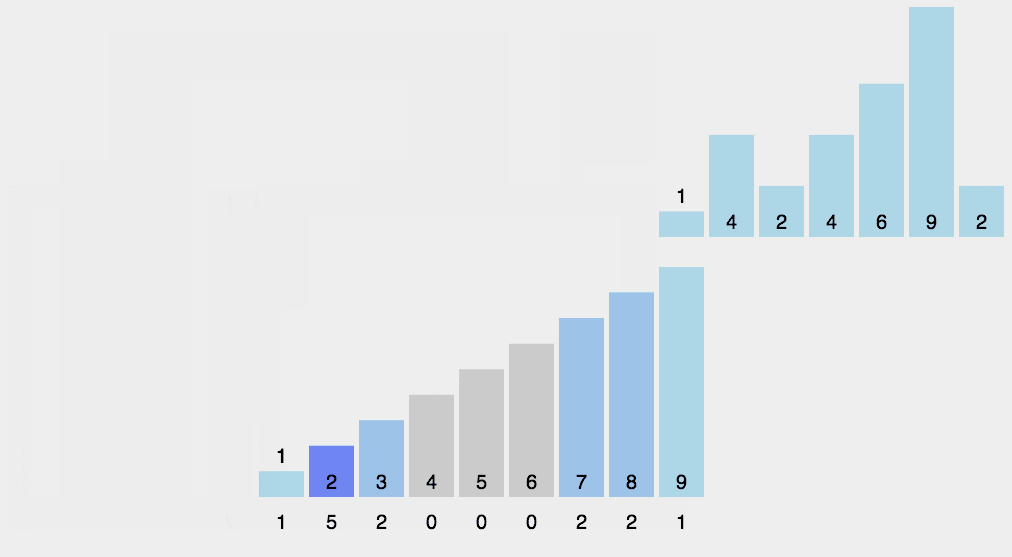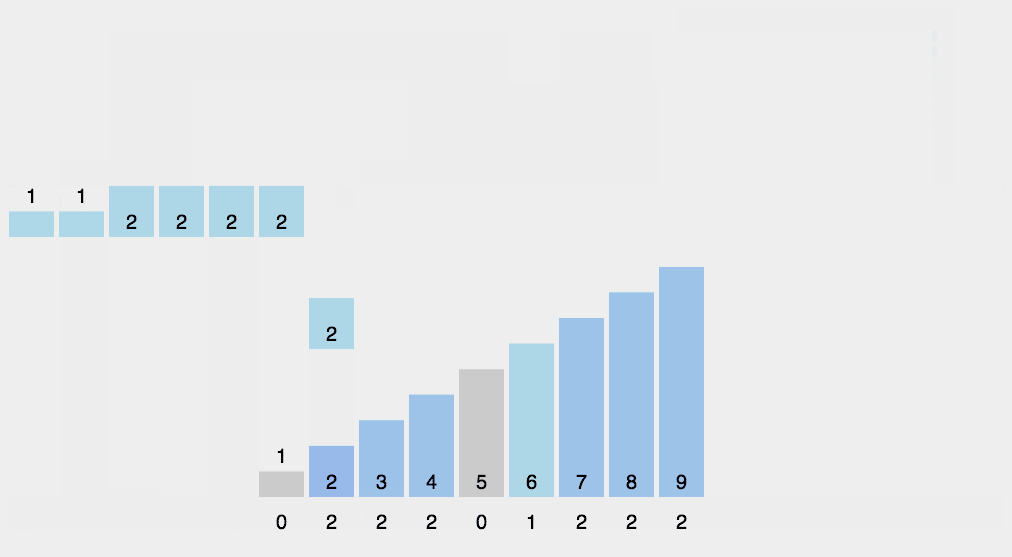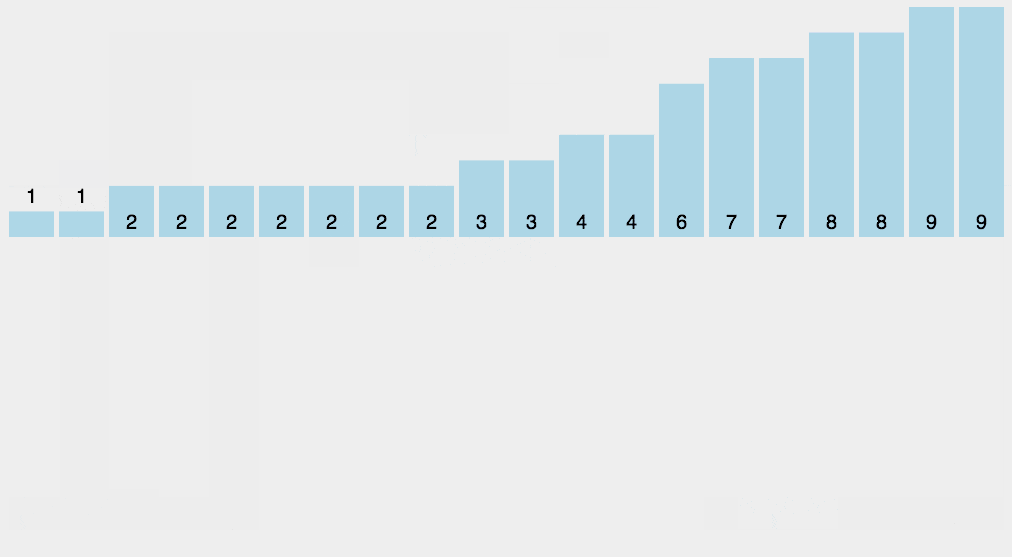排序算法
排序算法(英语:Sorting algorithm)是一种将一组特定的数据按某种顺序进行排列的算法。排序算法多种多样,性质也大多不同。
(一)稳定性:
稳定性是指相等的元素经过排序之后相对顺序是否发生了改变。
稳定的排序算法会让原本有相等键值的纪录维持相对次序。
-
稳定排序:基数排序、计数排序、插入排序、冒泡排序、归并排序、桶排序。
-
不稳定排序:选择排序、希尔排序、堆排序、快速排序。
(二)复杂度:
基于比较的排序算法的时间复杂度下限是
O
(
n
l
o
g
n
)
O(n logn)
O(nlogn) 的。
当然也有不是
O
(
n
l
o
g
n
)
O(n logn)
O(nlogn) 的。例如,计数排序 的时间复杂度是
O
(
n
+
w
)
O(n+w)
O(n+w) ,其中
w
w
w 代表输入数据的值域大小。
(三)存储器:
- 内部排序: 待排序记录存放在计算机随机存储器中进行的排序过程;
- 外部排序: 待排序记录的数量很大,以致内存一次不能容纳全部记录,在排序过程中尚需对外存进行访问的排序过程。
1. 选择排序(Selection sort)
- 工作原理:每次找出第
i
i
i 小的元素(也就是
A
A
Ai…n 中最小的元素),然后将这个元素与数组第
i
i
i 个位置上的元素交换。
- 不稳定性:由于 swap(交换两个元素)操作的存在,选择排序是一种不稳定的排序算法。
- 时间复杂度:最优时间复杂度、平均时间复杂度和最坏时间复杂度均为 O ( n 2 ) O(n^2) O(n2)
#include <iostream>
using namespace std;
void sort(int* nums, int n){ // 数组指针 数组大小
for(int i = 0; i < n; ++i){
int min_index = i;
for(int j = i+1; j < n; ++j){
if(nums[j] < nums[min_index]) min_index = j;
}
swap(nums[i], nums[min_index]);
}
}
int main(){
int nums[] = {0,2,6,1,5,4,3,7};
sort(nums, 8);
for(int num : nums){
cout << num << endl;
}
return 0;
}
2. 冒泡排序(Bubble sort)
在算法的执行过程中,较小的元素像是气泡般慢慢「浮」到数列的顶端,故叫做冒泡排序。
- 工作原理:
每次检查相邻两个元素,如果前面的元素与后面的元素满足给定的排序条件,就将相邻两个元素交换。当没有相邻的元素需要交换时,排序就完成了。
经过 i i i 次扫描后,数列的末尾 i i i 项必然是最大的 i i i 项,因此冒泡排序最多需要扫描 n − 1 n-1 n−1遍数组就能完成排序。 - 稳定性:
冒泡排序是稳定排序算法。 - 时间复杂度:
在序列完全有序时,冒泡排序只需遍历一遍数组,不用执行任何交换操作,时间复杂度为 O ( n ) O(n) O(n)。
在最坏情况下,冒泡排序要执行 ( n − 1 ) n / 2 (n-1)n/2 (n−1)n/2 次交换操作,时间复杂度为 O ( n 2 ) O(n^2) O(n2)。
冒泡排序的平均时间复杂度为 O ( n 2 ) O(n^2) O(n2)。
#include <iostream>
using namespace std;
void sort(int* nums, int n){ // 数组指针 数组大小
for(int j = 0; j < n; ++j){ // 大循环遍历(最多n-1次)
bool flag = true;
for(int i = 1; i < n; ++i){ // i < n- j
if(nums[i] < nums[i-1]){ // 相邻两个元素逐一比较
swap(nums[i], nums[i-1]);
flag = false;
}
}
if(flag == true) break; // true 为当前遍历未发生交换
}
}
int main(){
int nums[] = {0,2,6,1,5,4,3,7};
sort(nums, 8);
for(int num : nums){
cout << num << endl;
}
return 0;
}
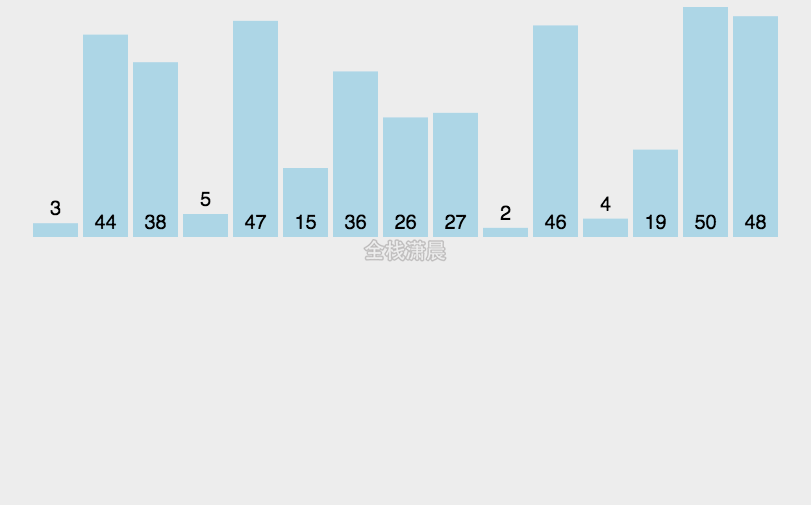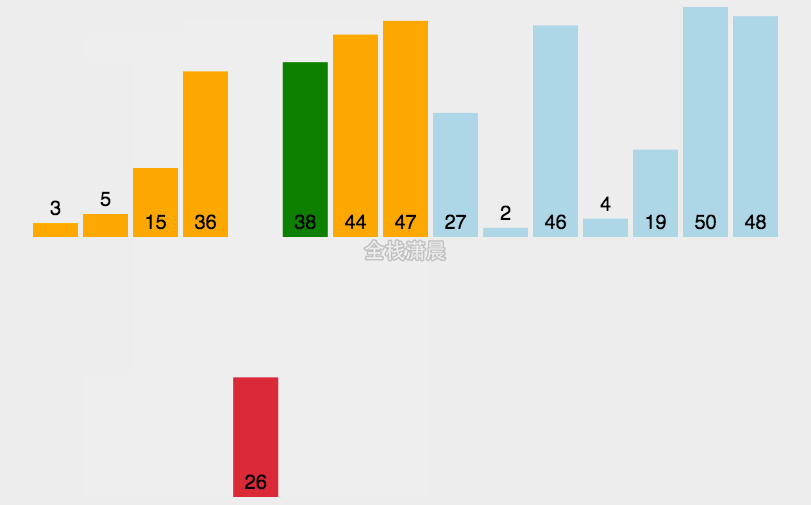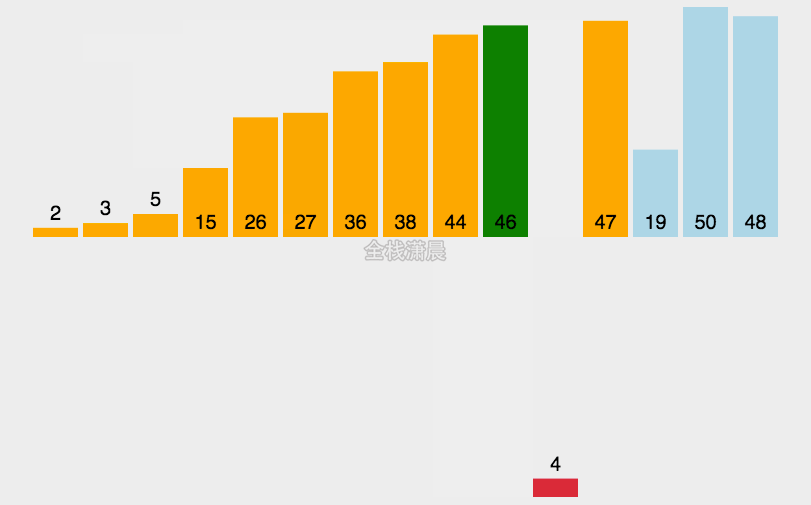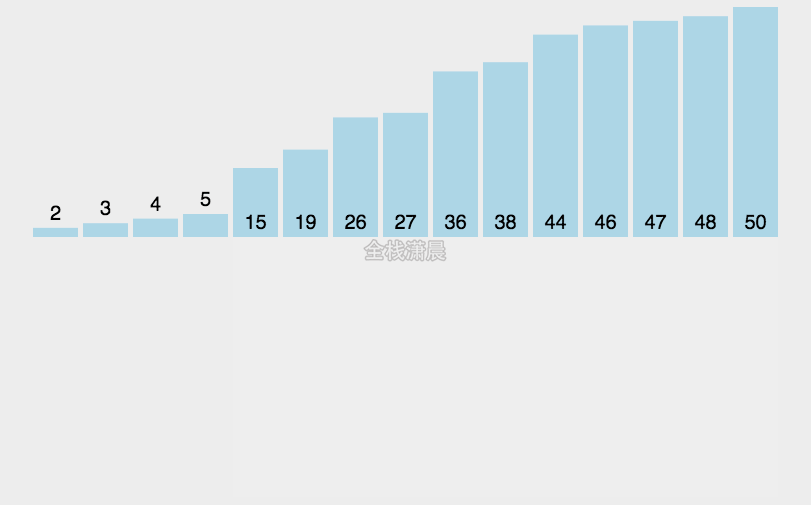
3. 插入排序(Insertion sort)
- 工作原理:
将待排列元素划分为“已排序”和“未排序”两部分,每次从“未排序的”元素中选择一个插入到“已排序的”元素中的正确位置。
- 稳定性:
插入排序是稳定的排序算法。 - 时间复杂度:
插入排序的最优时间复杂度为 O ( n ) O(n) O(n),在数列几乎有序时效率很高。
插入排序的最坏时间复杂度和平均时间复杂度都为 O ( n 2 ) O(n^2) O(n2)。
// insertion sort
#include <iostream>
using namespace std;
void sort(int* nums, int n){ // 数组指针 数组大小
for(int i = 1; i < n; ++i){
int curr = nums[i]; // 当前需要插入的元素
while(nums[i-1] > curr && i > 0){ // 从后往前遍历已排序部分
nums[i] = nums[i-1]; // 更大元素后移
--i;
}
nums[i] = curr; // 插入正确位置
}
}
int main(){
int nums[] = {7,6,5,4,1,2,3,0};
int ans[] = {0,1,2,3,4,5,6,7};
int n = 8;
sort(nums, n); // 排序
bool result = true;
for(int i = 0; i < n; ++i){
if(nums[i] != ans[i]) result = false;
cout << nums[i] << endl;
}
cout << "result is: " << result << endl;
return 0;
}
4. 希尔排序(Shell sort)
也称为缩小增量排序法,是 插入排序 的一种改进版本。
- 工作原理 :
(1)将待排序序列分为 若干子序列 (每个子序列的元素在原始数组中 间距step相同 );
(2)对这些子序列进行 插入排序 ;
(3)减小每个子序列中元素之间的间距,重复上述过程直至 间距减少为 1 。 - 不稳定性:
希尔排序是不稳定的排序算法。 - 复杂度:
最优时间复杂度为 O ( n ) O(n) O(n);
平均时间复杂度和最坏时间复杂度与间距序列的选取(就是间距如何减小到 1)有关,
常见的增量值有 N 2 i \frac N{2^i} 2iN,即对序列的长度不断折半作为增量大小。还有 2 k − 1 2^k-1 2k−1。
比如「间距每次除以 3」的希尔排序的时间复杂度是 O ( n 3 / 2 ) O(n^{3/2}) O(n3/2)。已知最好的最坏时间复杂度为 O ( n l o g 2 n ) O(nlog^2n) O(nlog2n) 。
空间复杂度为 O ( 1 ) O(1) O(1)。
希尔排序属于原地排序算法,不需要申请额外的存储空间。它是在插入排序的基础上进行了改进,实际就是除了最后的插入排序外,对多个子分组也执行了排序。所以看到该算法的第一印象就是,它额外做了这么多工作,复杂度应该大于插入排序才对。所以导致希尔排序最坏复杂度低于插入排序的原因就是,通过合理的增量值设置,可以将本来需要多次比较和交换才能调整到正确位置的元素,只需要很少次的比较和交换就可完成。
#include <iostream>
#include <vector>
using namespace std;
void shellSort(vector<int>& nums){
int n = nums.size();
for(int step = n / 2; step > 0; step /= 2){ // 间距以两倍缩减到 1
for(int index = 0; index < step; ++index){ // 遍历相同间距下的不同组,进行插入排序
// 该内层循环为插入排序
for(int i = index + step; i < n; i += step){ // 从每组的第二个元素开始step递增,分成排序和未排序部分,第一个元素为index
int curr = nums[i]; // i = index + step 属于待排序元素
while (nums[i - step] > curr && i > index)
{
nums[i] = nums[i - step];
i -= step;
}
nums[i] = curr;
}
}
}
}
int main(){
vector<int> nums = {6,5 ,4 ,8, 9 ,11, 55, 10, 0, 3, 2, 1, 7};
shellSort(nums);
for(int i = 0; i < nums.size(); i++){
cout << nums[i] << " ";
}
return 0;
}
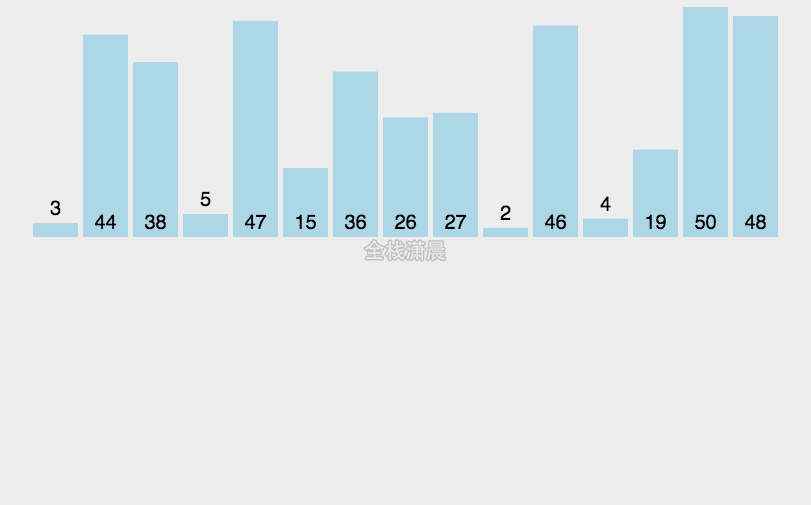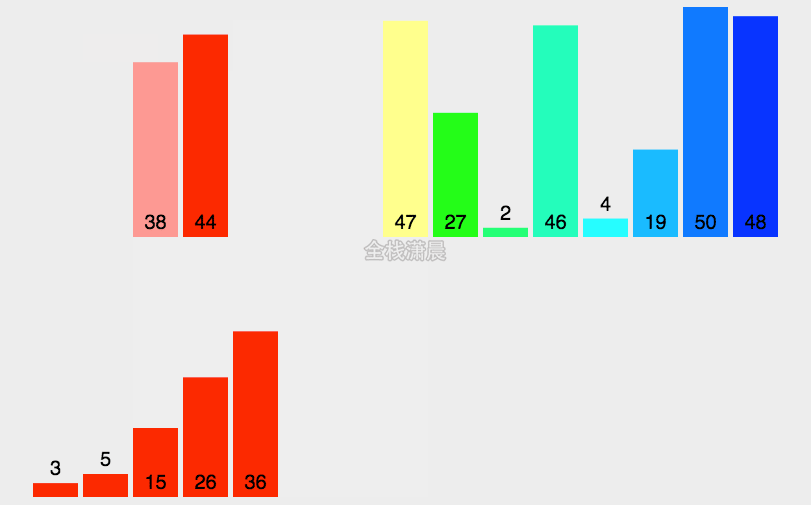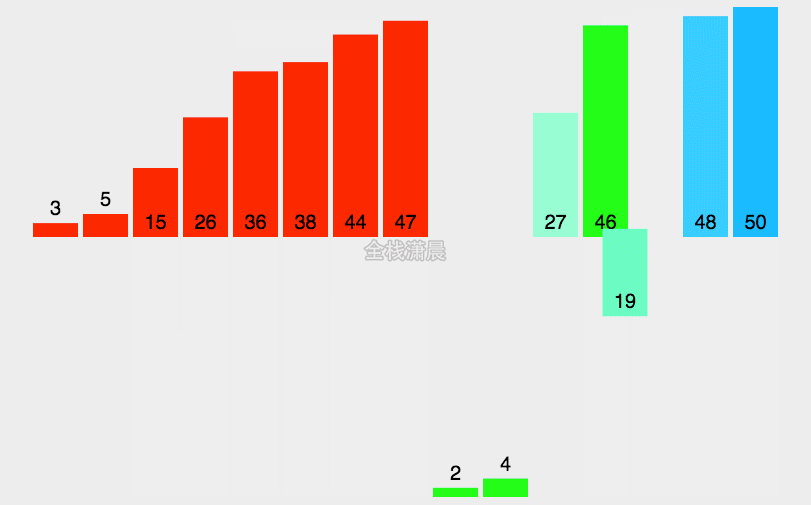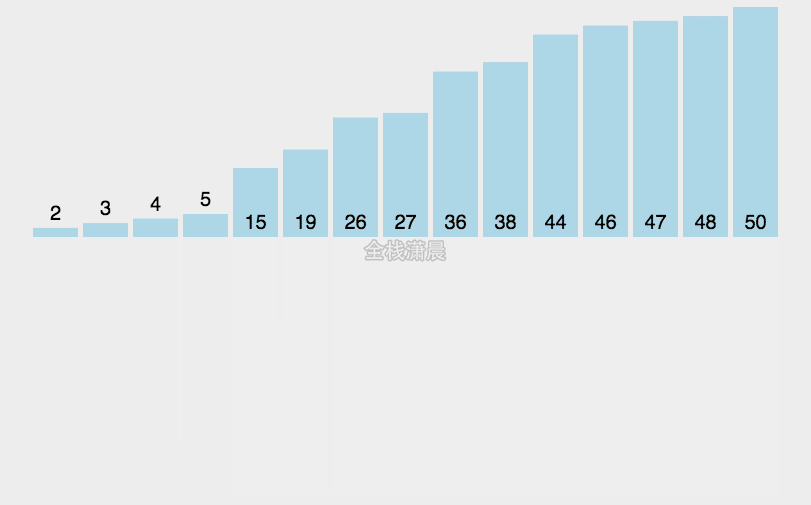
5. 归并排序(Merge sort)
归并排序是通过分治的方式,将待排序集合拆分为多个子集合,对子集合排序后,合并子集合成为较大的子集合,不断合并最终完成整个集合的排序。
以下所讲归并都是指二路归并:
之前的冒泡、选择和插入排序都是维持一个待排序集合和一个已排序集合,在每次的迭代过程中从待排序集合中移动一个元素到已排序集合中,通过不断的迭代来完成排序,所以需要进行的迭代次数一般都是 O ( N ) O(N) O(N) 级别。
而归并排序则是每轮迭代消除半数的待排序子集合,所以需要进行的迭代次数为 O ( l o g 2 N ) O(log_2N) O(log2N) 级别。
步骤为:
(1)将数列划分为两部分;
(2)递归地分别对两个子序列进行归并排序;
(3)合并两个有序子序列。
性质:
归并排序是一种稳定的排序算法。
归并排序的最优时间复杂度、平均时间复杂度和最坏时间复杂度均为
O
(
n
l
o
g
n
)
O(nlogn)
O(nlogn) 。
归并排序的空间复杂度为
O
(
n
)
O(n)
O(n) 。
归并排序适用于数据量大,并且对稳定性有要求的场景。
代码中采用递归的思路进行划分-排序-合并,
在排序前先创建备用数组sorted,避免递归时重复创建增加消耗。
#include <iostream>
#include <vector>
using namespace std;
int reversePairNum = 0; // 逆序对,就是对于一个数组 ,满足 nums[i] > nums[j] 且 i < j 的数对 (i, j)。
void mergeSort(vector<int> &nums, vector<int> &sorted, int start, int end){
if(start >= end) return; // 只有一个元素
int mid = (start + end) >> 1; // 分割数组
mergeSort(nums, sorted, start, mid); // 排序左半边
mergeSort(nums, sorted, mid+1, end); // 排序右半边
int left = start, right = mid + 1; // 将有序的左右两边数组进行合并
for(int i = start; i <= end; ++i){ // 合并的数组暂存到sorted
if((nums[left] > nums[right] && right <= end) || left > mid){
sorted[i] = nums[right++]; // 比较左右指针的大小,同时不能超过子数组的长度
reversePairNum += mid - left + 1; // 原数组中求逆序对的个数
// 具体来说,算法把靠后的数放到前面了(较小的数放在前面),所以在这个数原来位置之前的、比它大的数都会和它形成逆序对,
// 而这个个数就是还没有合并进去的数的个数,即$mid - left + 1$。
}else{
sorted[i] = nums[left++];
}
// 以上等效于:
// if(left > mid){
// sorted[i] = nums[right++];
// }else if(right > end){
// sorted[i] = nums[left++];
// }else if(nums[left] > nums[right]){
// sorted[i] = nums[right++];
// }else{
// sorted[i] = nums[left++];
// }
}
for(int i = start; i <= end; ++i){ // 复制
nums[i] = sorted[i];
}
}
int main(){
vector<int> nums = {10,9,8,7,6,5,4,3,2,1,0,15,14,13,12,11,-1,-2,-3,-6,-5,-4};
vector<int> sorted(nums.size(), 0); // 先创建备用数组,避免递归时重复创建增加消耗
mergeSort(nums, sorted, 0, nums.size()-1); // 归并排序
for(int i = 0; i < nums.size(); i++){
cout << nums[i] << " ";
}
return 0;
}
- 逆序对
归并排序还可以用来求逆序对的个数。
所谓逆序对,就是对于一个数组 ,满足
n
u
m
s
[
i
]
>
n
u
m
s
[
j
]
nums[i] > nums[j]
nums[i]>nums[j] 且
i
<
j
i < j
i<j 的数对
(
i
,
j
)
(i, j)
(i,j)。
代码实现中 reversePairNum += mid - left + 1; 就是在统计逆序对个数。
具体来说,算法把靠后的数放到前面了(较小的数放在前面),所以在这个数原来位置之前的、比它大的数都会和它形成逆序对,而这个个数就是还没有合并进去的数的个数,即
m
i
d
−
l
e
f
t
+
1
mid - left + 1
mid−left+1。
6. 快速排序(Quick sort)
快速排序,又称分区交换排序(partition-exchange sort),简称快排,是内排序中平均效率最高的排序算法。
快速排序的工作原理是通过 分治 的方式来将一个数组排序。
通过多次比较和交换来实现排序,在一趟排序中把将要排序的数据分成两个独立的部分,对这两部分进行排序使得其中一部分所有数据比另一部分都要小,然后继续递归排序这两部分,最终实现所有数据有序。
快速排序分为三个过程:
(1)首先设置一个分界值,通过该分界值将数据分割成两部分(要求保证相对大小关系);
(2)递归到两个子序列中分别进行快速排序;
(3)不用合并,因为此时数列已经完全有序。
-
稳定性
快速排序是一种不稳定的排序算法。 -
时间复杂度:分区复杂度 O ( n ) O(n) O(n),递归复杂度是 O ( l o g n ) O(logn) O(logn)
快速排序的最优时间复杂度和平均时间复杂度为 O ( n l o g n ) O(nlogn) O(nlogn) ,最坏时间复杂度为 O ( n 2 ) O(n^2) O(n2) 。
最坏情况下,每次所选的分界值是当前序列中的最大或最小元素,这使得每次划分所得的子表中一个为空表,另一子表的长度为原表的长度-1。这样,长度为 n 的数据表的快速排序需要经过 n 趟划分,使得整个排序算法的时间复杂度为 O ( n 2 ) O(n^2) O(n2),可以通过随机选择分界值来避免这种情况。 -
空间复杂度:递归层数 O ( l o g n ) O(logn) O(logn)
#include <iostream>
#include <vector>
using namespace std;
void Qsort(vector<int> &nums, int left, int right){
if(left >= right) return;
int line = nums[left]; // 取首个元素为分界值
int changePos = 0; // changePos记录交换了的元素个数,交换位置为left + changePos
for(int i = left; i <= right; ++i){ // 遍历元素
if(nums[i] < line){ // 当右边元素值出现小于分界值时
++changePos; // 交换位置后移
if(i != left + changePos) swap(nums[i], nums[left + changePos]); // 交换元素
}
}
swap(nums[left], nums[left + changePos]); // 把分界值移动到中间(分界线)位置
Qsort(nums, left, left + changePos - 1); // 递归左边元素
Qsort(nums, left + changePos + 1, right); // 递归右边元素
}
int main(){
vector<int> nums;// = {6,5 ,4 ,8, 9 ,11, 55, 10, 0, 3, 2, 1, 7};
cout << "emter the number of elements: ";
int n;
cin >> n;
cout << "enter the elements: ";
int num;
for(int i = 0; i < n; ++i){
cin >> num;
nums.push_back(num);
}
Qsort(nums, 0, n-1);
for(int i = 0; i < n; i++){
cout << nums[i] << " ";
}
return 0;
}
7. 堆排序(Heapsort)
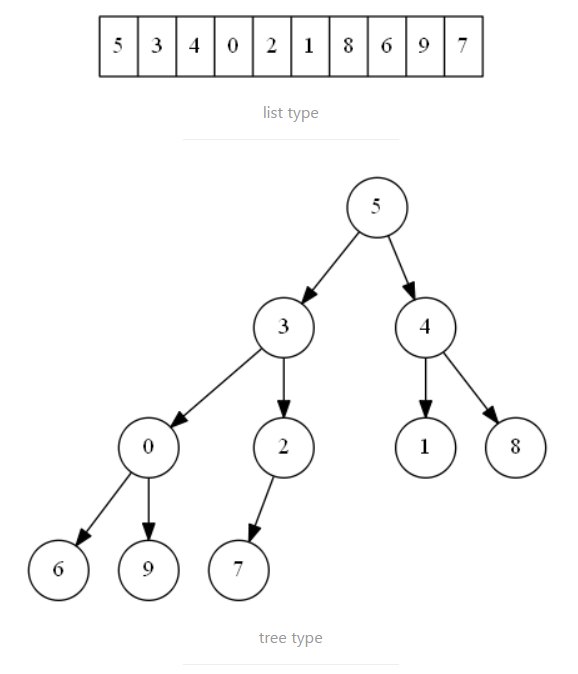
堆描述的是一颗完全二叉树,父节点的值不小于子节点的值则是大根堆,父不大于子则是小根堆。
在对数组进行排序的过程中,并不是真的构建一个二叉树结构,只是将数组中元素下标映射到完全二叉树,利用元素下标来表示父节点和子节点关系。
二叉堆的结构、插入、删除、修改
通过以上两张图可知,堆中父子节点的下标关系为:
– 下标为
i
i
i 的节点,其左子节点下标为
2
∗
i
+
1
2*i+1
2∗i+1
– 下标为
i
i
i 的节点,其右子节点下标为
2
∗
i
+
2
2*i+2
2∗i+2
– 下标为
i
i
i 的节点,其父节点下标为
⌊
i
−
1
2
⌋
(
i
≥
1
)
\lfloor {\frac {i-1} 2} \rfloor(i\ge1)
⌊2i−1⌋(i≥1)
算法步骤:
- 将无序序列构建成一个初始堆,根据升序降序需求选择大顶堆或小顶堆;
- 交换待排序集合中第一个元素和最后一个元素值,即在待排序集合映射出的完全二叉树上,将根节点值和树中最下面一层、最右边的节点值进行替换
- 重新调整结构,使其满足堆定义,标记待排序集合最后一个元素为已排序
- 重复步骤2、3,直到待排序集合只有一个元素
构建初始堆:
首先要清楚数组下标和元素在树结构中位置的关系,然后关键是要找到 最后一个非叶子节点(下标为n/2-1) 开始,逐个进行堆结构的调整,在交换之后,要继续往下检查调整。
不稳定性:
同选择排序一样,由于其中交换位置的操作,所以是不稳定的排序算法。
时间复杂度:
堆排序的最优时间复杂度、平均时间复杂度、最坏时间复杂度均为
O
(
n
l
o
g
n
)
O(nlogn)
O(nlogn)。
空间复杂度:
由于可以在输入数组上建立堆,所以这是一个原地算法
O
(
1
)
O(1)
O(1)。
对于 n n n 个元素的序列,构造堆过程,需要遍历的元素次数为 O ( n ) O(n) O(n),每个元素的调整次数为 O ( l o g 2 n ) O(log_2n) O(log2n),所以构造堆复杂度为 O ( n l o g n ) O(nlogn) O(nlogn) 。迭代替换待排序集合首尾元素的次数为 O ( n ) O(n) O(n),每次替换后调整次数为 O ( l o g 2 n ) O(log_2n) O(log2n),所以迭代操作的复杂度为 O ( n l o g n ) O(nlogn) O(nlogn)。由此可知堆排序的时间复杂度为 O ( n l o g n ) O(nlogn) O(nlogn) ,排序过程属于原地排序,不需要额外的存储空间,所以空间复杂度为 O ( 1 ) O(1) O(1)。
#include <iostream>
#include <vector>
using namespace std;
// 从节点下标root开始向下调整堆结构,最大长度为n
void heapAdjust(vector<int>& nums, int root, int n){
int child = 2 * root + 1;
if(child >= n) return; // 叶子节点,没有左孩子
while(child < n){
if(child + 1 < n && nums[child] < nums[child+1]){
++child; // 存在右孩子且 右>左时,则与右比较
}
if(nums[root] < nums[child]){
swap(nums[root], nums[child]); // 交换
root = child;
child = 2 * root + 1; // 内层向下调整
}else{
break; // 父节点最大,不需要调整了
}
}
}
// 堆排序,先构建初始堆,再逐一交换-调整
void heapSort(vector<int> &nums){
int n = nums.size();
for(int i = n / 2 - 1; i >= 0; --i){ // 从最后一个非叶子节点,外层向上调整
heapAdjust(nums, i, n);
}
for(int i = 0; i < n-1; ++i){
swap(nums[n-1-i], nums[0]); // 交换未排序首位
heapAdjust(nums, 0, n-i-1); // 从根节点开始调整
}
}
int main(){
vector<int> nums = {10,9,8,7,6,5,4,3,2,1,0,15,14,13,12,11,-1,-2,-3,-6,-5,-4};
heapSort(nums);
for(int i = 0; i < nums.size(); i++){
cout << nums[i] << " ";
}
return 0;
}
8. 计数排序(Counting sort)
- 工作原理:
使用一个额外的数组 C C C,其中第 i i i 个元素是待排序数组 A A A 中值等于 i i i 的元素的个数,然后根据数组 C C C 来将 A A A 中的元素排到正确的位置。
- 工作步骤:
1.计算每个数出现的次数;
2.求出每个数出现次数的 前缀和;
3.利用出现次数的前缀和,从右至左计算每个数的排名。 - 稳定性:
计数排序是一种稳定的排序算法。 - 复杂度:
时间复杂度为 O ( n + w ) O(n+w) O(n+w),
空间复杂度为 O ( w ) O(w) O(w),其中 w w w 代表待排序数据的值域大小。 - 局限性:
(1)当数列最大最小值差距 (值域)过大 时,会造成空间浪费,并不适用于计数排序;
(2)当数列元素不是整数时,无法创建对应的统计数组,并不适用于计数排序。
// Counting sort
#include <iostream>
using namespace std;
void sort(int* nums, int n){ // 数组指针 数组大小
int min = nums[0];
int max = nums[0];
for(int i = 1; i < n; ++i){ // 确定数值最大最小值,确定值域大小
if(nums[i] > max) max = nums[i];
if(nums[i] < min) min = nums[i];
}
int w = max - min + 1; // 值域大小
int cnt[w] = {0}; // 统计数组
for(int i = 0; i < n; ++i) ++cnt[nums[i]-min]; // cnt数组统计每个数值出现的次数
int index = 0;
for(int i = 0; i < w; ++i){ // 根据数值个数进行排序
while(cnt[i] > 0){
nums[index] = i + min; // 偏置
--cnt[i];
++index;
}
}
}
int main(){
int nums[] = {0,2,6,1,5,7,4,3,7};
int ans[] = {0,1,2,3,4,5,6,7,7};
int n = 9;
sort(nums, n); // 排序
bool result = true;
for(int i = 0; i < n; ++i){
if(nums[i] != ans[i]) result = false;
cout << nums[i] << endl;
}
cout << "result is: " << result << endl;
return 0;
}
稳定的计数排序过程可见基数排序部分。
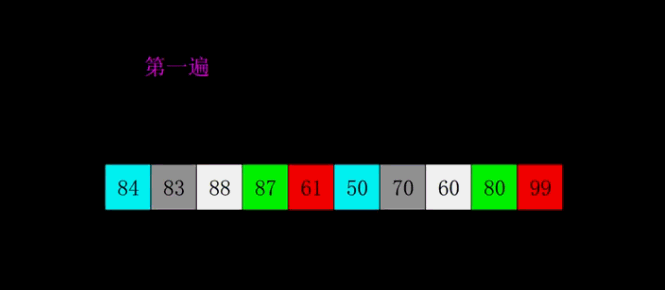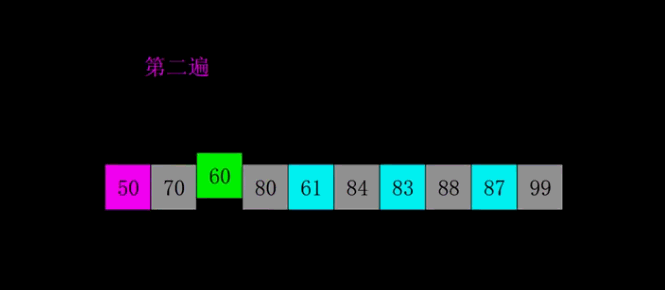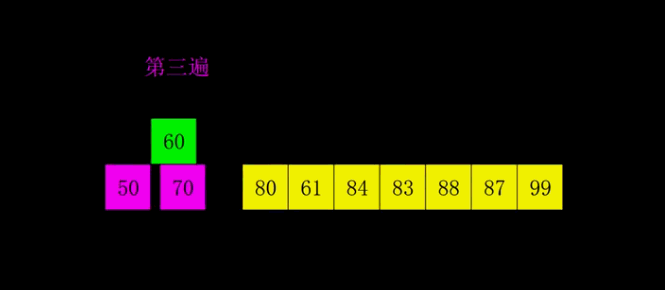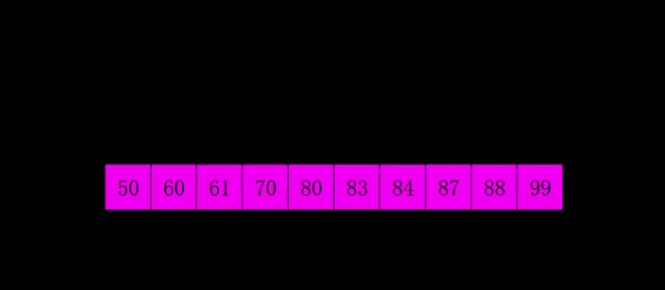
9. 桶排序(Bucket sort)
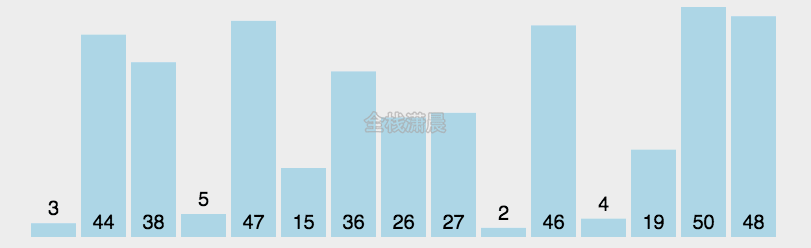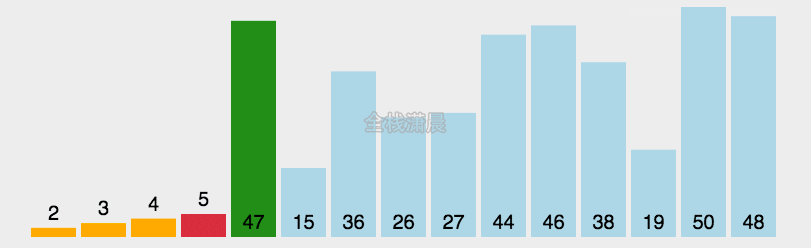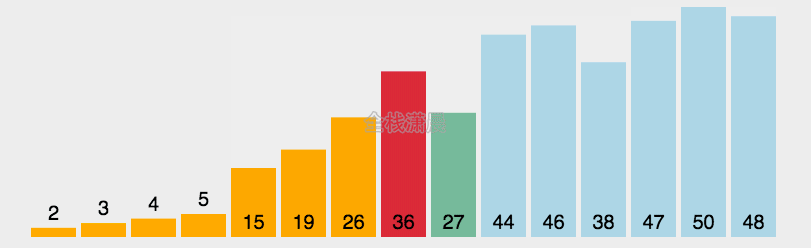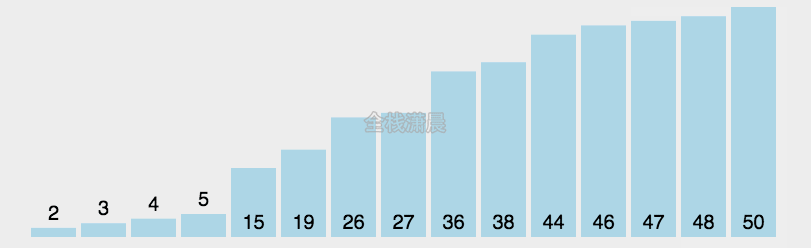
桶排序是将待排序集合中处于同一个值域的元素存入同一个桶中,也就是根据元素值特性将集合拆分为多个区域,则拆分后形成的多个桶,从值域上看是处于有序状态的。对每个桶中元素进行排序,则所有桶中元素构成的集合是已排序的。适用于待排序数据值域较大但分布比较均匀的情况。
快速排序是将集合拆分为两个值域,这里称为两个桶,再分别对两个桶进行排序,最终完成排序。桶排序则是将集合拆分为多个桶,对每个桶进行排序,则完成排序过程。两者不同之处在于,快排是在集合本身上进行排序,属于原地排序方式,且对每个桶的排序方式也是快排。桶排序则是提供了额外的操作空间,在额外空间上对桶进行排序,避免了构成桶过程的元素比较和交换操作,同时可以自主选择恰当的排序算法对桶进行排序。
当然桶排序更是对计数排序的改进,计数排序申请的额外空间跨度从最小元素值到最大元素值,若待排序集合中元素不是依次递增的,则必然有空间浪费情况。桶排序则是弱化了这种浪费情况,将最小值到最大值之间的每一个位置申请空间,更新为最小值到最大值之间每一个固定区域申请空间,尽量减少了元素值大小不连续情况下的空间浪费情况。
- 关键环节:
(1)元素值域的划分,也就是元素到桶的映射规则。映射规则需要根据待排序集合的元素分布特性进行选择,若规则设计的过于模糊、宽泛,则可能导致待排序集合中所有元素全部映射到一个桶上,则桶排序向比较性质排序算法演变。若映射规则设计的过于具体、严苛,则可能导致待排序集合中每一个元素值映射到一个桶上,则桶排序向计数排序方式演化。
(2)排序算法的选择,从待排序集合中元素映射到各个桶上的过程,并不存在元素的比较和交换操作,在对各个桶中元素进行排序时,可以自主选择合适的排序算法,桶排序算法的复杂度和稳定性,都根据选择的排序算法不同而不同。
- 工作原理:
1、设置一个定量的数组当作空桶;
2、遍历序列,并将元素一个个放到对应的桶中;
3、对每个不是空的桶进行排序(内层排序);
4、从不是空的桶里把元素再放回原来的序列中。
- 稳定性:
如果使用稳定的内层排序,并且将元素插入桶中时不改变元素间的相对顺序,那么桶排序就是一种稳定的排序算法。由于每块元素不多,一般使用插入排序。此时桶排序是一种稳定的排序算法。
- 复杂度:
对于待排序序列大小为 N,共分为 M 个桶,主要步骤有:
(1)N 次循环,将每个元素装入对应的桶中
(2)M 次循环,对每个桶中的数据进行排序(平均每个桶有 N/M 个元素)
一般使用较为快速的排序算法,时间复杂度为 O ( N l o g N ) O ( N l o g N ) O(NlogN),实际的桶排序过程是以链表形式插入的。
时间复杂度为:
O ( N ) + O ( M ∗ ( N / M ∗ l o g ( N / M ) ) ) = O ( N ∗ ( l o g ( N / M ) + 1 ) ) O ( N ) + O ( M ∗ ( N / M ∗ l o g ( N / M ) ) ) = O ( N ∗ ( l o g ( N / M ) + 1 ) ) O(N)+O(M∗(N/M∗log(N/M)))=O(N∗(log(N/M)+1))
当 N = M 时,复杂度为 O ( N ) O ( N ) O(N)
平均时间复杂度为 O ( n + k ) O ( n + k ) O(n+k),最坏的情况为 O ( n 2 ) O(n^2) O(n2)
空间复杂度: O ( N + M ) O(N + M) O(N+M)
代码:
#include <iostream>
#include <vector>
using namespace std;
void bucketSort(int data[], int len){
// 找到待排序数组的最值
int min = data[0];
int max = min;
for(int i = 1; i < len; i++){
if(data[i] < min) min = data[i];
if(data[i] > max) max = data[i];
}
// 计算桶的数量(元素值域的划分)
int bucketCounts = (max-min)/len + 1;
vector<vector<int>> bucketArrays;
for(int i = 0; i < bucketCounts; i++){
// position 0 used to keep the data count store in this bucket
vector<int> bucket;
bucketArrays.push_back(bucket);
}
// 遍历序列,并将元素一个个放到对应的桶中
for(int j = 0; j < len; j++){
int num = (data[j] -min) / len;
bucketArrays[num].push_back(data[j]);
}
// 对每个不是空的桶进行排序(内层排序)
for(int i = 0; i < bucketCounts; i++){
std::sort(bucketArrays[i].begin(), bucketArrays[i].end());
}
int index = 0;
// 根据排序后桶的数据 重新赋值到原数组中
for(int k = 0; k < bucketCounts; k++){
for(int s = 0; s < bucketArrays[k].size(); s++){
data[index++] = bucketArrays[k][s];
}
}
}
int main() {
int arr[10] = {18,11,28,45,23,50};
bucketSort(arr, 6);
for(int i = 0; i < 6; i++)
cout << arr[i] << endl;
return 0;
}
10. 基数排序(Radix sort)
一种非比较型的排序算法,最早用于解决卡片排序的问题。
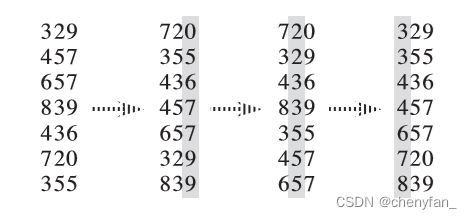
- 工作原理:
将待排序的元素拆分为 k k k 个关键字(比较两个元素时,先比较第一关键字,如果相同再比较第二关键字……),然后先对第 k k k 关键字进行稳定排序,再对第 k − 1 k-1 k−1 关键字进行稳定排序,再对第 k − 2 k-2 k−2 关键字进行稳定排序……最后对第一关键字进行稳定排序,这样就完成了对整个待排序序列的稳定排序。
基数排序需要借助一种 稳定算法 完成 内层对关键字的排序。 - 稳定性:
基数排序是一种稳定排序算法。 - 复杂度:
(1)时间复杂度:O(K * (N + M)),N为数组长度,M为值域大小,K为执行的计数排序次数(最大长度)。
(2)空间复杂度:O(N + M),N为数组长度,M为值域大小。 - 说明:
通常而言,基数排序比基于比较的排序算法(比如快速排序)要快。但由于需要额外的内存空间,因此当内存空间稀缺时,原地置换算法(比如快速排序)或许是个更好的选择。
在进行关键字排序时,通常已知值域大小,且不会很大,因此可以用计数排序进行内层排序。
但是普通的计数排序无法保证稳定性,因此需要对其进行改动,实现稳定的计数排序。
主要的思路就是,首先用数组统计每位数出现的次数,然后对统计数组进行前缀和计算,此时数组为最后一个该位数到数组首位的长度;然后再从后往前遍历待排序序列,将元素放到相应的位置上(长度-1),同时该位长度元素也减一,以此来实现稳定的计数排序。
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
void RadixSort(vector<int> &nums){
int len = 0;
int n = nums.size();
int maxNum = nums[0];
for(int i = 1; i < n; ++i){
if(maxNum < nums[i]) maxNum = nums[i]; // 找最大值
}
while(maxNum > 0){
++len; // 求最大值的位数
maxNum = maxNum / 10;
}
// LSD,从低位到高位,i = 1~len
vector<int> temp(nums);
for(int i = 1; i <= len; ++i){
// 稳定的计数排序过程
vector<int> count(10, 0);
for(int j = 0; j < n; ++j){
int bitNum = nums[j] / (int)pow(10, i-1) % 10; // 第i位上的数
++count[bitNum]; // count[bitNum]统计bitNum出现的次数
}
for(int j = 1; j < 10; ++j){
count[j] += count[j-1]; // 计数前缀和,此时记录的非次数,而是位置
}
// 从后往前遍历数组,count[bitNum]-1即为最后一个该位数的下标索引
for(int j = n - 1; j >= 0; --j){
int bitNum = nums[j] / (int)pow(10, i-1) % 10;
temp[count[bitNum]-1] = nums[j];// 临时排序数组
--count[bitNum]; // 索引减一,稳定计数排序
}
nums = temp; // 数组赋值
cout << "len = " << i << endl;
for(int i = 0; i < nums.size(); i++){
cout << nums[i] << " ";
}
}
}
int main(){
vector<int> nums = {113,212,510,12,28,1049,5,51,62};
RadixSort(nums);
for(int i = 0; i < nums.size(); i++){
cout << nums[i] << " ";
}
return 0;
}
- 基数排序对字符串进行排序:
#include <iostream>
#include <vector>
#include <cmath>
#include <string>
using namespace std;
void RadixSort(vector<string> &strs){
int n = strs.size();
int len = strs[0].length();
for(int i = 1; i < n; ++i){
if(len < strs[i].length()) len = strs[i].length(); // 找最大值
}
// LSD,从低位到高位,i = 0~len-1
vector<string> temp(strs);
for(int i = 0; i < len; ++i){
// 稳定的计数排序过程
vector<int> count(128, 0); // 128个ASCII字符,只有字母时可以缩减
for(int j = 0; j < n; ++j){
if(i >= strs[j].length()){ // 当前字符长度不够,该位为0
++count[0];
}else{
char bitChar = strs[j][i];
++count[bitChar]; // count[bitChar]统计bitChar出现的次数
}
}
for(int j = 1; j < 128; ++j){
count[j] += count[j-1]; // 计数前缀和,此时记录的非次数,而是位置
}
// 从后往前遍历数组,count[bitChar]-1即为最后一个该位字符的下标索引
for(int j = n - 1; j >= 0; --j){
if(i >= strs[j].length()){ // 当前字符长度不够,该位为0
temp[count[0]-1] = strs[j];
--count[0];
}else{
char bitChar = strs[j][i];
temp[count[bitChar]-1] = strs[j];// 临时排序数组
--count[bitChar]; // 索引减一,稳定计数排序
}
}
strs = temp; // 数组赋值
cout << "len = " << i << endl;
for(int i = 0; i < strs.size(); i++){
cout << strs[i] << " ";
}
cout << endl;
}
}
int main(){
vector<string> strs = {"saff","ahd","nmd","rqw","osg","zzzzz","pdgh","ga"};
RadixSort(strs);
for(int i = 0; i < strs.size(); i++){
cout << strs[i] << " ";
}
return 0;
}
11. 外部排序
当所要排序的的数据量太多或者文件太大,无法直接在内存里排序,而需要依赖外部设备(磁盘)时,就会使用到外部排序(归并思想)。
-
假设文件需要分成 k 块读入,需要从小到大进行排序。
-
依次读入每个文件块,在内存中对当前文件块进行排序并存储(应用恰当的内排序算法),此时,每块文件相当于一个由小到大排列的有序队列;
-
在内存中建立一个最小堆,读入每块文件的队列头;
-
弹出堆顶元素,如果元素来自第 i 块,则从第i块文件中补充一个元素到最小值堆,弹出的元素暂存至临时数组;
-
当临时数组存满时,将数组写至磁盘,并清空数组内容;
-
重复过程3、4,直至所有文件块读取完毕。
#include <bits/stdc++.h>
using namespace std;
vector<int> fun1(string str)
{
ifstream inFile(str);
vector<int> vec;
int temp;
for (int j = 1; j <= 2000; ++j)
{
inFile >> temp;
vec.push_back(temp);
}
return vec;
}
int main(int argc, char const *argv[])
{
clock_t start_time = clock();
static default_random_engine e;
static uniform_int_distribution<unsigned> u(0, 1000);
const int k = 5;
int temp;
ofstream outFile("input.txt");
ifstream inFile("input.txt");
ofstream outFile1("input1.txt");
ofstream outFile2("input2.txt");
ofstream outFile3("input3.txt");
ofstream outFile4("input4.txt");
ofstream outFile5("input5.txt");
//随机产生一万个小于1000的数据
for (size_t i = 0; i < 10000; ++i)
outFile << u(e) << " ";
//把一个文件中的数据分割到k个小文件中
for (int i = 0; i < 10000; ++i)
{
inFile >> temp;
switch (i/2000)
{
case 0 : outFile1 << temp << " "; break;
case 1 : outFile2 << temp << " "; break;
case 2 : outFile3 << temp << " "; break;
case 3 : outFile4 << temp << " "; break;
case 4 : outFile5 << temp << " "; break;
}
}
//分别读取k个文件中的数据放在vector中
vector<vector<int>> vec;
vec.push_back(fun1(string("input1.txt")));
vec.push_back(fun1(string("input2.txt")));
vec.push_back(fun1(string("input3.txt")));
vec.push_back(fun1(string("input4.txt")));
vec.push_back(fun1(string("input5.txt")));
//定义排序输出文件
ofstream outFile_result("output.txt");
for (int m = 0; m < 10000; ++m)
{
int j, min = 1001;
//分别每个文件中的数据建立最小堆
for (int i = 0; i < k; ++i)
make_heap(vec[i].begin(), vec[i].end(), greater<int>());
for (int i = 0; i < k; ++i)
{
if (vec[i][0] < min)
{
min = vec[i][0];
j = i;
}
}
//取所有文件最小堆中的最小值输出
outFile_result << min << " ";
//删除该最小值,重新建堆
pop_heap(vec[j].begin(), vec[j].end());
vec[j].pop_back();
}
clock_t end_time = clock();
cout << "Running time is: " << static_cast<double>(end_time-start_time)/CLOCKS_PER_SEC*1000 <<
"ms" << endl;//输出运行时间。
system("pause");
return 0;
}