逻辑回归简介
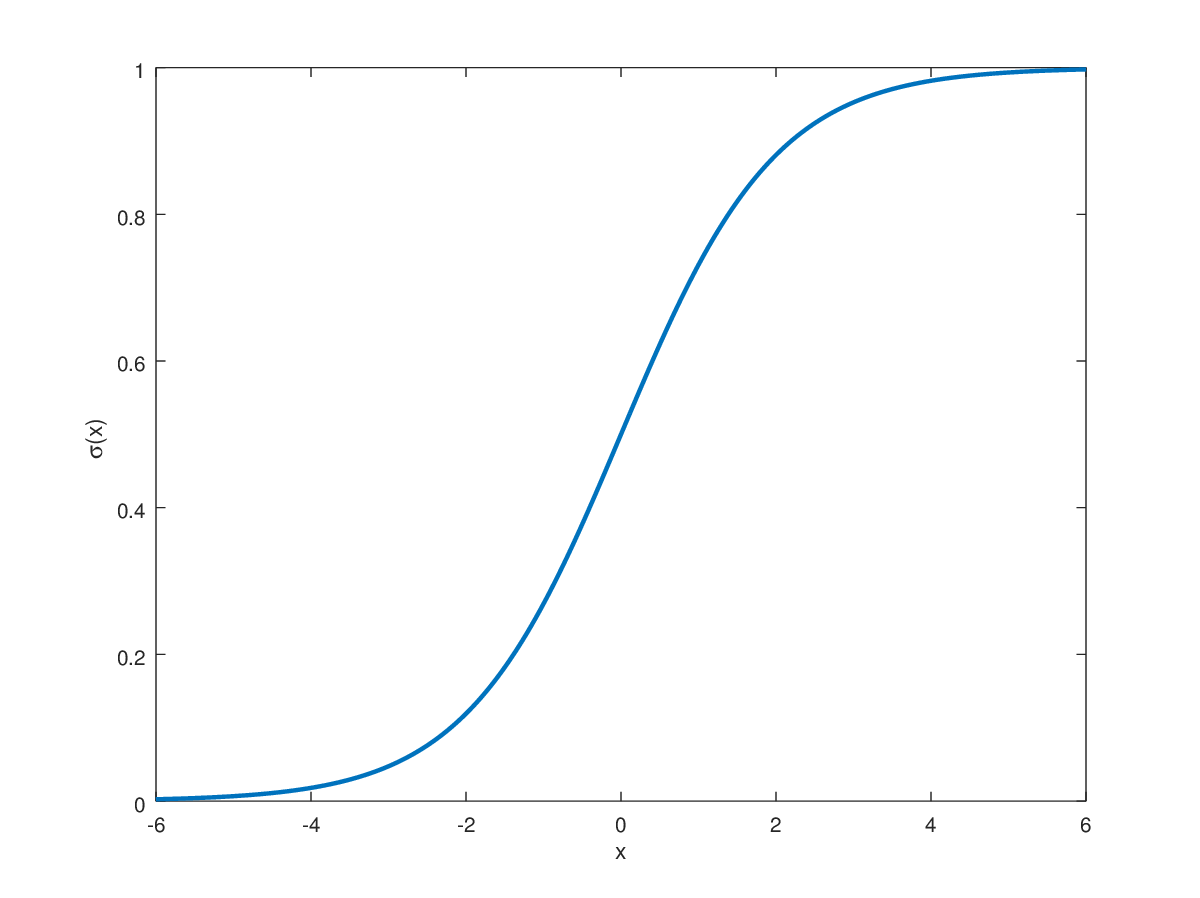
- sigmoid函数:
g ( z ) = 1 1 + e − z g(z) = \frac{1}{1+e^{-z}} g(z)=1+e−z1
- 逻辑回归假设函数:
y ^ = h θ ( x ) = g ( θ T x ) = 1 1 + e − θ T x \hat{y} = h_{\theta}(x) = g(\theta^Tx) = \frac{1}{1+e^{-\theta^Tx}} y^=hθ(x)=g(θTx)=1+e−θTx1
其中
θ
T
\theta^T
θT和
x
x
x延续在梯度下降算法在线性回归中的应用一文中的表达,即:
θ
T
=
[
θ
0
,
θ
1
,
θ
2
,
⋯
,
θ
n
]
x
=
[
x
0
x
1
x
2
⋮
x
n
]
\theta^T = \begin{bmatrix} \theta_0, \theta_1,\theta_2,\cdots,\theta_n \end{bmatrix}\\ x = \begin{bmatrix} x_0\\ x_1\\ x_2\\ \vdots\\ x_n \end{bmatrix}\\
θT=[θ0,θ1,θ2,⋯,θn]x=
x0x1x2⋮xn
- 损失函数:
L ( y ^ , y ) = − y l o g ( y ^ ) − ( 1 − y ) l o g ( 1 − y ^ ) L(\hat{y},y) = -ylog(\hat{y}) - (1-y)log(1-\hat{y}) L(y^,y)=−ylog(y^)−(1−y)log(1−y^)
- 损失函数可以这样理解,当某一样本的真实标签 y = 1 y=1 y=1(正类)时,损失函数变为:
L ( y ^ , y ) = − l o g ( y ^ ) L(\hat{y}, y) = -log(\hat{y}) L(y^,y)=−log(y^)
- 我们希望损失函数越小越好,那么也就是说希望 y ^ \hat{y} y^越大越好,而 y ^ \hat{y} y^表示是的概率,定义域是 [ 0 , 1 ] [0,1] [0,1], y ^ \hat{y} y^最大只能是1,与 y = 1 y = 1 y=1相同。
- 同样的,当某一样本的真实标签 y = 0 y=0 y=0(负类)时,损失函数变为:
L ( y ^ , y ) = l o g ( 1 − y ^ ) L(\hat{y},y) = log(1-\hat{y}) L(y^,y)=log(1−y^)
我们希望损失函数越小越好,那么也就是说希望 y ^ \hat{y} y^越小越好,而 y ^ \hat{y} y^表示是的概率,定义域是 [ 0 , 1 ] [0,1] [0,1], y ^ \hat{y} y^最小只能是0,与 y = 0 y = 0 y=0相同。
- 代价函数:
J ( θ ) = 1 m ∑ i = 1 m L ( y ^ ( i ) , y ( i ) ) = 1 m ∑ i = 1 m [ − y ( i ) l o g ( y ^ ( i ) ) − ( 1 − y ( i ) ) l o g ( 1 − y ^ ( i ) ) ] = 1 m ∑ i = 1 m [ − y ( i ) l o g ( 1 1 + e − θ T x ( i ) ) − ( 1 − y ( i ) ) l o g ( 1 1 + e − θ T x ( i ) ) ] \begin{align} J(\theta) &= \frac{1}{m}\sum^m_{i=1}L(\hat{y}^{(i)}, y^{(i)})\\ &= \frac{1}{m}\sum^m_{i=1}[-y^{(i)}log(\hat{y}^{(i)}) - (1-y^{(i)})log(1-\hat{y}^{(i)})]\\ &= \frac{1}{m}\sum^m_{i=1}\left[-y^{(i)} log\left(\frac{1}{1+e^{-\theta^Tx^{(i)}}}\right) - (1-y^{(i)})log\left(\frac{1}{1 + e^{-\theta^Tx^{(i)}}}\right)\right] \end{align} J(θ)=m1i=1∑mL(y^(i),y(i))=m1i=1∑m[−y(i)log(y^(i))−(1−y(i))log(1−y^(i))]=m1i=1∑m[−y(i)log(1+e−θTx(i)1)−(1−y(i))log(1+e−θTx(i)1)]
梯度下降算法求解逻辑回归
- J ( θ ) J(\theta) J(θ)对 θ j \theta_j θj求偏导, θ j \theta_j θj表示第 j j j个 θ \theta θ的值:
∂ ∂ θ j J ( θ ) = ∂ ∂ θ j 1 m ∑ i = 1 m [ − y ( i ) l o g ( 1 1 + e − θ T x ( i ) ) − ( 1 − y ( i ) ) l o g ( 1 1 + e θ T x ( i ) ) ] = 1 m ∑ i = 1 m [ y ( i ) l o g ( 1 + e − θ T x ( i ) ) + ( 1 − y ( i ) ) l o g ( 1 + e θ T x ( i ) ) ] \begin{align} \frac{\partial}{\partial\theta_j}J(\theta) &= \frac{\partial}{\partial\theta_j} \frac{1}{m}\sum^m_{i=1}\left[-y^{(i)} log\left(\frac{1}{1+e^{-\theta^Tx^{(i)}}}\right) - (1-y^{(i)})log\left(\frac{1}{1 + e^{\theta^Tx^{(i)}}}\right)\right]\\ &=\frac{1}{m}\sum^m_{i=1}\left[y^{(i)} log\left(1+e^{-\theta^Tx^{(i)}}\right) + (1-y^{(i)})log\left(1 + e^{\theta^Tx^{(i)}}\right)\right]\\ \end{align} ∂θj∂J(θ)=∂θj∂m1i=1∑m[−y(i)log(1+e−θTx(i)1)−(1−y(i))log(1+eθTx(i)1)]=m1i=1∑m[y(i)log(1+e−θTx(i))+(1−y(i))log(1+eθTx(i))]
- 对 l o g ( 1 + e θ T x ( i ) ) log\left(1+e^{\theta^Tx^{(i)}}\right) log(1+eθTx(i))求偏导,注意这里采用复合函数求导法则
∂ ∂ θ j l o g ( 1 + e − θ T x ( i ) ) = 1 1 + e − θ T x ( i ) × e − θ T x ( i ) × − x j ( i ) = − x j ( i ) e − θ T x ( i ) 1 + e − θ T x ( i ) \begin{align} \frac{\partial}{\partial\theta_j}log\left(1+e^{-\theta^Tx^{(i)}}\right) &= \frac{1}{1 + e^{-\theta^Tx^{(i)}}} \times e^{-\theta^Tx^{(i)}} \times -x^{(i)}_{j}\\ & = \frac{-x^{(i)}_{j}e^{-\theta^Tx^{(i)}}}{1 + e^{-\theta^Tx^{(i)}}} \end{align} ∂θj∂log(1+e−θTx(i))=1+e−θTx(i)1×e−θTx(i)×−xj(i)=1+e−θTx(i)−xj(i)e−θTx(i)
- 则,原式为:
∂ ∂ θ j J ( θ ) = 1 m ∑ i = 1 m [ − y ( i ) × − x j ( i ) e − θ T x ( i ) 1 + e − θ T x ( i ) + ( 1 − y ( i ) ) × x j ( i ) e θ T x ( i ) 1 + e θ T x ( i ) ] = 1 m ∑ i = 1 m [ − y ( i ) × − x j ( i ) e θ T x ( i ) + 1 + ( 1 − y ( i ) ) × x j ( i ) e θ T x ( i ) 1 + e θ T x ( i ) ] = 1 m ∑ i = 1 m [ − x j ( i ) y ( i ) + x j ( i ) e θ T x ( i ) − y ( i ) x j ( i ) e θ T x ( i ) 1 + e θ T x ( i ) ] = 1 m ∑ i = 1 m [ − y ( i ) ( 1 + e θ T x ( i ) ) + e θ T x ( i ) 1 + e θ T x ( i ) x j ( i ) ] = 1 m ∑ i = 1 m [ ( − y ( i ) + e θ T x ( i ) 1 + e θ T x ( i ) ) x j ( i ) ] = 1 m ∑ i = 1 m [ ( − y ( i ) + 1 e − θ T x ( i ) + 1 ) x j ( i ) ] = 1 m ∑ i = 1 m [ ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) ] \begin{align} \frac{\partial}{\partial\theta_j}J(\theta) &=\frac{1}{m}\sum^{m}_{i=1}\left[-y^{(i)} \times \frac{-x^{(i)}_{j}e^{-\theta^Tx^{(i)}}}{1 + e^{-\theta^Tx^{(i)}}} + (1-y^{(i)})\times\frac{x^{(i)}_{j}e^{\theta^Tx^{(i)}}}{1 + e^{\theta^Tx^{(i)}}}\right]\\ & = \frac{1}{m}\sum^{m}_{i=1}\left[-y^{(i)} \times \frac{-x^{(i)}_{j}}{e^{\theta^Tx^{(i)}} + 1} + (1-y^{(i)})\times\frac{x^{(i)}_{j}e^{\theta^Tx^{(i)}}}{1 + e^{\theta^Tx^{(i)}}}\right]\\ & = \frac{1}{m}\sum^{m}_{i=1}\left[\frac{-x_j^{(i)}y^{(i)} + x_j^{(i)}e^{\theta^Tx^{(i)}} - y^{(i)}x_j^{(i)}e^{\theta^Tx^{(i)}}}{1 + e^{\theta^Tx^{(i)}}}\right]\\ & = \frac{1}{m}\sum^{m}_{i=1}\left[\frac{-y^{(i)}(1 + e^{\theta^Tx^{(i)}}) + e^{\theta^Tx^{(i)}}}{1 + e^{\theta^Tx^{(i)}}} x_j^{(i)} \right]\\ & = \frac{1}{m}\sum^{m}_{i=1}\left[\left(-y^{(i)} + \frac{e^{\theta^Tx^{(i)}}}{1 + e^{\theta^Tx^{(i)}}}\right)x_j^{(i)}\right]\\ & = \frac{1}{m}\sum^{m}_{i=1}\left[\left(-y^{(i)} + \frac{1}{e^{-\theta^Tx^{(i)}} + 1}\right)x_j^{(i)}\right]\\ & = \frac{1}{m}\sum^{m}_{i=1}\left[\left(h_\theta\left(x^{(i)}\right)-y^{(i)}\right)x_j^{(i)}\right]\\ \end{align} ∂θj∂J(θ)=m1i=1∑m[−y(i)×1+e−θTx(i)−xj(i)e−θTx(i)+(1−y(i))×1+eθTx(i)xj(i)eθTx(i)]=m1i=1∑m[−y(i)×eθTx(i)+1−xj(i)+(1−y(i))×1+eθTx(i)xj(i)eθTx(i)]=m1i=1∑m[1+eθTx(i)−xj(i)y(i)+xj(i)eθTx(i)−y(i)xj(i)eθTx(i)]=m1i=1∑m[1+eθTx(i)−y(i)(1+eθTx(i))+eθTx(i)xj(i)]=m1i=1∑m[(−y(i)+1+eθTx(i)eθTx(i))xj(i)]=m1i=1∑m[(−y(i)+e−θTx(i)+11)xj(i)]=m1i=1∑m[(hθ(x(i))−y(i))xj(i)]
根据梯度下降算法公式,迭代公式为:
θ
j
:
=
θ
j
−
α
1
m
∑
i
=
1
m
[
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
x
j
(
i
)
]
\theta_j := \theta_j - \alpha\frac{1}{m}\sum^{m}_{i=1}\left[\left(h_\theta(x^{(i)}) - y^{(i)}\right)x_j^{(i)}\right]
θj:=θj−αm1i=1∑m[(hθ(x(i))−y(i))xj(i)]
上面的
:
=
:=
:=符号表示先算右边的式子,算完后赋值给左边的变量。注意:左边和右边的
θ
i
\theta_i
θi值并不相等,右边是迭代前的
θ
i
\theta_i
θi值,左边的迭代后
θ
i
\theta_i
θi的值。
python代码实现
- 导入必要包
import numpy as np
import statsmodels.api as sm
from tqdm.notebook import tqdm
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_california_housing, make_regression
- 读取数据函数
def load_data(data_path):
data = np.loadtxt(data_path,delimiter=',')
n = data.shape[1]-1
data_x = data[:,0:n]
data_y = data[:,-1].reshape(-1,1)
return data_x,data_y
- sigmoid函数
def sigmoid(z):
r = 1/(1 + np.exp(-z))
return r
- 逻辑回归函数
def logic_lr(data_x, theta):
z = np.dot(data_x,theta)
return sigmoid(z)
- 代价函数
def compute_loss(data_x, data_y, theta):
row_num, col_num = data_x.shape
l = -1 * data_y * np.log(logic_lr(data_x, theta)) - (1-data_y)*np.log(1-logic_lr(data_x, theta))
return np.sum(l)/row_num
- 梯度下降算法求解逻辑回归函数
def solve_logic_lr(data_x, data_y, theta, alpha, steps):
temp_ones = np.ones(data_x.shape[0]).transpose()
data_x = np.insert(data_x, 0, values=temp_ones, axis=1)
row_num, col_num = data_x.shape
loss_list = []
for step in range(steps):
loss_list.append(compute_loss(data_x, data_y, theta))
for i in range(col_num):
theta[i] = theta[i] - (alpha/row_num) * np.sum((logic_lr(data_x, theta) - data_y) * data_x[:,i].reshape(-1,1))
return theta, loss_list
- 预测函数
def predict(data_x, theta):
temp_ones = np.ones(data_x.shape[0]).transpose()
data_x = np.insert(data_x, 0, values=temp_ones, axis=1)
p = logic_lr(data_x, theta)
p[p >= 0.5] = 1
p[p < 0.5] = 0
return p
- 函数调用
data_x, data_y = load_data('/kaggle/input/studyml/cls.txt')
data_x, mu, sigma = data_std(data_x)
# 变成列向量
theta = np.zeros(data_x.shape[1]+1).reshape(-1,1)
steps = 100
alpha = 0.0001
theta, loss = solve_logic_lr(data_x, data_y, theta, alpha, steps)
print(theta)
# 打印输出:[0.0009, 0.0027, 0.00249]
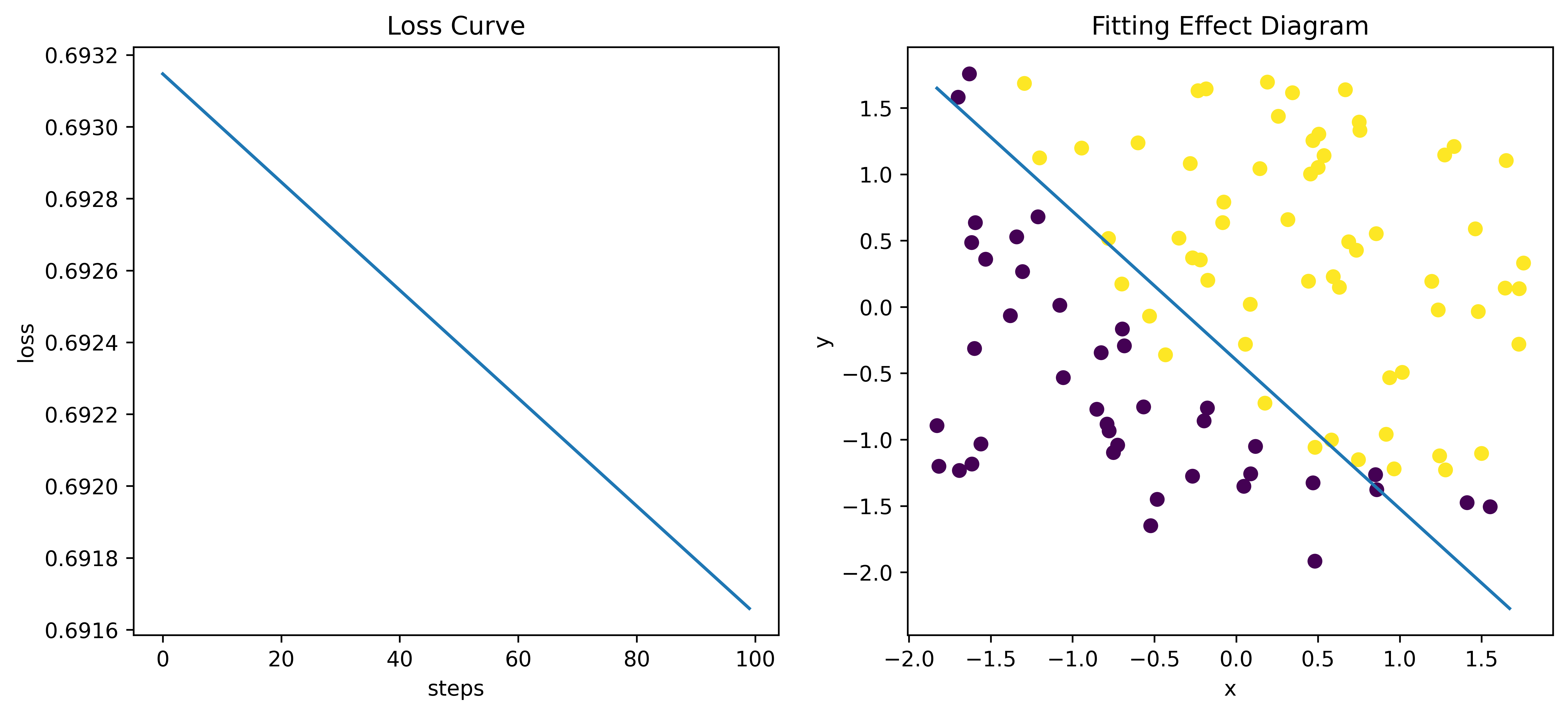
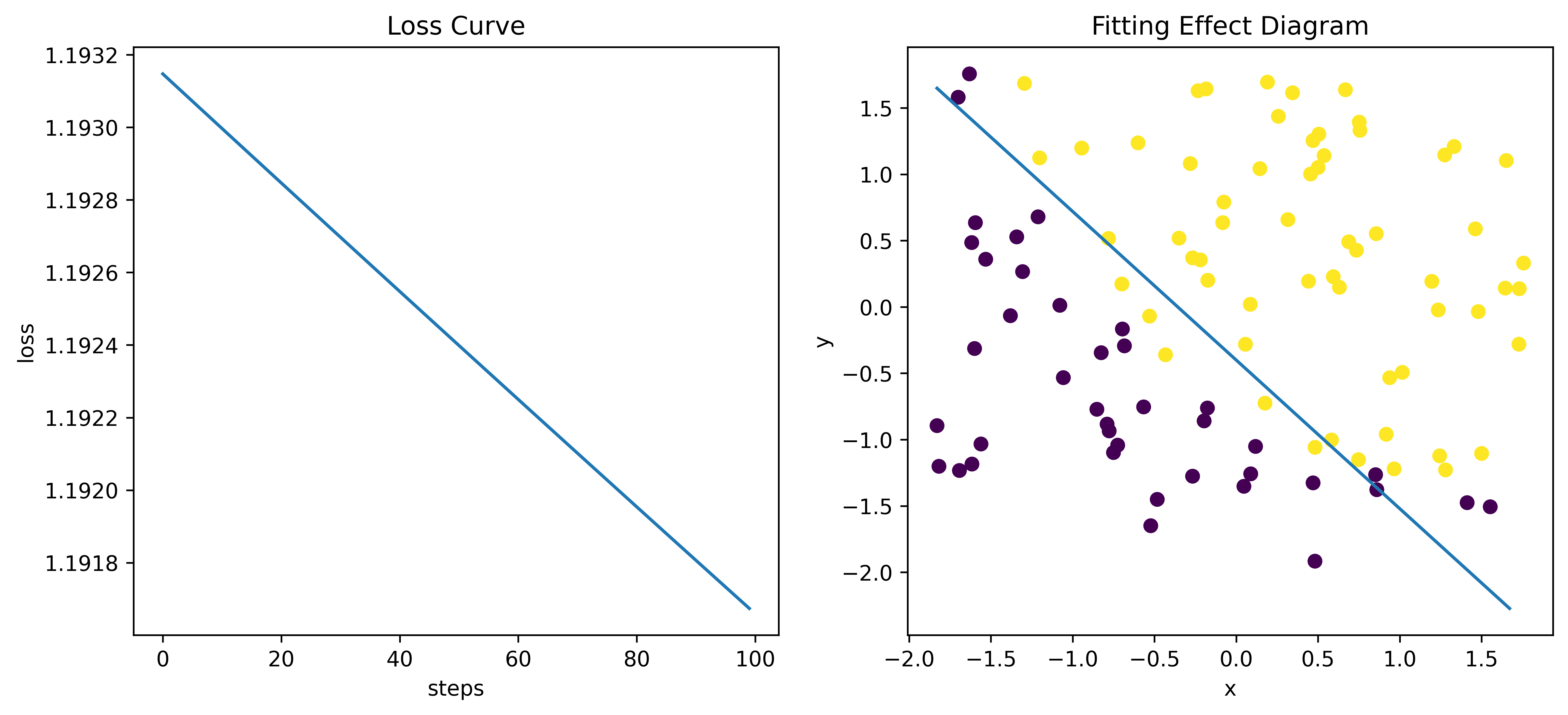
- 绘制Loss曲线(左)和拟合效果图(右)
plt.figure(figsize=(12,5),dpi=600)
plt.subplot(1,2,1)
plt.plot(loss)
plt.title("Loss Curve")
plt.xlabel("steps")
plt.ylabel("loss")
plt.subplot(1,2,2)
plt.scatter(data_x[:,0],data_x[:,1],c=data_y)
temp_x1 = np.arange(min(data_x[:,0]), max(data_x[:,0]), 0.1)
temp_x2 = -(theta[1] * temp_x1 + theta[0])/theta[2]
plt.plot(temp_x1, temp_x2)
plt.title("Fitting Effect Diagram")
plt.xlabel("x")
plt.ylabel("y")
plt.show()
带L2正则化的逻辑回归
- 引入L2正则化,用于惩罚大的回归系数,减轻过拟合。则代价函数变为:
J ( θ ) = 1 m ∑ i = 1 m [ − y ( i ) l o g ( 1 1 + e − θ T x ( i ) ) − ( 1 − y ( i ) ) l o g ( 1 1 + e − θ T x ( i ) ) ] + λ 2 m ∥ θ ∥ 2 2 \begin{align} J(\theta) &= \frac{1}{m}\sum^m_{i=1}\left[-y^{(i)} log\left(\frac{1}{1+e^{-\theta^Tx^{(i)}}}\right) - (1-y^{(i)})log\left(\frac{1}{1 + e^{-\theta^Tx^{(i)}}}\right)\right] + \frac{\lambda}{2m}\lVert \theta \rVert_2^2 \end{align} J(θ)=m1i=1∑m[−y(i)log(1+e−θTx(i)1)−(1−y(i))log(1+e−θTx(i)1)]+2mλ∥θ∥22
- 根据上述的推导,可以得到 J ( θ ) J(\theta) J(θ)对 θ j \theta_j θj的偏导数为:
∂ ∂ θ j J ( θ ) = 1 m ∑ i = 1 m [ ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) ] + 1 m × λ θ j \frac{\partial}{\partial\theta_j}J(\theta) = \frac{1}{m}\sum^{m}_{i=1}\left[\left(h_\theta\left(x^{(i)}\right)-y^{(i)}\right)x_j^{(i)}\right] + \frac{1}{m} \times \lambda\theta_j ∂θj∂J(θ)=m1i=1∑m[(hθ(x(i))−y(i))xj(i)]+m1×λθj
根据梯度下降算法公式,迭代公式为:
θ
j
:
=
θ
j
−
α
1
m
∑
i
=
1
m
[
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
x
j
(
i
)
+
λ
θ
j
]
\theta_j := \theta_j - \alpha\frac{1}{m}\sum^{m}_{i=1}\left[\left(h_\theta(x^{(i)}) - y^{(i)}\right)x_j^{(i)} + \lambda\theta_j \right]
θj:=θj−αm1i=1∑m[(hθ(x(i))−y(i))xj(i)+λθj]
python代码实现
- 在上面的基础上,只需要修改代价函数和梯度下降求解函数就可以了
- 代价函数变为:
def compute_loss(data_x, data_y, theta, lambd):
row_num, col_num = data_x.shape
l = -1 * data_y * np.log(logic_lr(data_x, theta)) - (1-data_y)*np.log(1-logic_lr(data_x, theta))
return np.sum(l)/row_num + (lambd/2*row_num) + np.sum(np.power(theta,2))
- 梯度下降求解函数变为:
def solve_logic_lr(data_x, data_y, theta, alpha, steps, lambd=0.01):
temp_ones = np.ones(data_x.shape[0]).transpose()
data_x = np.insert(data_x, 0, values=temp_ones, axis=1)
row_num, col_num = data_x.shape
loss_list = []
for step in range(steps):
loss_list.append(compute_loss(data_x, data_y, theta, lambd))
for i in range(col_num):
theta[i] = theta[i] - (alpha/row_num) * np.sum((logic_lr(data_x, theta) - data_y) * data_x[:,i].reshape(-1,1) + lambd * theta[i])
return theta, loss_list
- 函数调用
data_x, data_y = load_data('/kaggle/input/studyml/cls.txt')
data_x, mu, sigma = data_std(data_x)
# 变成列向量
theta = np.zeros(data_x.shape[1]+1).reshape(-1,1)
steps = 100
alpha = 0.0001
theta, loss = solve_logic_lr(data_x, data_y, theta, alpha, steps)
print(theta)
- 绘制Loss曲线(左)和拟合效果图(右)
plt.figure(figsize=(12,5),dpi=600)
plt.subplot(1,2,1)
plt.plot(loss)
plt.title("Loss Curve")
plt.xlabel("steps")
plt.ylabel("loss")
plt.subplot(1,2,2)
plt.scatter(data_x[:,0],data_x[:,1],c=data_y)
temp_x1 = np.arange(min(data_x[:,0]), max(data_x[:,0]), 0.1)
temp_x2 = -(theta[1] * temp_x1 + theta[0])/theta[2]
plt.plot(temp_x1, temp_x2)
plt.title("Fitting Effect Diagram")
plt.xlabel("x")
plt.ylabel("y")
plt.show()