正则表达式匹配C++代码实现

正则表达式匹配的解决需要用到递归和动态规划的知识。

递归和动态规划之间是有密切的联系的。动态规划的实质就是带有缓存区的递归。

递归实现阶乘。


#include <iostream>

using namespace std;

 

//计算阶乘的函数

long CalcJiecheng(int num)

{

	int res = 0;

    if (1== num) //边界条件

    {

		res = 1;

    }

	if (num>1)  //递归公式

	{

		res = num*CalcJiecheng(num-1);

	}

	return res;

}

 

int main()

{

	long res = CalcJiecheng(5);

	cout<<"5的阶乘:"<<res<<endl;

	system("pause");

	return 0;

}

动态规划会有一个状态转移方程来存取每次递归调用的状态值，这样算法的效率会有所提高，就会省去很多的重复计算。

动态规划算法的难点在于从实际问题中抽象出动态规划表dp，dp一般是一个数组，可能是一维的也可能是二维的，也可能是其他的数据结构：整个求解过程就可以用一个最优决策表来描述，最优决策表可以是一个二维表，其中行表示决策的阶段，列表示问题状态，表格需要填写的数据一般对应此问题的在某个阶段某个状态下的最优值（如最短路径，最长公共子序列，最大价值等），填表的过程就是根据递推关系，从1行1列开始，以行或者列优先的顺序，依次填写表格，最后根据整个表格的数据通过简单的取舍或者运算求得问题的最优解：
f(n,m)=max{f(n-1,m), f(n-1,m-w[n])+P(n,m)}
————————————————
版权声明：本文为CSDN博主「MISAYAONE」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/misayaaaaa/article/details/71940779

递归调用最简单也是最经典的例子就是台阶问题。

有n级台阶，一个人每次上一级或者两级，问有多少种走完n级台阶的方法？

n阶台阶，只可能是从n-1或是n-2的台阶上走上来的，台阶n的阶段依赖的是n-1和n-2的子阶段，所以状态转移方程为dp[n] = dp[n-1] + dp[n-2]，属于最简单的动态规划问题


#include <iostream>

 

#define N 20        //台阶数为20

using namespace std;

 

int dp[N];          //全局数组，存放决策表

 

int fun(int n)      //返回台阶数为n的走法

{

	if (n == 1 || n == 2)

	{

		return n;

	}

	dp[n-1] = fun(n-1);        //若不为1或2则进行递归计算

	dp[n-2] = fun(n-2);

	dp[n] = dp[n-1]+dp[n-2];   //状态转移方程

	return dp[n];

}

 

int main(int argc,char** argv)

{

	fun(N);

	cout<<dp[15]<<endl;        //输出15阶的走法

	system("pause");

	return 0;

}

铺垫完毕，言归正传。

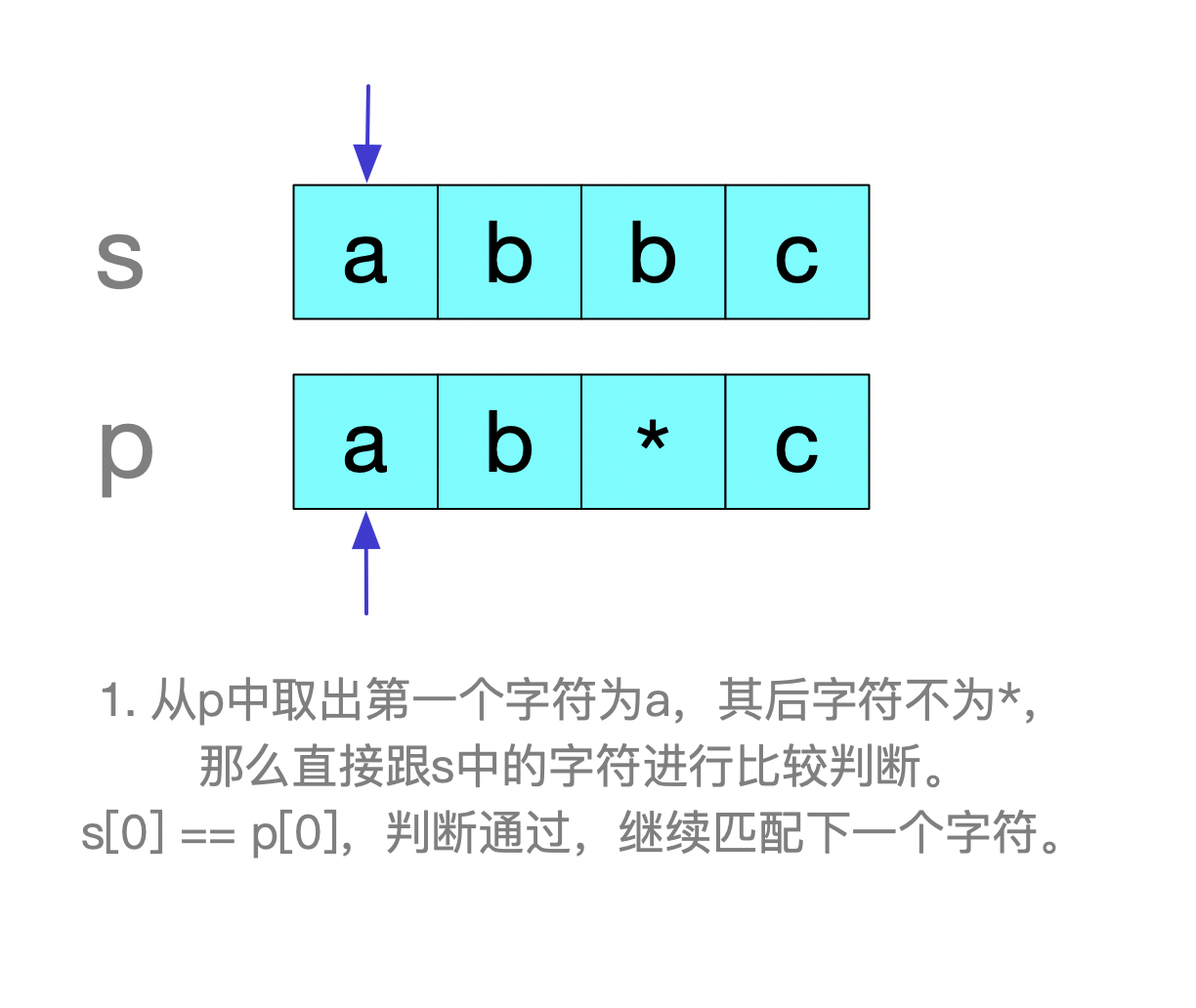
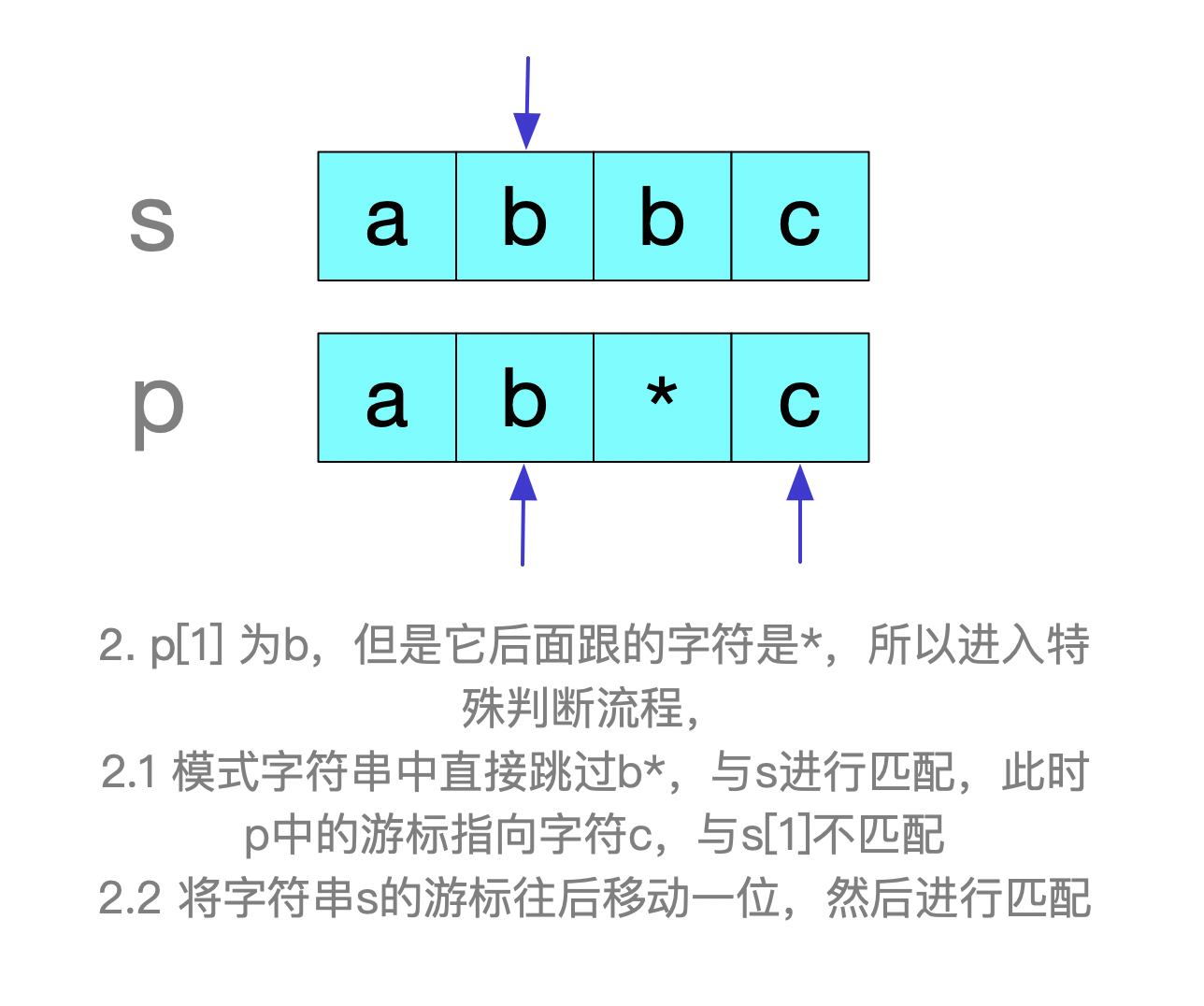
在匹配字符的过程中需要分类讨论。如果p中有.字符，那么很好办，因为它是万能字符，我们直接跳过就可以，在程序中就是直接判为1.如果P中有*号可能就会麻烦些。我们需要重点讨论下带*和不带*的情况。不带*号也好办，只要和s中的字符逐一对比就行。如果带字符*就需要分两种情况。见图

分析完毕上代码

class Solution
{
	public:
		bool isMatch(string s,string p)
		{
			return isMatch(s.c_str(),p.c_str());
		}
		bool isMatch(const char*s,const char *p)
		{
			if(*p==0)
			return *s==0;
			auto first_match=*s&&(*s==*p||*p=='.');
			if(*(p+1)=='*')
			{
				return isMatch(s,p+2)||(first_match && isMatch(++s,p));
			}
			else 
			{
				return first_match && isMatch(++s,++p);
			}
		}
 } ;

正则表达式匹配C++代码实现

悦读