欢迎访问我的博客首页。
LOAM
1. LOAM 概述
1.1 主要贡献
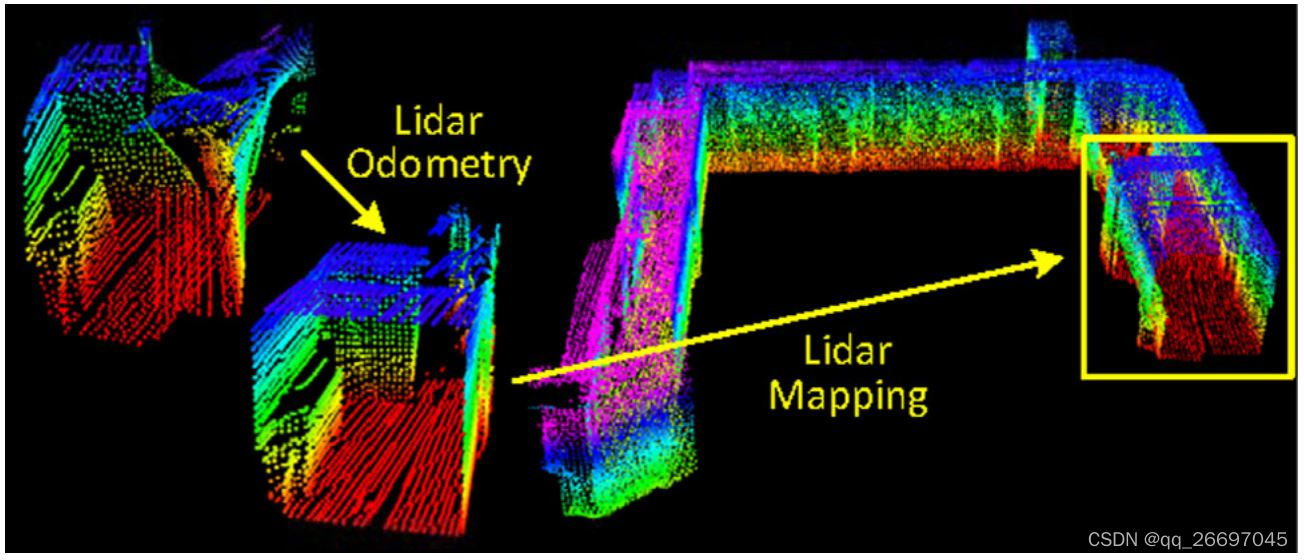
LOAM 旨在使用一个运动的三维激光雷达进行运动估计和地图创建。由于采集时刻不同,运动的激光雷达采集到的点存在畸变,如左侧的点云。LOAM 使用两个并行的算法解决这个问题:里程计算法估计激光雷达的速度并校正点云畸变;建图算法匹配并注册点云到地图中。
1.2 硬件
北阳 UTM-30LX 是单线二维激光雷达,它的激光发射器沿水平方向转动,每隔 0.25° 发射一个激光束。所以其水平分辨率是
0.25
0.25
0.25°。
为了实现三维扫描,激光雷达被安装在一个电机上。该电机以 40 转每秒的速度,在竖直方向的 180° 范围内以逐行扫描的方式扫描 40 行。所以其竖直分辨率是 180 ÷ 40 = 4.5 180 \div 40 = 4.5 180÷40=4.5°。
北阳电机提供激光雷达上位机软件 UrgBenri,可以很方便的进行数据的采集、显示、存储。下面是 UrgBenri 存储的数据内容,第 28 行是激光发射器旋转 270° 采集到的 270 ÷ 0.25 = 1080 270 \div 0.25 = 1080 270÷0.25=1080 个点,第 30 行是采集第一个点时的时间戳。
[model]
UTM-30LX(Hokuyo Automatic Co.,Ltd.)
[frontStep]
540
[minDistance]
23
[maxDistance]
60000
[motorSpeed]
2400
[totalSteps]
1440
[captureMode]
GD_Capture_mode
[scanMsec]
25
[startStep]
0
[endStep]
1080
[serialNumber]
00904066
[timestamp]
793464
[logtime]
2013:1:12:15:6:32:312
[scan]
392;397;398;400;403;403;407;409;409;409;411;411;422;424;424;422;420;...
[timestamp]
793514
[logtime]
2013:1:12:15:6:32:351
[scan]
上面的 1080 个点是一次扫描(scan)采集到的点。电机完成一轮逐行扫描,产生 1080 × 40 = 4.32 1080 \times 40 = 4.32 1080×40=4.32 万个点,称为一次扫描覆盖(sweep)。
1.3 符号表示与任务描述
LOAM 的任务是,根据三维雷达采集的点云估计雷达自身的运动,并对遍历过的场景建图。LOAM 假设雷达内参已标定且内部运动学已知。内存已标定,就可以对雷达点进行 3D 投影。还假设雷达的角速度和线速度是平滑且连续的,该假设使用 IMU 实现。
小写的右下角标 k k k 代表第 k k k 次扫描覆盖。一次扫描覆盖采集到的点云用 P k {\mathcal P}_k Pk 表示。第 k k k 次扫描覆盖的开始时刻用 t k t_k tk 表示。
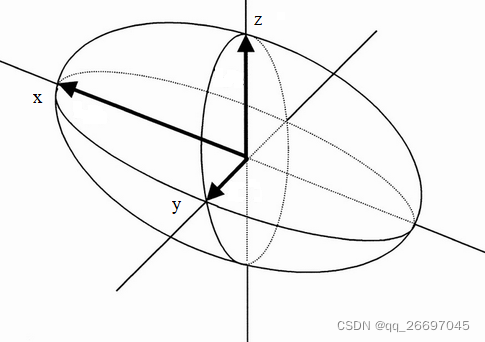
大写的右上角标 L L L、 W W W 代表坐标系。激光雷达坐标系 L L L 是一个三维坐标系,原点在雷达的几何中心, x x x 轴向左, y y y 轴向上, z z z 轴向前,如图 2。激光雷达第 k k k 次扫描覆盖采集到的点 i i i 在雷达坐标系中的坐标用 X ( k , i ) L X_{(k, i)}^L X(k,i)L 表示。 T k L ( t ) T_k^L(t) TkL(t) 表示把雷达在时刻 t t t 采集到的一个点投影到时刻 t k t_k tk 所对应的变换(投影就是坐标变换)。
世界坐标系 W W W 与激光雷达初始坐标系重合。激光雷达第 k k k 次扫描覆盖采集到的点 i i i 在世界坐标系中的坐标用 X ( k , i ) W X_{(k, i)}^W X(k,i)W 表示。 T k W ( t ) T_k^W(t) TkW(t) 表示把采集于时刻 t t t 的一点投影到世界坐标系所对应的变换。
LOAM(lidar odometry and mapping)问题可以概况为:求点云 P k {\mathcal P}_k Pk 的位姿,并用这些点云创建地图。
1.4 软件
每个扫描过程中,都会把激光雷达采集到的点 P ^ \hat \mathcal P P^ 变换到激光雷达坐标系 L L L 中,得到 P \mathcal P P。
第 k k k 次扫描采集的点云 P k {\mathcal P}_k Pk 会被两个算法处理:里程计算法计算两次连续扫描间的激光雷达运动;运动估计算法对 P \mathcal P P 祛畸变。这两个算法的工作频率是 10 赫兹。
算法的输出用于创建地图。创建地图时,把祛畸变的点云与地图匹配并加入地图,工作频率是 1 赫兹。
2. 特征点提取
点云 P k {\mathcal P}_k Pk 在横竖方向的分辨率不一样,即它不是均匀分布的。但是它的每行点云是共面的,40 行点云对应 40 个平面。因此,利用每行点云的共面关系提取特征点。
特征点包含边缘点和平面点。假设 i i i 是 P k \mathcal P_k Pk 中第 m m m 行 n n n 列的一点,局部点集 S \mathcal S S 是第 m m m 行第 n ± x n \pm x n±x 列点云。点云 i i i 的局部表面平滑性:
c = 1 ∣ S ∣ ⋅ ∣ ∣ X ( k , i ) L ∣ ∣ ∣ ∣ ∑ j ∈ S , j ≠ i ( X ( k , i ) L − X ( k , j ) L ) ∣ ∣ . (1) c = \frac{1} {| \mathcal S| \cdot || X_{(k, i)}^L ||} || \sum_{j \in \mathcal S, j \neq i}{} (X_{(k, i)}^L - X_{(k, j)}^L) ||. \tag{1} c=∣S∣⋅∣∣X(k,i)L∣∣1∣∣j∈S,j=i∑(X(k,i)L−X(k,j)L)∣∣.(1)
为了消除尺度影响,使用点
i
i
i 到激光雷达中心的距离
∣
∣
X
(
k
,
i
)
L
∣
∣
|| X_{(k, i)}^L ||
∣∣X(k,i)L∣∣ 除局部表面平滑性。
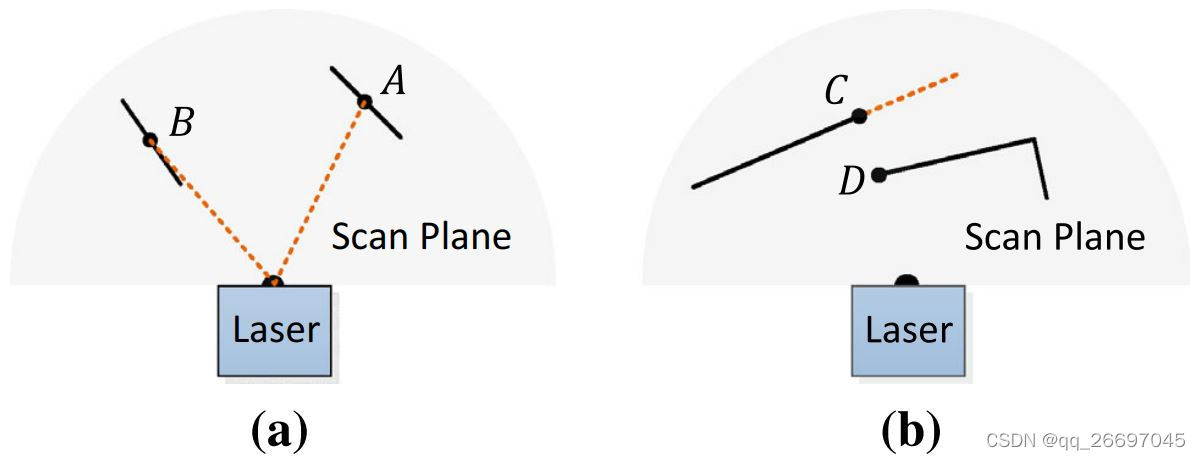
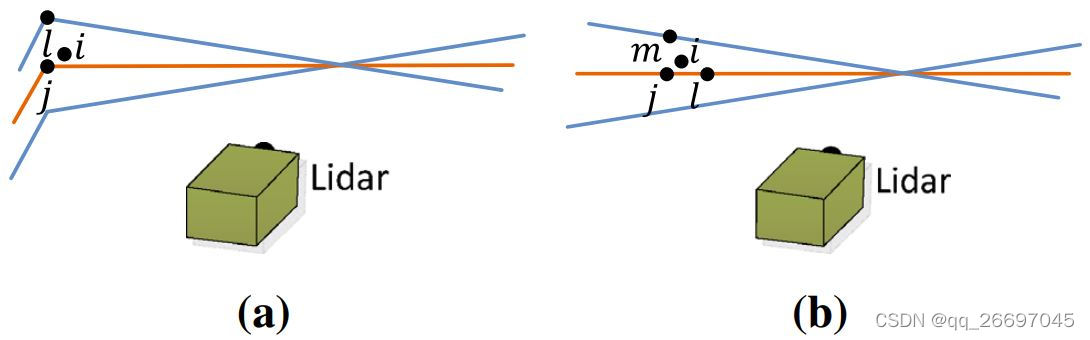
图 b 的实线代表可见区域,虚线代表遮挡区域。点 C 在可见区域与遮挡区域的边界,容易被误认为是边缘点,但换个角度就可以看到遮挡区域,因此它不可作为边缘点。点 D 在一个局部平面的边缘,也不被作为边缘点。
把一次扫描采集到的点按 c c c 的大小排序,再根据 c c c 的大小选择特征点:从大于阈值 5 × 1 0 − 3 5 \times 10^{-3} 5×10−3 的点中选择较大的点当作边缘点,从小于阈值 5 × 1 0 − 3 5 \times 10^{-3} 5×10−3 的点中选择较小的点当作平面点。为了使特征点均匀分布,把扫描平面分成四个子区域,在每个子区域中最多提取 2 个边缘点和 4 个平面点。特征点选取的注意事项:
- 特征点应该足够稀疏,即,特征点旁边的点不应再被当作特征点。
- 特征点所在的局部表面不应该与激光束平行,如图 4(a)。因为这样的点通常不可靠。
- 特征点不应该在遮挡区域的边界,如图 4(b)。由于橘色区域被遮挡,点 C C C 会被认为是边缘点。而实际上它是平面点,因为换个角度就能看到遮挡区域。
为了避免上述三种点被当作特征点:要求采集点
i
i
i 的激光束与
S
\mathcal S
S 的表面法向量的夹角必须大于 10°;
S
\mathcal S
S 内的点不能被障碍物阻断,如图 4(b) 的 D 点。
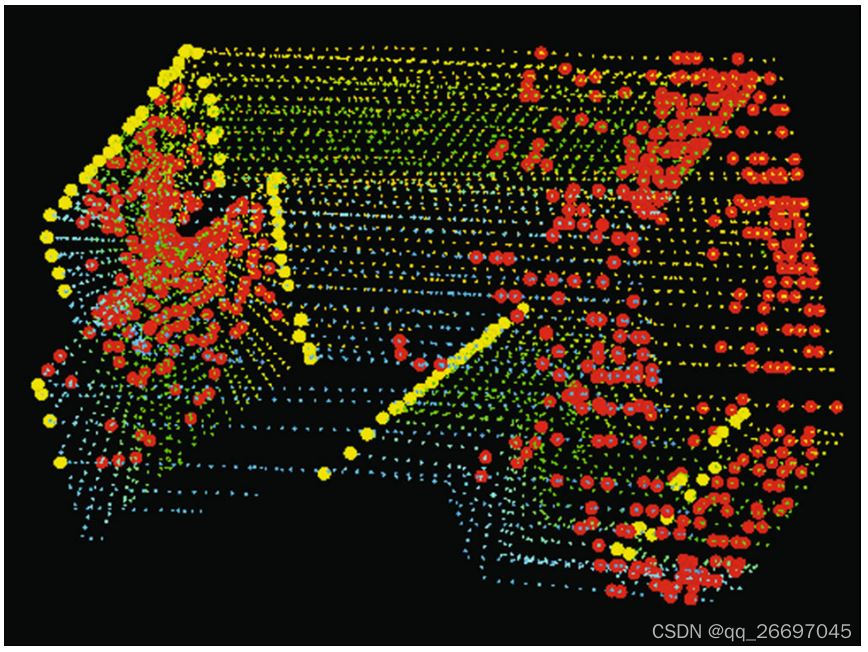
图 5 是在一个走廊场景中提取的特征点。黄色代表边缘点,红色代表平面点。激光雷达以 0.5 米每秒的速度向图左侧的墙移动,造成墙上出现运动畸变。
3. 特征点匹配
里程计算法用于估计激光雷达在一个扫描内的运动。第
k
−
1
k-1
k−1 次扫描采集到的点云
P
k
−
1
\mathcal P_{k-1}
Pk−1 会被投影到时刻
t
k
t_k
tk 得到
P
ˉ
k
−
1
\bar \mathcal P_{k-1}
Pˉk−1,从
P
k
\mathcal P_k
Pk 中提取的特征点也会被投影到时刻
t
k
t_k
tk。投影后的点用于估计雷达的运动。
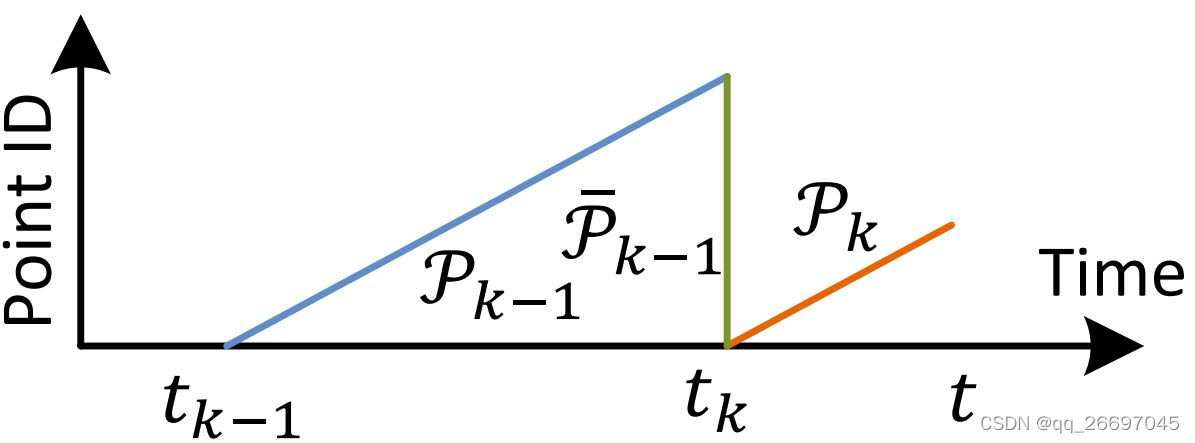
图 6 中,蓝色的线表示的第 k − 1 k-1 k−1 次扫描采集到的点云 P k − 1 \mathcal P_{k-1} Pk−1。在第 k − 1 k-1 k−1 次扫描的结束时刻 t k t_k tk, P k − 1 \mathcal P_{k-1} Pk−1 被投影到时刻 t k t_k tk,投影后用 P ˉ k − 1 \bar \mathcal P_{k-1} Pˉk−1 表示,如图中的绿线。在第 k k k 次扫描过程中, P ˉ k − 1 \bar \mathcal P_{k-1} Pˉk−1 和新采集到的点云 P k \mathcal P_k Pk(黄线)一起用于估计激光雷达的运动。
特征点匹配时,先使用前面讨论的特征点提取算法从 P k \mathcal P_k Pk 中提取边缘点 E k \mathcal E_k Ek 和平面点 H k \mathcal H_k Hk。再从 P ˉ k − 1 \bar \mathcal P_{k-1} Pˉk−1 中选择边缘线和平面块作为边缘点和平面点的匹配。
注意, P k \mathcal P_k Pk 在第 k k k 次扫描开始时是空的,它包含的点云数量随着扫描逐渐增长。里程计在采集过程中递归地估计激光雷达的 6 自由度运动。 E k \mathcal E_k Ek 和 H k \mathcal H_k Hk 被投影到扫描开始时刻,得到 E ~ k \tilde \mathcal E_k E~k 和 H ~ k \tilde \mathcal H_k H~k。我们需要在 P ˉ k − 1 \bar \mathcal P_{k-1} Pˉk−1 中为 E ~ k \tilde \mathcal E_k E~k 和 H ~ k \tilde \mathcal H_k H~k 中的每一个特征点找到最近点。为了快速查找, P ˉ k − 1 \bar \mathcal P_{k-1} Pˉk−1 以三维 KD 树的形式存储,存储的形式是 L k L_k Lk。
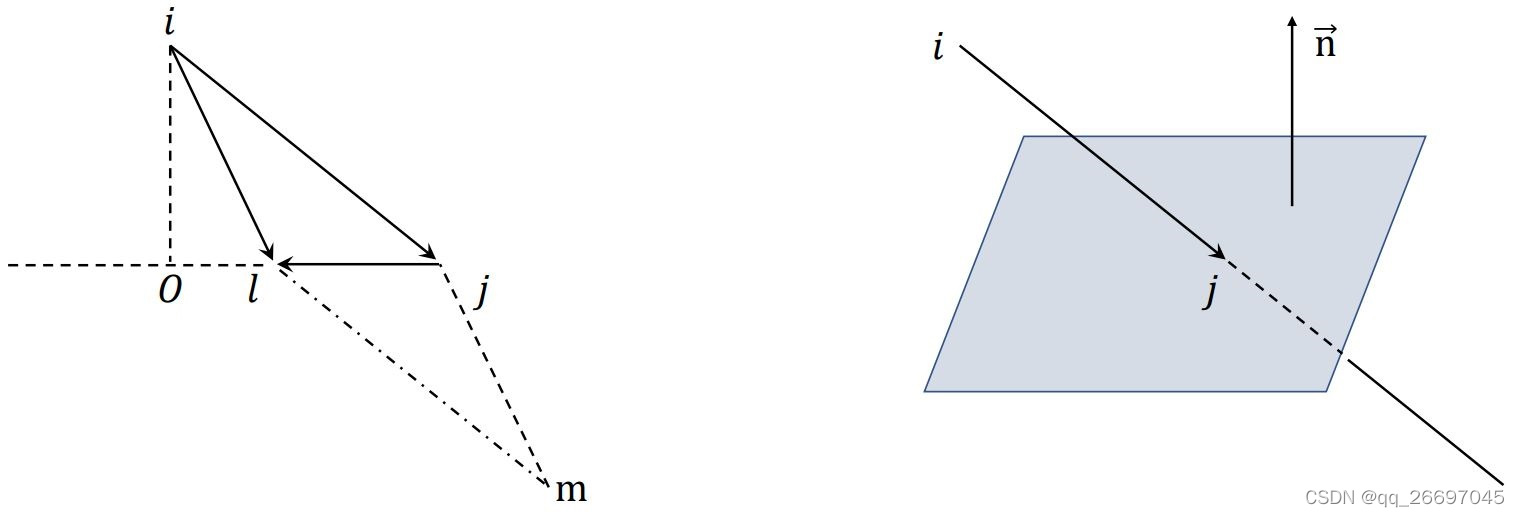
图 7(a) 是为一个边缘点匹配一个边缘线的过程。边缘线由来自 P ˉ k − 1 \bar \mathcal P_{k-1} Pˉk−1 的两个点 j j j、 l l l 表示。假设 i i i 是 E ~ k \tilde \mathcal E_k E~k 中的一点, j j j 是 P ˉ k − 1 \bar \mathcal P_{k-1} Pˉk−1 中离 i i i 最近的点, l l l 是 P ˉ k − 1 \bar \mathcal P_{k-1} Pˉk−1 中与 j j j 相邻的两行中离 i i i 最近的点。于是,边缘线 ( j , l ) (j, l) (j,l) 就是边缘点 i i i 的匹配。然后使用公式 (1) 验证 j j j 和 l l l 是边缘点,要求 c > 5 × 1 0 − 3 c \gt 5 \times 10^{-3} c>5×10−3。
之所以要求 j j j 和 l l l 来自不同的扫描行,是考虑到一次扫描不能从同一条边缘线采集到两个及以上的点,除非边缘线在扫描平面上。如果边缘线在扫描平面上,它就退化成一条直线,这条线上的特征点一开始也就不会被当成特征点。
图 7(b) 是为一个平面点匹配一个平面块的过程。平面块由来自
P
ˉ
k
−
1
\bar \mathcal P_{k-1}
Pˉk−1 的三个点
j
j
j、
l
l
l、
m
m
m 表示。假设
i
i
i 是
H
k
\mathcal H_k
Hk 中的一点,
j
j
j 是
P
ˉ
k
−
1
\bar \mathcal P_{k-1}
Pˉk−1 中离
i
i
i 最近的点,
l
l
l 是
P
ˉ
k
−
1
\bar \mathcal P_{k-1}
Pˉk−1 中与
j
j
j 同行且离
i
i
i 第二近的点,
m
m
m 是来自
j
j
j 旁边两行离
i
i
i 最近的点。这样可以保证三个点不共线。然后使用公式 (1) 验证
j
j
j、
l
l
l、
m
m
m 都是平面点,要求
c
<
5
×
1
0
−
3
c \lt 5 \times 10^{-3}
c<5×10−3。
图 7(a) 表示为 E ~ k \tilde \mathcal E_k E~k 中的一个边缘点 i i i 匹配边缘线,图 7(b) 表示为 H ~ k \tilde \mathcal H_k H~k 中的一个平面点 i i i 匹配平面块。 j j j 是从 P ˉ k − 1 \bar \mathcal P_{k-1} Pˉk−1 中找到的离 i i i 最近的点。橘色线代表的点和 j j j 来自同一行扫描,蓝色线代表橘色线前后的两行扫描。在图 a 中,为了找到边缘线,在蓝色线中寻找点 l l l。在图 b 中,为了找到平面块,分别在橘色线和蓝色线中寻找点 l l l 和点 m m m。
接下来计算特征点到它的匹配对象的距离,然后最小化所有距离求得激光雷达的运动。
E ~ k \tilde \mathcal E_k E~k 中的一点 i i i 到直线 ( j , l ) (j, l) (j,l) 的距离
d E = ∣ ( X ~ ( k , i ) L − X ˉ ( k − 1 , j ) L ) × ( X ~ ( k , i ) L − X ˉ ( k − 1 , l ) L ) ∣ ∣ X ˉ ( k − 1 , j ) L − X ˉ ( k − 1 , l ) L ∣ , (2) d_{\mathcal E} = \frac {\left|\begin{array}{cccc} (\tilde X_{(k, i)}^L - \bar X_{(k-1, j)}^L) \times (\tilde X_{(k, i)}^L - \bar X_{(k-1, l)}^L) \end{array}\right|} {\left|\begin{array}{cccc} \bar X_{(k-1, j)}^L - \bar X_{(k-1, l)}^L \end{array}\right|}, \tag{2} dE=∣∣∣Xˉ(k−1,j)L−Xˉ(k−1,l)L∣∣∣∣∣∣(X~(k,i)L−Xˉ(k−1,j)L)×(X~(k,i)L−Xˉ(k−1,l)L)∣∣∣,(2)
其中 X ~ ( k , i ) L \tilde X_{(k, i)}^L X~(k,i)L、 X ˉ ( k − 1 , j ) L \bar X_{(k-1, j)}^L Xˉ(k−1,j)L、 X ˉ ( k − 1 , l ) L \bar X_{(k-1, l)}^L Xˉ(k−1,l)L 分别是 i i i、 j j j、 l l l 在坐标系 L k L_k Lk 中的坐标。 H ~ k \tilde \mathcal H_k H~k 中的一点 i i i 到平面 ( j , l , m ) (j, l, m) (j,l,m) 的距离
d H = ∣ X ~ ( k , i ) L − X ˉ ( k − 1 , j ) L ( X ˉ ( k − 1 , j ) L − X ˉ ( k − 1 , l ) L ) × ( X ˉ ( k − 1 , j ) L − X ˉ ( k − 1 , m ) L ) ∣ ∣ ( X ˉ ( k − 1 , j ) L − X ˉ ( k − 1 , l ) L ) × ( X ˉ ( k − 1 , j ) L − X ˉ ( k − 1 , m ) L ) ∣ . (3) d_{\mathcal H} = \frac {\left|\begin{array}{cccc} \tilde X_{(k, i)}^L - \bar X_{(k-1, j)}^L\\ (\bar X_{(k-1, j)}^L - \bar X_{(k-1, l)}^L) \times (\bar X_{(k-1, j)}^L - \bar X_{(k-1, m)}^L) \end{array}\right|} {\left|\begin{array}{cccc} (\bar X_{(k-1, j)}^L - \bar X_{(k-1, l)}^L) \times (\bar X_{(k-1, j)}^L - \bar X_{(k-1, m)}^L) \end{array}\right|}. \tag{3} dH=∣∣∣(Xˉ(k−1,j)L−Xˉ(k−1,l)L)×(Xˉ(k−1,j)L−Xˉ(k−1,m)L)∣∣∣∣∣∣∣∣X~(k,i)L−Xˉ(k−1,j)L(Xˉ(k−1,j)L−Xˉ(k−1,l)L)×(Xˉ(k−1,j)L−Xˉ(k−1,m)L)∣∣∣∣∣.(3)
公式 (2) 和公式 (3) 的推导分别参见附录 8.2 和 8.3。
4. 运动估计
激光雷达在一个扫描覆盖内的运动被建模为角速度和线速度都是匀速的运动,这样就可以根据时间戳使用线性插值的方式求得一个扫描内各时刻的位姿。假设 t k t_k tk 是第 k k k 次扫描覆盖的开始时刻, t t t 是当前时刻。 T k L ( t ) \boldsymbol T_k^L(t) TkL(t) 是雷达从时刻 t t t 变换回时刻 t k t_k tk 的六自由度位姿变换, T k L ( t ) = [ τ k L ( t ) , θ k L ( t ) ] T \boldsymbol T_k^L(t) = [\tau_k^L(t), \theta_k^L(t)]^T TkL(t)=[τkL(t),θkL(t)]T,其中 τ k L ( t ) = [ t x , t y , t z ] T \tau_k^L(t) = [t_x, t_y, t_z]^T τkL(t)=[tx,ty,tz]T 和 θ k L ( t ) = [ θ x , θ y , θ z ] T \theta_k^L(t) = [\theta_x, \theta_y, \theta_z]^T θkL(t)=[θx,θy,θz]T 分别是在 L k L_k Lk 坐标系中的平移和旋转。给定 θ k L ( t ) \theta_k^L(t) θkL(t),旋转矩阵可以根据罗德里格斯(Rodrigues)公式定义为
R k L ( t ) = e θ ^ k L ( t ) = I + θ ^ k L ( t ) ∣ ∣ θ k L ( t ) ∣ ∣ s i n ∣ ∣ θ k L ( t ) ∣ ∣ + ( θ ^ k L ( t ) ∣ ∣ θ k L ( t ) ∣ ∣ ) 2 ( 1 − ∣ ∣ c o s θ k L ( t ) ∣ ∣ ) . (4) {\bf R}_k^L(t) = e^{\hat \theta_k^L(t)} = {\bf I} + \frac{\hat \theta_k^L(t)}{|| \theta_k^L(t) ||} sin|| \theta_k^L(t) || + (\frac{\hat \theta_k^L(t)}{|| \theta_k^L(t) ||})^2 (1 - || cos\theta_k^L(t) ||). \tag{4} RkL(t)=eθ^kL(t)=I+∣∣θkL(t)∣∣θ^kL(t)sin∣∣θkL(t)∣∣+(∣∣θkL(t)∣∣θ^kL(t))2(1−∣∣cosθkL(t)∣∣).(4)
其中, θ ^ k L ( t ) \hat \theta_k^L(t) θ^kL(t) 是 θ k L ( t ) \theta_k^L(t) θkL(t) 的斜对称矩阵。
假设 i i i 是 P k \mathcal P_k Pk 中的一点, t ( k , i ) t(k, i) t(k,i) 是它的时间戳, T ( k , i ) L \boldsymbol T_{(k, i)}^L T(k,i)L 是 [ t k , t ( k , i ) ] [t_k, t_{(k, i)}] [tk,t(k,i)] 间某个时刻的位姿变换。 T ( k , i ) L \boldsymbol T_{(k, i)}^L T(k,i)L 可以通过对 T k L ( t ) \boldsymbol T_k^L(t) TkL(t) 线性插值计算得到:
T ( k , i ) L = t ( k , i ) − t k t − t k T k L ( t ) . (5) \boldsymbol T_{(k, i)}^L = \frac{t_{(k, i)} - t_k}{t - t_k} \boldsymbol T_k^L(t). \tag{5} T(k,i)L=t−tkt(k,i)−tkTkL(t).(5)
注意, T k L ( t ) \boldsymbol T_k^L(t) TkL(t) 随着时间变化,所以上面的插值也随着时间的变化而不同。下面的公式把边缘点 E k \mathcal E_k Ek 和平面点 H k \mathcal H_k Hk 变换到扫描的开始时刻,得到 E ~ k \tilde \mathcal E_k E~k 和平面点 H ~ k \tilde \mathcal H_k H~k:
X ~ ( k , i ) L = R ( k , i ) L X ( k , i ) L + τ ( k , i ) L , (6) {\boldsymbol {\tilde X}}_{(k, i)}^L = {\bf R}_{(k, i)}^L {\boldsymbol X}_{(k, i)}^L + \tau_{(k, i)}^L, \tag{6} X~(k,i)L=R(k,i)LX(k,i)L+τ(k,i)L,(6)
其中, X ( k , i ) L {\boldsymbol X}_{(k, i)}^L X(k,i)L 是 E k \mathcal E_k Ek 或 H k \mathcal H_k Hk 中的一点, X ~ ( k , i ) L {\boldsymbol {\tilde X}}_{(k, i)}^L X~(k,i)L 是 X ( k , i ) L {\boldsymbol X}_{(k, i)}^L X(k,i)L 变换后的点。 R ( k , i ) L {\bf R}_{(k, i)}^L R(k,i)L 和 τ ( k , i ) L \tau_{(k, i)}^L τ(k,i)L 是 T ( k , i ) L {\boldsymbol T}_{(k, i)}^L T(k,i)L 包含的旋转矩阵和平移向量。
公式(2)用于计算投影后的点到其匹配对象的距离,公式(6)定义投影操作。把这两个公式合写成一个公式:
f E ( X ( k , i ) L , T k L ( t ) ) = d E , i ∈ E k . (7) f_{\mathcal E} ({\boldsymbol X}_{(k, i)}^L, {\boldsymbol T}_k^L(t)) = d_{\mathcal E}, \quad i \in {\mathcal E}_k. \tag{7} fE(X(k,i)L,TkL(t))=dE,i∈Ek.(7)
该公式把一个边缘点 X ( k , i ) L {\boldsymbol X}_{(k, i)}^L X(k,i)L 投影到时刻 t k t_k tk,并求投影后的点到与其匹配的边缘线的距离 d E d_{\mathcal E} dE。同样,由公式 (3) 和公式 (6) 可以得到 H k \mathcal H_k Hk 中的一个平面点到与其匹配的平面块的距离:
f H ( X ( k , i ) L , T k L ( t ) ) = d H , i ∈ H k . (8) f_{\mathcal H} ({\boldsymbol X}_{(k, i)}^L, {\boldsymbol T}_k^L(t)) = d_{\mathcal H}, \quad i \in {\mathcal H}_k. \tag{8} fH(X(k,i)L,TkL(t))=dH,i∈Hk.(8)
最后使用莱文贝格-马夸特(Levenberg–Marquardt)算法求解激光雷达的运动。把公式 (7) 和 (8) 写成一个统一的形式,就得到一个非线性函数:
f ( T k L ( t ) ) = d , (9) \boldsymbol { f(T_k^L(t)) = d }, \tag{9} f(TkL(t))=d,(9)
其中, f \boldsymbol f f 的每行对应一个特征点, d \boldsymbol d d 是相应的距离。我们计算 f \boldsymbol f f 关于 T k L ( t ) \boldsymbol T_k^L(t) TkL(t) 的雅可比矩阵 J \bf J J,其中 J = ∂ f / ∂ T k L ( t ) {\bf J} = \partial f / \partial {\boldsymbol T}_k^L(t) J=∂f/∂TkL(t)。然后使用非线性迭代最小化 d \boldsymbol d d 就可以求解公式 (9):
T k L ( t ) ← T k L ( t ) − ( J T J + λ d i a g ( J T J ) ) − 1 J T d . (10) {\boldsymbol T}_k^L(t) \leftarrow {\boldsymbol T}_k^L(t) - ({\bf J}^T{\bf J} + \lambda diag({\bf J}^T{\bf J}))^{-1} {\bf J}^T{\boldsymbol d}. \tag{10} TkL(t)←TkL(t)−(JTJ+λdiag(JTJ))−1JTd.(10)
其中 λ \lambda λ 是莱文贝格-马夸特算法需要的一个因数。
5. 里程计算法
下面是第 k k k 次扫描覆盖过程中,里程计算法的迭代过程。它的输入有三个:
- P ˉ k − 1 \bar \mathcal P_{k-1} Pˉk−1: 第 k − 1 k-1 k−1 次扫描覆盖采集到的点 P k − 1 \mathcal P_{k-1} Pk−1 在时刻 t k t_k tk 的投影。
- P k \mathcal P_k Pk: 从时刻 t k t_k tk 到时刻 t t t 期间采集到的点,点的数量随着 t t t 的增大而增多。
- T k L ( t ) \boldsymbol T_k^L(t) TkL(t): 时刻 t t t 到时刻 t k t_k tk 的变换,其中 t k ≤ t ≤ t k + 1 t_k \le t \le t_{k+1} tk≤t≤tk+1。该算法在时间段 [ t k , t k + 1 ] [t_k, t_{k+1}] [tk,tk+1] 中迭代: T k L ( t ) \boldsymbol T_k^L(t) TkL(t) 在 t k t_k tk 时刻被赋予初始值 0,然后在每次迭代过程中更新,在 t k + 1 t_{k+1} tk+1 时刻迭代结束即为时刻 t k + 1 t_{k+1} tk+1 到时刻 t k t_k tk 的变换。
T k L ( t ) \boldsymbol T_k^L(t) TkL(t) 的初始值为 0。从第二次迭代开始, T k L ( t ) \boldsymbol T_k^L(t) TkL(t) 使用上次迭代结束时它的值。 T k L ( t ) \boldsymbol T_k^L(t) TkL(t) 的更新方法:
- 从 P k \mathcal P_k Pk 中选择特征点 E k \mathcal E_k Ek 和 H k \mathcal H_k Hk。
- 使用 T k L ( t ) \boldsymbol T_k^L(t) TkL(t) 把它们变换到 t k t_k tk 时刻,得到 E ~ k \tilde \mathcal E_k E~k 和 H ~ k \tilde \mathcal H_k H~k。
- 假设 i i i 是 E ~ k \tilde \mathcal E_k E~k 或 H ~ k \tilde \mathcal H_k H~k 中的一个点。在 P ˉ k − 1 \bar \mathcal P_{k-1} Pˉk−1 中找 i i i 的匹配对象边缘线或平面块,计算 i i i 到该匹配对象的距离。调整 T k L ( t ) \boldsymbol T_k^L(t) TkL(t) 使距离总和减小,此时的 T k L ( t ) \boldsymbol T_k^L(t) TkL(t) 即为本次迭代的结果。
当距离总和收敛或达到最大迭代次数时停止迭代。由于里程计的频率是 10 赫兹,所以距离该算法上次被调用的时间达到 100 毫秒时,该算法再次被调用。因为在这 100 毫秒中, P k \mathcal P_k Pk 中又增加了一些点。
为了区分特征匹配的质量,为每个距离添加一个权重:特征点和它的匹配对象间的距离越大,权重越小;距离大于阈值,权重为 0。权重的定义如下:
w = { ( 1 − α 2 ) 2 − 1 < α < 1 , 0 o t h e r w i s e , (11) w = \left\{ \begin{matrix} (1 - \alpha^2)^2 & -1 \lt \alpha \lt 1, \\ 0 & otherwise, \end{matrix} \right. \tag{11} w={(1−α2)20−1<α<1,otherwise,(11)
其中 α = r 6.9459 σ 1 − h \alpha = \frac{r}{6.9459 \sigma \sqrt{1 - h}} α=6.9459σ1−hr, r r r 是最小二乘对应的残差, σ \sigma σ 是残差的中位数绝对离差, h h h 是 ( J ( J T J ) ) − 1 J T ({\bf J}({\bf J}^{\boldsymbol T} {\bf J}))^{-1}{\bf J}^T (J(JTJ))−1JT 对角线上的杠杆值或对应元, J \bf J J 是公式 (10) 中说过的雅可比矩阵。
6. 地图创建算法
第
k
k
k 次扫描覆盖结束时,里程计算法计算出一个位姿变换
T
k
L
(
t
)
\boldsymbol T_k^L(t)
TkL(t),其中
t
=
t
k
+
1
t=t_{k+1}
t=tk+1。该变换可以祛除
P
k
\mathcal P_k
Pk 中的畸变得到
P
ˉ
k
\bar \mathcal P_k
Pˉk。
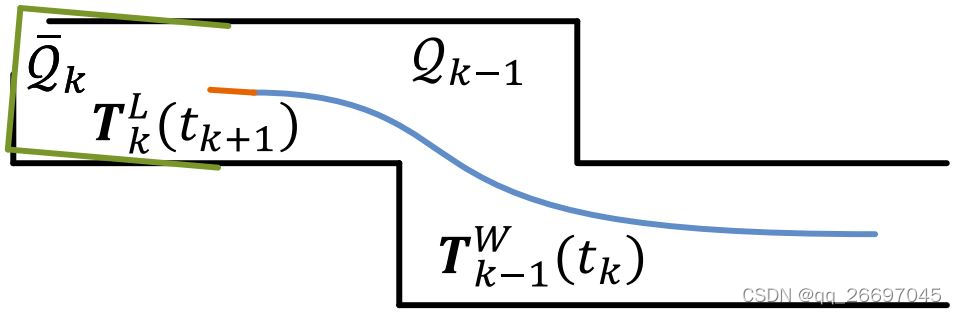
蓝色曲线代表雷达在地图中的位姿 T k − 1 W ( t k ) \boldsymbol T_{k-1}^W(t_k) Tk−1W(tk),该位姿是地图创建算法在第 k − 1 k-1 k−1 次扫描周期内计算出来的。橘色曲线代表雷达在第 k k k 次扫描过程中的运动 T k L ( t k + 1 ) \boldsymbol T_k^L(t_{k+1}) TkL(tk+1),该运动是里程计算法计算出来的。根据 T k − 1 W ( t k ) \boldsymbol T_{k-1}^W(t_k) Tk−1W(tk) 和 T k L ( t k + 1 ) \boldsymbol T_k^L(t_{k+1}) TkL(tk+1),里程计算法产生的无畸变点云被投影到地图中成为 Q k \mathcal Q_k Qk(绿线),并与地图中存在的点云 Q k − 1 \mathcal Q_{k-1} Qk−1 (黑线)匹配。
地图创建算法在每个扫描周期内仅被调用一次,它把 P ˉ k \bar \mathcal P_k Pˉk 与地图匹配并注册 P ˉ k \bar \mathcal P_k Pˉk 到世界坐标系 { W } \{W\} {W} 中,如图 8 所示。
定义 Q k − 1 \mathcal Q_{k-1} Qk−1 是截至第 k − 1 k-1 k−1 次扫描结束时,地图中积累的点云; T k − 1 W ( t k ) \boldsymbol T_{k-1}^W(t_k) Tk−1W(tk) 是第 k − 1 k-1 k−1 次扫描结束时刻 t k t_k tk,雷达在地图中的位姿。地图创建算法把 T k − 1 W ( t k ) \boldsymbol T_{k-1}^W(t_k) Tk−1W(tk) 扩展到 [ t k , t k + 1 ] [t_k, t_{k+1}] [tk,tk+1] 得到 T k W ( t k + 1 ) \boldsymbol T_k^W(t_{k+1}) TkW(tk+1),把 P ˉ k \bar \mathcal P_k Pˉk 投影到世界坐标系 { W } \{W\} {W} 得到 Q ˉ k \bar \mathcal Q_k Qˉk,然后通过优化雷达位姿 T k W ( t k + 1 ) \boldsymbol T_k^W(t_{k+1}) TkW(tk+1) 匹配 Q ˉ k \bar \mathcal Q_k Qˉk 和 Q k − 1 \mathcal Q_{k-1} Qk−1。
为了寻找特征点的匹配对象,把地图 Q k − 1 \mathcal Q_{k-1} Qk−1 中的点云储存在一个 10 立方米的区域内。这个区域与 Q ˉ k \bar \mathcal Q_k Qˉk 重叠的部分中的点会按它们在世界坐标系 W {W} W 中的坐标被存储在一个三维 KD 树中。假设 S ′ \mathcal S' S′ 是 Q k − 1 \mathcal Q_{k-1} Qk−1 中,以特征点为中心的一个棱长为 10 厘米的立方体区域。对于一个边缘点,只保留 S ′ \mathcal S' S′ 中边缘线上的点;对于一个平面点,只保留 S ′ \mathcal S' S′ 中平面块上的点。然后计算 S ′ \mathcal S' S′ 的协方差矩阵 M \bf M M 及 M \bf M M 的特征值 V \boldsymbol V V 和特征向量 E \boldsymbol E E。这些值决定点云簇的位姿和点线、点面距离。
如果 S ′ \mathcal S' S′ 位于边缘线上, V \boldsymbol V V 的一个特征值会明显大于另外两个,最大的一个特征值对应的特征向量代表着边缘线的方向。如果 S ′ \mathcal S' S′ 位于平面块上, V \boldsymbol V V 的一个特征值会明显小于另外两个,最小的一个特征值对应的特征向量代表着平面块的方向。这样计算的边缘线和平面块经过 S ′ \mathcal S' S′ 的中心。
为了计算特征点到其匹配对象的距离,在边缘线上选择两个点,在平面块上选择三个点,然后使用公式(2)和公式(3)计算距离。然后使用公式(7)和公式(8)计算距离。不同的是, Q ˉ k \bar \mathcal Q_k Qˉk 中的点时间戳都是 t k + 1 t_{k+1} tk+1。再次使用莱文贝格-马夸特算法进行非线性优化,接着 Q ˉ k \bar \mathcal Q_k Qˉk 被注册到地图。
为了分布均匀,每次把一次扫描合并到地图后,都使用体素网格滤波器对地图点云下采样。体素网格滤波器使各体素中包含相同数量的点。边缘点和平面点的体素尺寸不同,前者的体素棱长为 5 厘米,后者的体素棱长为 10 厘米。为了限制内存占用,地图大小被限制在以传感器为中心,棱长为 500 米的范围内。
蓝色区域代表地图创建算法在每个扫描周期内计算出的一个位姿 T k − 1 W ( t k ) \boldsymbol T_{k-1}^W(t_k) Tk−1W(tk)。橘色区域代表里程计以 10 赫兹的频率计算出的雷达在当前扫描过程中的运动。雷达的运动估计包含两个变换,频率也是 10 赫兹。
位姿变换如图 9。蓝色区域代表地图创建算法在每个扫描周期内计算出的一个位姿 T k − 1 W ( t k ) \boldsymbol T_{k-1}^W(t_k) Tk−1W(tk)。橘色区域代表里程计以 10 赫兹的频率计算出的变换 T k L ( t ) \boldsymbol T_k^L(t) TkL(t)。雷达相对地图的位姿包含这两个变换,频率也是 10 赫兹。
7. 附录
7.1 数量积与向量积
数量积又称点积、内积,计算方式为:
a ⃗ ⋅ b ⃗ = { x 1 x 2 + y 1 y 2 ∣ a ⃗ ∣ ∣ b ⃗ ∣ c o s θ . (8.1) \vec{a} \cdot \vec{b} = \begin{cases} x_1x_2 + y_1y_2 \\ |\vec{a}||\vec{b}|cos\theta \end{cases}. \tag{8.1} a⋅b={x1x2+y1y2∣a∣∣b∣cosθ.(8.1)
如果知道平面的法向量和平面上一点,由第二个公式可以求得平面外一点到平面的距离。
向量积又称叉积、外积,计算方式为:
{ a ⃗ × b ⃗ = ( a y b z − a z b y ) i ⃗ + ( a z b x − a x b z ) j ⃗ + ( a x b y − a y b x ) k ⃗ ∣ a ⃗ × b ⃗ ∣ = ∣ a ⃗ ∣ ∣ b ⃗ ∣ s i n θ . (8.2) \begin{cases} \vec{a} \times \vec{b} = (a_yb_z - a_zb_y)\vec{i} + (a_zb_x - a_xb_z)\vec{j} + (a_xb_y - a_yb_x)\vec{k} \\ |\vec{a} \times \vec{b}| = |\vec{a}| |\vec{b}| sin\theta \end{cases}. \tag{8.2} {a×b=(aybz−azby)i+(azbx−axbz)j+(axby−aybx)k∣a×b∣=∣a∣∣b∣sinθ.(8.2)
第一个公式求得的是一个垂直于向量 a ⃗ \vec{a} a 和 b ⃗ \vec{b} b 所在平面的向量。第二个公式求得的是以 a ⃗ \vec{a} a 和 b ⃗ \vec{b} b 为邻边的平行四边形的面积。
7.2 点到直线的距离
我们讨论向量形式的点到直线距离公式。如图 8.1(左),点
i
i
i 是直线
j
l
jl
jl 外一点,
i
i
i、
j
j
j、
l
l
l 坐标已知,求点
i
i
i 到直线
j
l
jl
jl 的距离。
作平行四边形 i j m l ijml ijml,则其面积是 ∣ i j ⃗ × i l ⃗ ∣ |\vec {ij} \times \vec {il}| ∣ij×il∣。因为直线 j l jl jl 把四边形分成两个全等的三角形,所以四边形的面积也等于 ∣ O i ⃗ ∣ ⋅ ∣ j l ⃗ ∣ |\vec {Oi}| \cdot |\vec {jl}| ∣Oi∣⋅∣jl∣,其中 O O O 是过点 i i i 的直线与直线 j l jl jl 的垂足。所以点 i i i 到直线 j l jl jl 的距离
∣ O i ⃗ ∣ = ∣ i j ⃗ × i l ⃗ ∣ ∣ j l ⃗ ∣ . (8.3) |\vec {Oi}| = \frac{|\vec {ij} \times \vec {il}|}{|\vec {jl}|}. \tag{8.3} ∣Oi∣=∣jl∣∣ij×il∣.(8.3)
7.3 点到平面的距离
我们讨论向量形式的点到平面距离公式。如图 7(右),已知平面上的三个点 j j j、 l l l、 m m m 和平面外一点 i i i 的坐标,求点 i i i 到平面的距离。
由平面上的三点可以求得平面的法向量 n ⃗ = j l ⃗ × j m ⃗ \vec{n} = \vec{jl} \times \vec{jm} n=jl×jm,向量 i j ⃗ \vec{ij} ij 与 n ⃗ \vec{n} n 夹角的余弦值 c o s θ = ( i j ⃗ ⋅ n ⃗ ) / ( ∣ i j ⃗ ∣ ∣ n ⃗ ∣ ) cos\theta = (\vec{ij} \cdot \vec{n}) / (|\vec{ij}| |\vec{n}|) cosθ=(ij⋅n)/(∣ij∣∣n∣)。所以点 i i i 到平面的距离
∣ O i ⃗ ∣ = ∣ i j ⃗ ∣ ∣ c o s θ ∣ = ∣ i j ⃗ ∣ ∣ i j ⃗ ⋅ n ⃗ ∣ ∣ i j ⃗ ∣ ∣ n ⃗ ∣ = ∣ i j ⃗ ⋅ n ⃗ ∣ ∣ n ⃗ ∣ = ∣ i j ⃗ ⋅ ( j l ⃗ × j m ⃗ ) ∣ ∣ j l ⃗ × j m ⃗ ∣ = ∣ i j ⃗ ∣ ∣ n ⃗ u n i t ∣ (8.4) \begin{aligned} |\vec{Oi}| = |\vec{ij}| |cos \theta| = |\vec{ij}| \frac{|\vec{ij} \cdot \vec{n}|}{|\vec{ij}| |\vec{n}|} &= \frac{|\vec{ij} \cdot \vec{n}|}{|\vec{n}|} \\ &= \frac{|\vec{ij} \cdot (\vec{jl} \times \vec{jm})|}{|\vec{jl} \times \vec{jm}|} \\ &= |\vec {ij}| |\vec n_{unit}| \end{aligned} \tag{8.4} ∣Oi∣=∣ij∣∣cosθ∣=∣ij∣∣ij∣∣n∣∣ij⋅n∣=∣n∣∣ij⋅n∣=∣jl×jm∣∣ij⋅(jl×jm)∣=∣ij∣∣nunit∣(8.4)
其中 n ⃗ u n i t \vec n_{unit} nunit 是平面的单位法向量。
7.4 协方差矩阵的特征值与特征向量
矩阵
M
3
,
n
M_{3,n}
M3,n 由
n
n
n 个三维点的坐标组成,它的协方差矩阵
C
3
,
3
C_{3,3}
C3,3 是一个三阶方阵。假设
C
3
,
3
C_{3,3}
C3,3 的三个特征值从大到小排列为
λ
1
\lambda_1
λ1、
λ
2
\lambda_2
λ2、
λ
3
\lambda_3
λ3,对应的特征向量分别为
v
⃗
1
\vec v_1
v1、
v
⃗
2
\vec v_2
v2、
v
⃗
3
\vec v_3
v3。假设
n
n
n 个三维点组成的空间区域为
Z
Z
Z。
v ⃗ 1 \vec v_1 v1 是 Z Z Z 中距离最远的两个点所在直线的方向向量, λ 1 \lambda_1 λ1 是这两个点的距离。 v ⃗ 2 \vec v_2 v2 是 Z Z Z 中垂直于 v ⃗ 1 \vec v_1 v1 方向上距离最远的两个点所在直线的方向向量, λ 2 \lambda_2 λ2 是这两个点的距离。 v ⃗ 3 \vec v_3 v3 是 Z Z Z 中垂直于 v ⃗ 1 \vec v_1 v1、 v ⃗ 2 \vec v_2 v2 方向上距离最远的两个点所在直线的方向向量, λ 3 \lambda_3 λ3 是这两个点的距离。
所以,假如这 n n n 个点分布在一条直线上, λ 1 \lambda_1 λ1 明显大于 0, λ 2 \lambda_2 λ2 和 λ 3 \lambda_3 λ3 为 0;假如这 n n n 个点分散在一个平面上, λ 1 \lambda_1 λ1 和 λ 2 \lambda_2 λ2 明显大于 0, λ 3 \lambda_3 λ3 为 0;假如这 n n n 个点不共面, λ 1 \lambda_1 λ1、 λ 2 \lambda_2 λ2 和 λ 3 \lambda_3 λ3 都明显大于 0。下面使用 numpy 计算 n n n 个三维点组成的矩阵的协方差矩阵及其特征值与特征向量。
import numpy as np
import matplotlib.pyplot as plt
import mpl_toolkits.mplot3d
def show_points(x, y, z, eigenvalues, eigenvectors):
ax = plt.subplot(projection='3d')
ax.set_title('3D points')
ax.scatter(x, y, z, c='gray')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.quiver(1, 2, 3, eigenvectors[:, 0][0], eigenvectors[:, 0][1], eigenvectors[:, 0][2], length=0.1 * eigenvalues[0],
color='r')
ax.quiver(1, 2, 3, eigenvectors[:, 1][0], eigenvectors[:, 1][1], eigenvectors[:, 1][2], length=0.1 * eigenvalues[1],
color='g')
ax.quiver(1, 2, 3, eigenvectors[:, 2][0], eigenvectors[:, 2][1], eigenvectors[:, 2][2], length=0.1 * eigenvalues[2],
color='b')
plt.show()
def get_points(points='line'):
x = np.linspace(start=-30, stop=30, num=5000)
if points == 'line':
y = np.linspace(start=-20, stop=20, num=5000)
else:
y = np.random.randint(-20, 20, 5000)
z = 3 - (4 * (x - 1) + 5 * (y - 2)) / 6.0
return x, y, z
if __name__ == '__main__':
x, y, z = get_points(points='plane')
matrix = np.vstack((x, y, z)) # shape=(3, n)
# 协方差矩阵。
covariance_matrix = np.cov(matrix) # shape=(3, 3)
# 协方差矩阵的特征值与特征向量。
eigenvalues, eigenvectors = np.linalg.eig(covariance_matrix)
# 最大的特征值。
max_eigenvalue_idx = np.argmax(eigenvalues)
# 最大的特征值对应的特征向量。
max_eigenvector = eigenvectors[:, max_eigenvalue_idx]
# 绘图。
show_points(x, y, z, eigenvalues, eigenvectors)
8. 参考
- LOAM 论文 1,CMU,2014。
- LOAM 论文 2,sci-hub,2017。
- 激光雷达笔记系列,CSDN。
- A-LOAM,HKUST-Aerial-Robotics,github。
- loam_velodyne,github。
- LeGO-LOAM,github。
- A-LOAM 建图讲解,博客园。