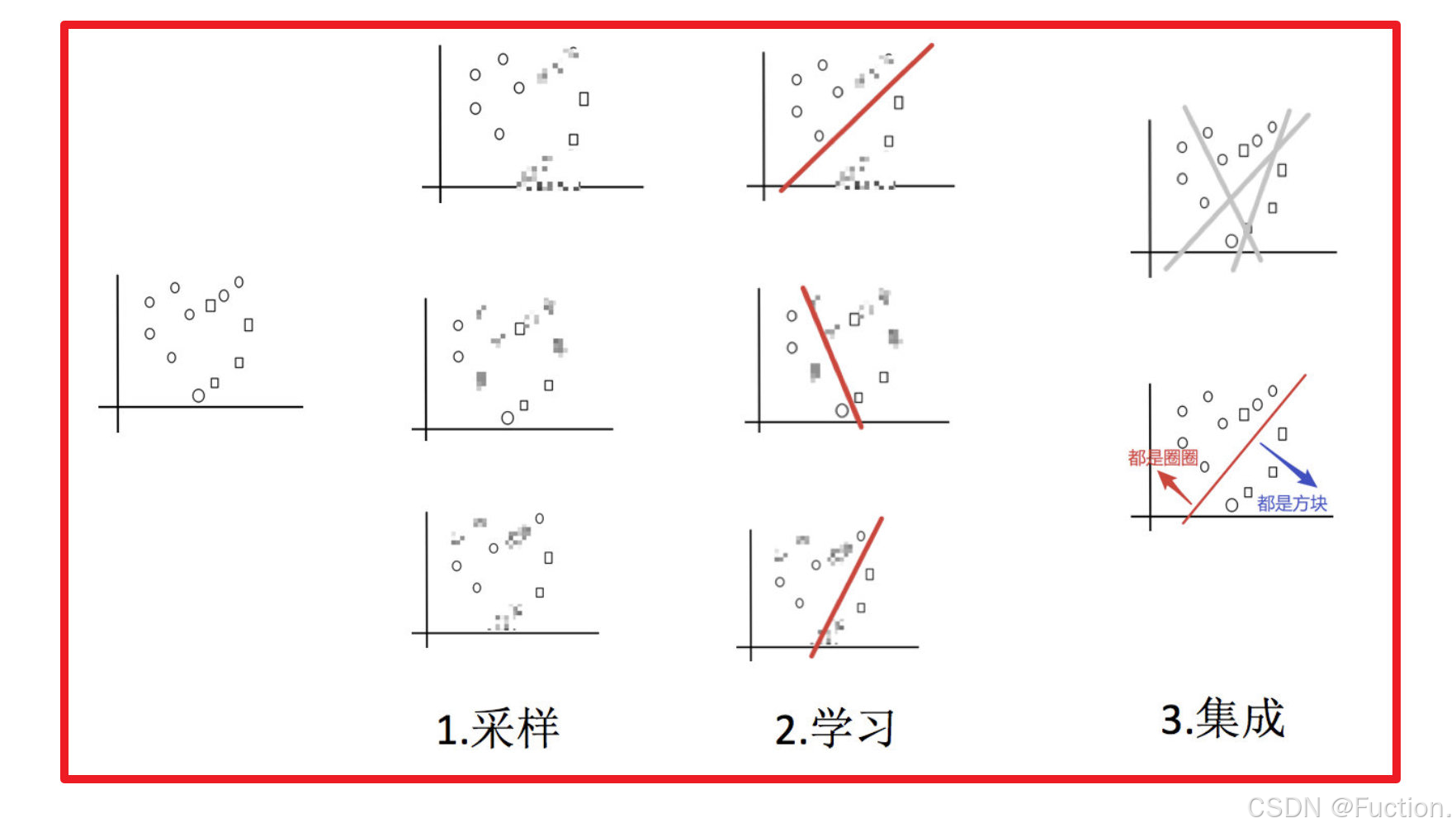
---

目标：把下面的圈和方块进行分类

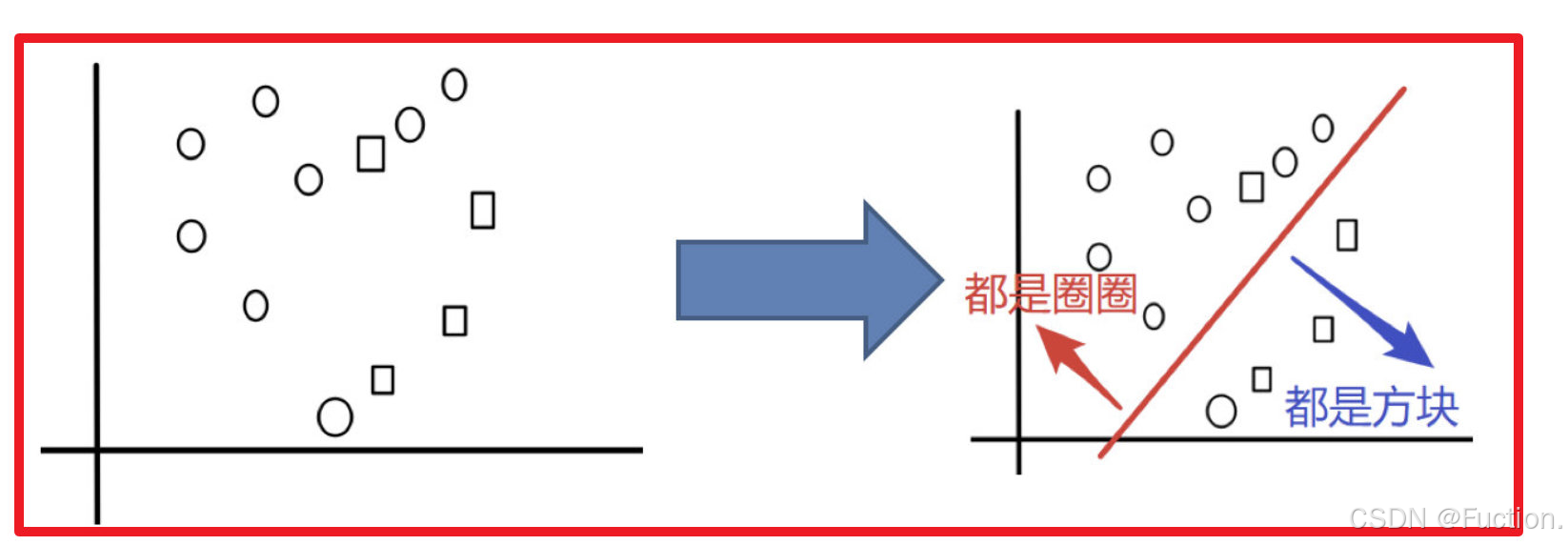
实现过程：

1) 采样不同数据集

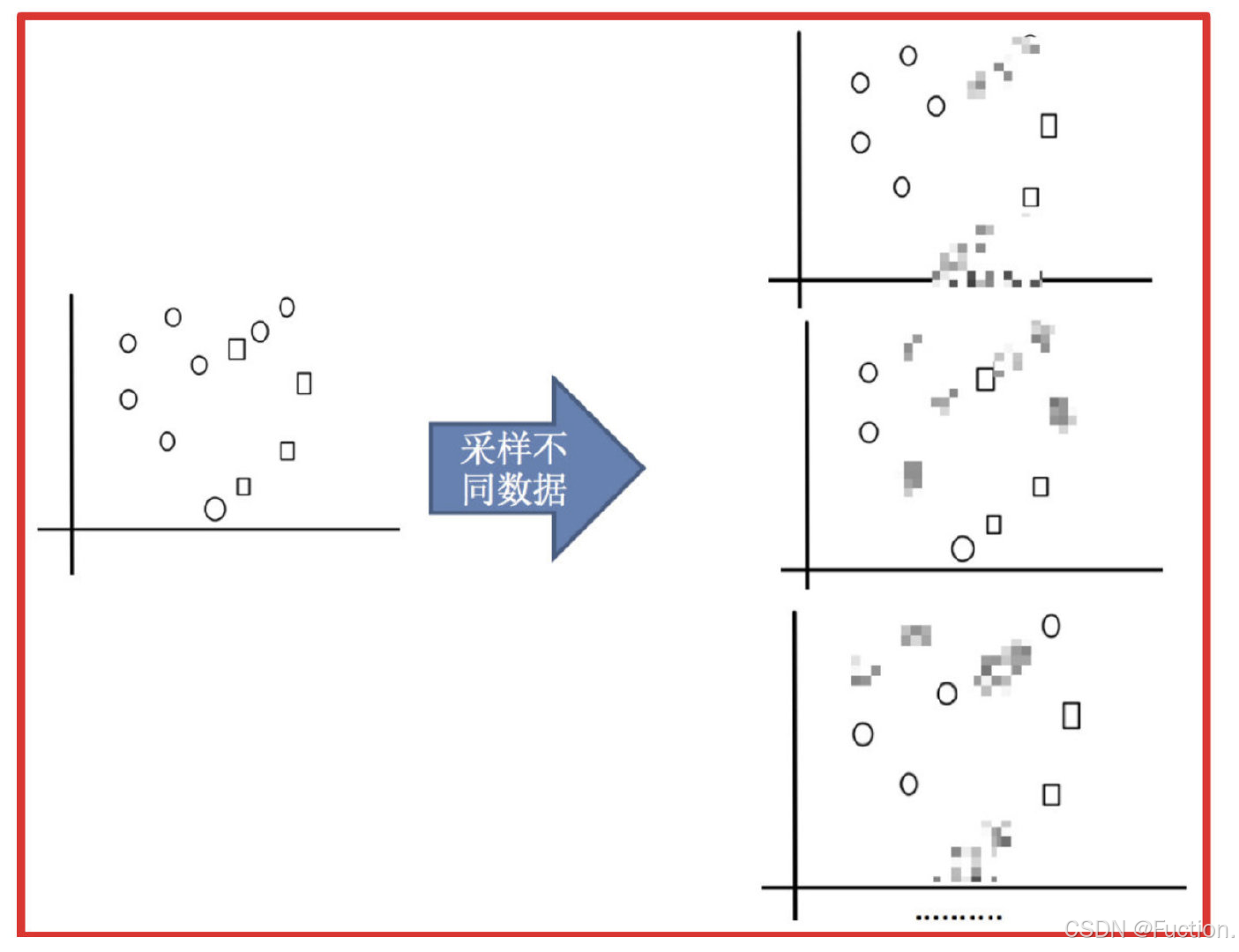
2)训练分类器

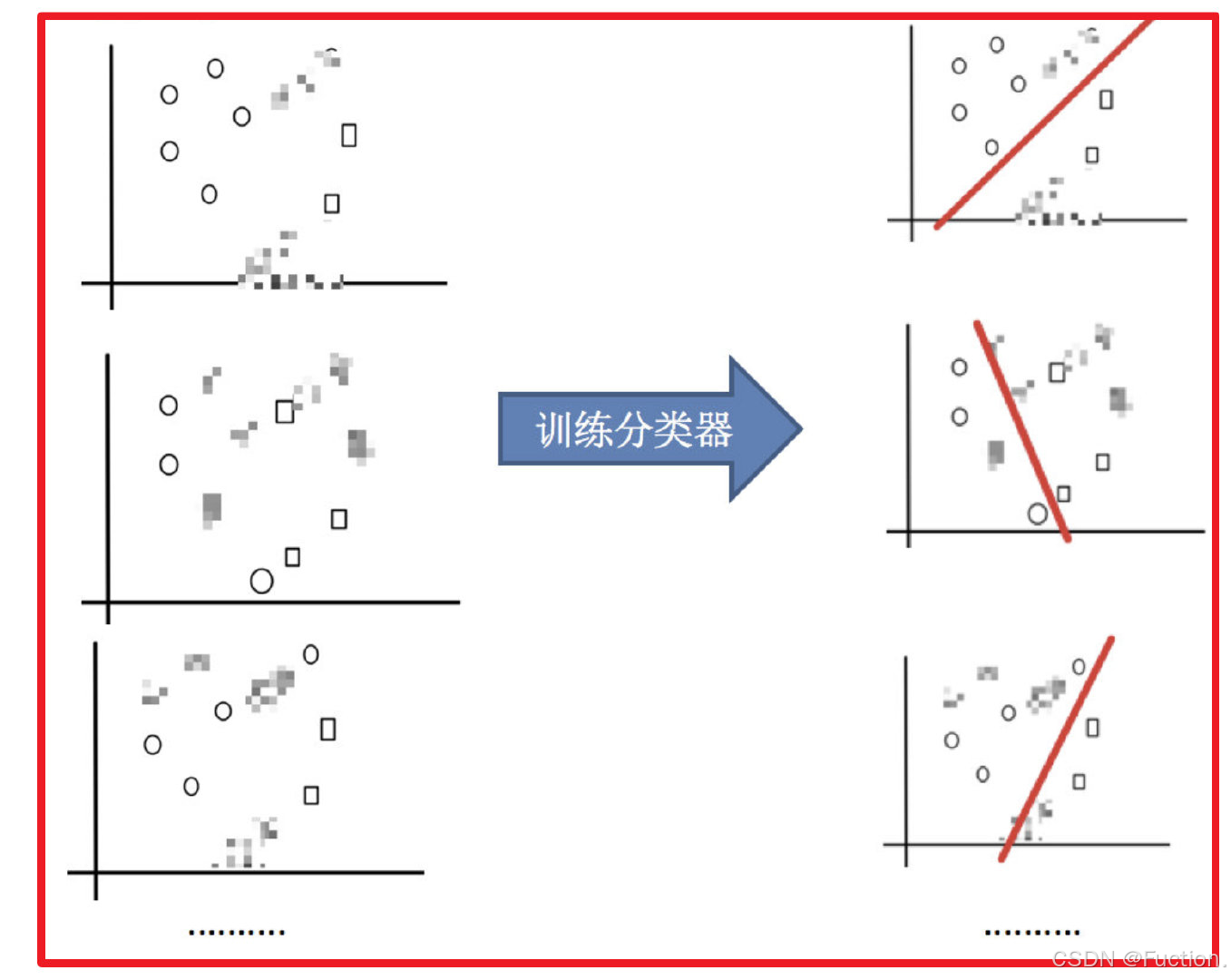
3)平权投票，获取最终结果

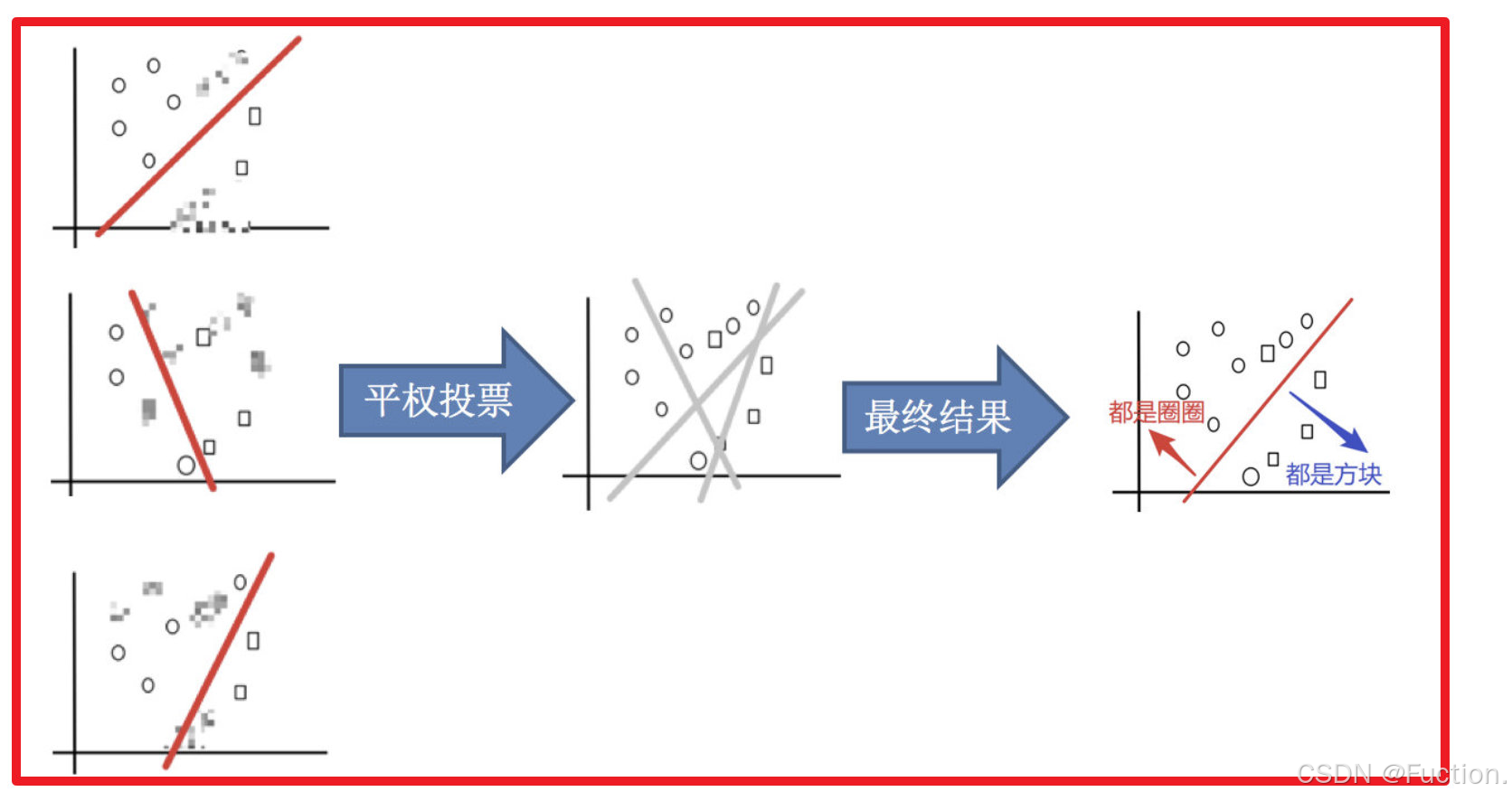
4)主要实现过程小结

在机器学习中， 随机森林是一个包含多个决策树的分类器，并且其输出的类别是由个别树输出的类别的众数而定。

随机森林  = Bagging +  决策树

例如, 如果你训练了5个树, 其中有4个树的结果是True, 1个树的结果是False, 那么最终投票结果就是True

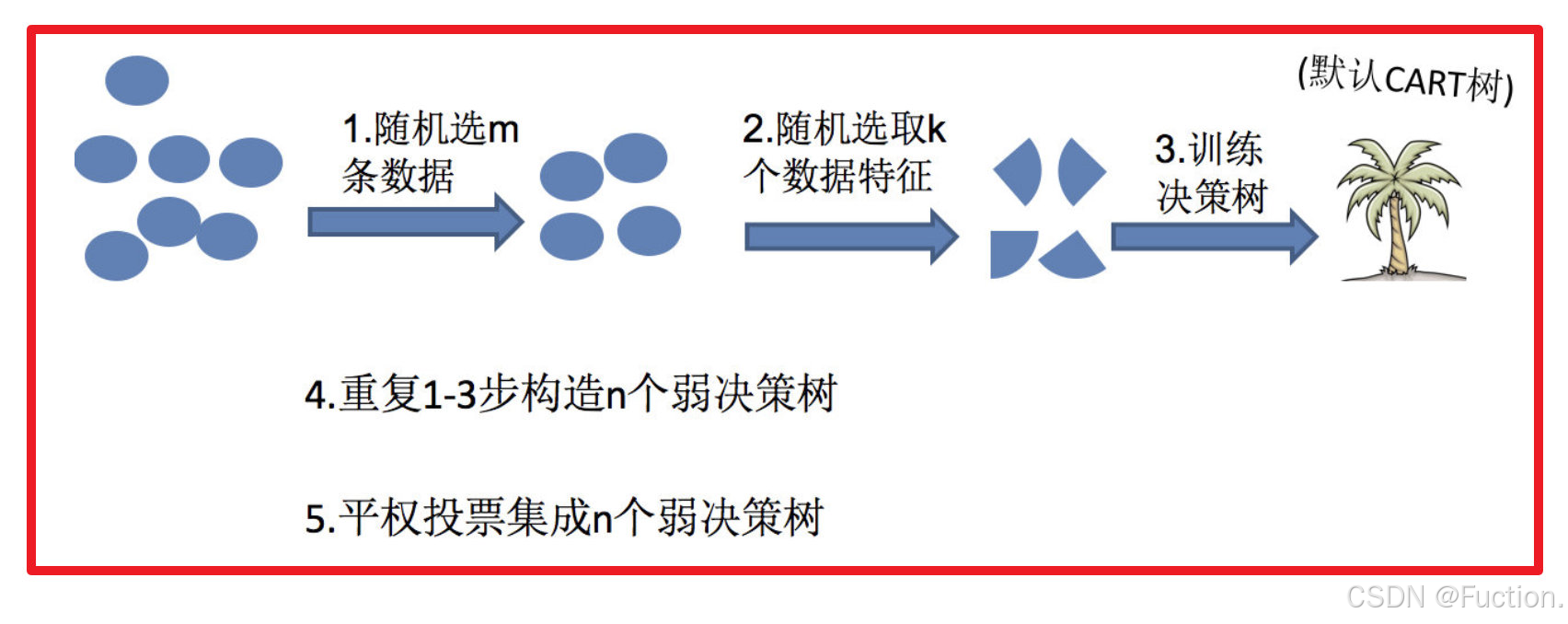
随机森林够造过程中的关键步骤(M表示特征数目)：

​  1)一次随机选出一个样本，有放回的抽样，重复N次(有可能出现重复的样本)

​  2) 随机去选出m个特征, m <

• 思考
  • 1.为什么要随机抽样训练集？　　
    • 如果不进行随机抽样，每棵树的训练集都一样，那么最终训练出的树分类结果也是完全一样的
  • 2.为什么要有放回地抽样？
    • 如果不是有放回的抽样，那么每棵树的训练样本都是不同的，都是没有交集的，这样每棵树都是“有偏的”，也就是说每棵树训练出来都是有很大的差异的；而随机森林最后分类取决于多棵树(弱分类器)的投票表决。
  • 综上：弱学习器的训练样本既有交集也有差异数据，更容易发挥投票表决效果

在随机森林构造过程中，如果进行有放回的抽样，我们会发现，总是有一部分样本我们选不到。

• 这部分数据，占整体数据的比重有多大呢？
• 这部分数据有什么用呢？

随机森林的 Bagging 过程，对于每一颗训练出的决策树 gt ，与数据集 D 有如下关系：

	g1g​1​​	g2g​2​​	g3g​3​​	……	gTg​T​​
(x1,y1)(x​1​​,y​1​​)	D1D​1​​	*	D3D​3​​		DTD​T​​
(x2,y2)(x​2​​,y​2​​)	*	*	D3D​3​​		DTD​T​​
(x3,y3)(x​3​​,y​3​​)	*	D2D​2​​	*		DTD​T​​
……
(xN,yN)(x​N​​,y​N​​)	D1D​1​​	D2D​2​​	*		*

对于星号的部分，即是没有选择到的数据，称之为 Out-of-bag(OOB)数据，当数据足够多，对于任意一组数据 (xn, yn) 是包外数据的概率为：

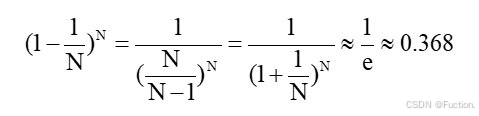
由于基分类器是构建在训练样本的自助抽样集上的，只有约 63.2％ 原样本集出现在中，而剩余的 36.8％ 的数据作为包外数据，可以用于基分类器的验证集。

经验证，包外估计（ Out-of-Bag Estimate）是对集成分类器泛化误差的 无偏估计.

在随机森林算法中数据集属性的重要性、分类器集强度和分类器间相关性计算都依赖于袋外数据。

• 当基学习器是决策树时，可使用包外样本来辅助剪枝 ，或用于估计决策树中各结点的后验概率以辅助对零训练样本结点的处理；
• 当基学习器是神经网络时，可使用包外样本来辅助早期停止以减小过拟合 。

• sklearn.ensemble.RandomForestClassifier(

n_estimators=10, # 森林里的树木数量默认10

criterion=’gini’, # 可选(default =“gini”) 基尼值

max_depth=None, # 树的最大深度 5,8,15,25,30

bootstrap=True, # 是否在构建树时使用放回抽样

max_features="auto”, # 每个决策树的最大特征数量

random_state=None,

min_samples_split=2) # 内部节点再划分所需最小样本数

实例化随机森林

# 随机森林去进行预测
from sklearn.ensemble import RandomForestClassifier
rf = RandomForestClassifier()

定义超参数的选择列表

param = {"n_estimators": [120,200,300,500,800,1200], "max_depth": [5, 8, 15, 25, 30]}

使用GridSearchCV进行网格搜索

# 超参数调优
from sklearn.model_selection import GridSearchCV
gc = GridSearchCV(rf, param_grid=param, cv=2)

gc.fit(x_train, y_train)

print("随机森林预测的准确率为：", gc.score(x_test, y_test))

注意：随机森林的建立过程树的深度、树的个数等需要进行超参数调优

​  Bagging + 决策树/线性回归/逻辑回归/深度学习… = bagging集成学习方法

经过上面方式组成的集成学习方法:

1. 均可在原有算法上提高约2%左右的泛化正确率
2. 简单, 方便, 通用

---

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import classification_report
import os 
os.chdir(r'集成学习data')


df = pd.read_csv("泰坦尼克号数据.csv")
df.info()

x = df[['Pclass','Age','Sex']]
y = df['Survived']
# x['Age'].fillna(x['Age'].mean(),inplace=True)
x.loc[:,['Age']] = x.loc[:,['Age']].fillna(x.loc[:,['Age']].mean())
x = pd.get_dummies(x)    # 进行热编码


x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.2, random_state=22)

dtc = DecisionTreeClassifier()
dtc.fit(x_train, y_train)
dtc_pred = dtc.predict(x_test)
dtc.score(x_test,y_test)

rfc = RandomForestClassifier(max_depth=6,random_state=9)
rfc.fit(x_train, y_train)
rfc_pred = rfc.predict(x_test)
rfc.score(x_test,y_test)

print("dtc_report:",classification_report(dtc_pred,y_test))
print("rfc_report:",classification_report(rfc_pred,y_test))

rf = RandomForestClassifier()
param={"n_estimators":[80,100,200], "max_depth": [2,4,6,8,10,12],"random_state":[9]}
gc = GridSearchCV(rf,param_grid=param,cv=2)
gc.fit(x_train,y_train)
print("随机森林预测的准确率为：", gc.score(x_test, y_test))

---

• bagging集成过程【知道】
  • 1.采样 — 从所有样本里面，采样一部分
  • 2.学习 — 训练弱学习器
  • 3.集成 — 使用平权投票
• 随机森林介绍【知道】
  • 随机森林定义
    • 随机森林 = Bagging + 决策树
  • 流程：
    • 1.随机选取m条数据
    • 2.随机选取k个特征
    • 3.训练决策树
    • 4.重复1-3
    • 5.对上面的若决策树进行平权投票
  • 注意：
    • 1.随机选取样本，且是有放回的抽取
    • 2.选取特征的时候吗，选择m<
    • M是所有的特征数
  • 包外估计
    • 如果进行有放回的对数据集抽样，会发现，总是有一部分样本选不到；
  • api
    • sklearn.ensemble.RandomForestClassifier()
• Bagging + 决策树/线性回归/逻辑回归/深度学习… = bagging集成学习方法【了解】
• bagging的优点【了解】
  • 1.均可在原有算法上提高约2%左右的泛化正确率
  • 2.简单, 方便, 通用