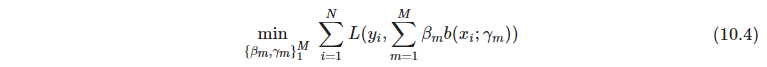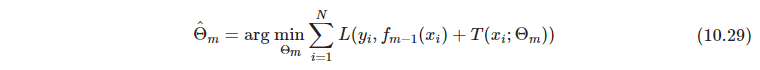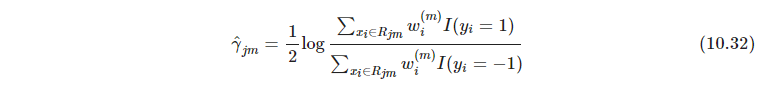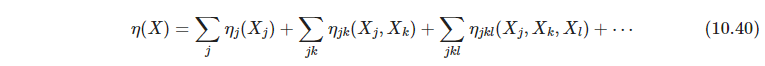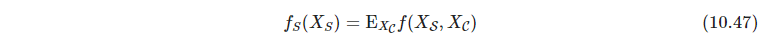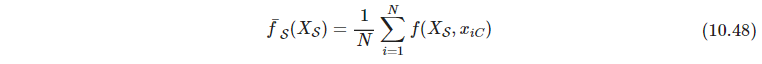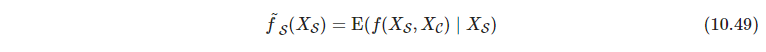目录
10.1 提升(Boosting)方法
- P337 Boosting和Bagging的联系是表面上的,boosting在根本上存在不同
- P339 AdaBoost.M1,也称为Discrete AdaBoost,如果基分类器返回实值预测,如映射到[-1, 1]的的概率,可修改得到Real AdaBoost,见Firedman et al. (2000)
- P340 单树桩和400Boosting的结果对比,和244结点树的对比
10.2 Boosting拟合加性模型
- P341 Boosting是用基本的“基函数”拟合加性展开additive expansions,这里基函数 G m ( x ) ∈ { − 1 , 1 } G_m(x)\in \{-1, 1\} Gm(x)∈{−1,1}
- P341 加性展开是本书许多方法的核心:单层神经网络;小波;MARS;树。这类函数优化如下loss
对许多损失函数和基函数,需要计算密集型的数值优化技术,但如果能快速求解单一基函数的子问题时,经常能找到代替方案
10.3 前向分段加性模型
- P342 前向分段加性模型forward stagewise additive modeling(注意该模型和P298 backfitting算法的区别,backfitting时一个个特征扫过去,该方法是一个个基模型)
10.4 指数损失和AdaBoost
- P344 AdaBoost通过forward-stagewise additive modeling的方式优化指数损失(有一个细节,PRML和ESL对于指数损失函数的推导差个系数2,不过最终结果一致)
10.5 为什么是指数损失
- P345 AdaBoost.M1算法最初是不是从这个角度得到的,它与基于指数损失的向前逐步加性建模的等价性在提出五年后被发现.通过研究指数损失函数准则的性质,可以深入了解这个过程并且找出可能改善的方式.
- P345 优化指数损失的期望得到log-odd/2,(另见PRML第14章P661)**所以AdaBoost可以看作是估计 P ( Y = 1 ∣ x ) P(Y=1|x) P(Y=1∣x)的log-odds的一半,进而用它的符号进行分类是合理的. 另一方面,考虑逻辑回归 P ( Y = 1 ∣ x ) = 1 1 + e − 2 f ( x ) P(Y=1|x)=\frac{1}{1+e^{-2f(x)}} P(Y=1∣x)=1+e−2f(x)1的形式直接建模,其二项分布负对数似然——也即交叉熵的期望极值也能算出是log-odd/2,其实就是在逻辑回归概率为真实值的时取到。所以对数似然和指数损失的极值相等。但要注意指数损失不是任何二值变量的概率密度函数对数似然。(深入思考,其实最大似然就是在优化交叉熵,给定概率p,要用q估计它,采用对数最大似然,就是优化 E p ( ln q ) \mathbb E_p(\ln q) Ep(lnq),变分法,得到最优时 q = p q=p q=p,所以最大似然估计的极值解是合理的,这应该也说明最大似然是渐近无偏的)
10.6 损失函数和鲁棒性
- P347 边缘margin y f ( x ) yf(x) yf(x),分类算法的损失函数应该对负边缘惩罚比正边缘大
- P347-348 指数损失对更负的边缘惩罚更大,从而更关注分的很错的点. 交叉熵损失则接近线性,在所有数据点上更均匀,在有噪声的情况,即贝叶斯误差率不接近0时,更鲁棒,尤其是训练数据有错标签时。这些情况下AdaBoost的表现显著退化
- P348 Huberized平方合页损失Huberized square hinge loss结合了交叉熵、平方损失和hinge loss的优良性质,图见P426. y f > 1 yf>1 yf>1时为0, y f < − 1 yf<-1 yf<−1时为线性,中间为均方误差(这看起来有点像回归中Smooth L1)。因为二项函数比指数更容易计算,经验表明这是交叉熵的有用替代
- P349 回归中均方误差和绝对值误差作为损失函数,也有类似分类中指数函数和交叉熵的讨论,两者分别在条件分布的期望和中位数处取极值。在有限样本上拟合过程中,平方误差损失更强调具有大的绝对值残差,因此更不鲁棒,尤其是对于长尾误差分布和异常值。M回归采用Huber损失准则,看起来就是Smooth-L1,小区域平方,大区域线性,注意0阶和1阶导连续,它对适度厚尾数据更好
10.7 数据挖掘的现成(Off-the-Shelf)过程
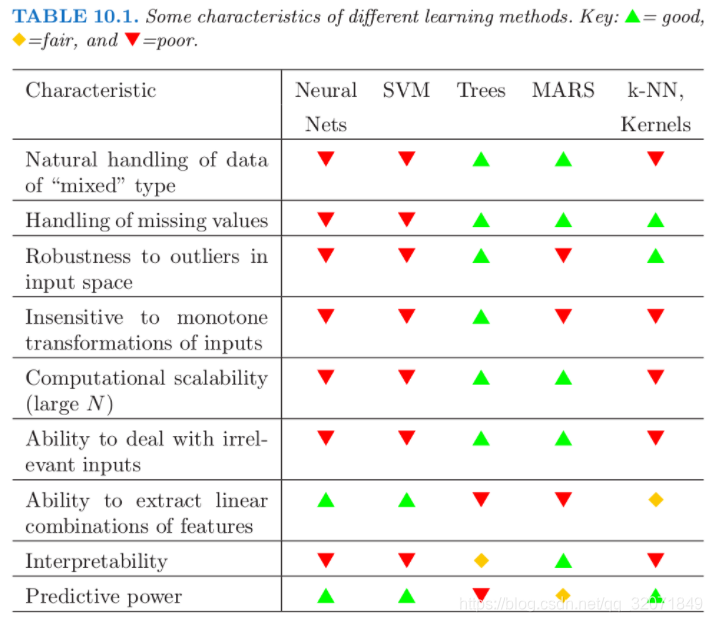
- P351 用表总结各个方法的特点
- P351 偏度意味着长尾。用log变换,能得到更好的拟合
- P352 "off-the-shelf"现成方法是指可以直接应用于数据,不用做太多预处理或学习过程的调整。数据挖掘对速度、可解释性、数据本身混乱的需求限制了off-the-shelf方法的使用。对数据挖掘来说,决策树是最能达到off-the-shelf过程的:1建树快;2解释性强,如果层不多的话;3易处理连续or类别特征和缺失值;4免疫单调变换;5抗离群点;6能抗无关特征
- P352 树的问题是预测不好,boosting决策树提高了准确率,但牺牲了一些树的优点:计算速度、可解释性、对AdaBoost而言的重叠类鲁棒性和噪声标注(应该是指数损失造成). gradient boosted model(GBM)是tree boosting的一般化,试图缓解这些问题,以便为数据挖掘提供准确而有效的off-the-shelf procedure(所以GBDT的出现动机是明确的,其受欢迎也是因为它的构建满足了这一动机,也即让树的预测更好一些)
10.8 垃圾邮件例子
- P353 McNemar检验,检验两模型的二分类能力是否相同。见习题10.6,西瓜书P40
- P353 偏相依图partial dependence plot,两变量偏相依图two-variable partial dependence plots
- P353 odds把概率从 [ 0 , 1 ] [0,1] [0,1]变为 R + \mathbb R^+ R+,log-odds进一步变为 R \mathbb R R
10.9 提升树Boosting Trees
- P356 提升树Boosting Trees是一堆树加起来,第
m
m
m步为
- P357 AdaBoost可看作是在树被限制为缩放分类树scaled classification tree时,Boosting Trees优化指数损失的特例。缩放分类树是指
β
T
\beta T
βT,其中
T
T
T对不同区域进行1和-1的二分类。如果不限制缩放分类树,则第
m
m
m棵树的叶子区域的最优拟合值为
从而导出另一种优化指数损失的算法(这看起来还不是梯度提升的思路,因为每个样本的目标值不知道) - P357 用Huber loss代替均方误差,或者交叉熵代替指数损失,得到更鲁棒的提升树boosting trees,不过这些鲁棒准则不会得到简单快速的boosting算法.
- P357 对于一般的损失函数。叶子区域找拟合值容易;但是如何划分区域生成一棵树,则很难,要看损失函数,不存在一般的准则,类似式(10.27)的近似就很重要了
10.10 梯度提升的数值优化
10.10.1 最速下降
- P358 写了一页Gradient boosting。这里的优化是最速下降steepest descent,梯度方向,线搜索优化走多远(回忆最优化课上学的,这里是完整的无约束最优化方法Methods with direction determination and line optimization)
10.10.2 梯度提升
- P359 式10.30找叶子节点拟合值和已知方向的线搜索有类似的感觉,区别就在于前者只针对单独的叶子区域
- P359 梯度提升中,损失函数变成了对梯度的均方误差。虽然这种方法和式10.29的提升树并不一致,但已经足够近似(拟合区域)
- P360 常用损失函数的梯度,注意分类中的交叉熵形式
10.10.3 梯度提升的实现
- P361 算法10.3中,梯度作为近似的loss只用来算树的划分区域,对于每个叶子节点,还是要用原先的Loss算拟合值(这里没有直接用梯度值的均值,我又看了一下统计学习方法,也是这么写的,woc以前我理解的gbdt是错的!也就是说梯度给出了树划分。GBDT很像线搜索,GBDT中的叶子表示这一堆点梯度差不多,可以看作是优化了约束方向,类似线搜索方向。而单纯的泛函中的梯度下降无法用于未见过的点。决策树中对特种空间中的附近位置没有训练样本的地方也起作用。这是GBDT的真正原理。) (所以提升树其实是一个更广泛的含义,比我之前理解的要广,GBDT只是借用了一下梯度)(xgboost则把原有loss function真的用二阶泰勒展开代替,树的划分和拟合都依据为带有正则的二阶近似loss。所以看来xgboost和书上这种只用一阶loss求划分区域的方式还是有一些不同的)
10.11 提升中树的合适大小
- P362 把树的叶子节点数固定,作为超参数。以防止前期树过大,降低模型效果增加计算量
- P362 一种考虑
J
J
J取值的方式是用方差分析ANOVA(analysis of variance)展开,
把拟合函数分成主影响main effect、二阶交叉项second-order interactions等等。对许多实际问题,低阶交叉影响占主要地位.如果模型有太高阶交叉项,比如过大的决策树,则可能性能不好。树的大小 J J J近似交叉项的阶数,不存在大于 J − 1 J-1 J−1阶的交叉项。 J = 2 J=2 J=2的树桩仅得到单变量的影响, J = 3 J=3 J=3允许有两变量交叉项影响 - P363 许多应用问题中, J = 2 J=2 J=2不够,但也不可能要求 J > 10 J>10 J>10,经验值是 4 ⩽ J ⩽ 8 4\leqslant J\leqslant 8 4⩽J⩽8
10.12 正则化
- P364 用CV找迭代轮次 M M M,该参数类似早停
10.12.1 收缩
- P365 类似学习率 ν \nu ν. 经验表明,比0.1小的 ν \nu ν测试误差更小,需要大 M M M,用早停确定
- P365 16.2.1节给出了前向分段收缩和L1正则的联系
10.12.2 子采样subsampling
- P365 随机梯度提升stochastic gradient boosting(这名字和sgd就差一个单词)。每次建树用子集,典型比例 η \eta η为 1 / 2 1/2 1/2,对于大数据集,可以更小些
- P365 这种操作有效的原因和Bagging可能类似,放到15章讨论
- P367 一般,通过前期尝试确定 J , ν , η J,\nu,\eta J,ν,η,将 M M M留下作为主要超参(感觉这意思类似训网络时看线)
10.13 解释性
10.13.1 特征的相对重要性Relative Importance
- P368 给出了决策树中特征重要性的一种度量方式,进一步该方式可扩展到加性树当中。是用平方损失的增益度量的。平方相关重要度squared relative importance,这种度量结果是平方相关的squared relevance,实际相关性还要开平方。由于这些度量相对,所以可以缩放,让最大的为100
- P368 该方法有一个多分类版本
10.13.2 偏相依图partial dependence plot
- P369 对于输入特征,一维二维都好画,维度再高就画以某个输入为条件的一堆图,称为网格图a trellis of plots
- P369 偏相依函数partial dependence functions的计算方法为:偏相依算模型中某特征子集对label的影响,可以以这一组特征子集的值为输入,其他所有补集特征求期望得到,求期望用训练集代替。这种方式计算量很大,因为特征子集的每一组取值都要扫一遍训练集中补集特征的值
但决策树模型可以加速计算,不用引用数据集,见习题10.11(没做。。)
- P370, 偏相依的解释需要注意:是在考虑完其他补集特征在
f
f
f上的平均影响之后,所选子集特征再在
f
f
f上的影响,不是忽略掉补集特征,直接对
f
f
f的影响,后者由条件期望给出
该式是仅用 X S X_S XS对 f f f的最优最小二乘近似。只有 X S X_S XS和 X C X_C XC独立时,两者才相等(后者这式子意思是,给定子集 X S X_S XS,然后求 p ( X C ∣ X S ) p(X_C|X_S) p(XC∣XS)分布下的期望,这有点像是贝叶斯派。 f f f关于 X S X_S XS的不确定性有 p ( X C ∣ X S ) p(X_C|X_S) p(XC∣XS)的成分,所以求个期望,这也即最小二乘近似的最优解。或者换一种说法,前者偏相依函数是 ∫ p ( X C ) f ( X S , X C ) d X C \int p(X_C)f(X_S,X_C)dX_C ∫p(XC)f(XS,XC)dXC,后者是 ∫ p ( X C ∣ X S ) f ( X S , X C ) d X C \int p(X_C|X_S)f(X_S,X_C)dX_C ∫p(XC∣XS)f(XS,XC)dXC,两者的分布差一个条件,如果 X S X_S XS与 X C X_C XC独立,两者自然相等了) - P370 子集很多,但通常只有强相关性的小子集有信息量(这里强相关性应该指的是相对重要的特征)
- P370 对于多分类,也可以看特征如何影响每一类 f k f_k fk,进一步如何影响对应类别概率的log-odds
10.14 例子
10.14.1 加州住房
- P371 测试误差看起来随着基模型数量M的单调降低,因此,M的具体值不重要,只要别太小.在许多应用中都趋向于是这种形式.收缩策略趋向于消除过拟合的问题,特别是对较大的数据集.
10.14.2 新西兰鱼
- P376 处理这个问题的方式很有趣。想知道某个地方有没有鱼,以及鱼的产量。用两个模型,第一个判断有没有,是一个分类问题;第二个在有的地方判断数量,是一个回归问题,这样训练集也被过滤的更干净。其中第二个模型把label进行log变换,因为假设物种数量服从了泊松分布(这里做log的理论依据我不太清楚,看起来是为了降偏度?)
10.14.3 人口数据的职业预测
文献笔记
- P384 关于AdaBoost的训练误差界,可以参考李航《统计学习方法》8.2节
参考文献:
[1] Trevor Hastie, Robert Tibshirani, Jerome Friedman. The Elements of Statistical Learning, Second Edition
[2] ESL CN