1 总体方差和样本方差
首先要分清总体和样本:
- 总体:研究对象的整个群体
比如总共10名玩家的年龄。 - 样本:总体的一个子集
比如其中5名队员玩家的年龄。
方差(Variance),衡量随机变量或一组数据离散程度的度量。根据总体和样本的区别分为总体方差和样本方差两种。
- 总体方差定义为:
σ 2 = ∑ i = 1 n ( X i − μ ) 2 n \sigma^{2}=\frac{\sum_{i=1}^{n}(X_{i}-\mu)^{2}}{n} σ2=n∑i=1n(Xi−μ)2
- 样本方差被定义为:
S 2 = ∑ i = 1 n ( X i − x ˉ ) 2 n − 1 S^{2}=\frac{\sum_{i=1}^{n}(X_{i}-\bar{x})^{2}}{n-1} S2=n−1∑i=1n(Xi−xˉ)2
在实际应用中是通过在总体中取样本,用其样本均值和样本方差 S 2 S^{2} S2来估计总体的均值 σ 2 \sigma^{2} σ2:
S 2 → σ 2 S^{2}\rightarrow\sigma^{2} S2→σ2
但是这样会产生一个问题,这两个在什么情况下能够等价?
下面举一个例子,假设我们抽取一个样本包含三个数据点: x 1 , x 2 , x 3 x_{1},x_{2},x_{3} x1,x2,x3,然后我们可以计算它的方差,当然这个方差还是除以 n n n意义下的方差:
S 2 = ( x 1 − μ ) 2 + ( x 2 − μ ) 2 + ( x 3 − μ ) 2 3 = 3 n μ 2 − 2 x 1 + x 2 + x 3 3 μ + x 1 2 + x 2 2 + x 3 2 3 \begin{aligned} S^{2} &=\frac{(x_{1}-\mu)^{2}+(x_{2}-\mu)^{2}+(x_{3}-\mu)^{2}}{3}\\ &=\frac{3}{n}\mu^{2}-2\frac{x_{1}+x_{2}+x_{3}}{3}\mu+\frac{x_{1}^{2}+x_{2}^{2}+x_{3}^{2}}{3} \end{aligned} S2=3(x1−μ)2+(x2−μ)2+(x3−μ)2=n3μ2−23x1+x2+x3μ+3x12+x22+x32
由上可见这是一个二次函数,我们可以将其画出来:
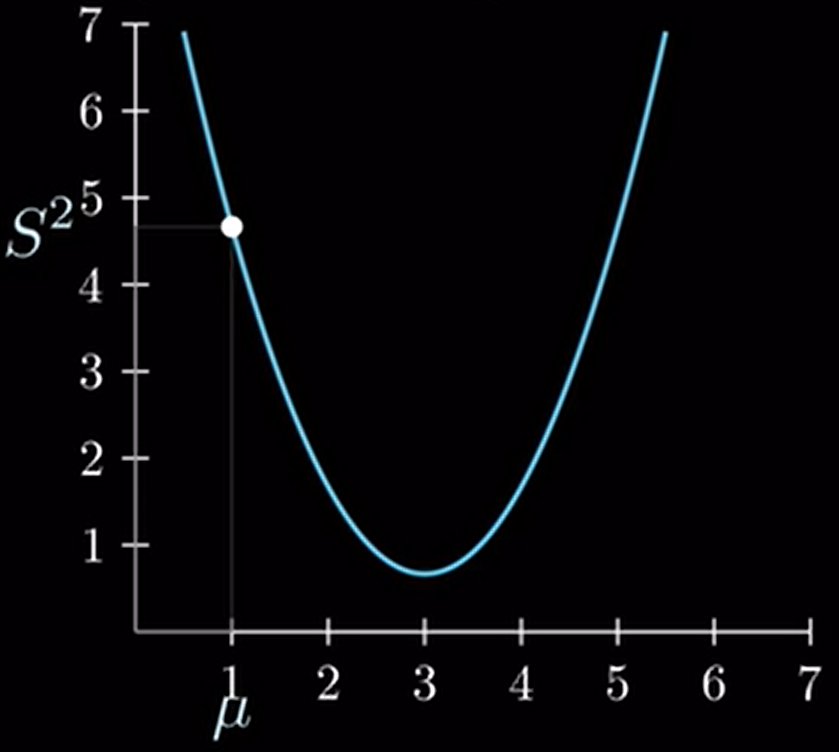
上图中,横坐标为均值 μ \mu μ,纵坐标为方差 S 2 S^{2} S2。当均值在变动的时候,方差也随之变化:

方差最小的地方对应的值为:
b − 2 a = − 2 x 1 + x 2 + x 3 3 − 2 3 3 = x ˉ \frac{b}{-2a}=\frac{-2\frac{x_{1}+x_{2}+x_{3}}{3}}{-2\frac{3}{3}}=\bar{x} −2ab=−233−23x1+x2+x3=xˉ
所以发现用样本均值算出的样本方差 S 2 S^{2} S2是其所有可能取值的下限。所以有关系:
∑ ( x − x ˉ ) 2 n < ∑ ( x − μ ) 2 N \frac{\sum(x-\bar{x})^{2}}{n}<\frac{\sum(x-\mu)^{2}}{N} n∑(x−xˉ)2<N∑(x−μ)2
其中 n n n为样本个数, N N N为总体个数,或者:
∑ i = 1 n ( X i − X ˉ ) 2 < ∑ i = 1 n ( X i − μ ) 2 \sum_{i=1}^{n}(X_{i}-\bar{X})^{2}<\sum_{i=1}^{n}(X_{i}-\mu)^{2} i=1∑n(Xi−Xˉ)2<i=1∑n(Xi−μ)2
这里需要分析一下是哪种情况??????
这会导致:
S 2 = ∑ i = 1 n ( X i − x ˉ ) 2 n < σ 2 = ∑ i = 1 n ( X i − μ ) 2 n S^{2}=\frac{\sum_{i=1}^{n}(X_{i}-\bar{x})^{2}}{n}<\sigma^{2}=\frac{\sum_{i=1}^{n}(X_{i}-\mu)^{2}}{n} S2=n∑i=1n(Xi−xˉ)2<σ2=n∑i=1n(Xi−μ)2
所以直观来说需要调节 S 2 S^{2} S2中的分母的大小(调小)。
2 方差的无偏估计
- 无偏估计
当我们用样本统计量来估计总体参数时,如果估计量的数学期望等于被估计参数的真实值,我们该估计量为被估计参数的无偏估计,即具有无偏性,是一种用于评价估计量优良性的准则。
而在这里我们就是希望:
E ( S 2 ) = σ 2 E(S^{2})=\sigma^{2} E(S2)=σ2
假设总体有10个数据,然后我们抽取5个数据来计算方差 S 1 2 S_{1}^{2} S12,然后重复这个步骤,最终得到 S 1 2 , S 2 2 , ⋯ , S 252 2 S_{1}^{2},S_{2}^{2},\cdots,S_{252}^{2} S12,S22,⋯,S2522,然后我们希望:
E ( S i 2 ) = S 1 2 + S 2 2 + ⋯ + S 252 2 252 = σ 2 E(S_{i}^{2})=\frac{S_{1}^{2}+S_{2}^{2}+\cdots+S_{252}^{2}}{252}=\sigma^{2} E(Si2)=252S12+S22+⋯+S2522=σ2
即用样本的方差去估计真实的总体方差
- 公式推导
E ( S 2 ) = E ( ∑ i = 1 n ( X i − x ˉ ) 2 n − 1 ) = 1 n − 1 E ( ∑ i = 1 n ( X i − x ˉ ) 2 ) = 1 n − 1 E ( ∑ i = 1 n ( ( X i − μ ) + ( μ − x ˉ ) ) 2 ) = 1 n − 1 E ( ∑ i = 1 n ( ( X i − μ ) 2 + 2 ( X i − μ ) ( μ − x ˉ ) + ( μ − x ˉ ) 2 ) ) \begin{aligned} E(S^{2}) &=E\left(\frac{\sum_{i=1}^{n}(X_{i}-\bar{x})^{2}}{n-1}\right)\\ &=\frac{1}{n-1}E\left(\sum_{i=1}^{n}(X_{i}-\bar{x})^{2}\right)\\ &=\frac{1}{n-1}E\left(\sum_{i=1}^{n}((X_{i}-\mu)+(\mu-\bar{x}))^{2}\right)\\ &=\frac{1}{n-1}E\left(\sum_{i=1}^{n}\left((X_{i}-\mu)^{2}+2(X_{i}-\mu)(\mu-\bar{x})+(\mu-\bar{x})^{2}\right)\right)\\ \end{aligned} E(S2)=E(n−1∑i=1n(Xi−xˉ)2)=n−11E(i=1∑n(Xi−xˉ)2)=n−11E(i=1∑n((Xi−μ)+(μ−xˉ))2)=n−11E(i=1∑n((Xi−μ)2+2(Xi−μ)(μ−xˉ)+(μ−xˉ)2))
1)其中上式的第一项可以化简为:
σ 2 = ∑ i = 1 n ( X i − μ ) 2 n → n σ 2 = ∑ i = 1 n ( X i − μ ) 2 \sigma^{2}=\frac{\sum_{i=1}^{n}(X_{i}-\mu)^{2}}{n}\rightarrow n\sigma^{2}=\sum_{i=1}^{n}(X_{i}-\mu)^{2} σ2=n∑i=1n(Xi−μ)2→nσ2=i=1∑n(Xi−μ)2
由于 n σ 2 n\sigma^{2} nσ2为常数,则:
1 n − 1 E ( ∑ i = 1 n ( X i − μ ) 2 ) = 1 n − 1 E ( n σ 2 ) = n n − 1 σ 2 \frac{1}{n-1}E\left(\sum_{i=1}^{n}(X_{i}-\mu)^{2}\right)=\frac{1}{n-1}E(n\sigma^{2})=\frac{n}{n-1}\sigma^{2} n−11E(i=1∑n(Xi−μ)2)=n−11E(nσ2)=n−1nσ2
2)前式第二项可以化简为:
1 n − 1 E ( ∑ i = 1 n 2 ( X i − μ ) ( μ − x ˉ ) ) = 2 n − 1 E ( ( μ − x ˉ ) ( ∑ i = 1 n ( X i − μ ) ) ) = 2 n − 1 E ( ( μ − x ˉ ) ( ∑ i = 1 n X i − n μ ) ) = 2 n − 1 E ( ( μ − x ˉ ) ( n x ˉ − n μ ) ) = − 2 n n − 1 E ( ( μ − x ˉ ) 2 ) \begin{aligned} &\ \ \ \ \ \frac{1}{n-1}E\left(\sum_{i=1}^{n}2(X_{i}-\mu)(\mu-\bar{x})\right)\\ &=\frac{2}{n-1}E\left((\mu-\bar{x})\left(\sum_{i=1}^{n}(X_{i}-\mu)\right)\right)\\ &=\frac{2}{n-1}E\left((\mu-\bar{x})\left(\sum_{i=1}^{n}X_{i}-n\mu\right)\right)\\ &=\frac{2}{n-1}E\left((\mu-\bar{x})\left(n\bar{x}-n\mu\right)\right)\\ &=-\frac{2n}{n-1}E\left((\mu-\bar{x})^{2}\right)\\ \end{aligned} n−11E(i=1∑n2(Xi−μ)(μ−xˉ))=n−12E((μ−xˉ)(i=1∑n(Xi−μ)))=n−12E((μ−xˉ)(i=1∑nXi−nμ))=n−12E((μ−xˉ)(nxˉ−nμ))=−n−12nE((μ−xˉ)2)
3)第三项可以化简为:
1 n − 1 E ( ∑ i = 1 n ( μ − x ˉ ) 2 ) = n n − 1 E ( ( μ − x ˉ ) 2 ) \begin{aligned} &\ \ \ \ \ \frac{1}{n-1}E\left(\sum_{i=1}^{n}(\mu-\bar{x})^{2}\right)\\ &=\frac{n}{n-1}E\left((\mu-\bar{x})^{2}\right)\\ \end{aligned} n−11E(i=1∑n(μ−xˉ)2)=n−1nE((μ−xˉ)2)
4)合并第二项和第三项得:
− n n − 1 E ( ( μ − x ˉ ) 2 ) -\frac{n}{n-1}E\left((\mu-\bar{x})^{2}\right)\\ −n−1nE((μ−xˉ)2)
而
E ( ( μ − x ˉ ) 2 ) = E ( ( 1 n ∑ i = 1 n x i − 1 n n μ ) 2 ) = 1 n 2 E ( ( ∑ i = 1 n x i − n μ ) 2 ) = 1 n 2 E ( ( ∑ i = 1 n x i − E ( ∑ i = 1 n x i ) ) 2 ) \begin{aligned} &\ \ \ \ \ E\left((\mu-\bar{x})^{2}\right)\\ &=E\left(\left(\frac{1}{n}\sum_{i=1}^{n}x_{i}-\frac{1}{n}n\mu\right)^{2}\right)\\ &=\frac{1}{n^{2}}E\left(\left(\sum_{i=1}^{n}x_{i}-n\mu\right)^{2}\right)\\ &=\frac{1}{n^{2}}E\left(\left(\sum_{i=1}^{n}x_{i}-E\left(\sum_{i=1}^{n}x_{i}\right)\right)^{2}\right)\\ \end{aligned} E((μ−xˉ)2)=E⎝ ⎛(n1i=1∑nxi−n1nμ)2⎠ ⎞=n21E⎝ ⎛(i=1∑nxi−nμ)2⎠ ⎞=n21E⎝ ⎛(i=1∑nxi−E(i=1∑nxi))2⎠ ⎞
此时将 ∑ i = 1 n x i \sum_{i=1}^{n}x_{i} ∑i=1nxi看作变量,则:
E ( ( ∑ i = 1 n x i − E ( ∑ i = 1 n x i ) ) 2 ) = v a r ( ∑ i = 1 n x i ) E\left(\left(\sum_{i=1}^{n}x_{i}-E\left(\sum_{i=1}^{n}x_{i}\right)\right)^{2}\right)=var\left(\sum_{i=1}^{n}x_{i}\right) E⎝ ⎛(i=1∑nxi−E(i=1∑nxi))2⎠ ⎞=var(i=1∑nxi)
当 x i x_{i} xi之间是相互独立的时候:
v a r ( ∑ i = 1 n x i ) = ∑ i = 1 n v a r ( x i ) var\left(\sum_{i=1}^{n}x_{i}\right)=\sum_{i=1}^{n}var\left(x_{i}\right) var(i=1∑nxi)=i=1∑nvar(xi)
所以:
E ( ( ∑ i = 1 n x i − E ( ∑ i = 1 n x i ) ) 2 ) = ∑ i = 1 n v a r ( x i ) = ∑ i = 1 n σ 2 E\left(\left(\sum_{i=1}^{n}x_{i}-E\left(\sum_{i=1}^{n}x_{i}\right)\right)^{2}\right)=\sum_{i=1}^{n}var\left(x_{i}\right)=\sum_{i=1}^{n}\sigma^{2} E⎝ ⎛(i=1∑nxi−E(i=1∑nxi))2⎠ ⎞=i=1∑nvar(xi)=i=1∑nσ2
所以:
E ( ( μ − x ˉ ) 2 ) = 1 n 2 E ( ( ∑ i = 1 n x i − E ( ∑ i = 1 n x i ) ) 2 ) = 1 n 2 ∑ i = 1 n σ 2 = 1 n σ 2 \begin{aligned} &\ \ \ \ \ E\left((\mu-\bar{x})^{2}\right)\\ &=\frac{1}{n^{2}}E\left(\left(\sum_{i=1}^{n}x_{i}-E\left(\sum_{i=1}^{n}x_{i}\right)\right)^{2}\right)\\ &=\frac{1}{n^{2}}\sum_{i=1}^{n}\sigma^{2}\\ &=\frac{1}{n}\sigma^{2}\\ \end{aligned} E((μ−xˉ)2)=n21E⎝ ⎛(i=1∑nxi−E(i=1∑nxi))2⎠ ⎞=n21i=1∑nσ2=n1σ2
所以:
− 1 n − 1 E ( ( μ − x ˉ ) 2 ) = − n n − 1 1 n σ 2 = − 1 n − 1 σ 2 -\frac{1}{n-1}E\left((\mu-\bar{x})^{2}\right)=-\frac{n}{n-1}\frac{1}{n}\sigma^{2}=-\frac{1}{n-1}\sigma^{2} −n−11E((μ−xˉ)2)=−n−1nn1σ2=−n−11σ2
5)所以原式得:
E ( S 2 ) = n n − 1 σ 2 − 1 n − 1 σ 2 = σ 2 \begin{aligned} E(S^{2}) &=\frac{n}{n-1}\sigma^{2}-\frac{1}{n-1}\sigma^{2}\\ &=\sigma^{2} \end{aligned} E(S2)=n−1nσ2−n−11σ2=σ2
由此证毕。
3 从自由度角度理解样本方差为什么除以 n − 1 n-1 n−1?
现在从自由度的角度解释为何样本方差为什么除 n − 1 n-1 n−1。首先明确自由度的概念:自由度(degree of freedom,df)指的是计算某一统计量时,取值不受限制的变量个数,比如取三个变量 x , y , z x,y,z x,y,z,然后计算平均值为 x + y + z 3 \frac{x+y+z}{3} 3x+y+z,则此时自由度为3个。但是给定约束 x + y + z = 10 x+y+z=10 x+y+z=10之后,假设 x , y x,y x,y为自由变量,则此时 z z z不再是自由变量,平均值的自由度降为2个。
应用在样本方差的公式中:
S 2 = ∑ i = 1 n ( X i − x ˉ ) 2 n S^{2}=\frac{\sum_{i=1}^{n}(X_{i}-\bar{x})^{2}}{n} S2=n∑i=1n(Xi−xˉ)2
假设抽取三个数据,其中 x ˉ = x 1 + x 2 + x 3 3 \bar{x}=\frac{x_{1}+x_{2}+x_{3}}{3} xˉ=3x1+x2+x3,则计算方差的公式的分母 ( x 1 − x ˉ ) 2 + ( x 2 − x ˉ ) 2 + ( x 3 − x ˉ ) 2 (x_{1}-\bar{x})^{2}+(x_{2}-\bar{x})^{2}+(x_{3}-\bar{x})^{2} (x1−xˉ)2+(x2−xˉ)2+(x3−xˉ)2的自由度不再是3个,而应该是2个,应为当给定 x 1 , x 2 x_{1},x_{2} x1,x2或者其中两项时, ( x 3 − x ˉ ) 2 (x_{3}-\bar{x})^{2} (x3−xˉ)2已经确定了。
值得注意的是,这里样本方差分母上的自由度不再是变量的自由度,而是以 ( x i − x ˉ ) 2 (x_{i}-\bar{x})^{2} (xi−xˉ)2的自由度,否则的话,变量的自由度依旧为3不变!
所以当样本量为 n n n的时候,计算样本方差需要除以自由度 n − 1 n-1 n−1。
| 统计量 | 自由度 | 公式 |
|---|---|---|
| 样本平均数 | n n n | ∑ i = 1 n x i n \frac{\sum_{i=1}^{n}x_{i}}{n} n∑i=1nxi |
| 样本方差 | n − 1 n-1 n−1 | ∑ i = 1 n ( X i − x ˉ ) 2 n − 1 \frac{\sum_{i=1}^{n}(X_{i}-\bar{x})^{2}}{n-1} n−1∑i=1n(Xi−xˉ)2 |
| 一元回归 | n − 2 n-2 n−2 | σ ^ 2 = ∑ i = 1 n e i 2 n − 2 \hat{\sigma}^{2}=\frac{\sum_{i=1}^{n}e_{i}^{2}}{n-2} σ^2=n−2∑i=1nei2 |
| 多元回归 | n − k − 1 n-k-1 n−k−1 | σ ^ 2 = ∑ i = 1 n e i 2 n − k − 1 \hat{\sigma}^{2}=\frac{\sum_{i=1}^{n}e_{i}^{2}}{n-k-1} σ^2=n−k−1∑i=1nei2 |
参考资料: