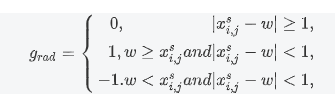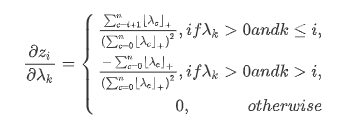基于换衣服的行人重识别

论文地址：Person Re-identification by Contour Sketch under Moderate Clothing Change

问题总结

现有行人重识别的缺点：过度依赖衣服颜色导致将衣着相似的人混淆。

本文基于人物图像的轮廓草图来执行跨服装的Re-ID，以利用人体的形状而不是颜色信息来提取对适度服装变化鲁棒的特征。

算法概述

假设短时间内行人轮廓变化不大并且天气也没有显著变化时，要从轮廓草图中提取可靠且有区别的曲线模式，轮廓草图为克服同一个人的图像之间的差异提供了可靠和有效地视觉线索。本文开发了一种基于学习的空间极坐标变换(SPT)来自动选择/采样相对不变的、可靠的和有区别的局部曲线模式。此外，我们引入角度特定提取器(ASE)来选择健壮和有区别的细粒度特征。最后，学习多数据流网络的特征集合，以提取多粒度(即，全局粗粒度和局部细粒度)特征，并在一个人穿着不同时重新识别他/她。采用交叉熵损失和三元组边缘损失作为多数据流网络的目标函数来挖掘更多的判别服装变化不变的特征，这增加了区分人的类间差距。

行人重识别算法概述

ReID发展从提取特征和距离度量学习到基于深度学习的方法。这些是为了克服视角、背景混乱、身体姿势、比例和遮挡的变化。最近通过采用深度特征以及使用度量学习的方法、语义属性和外观模型，ReID的性能得以显著提升。

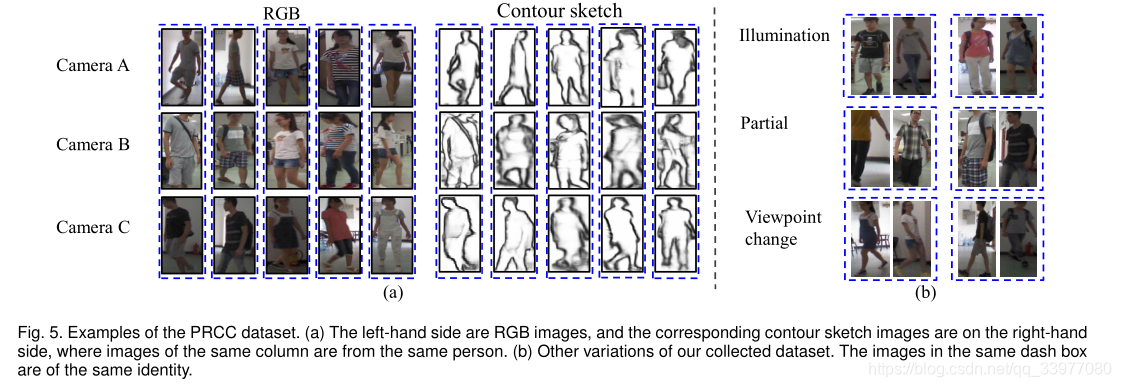
提出一个数据集（PRCC），针对换衣服的问题：该数据集包含221个人的33698副图像，由三个摄像机拍摄。A,B摄像机中，行人穿着相同的衣服，C摄像机中， 穿着不同的衣服。

将输入改变为由RGB图像生成的轮廓草图图像。从RGB图像估计人体的2D形状，提出SPT和多数据流模型来变换草图图像，已提取选择性的多粒度可靠特征。而且本文的重点是匹配用不同摄像机视角拍摄的人物轮廓草图图像。

总结

假设：穿相似厚度的衣服，天气无显著变化，人形状无显著变化。

模型思路：

• 从轮廓草图图像提取有区别的特征来解决适度服装变化。首先在神经网络中引入可学习的空间极坐标变换SPT来选择有区别的曲线模式，引入特定角度来挖掘细粒度的角度特征，然后通过改变SPT采样范围聚合多（粗细粒度）粒度特征，形成多数据流

• 可变形卷积通过改变卷积核的形状来聚焦曲线从而获得更好的性能

• SPT：选择有区别的曲线模式

• ASE：从特定角度挖掘健壮的细粒度的特征，即提取多粒度特征

• 直接对轮廓草图图像进行深度卷积并不能有效地提取跨服装人物身份识别的可靠性和判别性特征

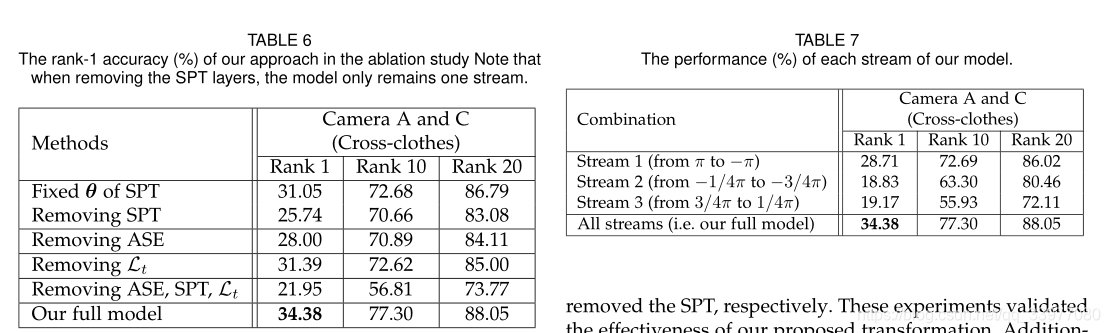
• stream2 和 stream3 从不同区域得到特征，所以它们的特征互补

结果和消融实验

数据集介绍

PRCC数据集中的图像不仅包括同一个人在不同相机视图中的服装变化，还包括其他变化，例如照明、遮挡、姿势和视点的变化。一般来说，每个相机视图中每个人有50幅图像；因此，数据集中包括每个人的大约152张图像，总共33698张图像。

在生成轮廓草图图像时，使用整体嵌套边缘检测模型，并采用输出作为轮廓草图。我们将数据集随机分为训练集和测试集。训练集由150人组成，测试集由71人组成，训练集和测试集在身份方面没有重叠。在训练期间，我们从训练集中选择了25%的图像作为验证集。

实验配置

测试集分为gallery set和probe set（图库集和探针集）。对于测试集中的每个身份，我们在相机视图A中随机选择一幅图像，形成图库集进行单次匹配。摄像机视图B和摄像机视图C中的所有图像都用于探头组。相机视图A和B之间的人物匹配是在不改变服装的情况下执行的，而相机视图A和C之间的匹配是跨服装匹配。根据累积的匹配特征，特别是前k的匹配精度来评估结果。我们用随机选择的图库集重复上述评估10次，并计算平均性能。

在PRCC的结果：

SketchNet：是为跨模态搜索而设计的。

可变形卷积可以通过改变卷积核的形状来聚焦曲线，从而获得更好的性能。

结果如下表所示：

讨论：

1.HOG，LBP，LOMO：表示纹理信息的手工特征

KISSME，XQDA：通过度量学习进行性能提升

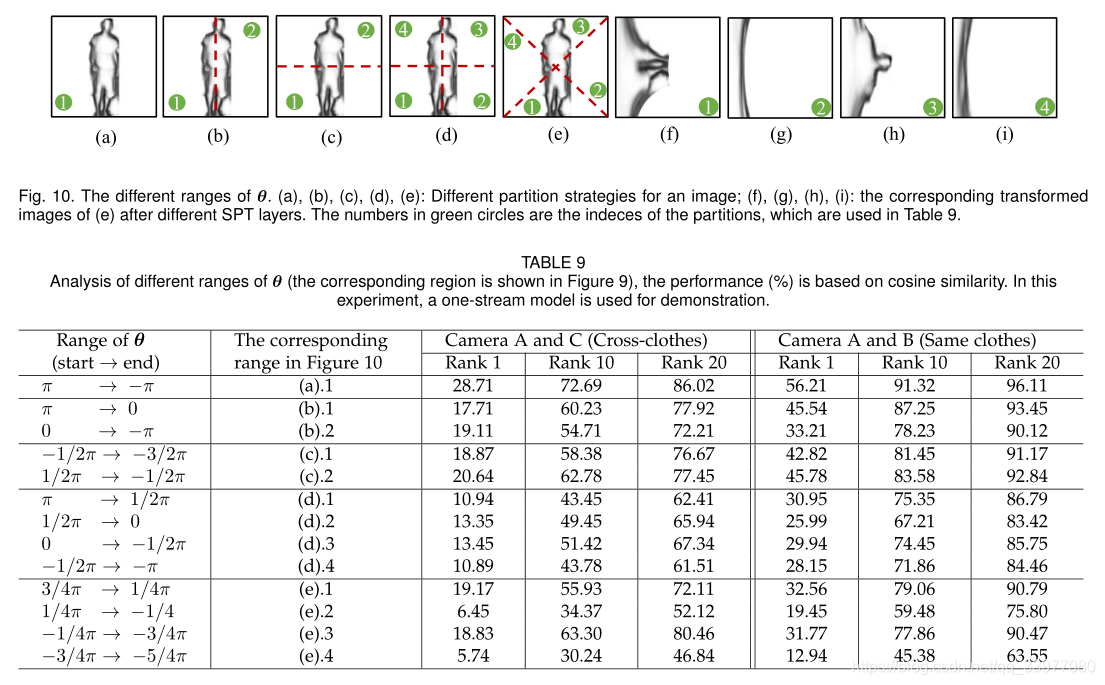
3.评估基于轮廓波形的特征对服装变化是否有效

基于形状匹配 他们缺乏对视图和服装变化的建模

4.基于深度学习的方法 对相同衣服时深度学习方法性能较好

6.是基于单图检索 SketchNet：轮廓草图与同一身份的RGB图像组成正对，轮廓草图与不同身份你的RGB图像组成负对。

7.使用脸部识别方法

8.可变形CNN 和 STN应用于仿射变换

将换衣服分为三类：上身衣服、下身衣服和其他情况、表2就说明这些情况：

结果：如果这个人完全换衣服，基于RGB的方法是无效的。请注意，基于RGB的方法在这种情况下不会完全失败，因为RGB图像也包含一些轮廓信息。或者一个人剧烈的改变衣服文章的方法就会失败。

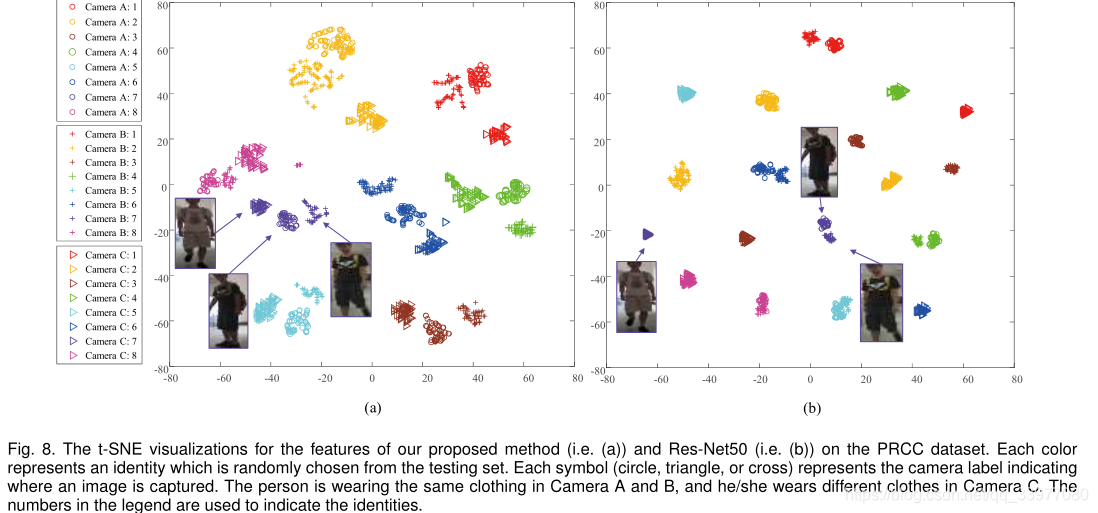
使用t-SNE用来可视化文章的方法（轮廓图像作为输入，彩色图像作为输入的最终学习特征）。

视点变化很大的情况：尽管我们提出的方法由于剧烈的视点变化而在一定程度上降低了性能，但它大大优于最好的基于RGB的方法。在服装变化的情况下，与基于颜色的视觉提示相比，轮廓相对稳定，因为服装变化是不可预测的并且难以建模，而轮廓变化相对更可预测。

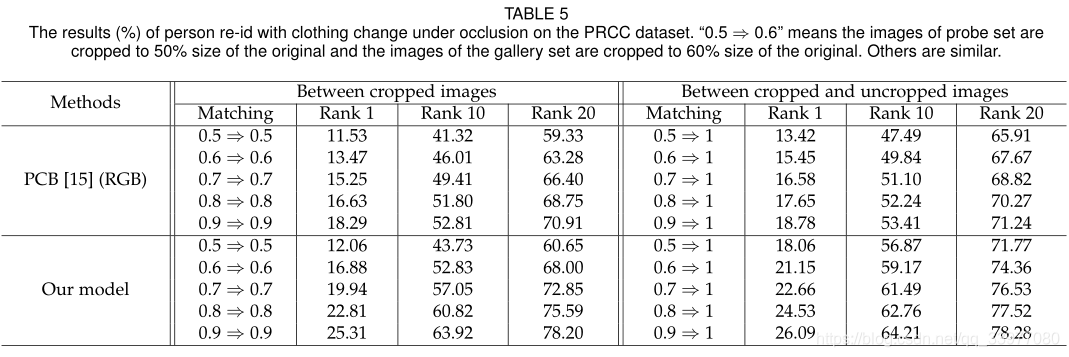
将原始图像裁剪成50%-100%的大小进行匹配。

解决遮挡问题的一个更有前途的方法是结合零件对齐和局部到局部或全局到局部的匹配。

消融实验

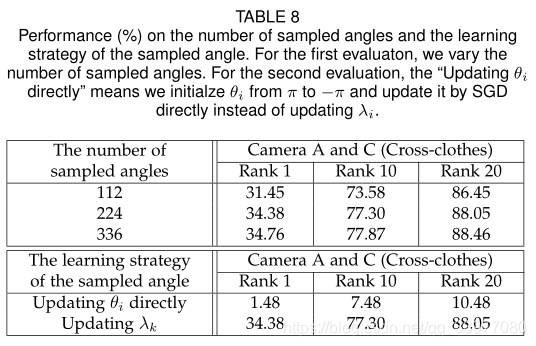
SPT，ASE，Triplet Loss各部分对模型性能的影响，以及七个流中每个流对模型性能的影响。直接对轮廓草图图像进行深度卷积并不能有效地提取跨服人身份识别的可靠特征和判别特征。当采样角度固定时，$\theta$范围大意味着变换后的图像将丢失更多细节。，因为流2和流3的图像是从轮廓草图图像的不同区域变换而来的，所以它们的特征是互补的。

采样角度对模型的影响：如果直接更新$\theta$采样角度的范围和顺序将被打乱。表中变量是取样角度的数量。

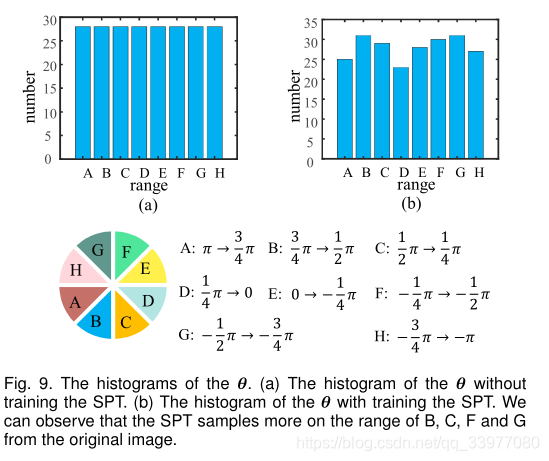
$\theta$范围的研究：形状的那一部分重要。将$\theta$直方图可视化，展示轮廓的哪一部分更具有辨识度。SPT从原始图像中在B、C、F和G范围内采样较多，在A和d范围内采样较少。这表明B、C、F和G范围内的轮廓更具区分性。可以通过改变θ的约束来提取不同的局部特征。

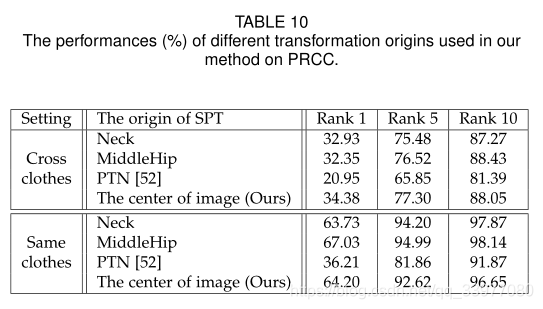
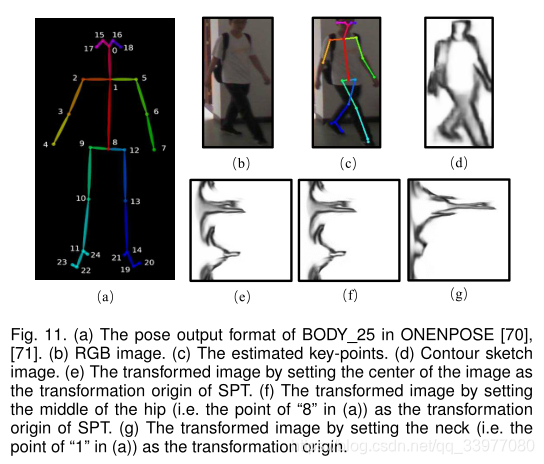
另外，SPT可能结合身体关键点信息。它最初使用轮廓草图的中心作为变换原点，轮廓草图中心接近于人体中心的假设。SPT也可以使用姿势关键点作为变换原点。大多数图像与其他关键点相比，颈部和臀部中间点的估计更准确。分别使用颈部和臀部中间的点作为SPT的变换原点：

第一行中的图像是填充后PRCC数据集中同一个人的轮廓草图图像。在我们的方法中，通过使用PTN，第二行中的图像是第一行的对应变换图像。在我们的方法中，通过使用所提出的SPT，第三行中的图像是第一行的对应变换图像。

算法详述

学习DNN中的空间极坐标变换

学习有分辨性的曲线，需要用到从一个轮廓到另一个轮廓的变换：$U\in {\mathbb{R}}^{H\times W}\to V\in {\mathbb{R}}^{N\times M}$.这个变换可以表示为：
$$V=\tau (U)$$
将轮廓草图转换为极坐标，以增强轮廓草图图像的旋转和比例不变性。通过这样的方式，期望基于极角选择鉴别曲线模式。

Transformation by differentiable polar transformation

直角坐标和极坐标的表示如下：
$$r=\sqrt{x^2+y^2},\phi =\arctan \frac{y}{x}$$

可微极坐标变换包括两个步骤：计算采样网络和执行采样。采样网格是由一对采样角度和采样半径组成。${\theta }_i$是草图图像的第i个采样角。即极坐标中像素的角度，从$\pi to-\pi$，其中$i\in [0,N]$.这里$r_j=j\times R/M$表示极坐标中的采样半径，R是最大的采样半径，$j\in [0,M]$。基于采样角度和采样半径，我们通过以下方式生成采样网格：
$$x_{i,j}^s=r_j\cos {\theta }_i,y_{i,j}^s=r_j\sin {\theta }_i$$
等式左边代表原始轮廓草图图像的坐标，i，j代表变换图像的第i行和第j列。

生成采样网格后，下一步是对轮廓草图图像进行插值采样。设$v_{i,j}$为变换后图像的像素值；我们可以使用可微分双线性采样核来生成变换图像:
$$v_{i,j}=\sum _h^H\sum _w^W{u}_{h,w}\times \lfloor 1-|x_{i,j}^s-w|{\rfloor }_{+}\times \lfloor 1-|y_{i,j}^s-h|{\rfloor }_{+}$$
$\lfloor \cdot {\rfloor }_{+}$代表它和0的最大值。$u_{h,w}$代表轮廓草图$U\in R^{H\times W}$的像素值.

Learnable spatial polar transformation

这个可学习的空间极坐标变换SPT是只有一部分轮廓部分被自动选择/采样用于空间变换。使用神经网络来自动学习采样角度，而不是固定其值。通过这种方式将更多的注意力集中在有区别的曲线模式上。因此，在空间变换的轮廓草图上，曲线模式不太可能被均匀采样，并且只采样选择性的曲线模式。

对于不同的角度，模型可通过变换表示为：
$$V=\tau (U,\theta )$$
DNN中使用反向传播梯度来更新参数，使用SGD或其他来相对于目标函数优化参数。如果使用SGD直接更新θ，则采样角度会在不考虑采样角度范围的情况下更新，采样角度的顺序(即极坐标中的${\theta }_{i+1}\le {\theta }_i$)会被打乱，将${\theta }_i$参数化：
$${\theta }_i=f(z_i),z_i=\frac{{\sum }_{k=0}^i\lfloor {\lambda }_k{\rfloor }_{+}}{{\sum }_{k=0}^N\lfloor {\lambda }_k{\rfloor }_{+}}$$
${\lambda }_k$是SPT变换的参数，f是线性函数，将中间变量映射到角度的特定范围。
$$f(z_i)=(b-a)\times z_i+a（7）$$
采样角度由${\lambda }_i$计算。通过映射${\lambda }_k\to z_i$隐式的共同考虑采样角度之间的关系。首先将其初始化为一个常量，因此采样角度均匀分布，然后更新${\lambda }_k$,计算训练中的${\theta }_i$.

学习$\theta$

反向传播中。相对于$x_{i,j}^s$的梯度$v_{i,j}$表示为：
$$\frac{\partial v_{i,j}}{\partial x_{i,j}^s}=\sum _h^H\sum _w^W{u}_{h,w}\max (0,1-|y_{i,j}^s-h|)\times g_{rad}$$

KaTeX parse error: Unknown column alignment: 1 at position 35: …begin{array}{rc1̲} 0,~~~~~~~~~~~…

计算$x_i$相对于${\theta }_i$的梯度：$\frac{\partial x_{i,j}^s}{\partial {\theta }_i}=-r_j\sin {\theta }_i$.同样的方式得到：$\frac{\partial v_{i,j}}{\partial y_{i,j}^s},\frac{\partial y_{i,j}^s}{\partial {\theta }_i}$，又因为f是线性函数，很容易得到梯度：

KaTeX parse error: Unknown column alignment: 1 at position 69: …begin{array}{rc1̲} \frac {\sum^…
因此，可以更新${\lambda }_k$来更新${\theta }_i$.如果我们固定θ并初始化所有${\lambda }_k$，则从轮廓草图图像的不同区域对变换后的图像进行均等采样。相比之下，如果θ是可学习的，则变换后的图像将从包含更多身份信息的特定区域进行更多采样。

Insight undersighting

该变换可被视为相对于其中心展开轮廓草图图像，即展开轮廓草图图像的极坐标空间。变换图像的每一行都是从具有相同极角的原始图像的像素中采样的。事实上，通过使用SPT，当卷积层应用于变换图像时，卷积层的感受野反而是扇形或锥形的,而不是矩形形状。

SPT侧重于学习采样角度，这有助于学习多粒度特征，并将极坐标变换的原点设置在人体轮廓草图图像的中心；

PTN（文章提到的另一种方法）学习了每幅图像的极坐标变换的起源。因此，PTN可以学习不同的变换原点，从而获得不同输入图像的不同变换图像，即使它们来自相同的身份，这对于重新识别是无效的

特定角度提取

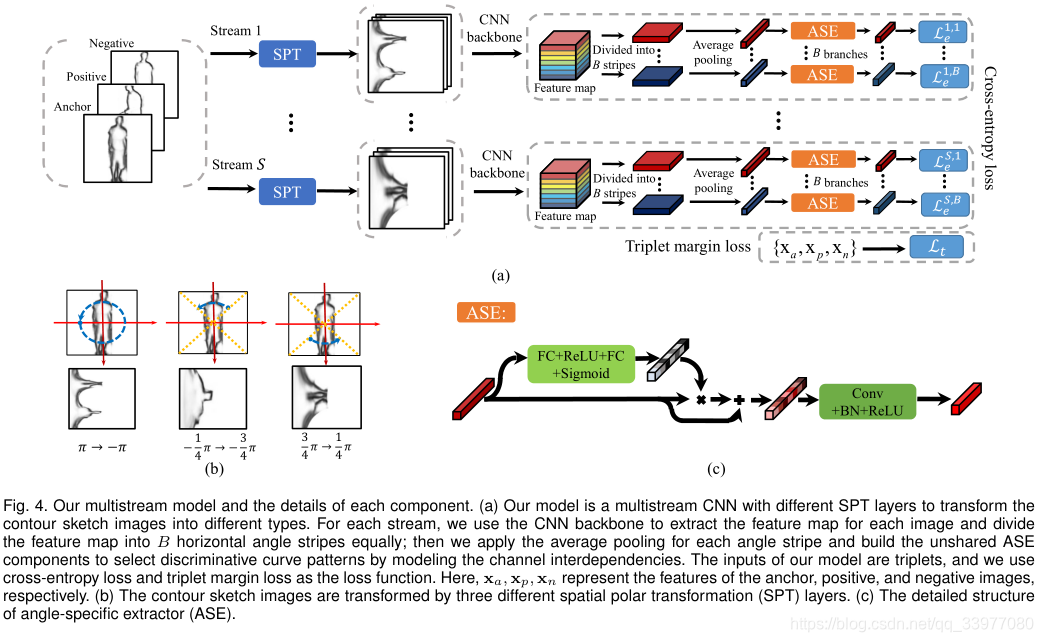
我们希望进一步开发细粒度的角度特定特性，以抵抗相机视图中的服装变化。根据变换图像中相应的角度范围，将特征图分割成B角度条带，然后对每个角度条带进行平均合并。然后，不同角度条纹的特征被馈送到不同的CNN分支，以学习精细的和特定角度的特征。

该模型是一个多数据流CNN，具有不同的SPT层，用于将轮廓草图图像转换为不同的类型。对于每个流，我们使用CNN主干为每个图像提取特征图，并将特征图平均分成B个水平角条纹；然后，我们对每个角度条带应用平均池，并通过对通道相互依赖性建模来构建非共享ASE分量，以选择有区别的曲线模式。模型的输入是三元组，我们使用交叉熵损失和三元组边际损失作为损失函数。三元组的三个元组是锚点、正样本和负样本。轮廓草图图像通过三个不同的空间极坐标变换层进行变换。

通过建模通道间的依赖关系来重新加权通道，因为不同的通道对识别的贡献不同。由于不同角度条带的通道间依赖性不同，我们使用非共享图层来建模不同角度条带的依赖性。以这种方式建模相互依赖关系有助于对相对不变的曲线模式给予更多关注。这些通道间的依赖关系充当通道权重，用于通过元素方式的产品重新加权特征图，以建模特征图的通道之间的相互依赖关系。

计算通道之间的相关性。选通机制包括权重为$W_j$全连接层，激活函数$\zeta$,群众为$Q_j$的全连接层以及激活函数$\sigma$，L代表输入通道的数量，r是缩减率。$a_j$是输入向量（平均池化后个角的特征），第j个分支的依赖性$d_j$:
$${\mathbf{d}}_j=\sigma ({\mathbf{Q}}_j\zeta ({\mathbf{W}}_j{\mathbf{a}}_j))$$
因为每个角度条纹提取的通道权重可能会被局部噪声破坏，为此引入元素求和的快捷连接架构来降低局部噪声的影响：
$${\mathbf{o}}_j={\mathbf{a}}_j+{\mathbf{a}}_j\odot {\mathbf{d}}_j$$
${\mathbf{o}}_j$是重新赋权值后的输出，最后使用额外的卷积层来调整特征。

学习多粒度的特征

使用多数据流CNN作为特征提取器，改变SPT采样范围，网络能够利用全局图像的粗粒度特征以及局部图像的局部细粒度特征。公式7中的从$z_{i}to{\theta }_i$的映射到不同范围，因此可以获得变换图像的不同区域。类似于图4中b图的形式，用三种角度来转换这种映射。
$$\begin{gathered} f_1(z_i)=-2\pi \times z_i+\pi (a=\pi ,b=-\pi )提取全局特征 \\ {f}_2(z_i)=(-\frac{3}{4}\pi +\frac{1}{4}\pi )\times z_i-\frac{1}{4}\pi (a=-\frac{1}{4}\pi ,b=-\frac{3}{4}\pi ) \\ {f}_3(z_i)=(\frac{1}{4}\pi -\frac{3}{4}\pi )\times z_i+\frac{3}{4}\pi (a=\frac{3}{4}\pi ,b=\frac{1}{4}\pi )2,3提取局部特征 \end{gathered}$$
通过学习一系列函数f，可以得到不同的变换图，将这些图形作为输入提取多粒度的特征。

服装不变的特征学习

进一步挖掘在适度服装变化下同一个人的轮廓草图上的健壮服装不变曲线模式。训练中，把同一个人穿着不同衣服的图像视为具有相同的身份。对每个图像，$x_a^{i,j}$代表i-th stream的j-th branch,$x_p^{ij}$表示具有不同服装的相同身份的另一特征。$x_a^{i,j},x_p^{i,j}$通过softmax映射到以为同一性预测分布：
y i , j = s o f t m a x ( W i , j x i , j + b i , j ) , x i , j ∈ { x a i , j , x p i , j } ， \mathbf y^{i,j}=softmax(\mathbf W^{i,j}\mathbf x^{i,j}+\mathbf b^{i,j}),\mathbf x^{i,j} \in \{\mathbf x^{i,j}_a,\mathbf x^{i,j}_p\}， yi,j=softmax(Wi,jxi,j+bi,j),xi,j∈{xai,j​,xpi,j​}，
w和b分别代表最后一个全连接层的权重和偏差。使用交叉熵来进行误差比对y和gt值：
$${\mathcal{L}}_c^{i,j}=\sum _{c=1}^{\mathcal{C}}-g_c\log y_c^{i,j}=-\log y_t^{i,j}$$
t表示真实值标签。交叉熵损失没有明确考虑同一个人穿不同衣服的图像之间的关系。所以使用辅助三元组损失学习设计从锚点和正负样本的分支进行训练，他们表示锚的所有分支和流的串联特征，即正样本和负样本。减少组内差异和学习正对的共同潜在特征以及减轻负样本的特征。
$$\begin{gathered} d(\mathbf{x},\mathbf{y})=||\mathbf{x}-\mathbf{y}|{|}_2 \\ {\mathcal{L}}_t=\lfloor m+d({\mathbf{x}}_a,{\mathbf{x}}_p)-d({\mathbf{x}}_a,{\mathbf{x}}_n){\rfloor }_{+} \end{gathered}$$
m是三元组损失的边界。最后的损失可以表示为：
$$\mathcal{L}=\sum _{i=1}^S\sum _{j=1}^B{\mathcal{L}}_e^{i,j}+\eta {\mathcal{L}}_t$$
B是分支的分数，S是流的个数。在实验中，$m=5,\eta =10$.