图像降噪算法——DnCNN / FFDNet / CBDNet / RIDNet / PMRID / SID

1. 基本原理

这篇博客主要介绍几篇经典的CNN相关的图像降噪算法，其中DnCNN -> FFDNet -> CBDNet -> RIDNet -> PMRID我觉得这是一条越来越优的降噪网络主线，而SID是一个端到端的ISP网络，除了降噪还包含了demosaic等功能，因此单独列到最后。

1.1 DnCNN

Beyond a Gaussian Denoiser: Residual Learning of Deep CNN for Image Denoising
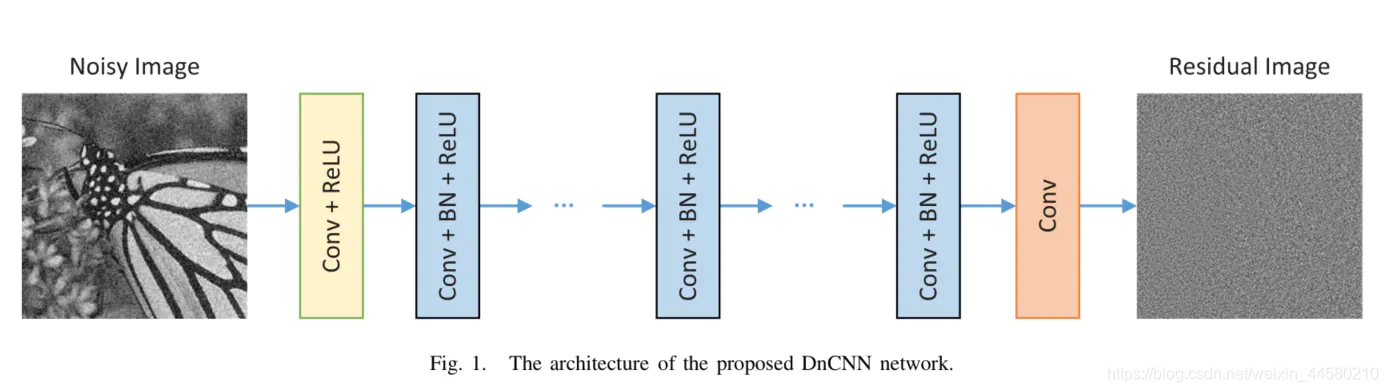
这篇论文算是使用CNN进行图像降噪最为经典的算法之一，算法并不复杂，但是在PSNR的指标上超过了BM3D，该算法框架如下图所示：

该网络的特点主要有：

1. 网络分为三部分，第一部分为Conv+Relu（一层），第二部分为Conv+BN+Relu（若干层），第三部分为Conv（一层），网络层数为17或者20层。
2. 网络学习的是图像残差，也就是带噪图像和无噪图像差值，损失函数采用的MSE。
3. 论文中强调了batch normalization的作用

1.2 FFDNet

FFDNet: Toward a Fast and Flexible Solution for CNN based Image Denoising
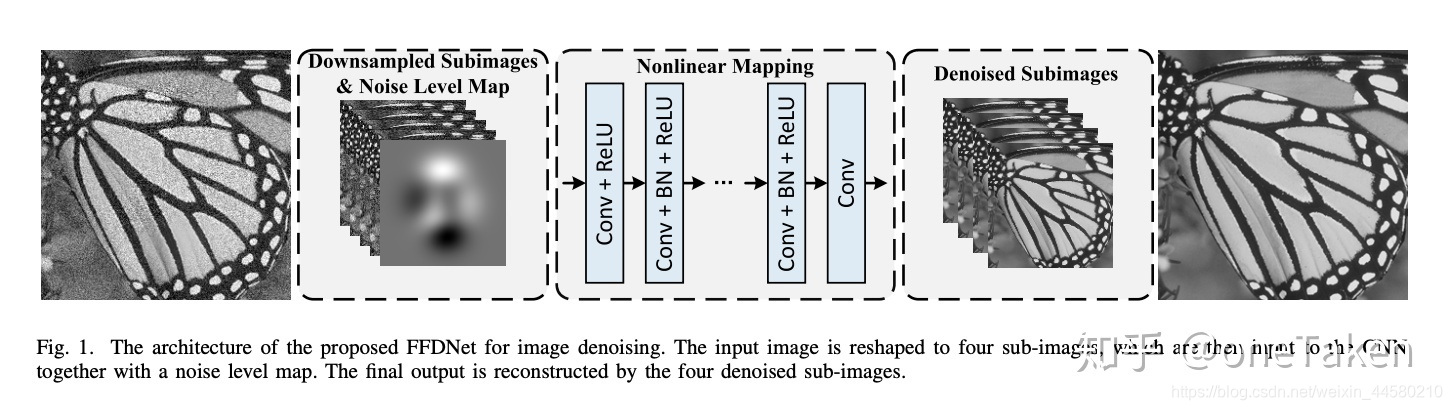
这篇论文是DnCNN的升级版，网络在对噪声的适应能力和计算量均要由于DnCNN，该算法网络结构如下：

该网络的特点主要有：

1. 该网络的结构和DnCNN一致，但是输入输出不同，网络输入为原始带噪图像降采样获得的四张子图以及一张由用户输入的参数$\sigma$生成的噪声水平图像，输出为四张降噪后的子图，通过上采样获得最终的降噪图像。使用的损失函数仍然是MSE。
2. 由于该网络的输入中包含一个有用户控制的参数，该算法对于不同噪声的适应程度要优于DnCNN

1.3 CBDNet

Toward Convolutional Blind Denoising of Real Photographs
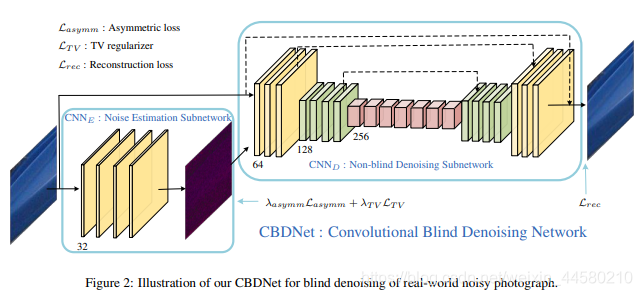
这篇论文算是FFDNet的再一次升级，在FFDNet中通过添加一个用户输入的噪声强度参数$\sigma$，在CBDNet中通过添加一个全卷积网络来学习该参数，从而达到自适应噪声的目的，该算法的网络结构如下：

该网络的特点主要有：

1. 该网络的结构分为两部分：第一部分为五层全卷积网络用于噪声估计噪声水平图，第二部分与FFDNet不同，为带残差的UnNet，用于降噪。

2. 设计了非对称损失函数，目的主要是为了消除非对称敏感性，所谓非对称敏感性指的像BM3D和FFDNet这样的降噪算法，输入降噪参数$\sigma$较小时，降噪效果较差，输入降噪参数$\sigma$较大时，虽然纹理有损失，但是降噪效果仍然比较好。给定像素$i$的估计水平$\hat{\sigma }(y_i)$和真实值$\sigma (y_i)$，当$\hat{\sigma }(y_i)<\sigma (y_i)$时，应该对MSE引入更多的惩罚，因此：$${\mathcal{L}}_{\text{asymm }}=\sum _i\left|\alpha -{\mathbb{I}}_{\left(\hat{\sigma }\left(y_i\right)-\sigma \left(y_i\right)\right)<0}\right|\cdot {\left(\hat{\sigma }\left(y_i\right)-\sigma \left(y_i\right)\right)}^2$$当$e<0$时，${\mathbb{I}}_e=1$，否则为0。如果设定$0<\alpha <0.5$，则可以对低估误差引入更多的惩罚。同时引入全变分正则项约束$\hat{\sigma }(y)$的平滑性：$${\mathcal{L}}_{TV}={\Vert {\nabla }_h\hat{\sigma }(y)\Vert }_2^2+{\Vert {\nabla }_v\hat{\sigma }(y)\Vert }_2^2$$最后一部分就是MSE：$${\mathcal{L}}_{rec}=\Vert \hat{x}-x{\Vert }_2^2$$综上所述，整个CBDNet的目标损失函数为：$$\mathcal{L}={\mathcal{L}}_{rec}+{\lambda }_{asymm}{\mathcal{L}}_{asymm}+{\lambda }_{TV}{\mathcal{L}}_{TV}$$

3. 该算法学习的是更接近于真实噪声的高斯泊松噪声，而前面两篇论文都是学习高斯噪声；并且结合使用合成和真实噪声数据来训练模型，提高模型泛化能力，可以更好地对真实场景进行降噪；

1.4 RIDNet

Real Image Denoising with Feature Attention
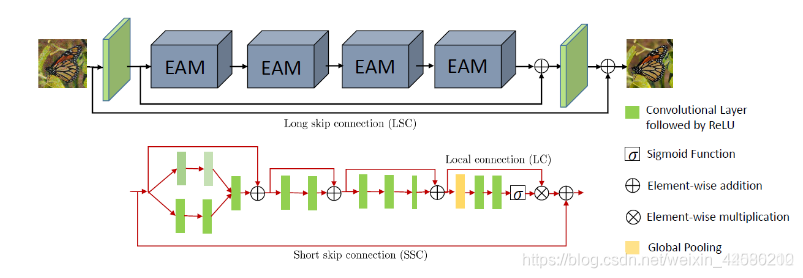
这篇论文效果比CBDNet要更好，应该算目前降噪效果最好的算法了，论文中指出CBDNet是一个二阶段去噪网络，不够高效灵活，而本文的一阶段算法更加实用，可以在标准差已知或者未知的情况下同时处理高斯泊松噪声，网络结构如下：

该网络的特点主要有：

1. 这个网路的结构设计得相对复杂，主要包括三部分：特征提取、4个EMA组成的残差模型、重建。其中特征提取和重建模块都是卷积层+ReLU层。EMA的结构如上图中下半部分框图所示：
   （1）首先是两个空洞卷积分支，用来增加感受野，然后进行拼接并进行卷积融合
   （2）然后是两个类似残差学习的结构，用于进行特征的提取
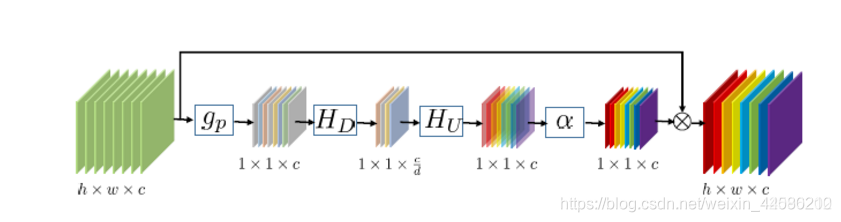
   （3）最后是注意力机制，主要由一系列1x1的卷积核构成（这个注意力机制我还不太理解是怎么回事，后面再花时间研究下），结构如下图所示：
   
2. 该网络的损失函数为L1损失函数： $$L(\mathcal{W})=\frac{1}{N}\sum _{i=1}^N{\Vert \mathrm{RIDNet}\left(x_i\right)-y_i\Vert }_1$$

1.5 PMRID

Practical Deep Raw Image Denoising on Mobile Devices
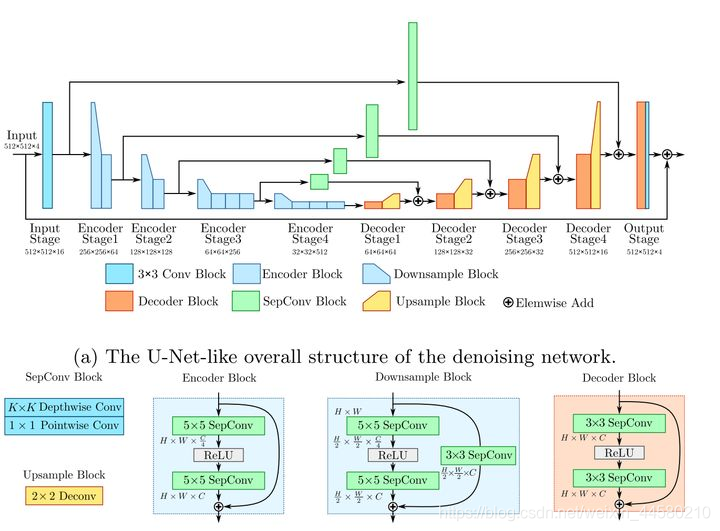
这篇论文是2020 CVPR上旷视提出来的一篇非常elegant的算法，该算法的特点网络结构比较小，通过一个k-sigma变换来解决小网络在不同增益噪声下的鲁棒性问题，网络结构如下图所示：
该网络的主要特点有：

1. 这个网络的结构大体上还是一个UNet的结构，为了降低计算量使用了separable conv卷积，然后使用的是5x5的模型来降低模型深度，使用stride为2的卷积进行下采样，以及2x2的deconv结构进行上采样，使用3x3的separable conv来进行skip connnection的通道构建。可以说网络结构是小而精美。
2. 该论文我觉得最有启示的一点是提出了k-sigma变换，像FFDNet，CBDNet都是通过设置网络参数来适应不同强度的噪声，而本文是通过将不同强度的噪声进行归一化来简化网络结构，这个思路有点类似于generalization anscombe transform，不了解的同学可以了解下，下面我们来简单进行下k-simga变换的推导，首先是CMOS Sensor的成像模型入下图所示：
   理想像素值$x^{\ast }$和实际像素值$x$的计算分别如下所示：
   $$x^{\ast }=g\alpha u^{\ast }$$$$x=g\left(\alpha u+n_d\right)+n_r$$其中，由于光子服从波粒二象性，因此服从如下高斯分布$$u\sim P\left(u^{\ast }\right)$$暗电流噪声服从$$n_d\sim N\left(0,{\sigma }_d^2\right)$$读出噪声服从$$n_r\sim N\left(0,{\sigma }_r^2\right)$$因此整体满足高斯泊松分布$$x\sim (g\alpha )P\left(\frac{x^{\ast }}{g\alpha }\right)+N\left(0,g^2{\sigma }_d^2+{\sigma }_r^2\right)$$我们令$k=g\alpha$，${\sigma }^2=g^2{\sigma }_d^2+{\sigma }_r^2$则有$$x\sim kP\left(\frac{x^{\ast }}{k}\right)+N\left(0,{\sigma }^2\right)$$这是$x$的均值和方差分别为$$E(x)=x^{\ast }$$$$\mathrm{Var}(x)=k{x}^{\ast }+{\sigma }^2$$接下就是k-sigma变换的公式：$$f(x)=\frac{x}{k}+\frac{{\sigma }^2}{k^2}$$经过k-sigma变换后，$f(x)$满足$$f(x)\sim \mathcal{P}\left(\frac{x^{\ast }}{k}\right)+\mathcal{N}\left(\frac{{\sigma }^2}{k^2},\frac{{\sigma }^2}{k^2}\right).$$我们将泊松分布$\mathcal{P}$近似是哟啊那个高斯分布$\mathcal{N}(\lambda ,\lambda )$代替，则有$$\begin{array}{rl}& P\left(\frac{x^{\ast }}{k}\right)+\mathcal{N}\left(\frac{{\sigma }^2}{k^2},\frac{{\sigma }^2}{k^2}\right)\\ \approx & \mathcal{N}\left(\frac{x^{\ast }}{k},\frac{x^{\ast }}{k}\right)+\mathcal{N}\left(\frac{{\sigma }^2}{k^2},\frac{{\sigma }^2}{k^2}\right)\\ =& \mathcal{N}\left(\frac{x^{\ast }}{k}+\frac{{\sigma }^2}{k^2},\frac{x^{\ast }}{k}+\frac{{\sigma }^2}{k^2}\right)\\ =& \mathcal{N}\left[f\left(x^{\ast }\right),f\left(x^{\ast }\right)\right]\end{array}$$使用标定的k和sigma按照k-sigma公式变换后，原始的噪声分布就只和没有噪声的数据$x^{\ast }$有关，因此就可以避免不同增益下噪声不同带来的负担。

1.6 SID

Learning to See in the Dark
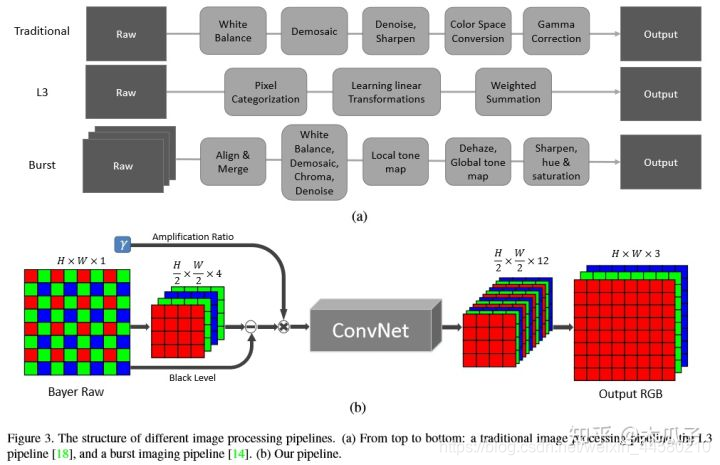
这篇论文除了提供一个非常有用的数据集之外，还提出了一个端到端的网络结果，直接处理Raw数据得到去马赛克，去噪和色彩变化后的图像，网络结果如下：

该网络的特点主要有：

1. 输入为bayer图拆分出来的4通道数据，分辨率变为原来的一半，输出为12通道的数据，分辨率为原图的一般，然后经过sub-pixel复原全分辨率的RGB三通道数据，其中ConvNet默认是一个UNet的数据结构。
2. 损失函数使用L1的损失函数，因此降噪的结果显得比较平滑。
3. 该网络并没有专门的设计降噪网络，因此降噪效果并不是特别出色，但是其在颜色复原上会有较为明显的优势，并且该网络泛化能力差，一款相机得单独训练一个网络。

2. pytorch代码

以上说的所有的网络模型都是可以下载到源码的，其中一部分我在pytorch上进行过训练和测试，这里我基于pytorch写了一份用于PMRID训练和测试的代码，欢迎参考Jichao-Peng/PMRID-Pytorch

3. 结论

最近几年的顶会CNN的降噪方法已经完全占据了主流，实验也确实证明了CNN的降噪算法相对传统算法在一些方面的优势，我自己也确实被CNN方法给惊艳到了，之后再慢慢深入学习补充

此外，这里我写一个各种算法的总结目录图像降噪算法——图像降噪算法总结，对图像降噪算法感兴趣的同学欢迎参考