1 基本概述
CLAHE是一个比较有意思的图像增强的方法,主要用在医学图像上面。之前的比赛中,用到了这个,但是对其算法原理不甚了解。在这里做一个复盘。
CLAHE起到的作用简单来说就是增强图像的对比度的同时可以抑制噪声
CLAHE的英文是Contrast Limited Adaptive Histogram Equalization 限制对比度的自适应直方图均衡。在学习这个之前,我们要先学习一下下面的前置算法:
- 【Contrast Stretching】:对比度拉伸;
- 【HE】:直方图均衡;
- 【CLHE】:对比度限制的HE
- 【AHE】:自适应直方图均衡化
2 竞赛中的CLAHE实现
在比赛中,我们往往使用albumentations库函数进行图像的预处理,因为这个预处理库的运行速度非常的快,而且封装了大量的图像增强的方法。图像任务的话这个库函数非常滴奈斯。
本文中会介绍一下albumentations库函数实现CLAHE的代码,然后再用openCV实现。
import albumentations
RESIZE_SIZE = 1024 # or 768
train_transform = albumentations.Compose([
albumentations.Resize(RESIZE_SIZE, RESIZE_SIZE),
albumentations.OneOf([
albumentations.RandomGamma(gamma_limit=(60, 120), p=0.9),
albumentations.RandomBrightnessContrast(brightness_limit=0.2, contrast_limit=0.2, p=0.9),
albumentations.CLAHE(clip_limit=4.0, tile_grid_size=(4, 4), p=0.9),
]),
albumentations.HorizontalFlip(p=0.5),
albumentations.ShiftScaleRotate(shift_limit=0.2, scale_limit=0.2, rotate_limit=20,
interpolation=cv2.INTER_LINEAR, border_mode=cv2.BORDER_CONSTANT, p=1),
albumentations.Normalize(mean=(0.485, 0.456, 0.406), std=(0.229, 0.224, 0.225), max_pixel_value=255.0, p=1.0)
])
这是一个图像增强的pipline,其中的流程是:
- Resize就是拉伸图片修改尺寸
- RandomGamma就是使用gamma变换
- RandomBrightnessContrast就是随机选择图片的对比度和亮度
- CLAHE是一种对比度受限情况下的自适应直方图均衡化算法
- HorizontalFlip水平翻转
- ShiftScaleRotate这个就是平移缩放旋转三合一,给力!
- Normalize这个就是图像归一化了。
本文主要讲解的就是CLAHE这个直方图均衡化的算法。
3 openCV绘制直方图
使用openCV的代码来获取一个图片的灰度直方图:
import cv2
import numpy as np
import matplotlib.pyplot as plt
def plot(grayHist):
plt.plot(range(256), grayHist, 'r', linewidth=1.5, c='red')
y_maxValue = np.max(grayHist)
plt.axis([0, 255, 0, y_maxValue]) # x和y的范围
plt.xlabel("gray Level")
plt.ylabel("Number Of Pixels")
plt.show()
if __name__ == "__main__":
# 读取图像并转换为灰度图
img = cv2.imread(r'E:\dog.jpg', 0)
# 图像的灰度级范围是0~255
grayHist = cv2.calcHist([img], [0], None, [256], [0, 256])
# 绘制直方图
plot(grayHist)
狗子的图片就是左边的这个,发现灰度值在100左右的像素个数最多:
4 对比度Contrast
在生活中,我们在PS图片的时候,往往会用到图片对比度,那么这个究竟是什么东西呢?
图片对比度指的是一幅图片中最亮的白和最暗的黑之间的反差大小。常用的定量度量方法是Michelson对比度:
C
=
I
m
a
x
−
I
m
i
n
I
m
a
x
+
I
m
i
n
C = \frac{I_{max}-I_{min}}{I_{max}+I_{min}}
C=Imax+IminImax−Imin
- 当一幅图像最白和最黑像素灰度都是128时,图像对比度最低,C=0;
- 当一幅图像最白像素灰度=255,最黑像素灰度=0时,图像对比度最高,C=1.0。
【英文中如何描述高对比度与低对比度的?】
当一幅图像最白和最黑像素灰度都在128附近浮动时,图像的直方图集中在中间的几个桶,图像看起来灰蒙蒙的,英语中使用dull描述这种效果。相反,如果图像中黑白像素的跨度较大,则图像富有通透感,英语中使用clarity描述这种效果。
图片中左边的图片就是dull,灰度直方图也是集中在中间区域,这就是低对比度;最右边的图片是clarity,直方图感觉是被拉开了、舒展了,这就是高对比度。
5 Contrast Stretching
我们已经搞懂了图片不通透的原因,就是灰度直方图不够舒展,集中在了一个小区域,这样我们可以通过数学的方法把低对比度的图像提高对比度。最简单的方法就是对比度拉伸(Contrast Stretching)。
现在有这样的一个低对比度的图片,其灰度直方图集中在中间的区域。然后我们想把这个灰度直方图拉伸到整个0~255的区间,我们怎么做呢?(这里假设这个低对比度的图片的灰度集中在100到200之间好了)
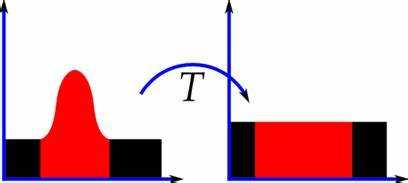
用一个这样的分段线性函数,来处理上面那个低对比度图片的时候,可以把(r2,s2)极端的设置成(100,0),把(r3,s3)设置成(200,255),这样把原来的直方图通过这个函数映射,其实就是把100~200范围线性拉伸到0~255这么大。
这种方法最简单,简单的说就是线性拉伸直方图。对于某些图片可以起到效果:
但是对于比较复杂的图片,并没有什么效果:
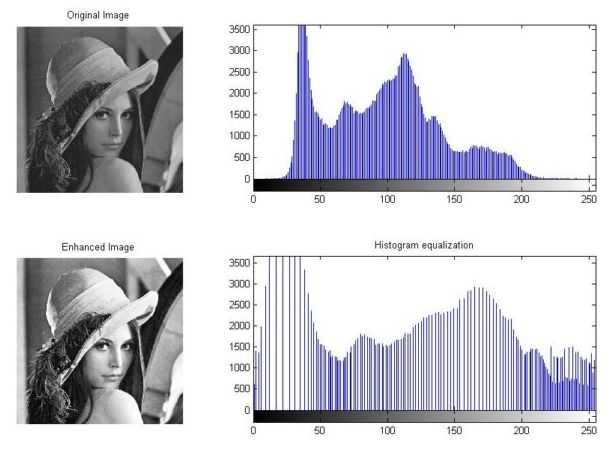
6 Histogram Equalization
对比度解决不了的问题,我们来用HE试试。Histogram Equalization的思想就是用数学方法重新调整像素的亮度分布,来保证直方图具有最大的动态范围,也就是尽可能地让灰度直方图是一个矩形!
其实Contrast Stretching也是做的一样的事情,只是它用的简单的分段线性函数来重新映射灰度,现在用更巧妙地方法。
【定义一些数学符号】
- p ( x ) p(x) p(x):调整之前的直方图的概率密度函数
- q ( y ) q(y) q(y):调整之后的直方图的概率密度函数,可以看出来,是一个常数,所以用C来表示
因为**不管怎么转换,概率密度函数的累积总是1,而转换前后的取值范围都是[0,1],**所以可以得到:
∫
0
1
p
(
x
)
d
x
=
∫
0
1
C
d
y
=
1
\int_0^1{p(x)dx=\int_0^1Cdy=1}
∫01p(x)dx=∫01Cdy=1
(当然,这里可以很快的算出来,C=1)
**我们希望找到,一个x和y的映射关系,也就是
y
=
f
(
x
)
y=f(x)
y=f(x),**不难想到,这个
f
(
x
)
f(x)
f(x)就应该是
p
(
x
)
p(x)
p(x)的累积分布函数,也就是:
f
(
x
)
=
∫
0
x
p
(
u
)
d
u
f(x)=\int_0^xp(u)du
f(x)=∫0xp(u)du
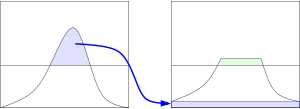
这个图中,直观的展示了,任何一个直方图,只要按照该直方图的累积分布函数进行拉伸,就可以得到一个矩形的直方图。
下面是一个利用这样的方法增强对比度的例子:
可以发现,在直方图密集的地方,就会被拉的松散
再看另外一个例子:
可以发现,使用HE之后的直方图的累积分布函数,是一个直线
7 CLAHE
HE算法在一种情况下,效果不好,**如果一个图片中有大块的暗区或者亮区的话,效果非常不好。**这个的原因,也非常好理解,因为HE其实要求一个图片中必须有10%的最亮的像素点,必须有10%第二亮的像素点,必须有10%第三亮的像素点……假设有一张纯黑的图片,你想想经过HE处理之后,会出现什么情况?答案就是一部分黑的像素也会被强行搞成白的
下面是一个例子,发现经过HE之后的图片出现了大量噪点:
【Histogram Equalization的缺点】
- 对于灰度非常集中的区域,直方图会被拉的非常稀疏,从而导致对比度增强过大,成为噪音;
- 一些区域调整后丢失细节
7.1 Contrast Limited HE
针对第一个问题,提出了CLHE,加入对比度限制,其实原理很简单置直方图分布的阈值,将超过该阈值的分布“均匀”分散至概率密度分布上,由此来限制转换函数(累计直方图)的增幅。
这样的话,直方图就不会出现概率密度函数过大的区域,从而避免了某些集中区域被拉得过于系数。
7.2 Adaptive HE
Adaptive HE的基本思想是将原始图片划分成子区域,然后对每个子区域进行HE变换。当然,这样做的问题应该是显而易见的:
每一块区域之间都会有非常大的不连续。因此为了解决这个问题,提出了优化方案双线性插值的AHE,然后这个基础上再使用CLHE的截断对比度的思想,就变成了我们现在的CLAHE算法。
【使用双线性插值的方案】
-
将图像分为多个矩形块大小,对于每个矩形块子图,分别计算其灰度直方图和对应的变换函数(累积直方图)
-
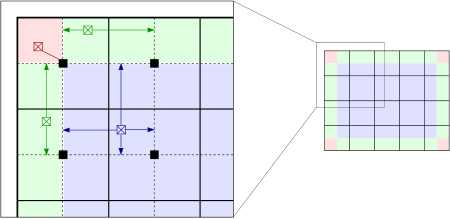
将原始图像中的像素按照分布分为三种情况处理:
- 红色区域中的像素按照其所在子图的变换函数进行灰度映射
- 绿色区域中的像素按照所在的两个相邻子图变换函数变换后进行线性插值得到
- 紫色区域中的像素按照其所在的四个相邻子图变换函数变换后双线性插值得到
8 结果对比与openCV实现
【这里是openCV实现HE的方法】
img = cv.imread(r'E:\dog.jpg', 0)
equ = cv.equalizeHist(img) # 输入为灰度图
res = np.hstack((img, equ)) # stacking images side-by-side
cv.imwrite('res.png',res)
运行结果:
【openCV实现CLAHE】
img = cv2.imread(r'E:\dog.jpg', 0)
# create a CLAHE object
clahe = cv2.createCLAHE(clipLimit=2.0, tileGridSize=(8,8))
cl1 = clahe.apply(img)
res = np.hstack((img, cl1))
cv2.imwrite('res.jpg', res)
【更多对比的例子】
- 左边是原图
- 中间是HE,有过亮过暗的区域;
- 右边是CLAHE,没有过亮过暗的区域。
然后我在另外一个博文,找到了上面那个例子的彩色版本哈哈:
参考文章:
- https://zhuanlan.zhihu.com/p/98541241
- https://blog.csdn.net/lwx309025167/article/details/103770834
- https://blog.csdn.net/u013066730/article/details/82970380
- https://www.cnblogs.com/imageshop/archive/2013/04/07/
- http://helloworld2020.net/393/