动态规划问题解决的基本思想:
1、根绝问题所求的那一项和变量的个数,确定是一维数组,二维数组或者多维数组。
2、写出初始值,一般是某个变量为1或者0 的特殊情况时候的解。
3、通过循环,一般是两个循环中间每一层循环表示一个变量的递增情况。
4、在循环中间写出对应的递推关系表达式,求出问题的每一项。
5、根据题意得到答案,一般是数组的最后一项。
提示 : 找递推关系是动态规划最难的一步,所以不要懒
一、走方格问题
1.问题引入:
有一个矩阵map,它每个格子有一个权值。从左上角的格子开始每次只能向右或者向下走,最后到达右下角的位置,路径上所有的数字累加起来就是路径和,返回所有的路径中最小的路径和。给定一个矩阵map及它的行数n和列数m,请返回最小路径和。保证行列数均小于等于100.
输入输出样例:
第一行,输入n,m表示这个矩阵的行数和列数,接下来的n行,输入每行的m个数字,也即每个格子的权值。最后输出最小路径和。如:
2 3
1 2 3
1 1 1
输出:4
2.思路分析 :
因为只能向右和向下,所以从第一个格子到某个格子(不在第一排也不在第一列,否则没有编程的必要了)的最短距离只与第一个格子到它左边格子的最短距离以及第一个格子到它上面格子的最短距离这两个值有关,取这两个值中的较小者。可以设dp[n][m]为走到n*m位置的最短路径长度,则dp[n][m] = Min(dp[n-1][m],dp[n][m-1]),这就运用到了动态规划的思想。题目要求算出复杂情况的值,而动态规划则是算出几个简单的作为已知值,然后找规律由后往前推理。
3.代码如下:
#include<stdio.h>
#include<stdlib.h>
int a[100][100];
int dp[100][100];
int Min(int a,int b){
if(a<b){
return a;
}else{
return b;
}
}
int getMin(int m,int n){
int min;
dp[0][0]=a[0][0];
for(int i=1;i<m;i++){
dp[i][0]=a[i][0]+dp[i-1][0];
}
for(int i=1;i<n;i++){
dp[0][i]=a[0][i]+dp[0][i-1];
}
for(int i=1;i<m;i++){
for(int j=1;j<n;j++){
min=Min(dp[i-1][j],dp[i][j-1]);
dp[i][j]=min+a[i][j];
}
}
return dp[m-1][n-1];
}
int main(){
int m,n;
scanf("%d%d",&m,&n);
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
scanf("%d",&a[i][j]);
}
}
printf("%d\n",getMin(m,n));
return 0;
}
二、最长公共序列数问题
1.问题引入:
给定两个字符串A和B,返回两个字符串的最长公共子序列的长度。例如,A="1A2C3D4B56”,B="B1D23CA45B6A”,”123456"或者"12C4B6"都是最长公共子序列。给定两个字符串A和B,同时给定两个串的长度n和m,请返回最长公共子序列的长度。保证两串长度均小于等于300。测试样例:第一行输入一个字符串,第二行输入这个字符串的长度,第三行和第四行也分别输入一个字符串和这个字符串的长度。最后输出结果。如:1A2C3D4B56
10
B1D23CA45B6A
12返回:6
2.思路分析:
设dp[n][m] ,为A的前n个字符与B的前m个字符的公共序列长度,则当A[n]==B[m]的时候,dp[i][j] =
max(dp[i-1][j-1]+1,dp[i-1][j],dp[i][j-1]),否则,dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1]);
3.代码如下:
#include<stdio.h>
#include<string.h>
int dp[100][100];
int Max(int a,int b,int c){
int max=a;
if(b>max){
max=b;
}
if(c>max){
max=c;
}
return max;
}
int getMax(char s1[],char s2[],int m,int n){
int i,j;
for(i=0;i<m;i++){ //当 s2取 1个的时候 ,s1为可变长度
if(s1[i]==s2[0]){
dp[i][0]=1;
for(j=i+1;j<m;j++){
dp[j][0]=1;
}
break;
}
}
for(i=0;i<n;i++){ //当 s1取 1个的时候 ,s2为可变长度
if(s2[i]==s1[0]){
dp[0][i]=1;
for(j=i+1;j<n;j++){
dp[0][j]=1;
}
break;
}
}
for(i=1;i<m;i++){
for(j=1;j<n;j++){
if(s1[i]==s2[j]){
dp[i][j]=Max(dp[i-1][j-1]+1,dp[i-1][j],dp[i][j-1]);
}else{
dp[i][j]=dp[i-1][j]>=dp[i][j-1]?dp[i-1][j]:dp[i][j-1];
}
}
}
return dp[m-1][n-1];
}
int main(){
int m,n;
char s1[100];
char s2[100];
gets(s1);
gets(s2);
m=strlen(s1);
n=strlen(s2);
printf("%d\n",getMax(s1,s2,m,n));
return 0;
}
三、密码脱落
1.问题引入:
X星球的考古学家发现了一批古代留下来的密码。
这些密码是由A、B、C、D 四种植物的种子串成的序列。
仔细分析发现,这些密码串当初应该是前后对称的(也就是我们说的镜像串)。
由于年代久远,其中许多种子脱落了,因而可能会失去镜像的特征。
你的任务是:
给定一个现在看到的密码串,计算一下从当初的状态,它要至少脱落多少个种子,才可能会变成现在的样子。
输入一行,表示现在看到的密码串(长度不大于1000)
要求输出一个正整数,表示至少脱落了多少个种子。
例如,输入:
ABCBA
则程序应该输出:
0
再例如,输入:
ABDCDCBABC
则程序应该输出:
3
2.思路分析:
这道题一定要明白回文构成的颠倒现象,可以用两个字符串去实现,一个是原字符串,另一个则是源字符串反过来的字符串,只要匹配两者的最大的相同序列,用长度减去即可求得答案。
3.代码如下:
#include<stdio.h>
#include<string.h>
int dp[100][100];
int Max(int a,int b,int c){
int max=a;
if(b>max){
max=b;
}
if(c>max){
max=c;
}
return max;
}
int getMax(char s1[],char s2[],int m){
int i,j;
for(i=0;i<m;i++){
if(s1[0]==s2[i]){
dp[0][i]=1;
for(j=i+1;j<m;j++){
dp[0][j]=1;
}
break;
}
}
for(int i=0;i<m;i++){
if(s1[i]==s2[0]){
dp[i][0]=1;
for(j=i+1;j<m;j++){
dp[j][0]=1;
}
break;
}
}
for(i=1;i<m;i++){
for(j=1;j<m;j++){
if(s1[i]==s2[j]){
dp[i][j]=Max(dp[i-1][j-1]+1,dp[i-1][j],dp[i][j-1]);
}else{
dp[i][j]=dp[i-1][j]>=dp[i][j-1]?dp[i-1][j]:dp[i][j-1];
}
}
}
return m-dp[m-1][m-1];
}
int main(){
int m,n;
char s1[100];
char s2[100];
gets(s1);
m=strlen(s1);
for(n=0;n<m;n++){
s2[n]=s1[m-n-1];
}
printf("%d\n",getMax(s1,s2,m));
return 0;
}
四、硬币凑数问题
1.问题引入:
假设现在有面值为1元、3元和5元的硬币若干枚,如何用最少的硬币凑够需要的钱数。现输入一个数,表示需要的钱数,要求输出一个整数表示最小的硬币数。
2.思路分析:
动态规划算法广泛地用于最优化问题中,在我们从 1 元开始依次找零时,可以尝试一下当前要找零的面值(这里指 1 元)是否能够被分解成另一个已求解的面值的找零需要的硬币个数再加上这一堆硬币中的某个面值之和,如果这样分解之后最终的硬币数是最少的,那么问题就得到答案了。这就是动态规划的思想。
3.代码如下:
#include<stdio.h>
int min[10000];
int kinds[]={5,2,1};
int f(int n,int m){
min[0]=0;
min[1]=1;
for(int i=2;i<m+1;i++){
int a=m;
for(int j=0;j<n;j++){
if(kinds[j]<=i){
int t=min[i-kinds[j]]+1;
a=a<t?a:t;
}
}
min[i]=a;
}
return min[m];
}
int main(){
int m;
scanf("%d",&m);
printf("%d\n",f(3,m));
return 0;
}
五、K好数
1.问题描述
如果一个自然数N的K进制表示中任意的相邻的两位都不是相邻的数字,那么我们就说这个数是K好数。求L位K进制数中K好数的数目。例如K = 4,L = 2的时候,所有K好数为11、13、20、22、30、31、33 共7个。由于这个数目很大,请你输出它对1000000007取模后的值。
输入包含两个正整数,K和L。
对于30%的数据,KL <= 106;
对于50%的数据,K <= 16, L <= 10;
对于100%的数据,1 <= K,L <= 100。
2.思路:
第i位数放置j所得到的所有K好数由i-1进制数的所有K好数之和去除与j相邻的两种情况求得。
3.代码如下:#include<stdio.h>
int dp[100][100];
int getAns(int k,int l){
int i,j,t,sum=0;
for(i=0;i<k;i++){
dp[1][i]=1;
}
for(i=2;i<=l;i++){
for(j=0;j<k;j++){
for(t=0;t<k;t++){
if(t!=j-1&&t!=j+1){
dp[i][j]+=dp[i-1][t];
}
}
}
dp[i][j]%=100000008;
}
for(j=1;j<k;j++){
sum=sum+dp[l][j];
sum%=100000008;
}
return sum;
}
int main(){
int k,l;
scanf("%d%d",&k,&l);
printf("%d\n",getAns(k,l));
return 0;
}
#include<stdio.h>
int dp[100][100];
int getAns(int k,int l){
int i,j,t,sum=0;
for(i=0;i<k;i++){
dp[1][i]=1;
}
for(i=2;i<=l;i++){
for(j=0;j<k;j++){
for(t=0;t<k;t++){
if(t!=j-1&&t!=j+1){
dp[i][j]+=dp[i-1][t];
}
}
}
dp[i][j]%=100000008;
}
for(j=1;j<k;j++){
sum=sum+dp[l][j];
sum%=100000008;
}
return sum;
}
int main(){
int k,l;
scanf("%d%d",&k,&l);
printf("%d\n",getAns(k,l));
return 0;
}六、01背包问题
1.问题引入:
有编号分别为a,b,c,d,e的五件物品,它们的重量分别是2,2,6,5,4,它们的价值分别是6,3,5,4,6,现在给你个承重为10的背包,如何让背包里装入的物品具有最大的价值总和?
2.思路分析:
name weight value 1 2 3 4 5 6 7 8 9 10 a 2 6 0 6 6 9 9 12 12 15 15 15 b 2 3 0 3 3 6 6 9 9 9 10 11 c 6 5 0 0 0 6 6 6 6 6 10 11 d 5 4 0 0 0 6 6 6 6 6 10 10 e 4 6 0 0 0 6 6 6 6 6 6 6
通过找规律手工填写出上面这张表就能理解背包的动态规划算法了。状态转移方程为:
f[i,j] = Max{ f[i-1,j-Wi]+Pi( j >= Wi ),//表示第i件物品放入
f[i-1,j] //表示第i件物品不放入}
| name | weight | value | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| a | 2 | 6 | 0 | 6 | 6 | 9 | 9 | 12 | 12 | 15 | 15 | 15 |
| b | 2 | 3 | 0 | 3 | 3 | 6 | 6 | 9 | 9 | 9 | 10 | 11 |
| c | 6 | 5 | 0 | 0 | 0 | 6 | 6 | 6 | 6 | 6 | 10 | 11 |
| d | 5 | 4 | 0 | 0 | 0 | 6 | 6 | 6 | 6 | 6 | 10 | 10 |
| e | 4 | 6 | 0 | 0 | 0 | 6 | 6 | 6 | 6 | 6 | 6 | 6 |
通过找规律手工填写出上面这张表就能理解背包的动态规划算法了。状态转移方程为:
f[i,j] = Max{ f[i-1,j-Wi]+Pi( j >= Wi ),//表示第i件物品放入
f[i-1,j] //表示第i件物品不放入}
首先要明确这张表是至底向上,从左到右生成的。
为了叙述方便,用e2单元格表示e行2列的单元格,这个单元格的意义是用来表示只有物品e时,有个承重为2的背包,那么这个背包的最大价值是0,因为e物品的重量是4,背包装不了。
对于d2单元格,表示只有物品e,d时,承重为2的背包,所能装入的最大价值,仍然是0,因为物品e,d都不是这个背包能装的。
同理,c2=0,b2=3,a2=6。
对于承重为8的背包,a8=15,是怎么得出的呢?
在这里,
f[i-1,j]表示我有一个承重为8的背包,当只有物品b,c,d,e四件可选时,这个背包能装入的最大价值
f[i-1,j-Wi]表示我有一个承重为6的背包(等于当前背包承重减去物品a的重量),当只有物品b,c,d,e四件可选时,这个背包能装入的最大价值
f[i-1,j-Wi]就是指单元格b6,值为9,Pi指的是a物品的价值,即6
由于f[i-1,j-Wi]+Pi = 9 + 6 = 15 大于f[i-1,j] = 9,所以物品a应该放入承重为8的背包
3.代码如下:
#include<stdio.h>
int v[]={6,3,5,4,6};
int w[]={2,2,6,5,4};
int dp[100][100];
int Max(int a,int b){
if(a>=b){
return a;
}else{
return b;
}
}
int getAns(int i,int wi){
for(int x=0;x<=i;x++){
dp[x][0]=0;
}
for(int x=0;x<=wi;x++){
dp[0][x]=0;
}
for(int x=1;x<=i;x++){
for(int y=1;y<=wi;y++){
if(y>=w[x-1]){
dp[x][y]=Max(dp[x-1][y],v[x-1]+dp[x-1][y-w[x-1]]);
}else{
dp[x][y]=dp[x-1][y];
}
printf("%4d",dp[x][y]);
}
printf("\n");
}
return dp[i][wi];
}
int main(){
int max=getAns(5,10);
printf("%d\n",max);
return 0;
}
七、有向五环图最短路径问题
1.问题引入:
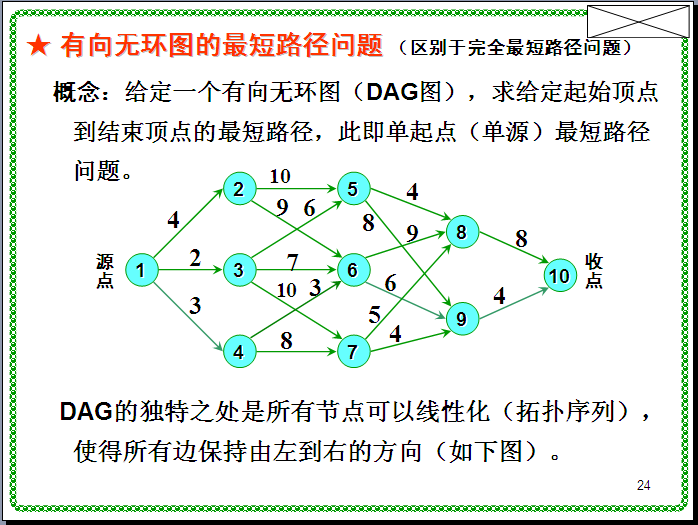
2.思路分析:

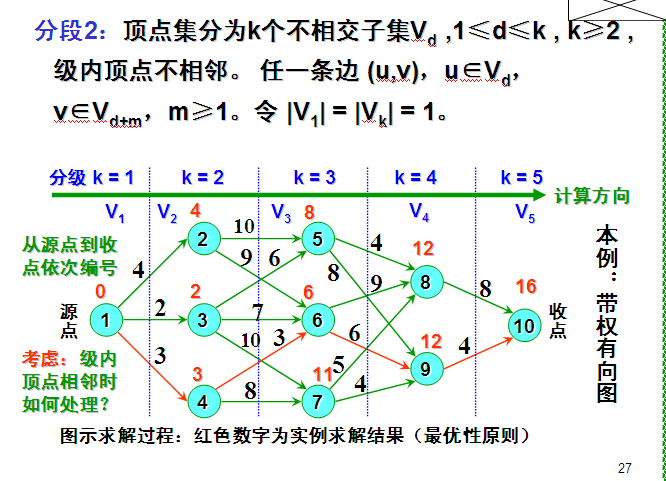
3.代码如下:
#include<stdio.h>
#define x 9999;
#define max 9999;
int dist[10];
void f(int a[][11]){
int i,j,k;
dist[0]=0;
for(i=1;i<10;i++){
k=max;
for(j=0;j<i;j++){
if(a[j][i]!=0){
if(dist[j]+a[j][i]<k){
k=dist[j]+a[j][i];
}
dist[i]=k;
}
}
}
}
int main(){
int i;
int a[][11] = { { 0, 4, 2, 3, 0, 0, 0, 0, 0, 0 },
{ 0, 0, 0, 0, 10, 9, 0, 0, 0, 0 },
{ 0, 0, 0, 0, 6, 7, 10, 0, 0, 0 },
{ 0, 0, 0, 0, 0, 3, 8, 0, 0, 0 },
{ 0, 0, 0, 0, 0, 0, 0, 4, 8, 0 },
{ 0, 0, 0, 0, 0, 0, 0, 9, 6, 0 },
{ 0, 0, 0, 0, 0, 0, 0, 5, 4, 0 },
{ 0, 0, 0, 0, 0, 0, 0, 0, 0, 8 },
{ 0, 0, 0, 0, 0, 0, 0, 0, 0, 4 },
{ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 } };
f(a);
printf("%d\n",dist[9]);
} 