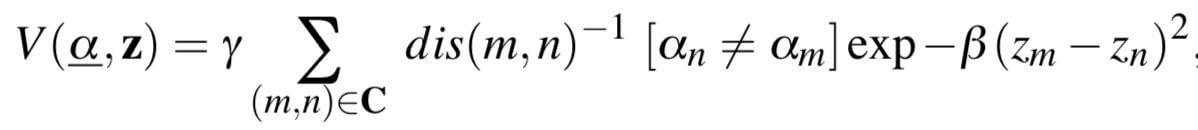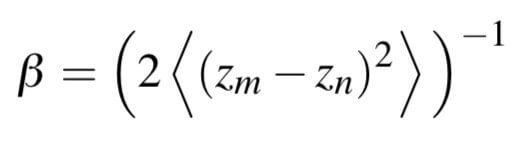【图像分割】GrabCut算法

1.常见的图像分割方法比较

Magic Wand：从用户指定的像素点（或者区域）开始计算与之连接的像素的所属区域，并使得所有选择的像素，在一定的误差范围内，都落在指定区域的颜色统计范围之内。虽然用户交互很简单，但是找到正确的误差范围却非常的困难，甚至是不可能的。图(a)展示了使用Adobe Photoshop 7中Magic Wand方法的结果。由于前景和背景像素的颜色空间中的分布具有相当大的重叠，所以不能实现令人满意的分割。
Intelligent Scissors：允许用户通过用鼠标粗略追踪物体的边界来选择一个“最小成本轮廓”。如果所计算的轮廓不符合期望，那么就需要用户添加额外的seeds。图(b)展示了Adobe Photoshop 7中使用该方法的结果。
Bayes matting：基于颜色分布概率实现。将原图分为三部分(trimap)，即 $T=\lbrace T_B,T_U,T_F \rbrace$ 。其中， $T_B$ 是用户标记的背景区域， $T_F$ 是用户标记的前景区域， $T_U$ 是未被标记的区域。该方法通常可以获得比较好的抠图效果（见图©），但是前提条件是 $T_U$ 区域面积不是很大，并且前景和后景的颜色分布比较好区分。
Knockout 2：是Photoshop的专有插件，也需要用户定义trimap，类似于Bayes matting。二者的结果也是相似的。但是分割质量有时较低。结果见图(d)。
Graph Cut：请见本人的另一篇博客：【图像分割】Graph Cut算法，其分割效果见图(e)。（如果想深刻了解GrabCut算法，强烈推荐先学习Graph Cut算法。）

2.GrabCut图像分割算法

原论文地址：“GrabCut” — Interactive Foreground Extraction using Iterated Graph Cuts.

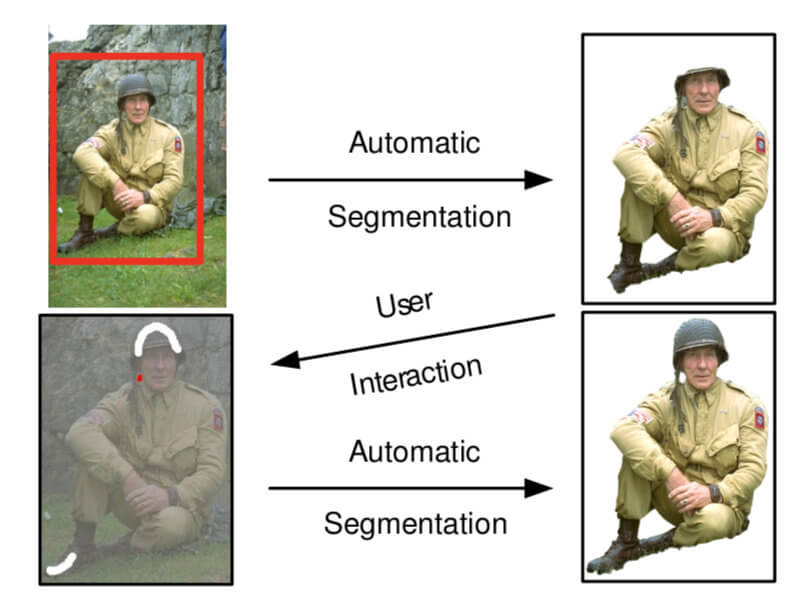
GrabCut图像分割算法是在Graph Cut算法的基础上，主要在三个方面进行了优化，最终减少了用户的交互式操作，改善了其分割结果，见图(f)。

接下来详细简介GrabCut都进行了哪三方面的优化。

2.1.彩色数据模型

GrabCut算法的惩罚函数的构造和Graph Cut类似：

也分为区域项和边界项：

区域项：
边界项：

（<…>表示求期望）

2.1.1.区域项

在Graph Cut中，区域项的计算是基于灰度直方图。对于彩色图像来说，这无疑会损失大量的信息，因此在GrabCut中，区域项采用高斯混合模型(Gaussian Mixture Model,GMM)。

高斯混合模型指的是多个高斯分布函数的线性组合，理论上GMM可以拟合出任意类型的分布。公式为：

$P(y\mid \theta)=\sum_{k=1}^K \alpha_k \phi(y\mid \theta_k)$

其中， $\alpha_k$ 是系数， $\alpha_k \geq 0$ , $\sum_{k=1}^K \alpha_k=1$ ； $\phi(y\mid \theta_k)$ 是高斯分布密度， $\theta_k=(\mu_k,\sigma_k^2)$ ，

$\phi(y\mid \theta_k)=\frac {1}{\sqrt{2\pi}\sigma_k}exp^{(-\frac{(y-\mu_k)^2}{2\sigma_k^2})}$

称为第 $k$ 个分模型，也称为第 $k$ 个分量。

但是需要注意的是，因为输入图像绝大部分都是RGB三通道的彩色图像，所以GMM中每个分模型都是三维高斯分布。多维高斯分布公式：

$N(\overline x \mid \overline \mu,\Sigma)=\frac {1}{(2\pi)^{\frac {D}{2}}} \frac{1}{\mid \Sigma \mid^{\frac{1}{2}}} exp[-\frac{1}{2}(\overline x- \overline \mu)^T\Sigma^{-1}(\overline x - \overline \mu)]$

其中， $\overline x$ 表示维度为 $D$ 的向量， $\overline \mu$ 则是这些向量的平均值， $\Sigma$ 表示所有向量 $\overline x$ 的协方差矩阵。

GrabCut算法中共构建两个GMM，一个用于前景，另一个用于背景。每个GMM均有五个高斯分量，即 $k = 5$ 。注意：为了方便计算能量函数最小化，2.1部分中的公式取了负对数。

2.1.2.边界项

边界项的公式基本和Graph Cut的一样，只是有稍微的变化：

对应Graph Cut论文，这里把 $R (A)$ 的系数 $\lambda$ 变更为 $\frac {1}{\lambda}$ 赋给 $B (A)$ 正比公式的后项（相当于式 $E(A)=\lambda R(A)+B(A)$ 两边同时除以 $\lambda$ ，因为 $\lambda \geq 0$ ，所以等式左边有没有 $\frac {1}{\lambda}$ 不影响求解最小值），再乘以一个常数 $p$ 使得正比关系变为相等关系，即有 $\gamma=\frac {p}{\lambda}$ 。