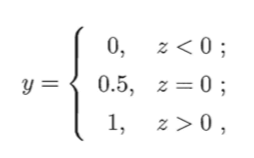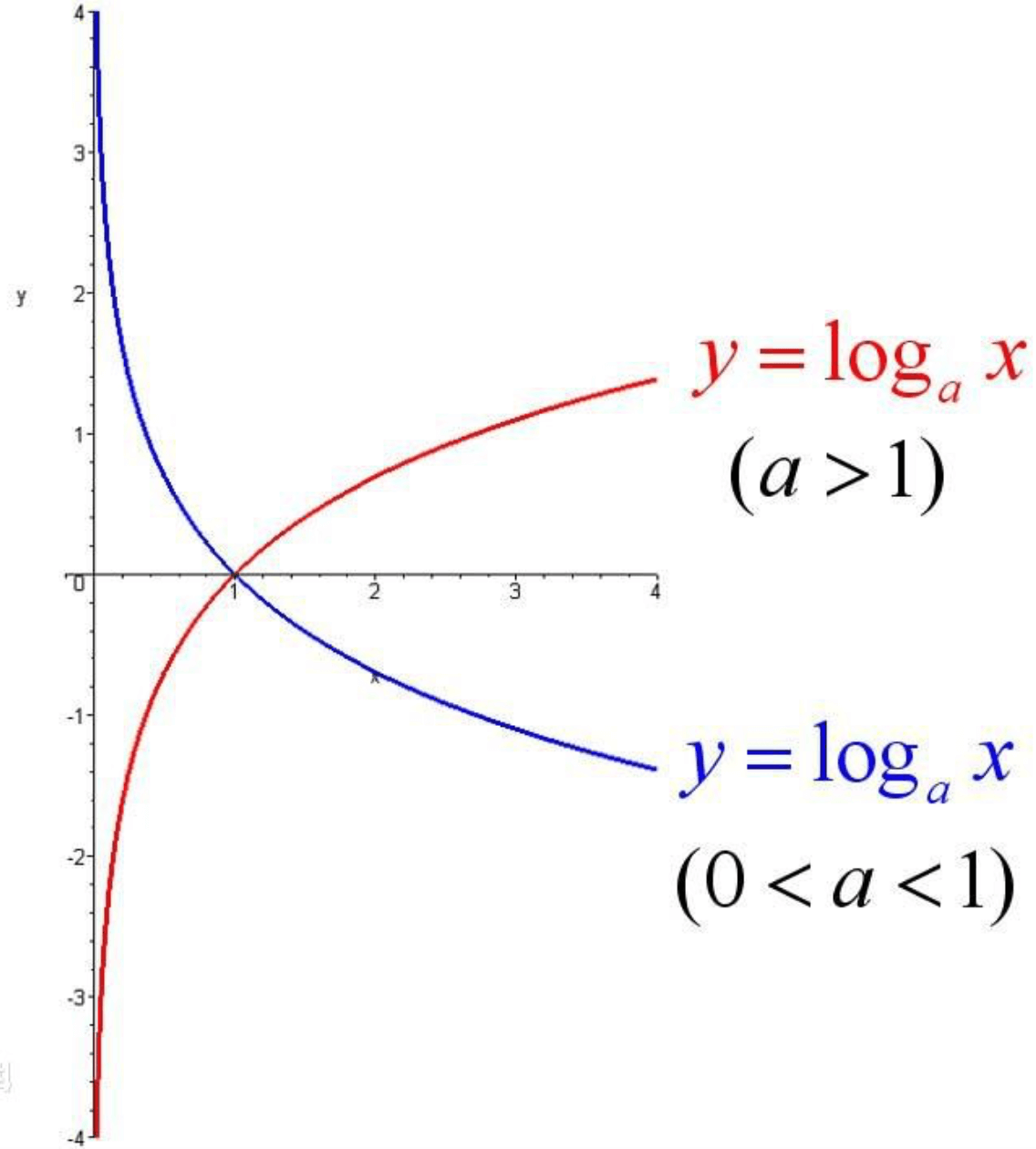【机器学习基础】系列博客为参考周志华老师的《机器学习》一书，自己所做的读书笔记。

1.对数几率回归

【机器学习基础】第六课中讨论了如何使用线性模型进行回归学习，但若要做的是分类任务该怎么办？答案就是广义线性模型。

考虑二分类任务，其输出标记 y ∈ { 0 , 1 } y \in \{0,1\} y∈{0,1}，而线性回归模型产生的预测值$z={\mathbf{w}}^T\mathbf{x}+b$是实值，于是，需将实值$z$转换成$0/1$值，最理想的是 “单位阶跃函数”(unit-step function)，亦称Heaviside函数：

即若预测值$z$大于零就判为正例，小于零则判为反例，预测值为临界值零则可任意判别：

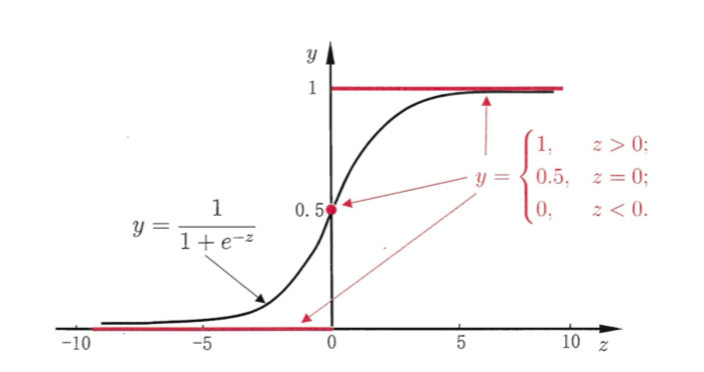
可以看出单位阶跃函数不连续，因此不能直接用作$g^{-}(\cdot )$，于是希望能在一定程度上近似单位阶跃函数“替代函数”，并希望它单调可微。对数几率函数(简称 “对率函数”，logistic function)(⚠️对率函数和对数函数不同)正是这样一个常用的替代函数：

$$y=\frac{1}{1+e^{-z}}\text{\hspace{1em}(1)}$$

从上图中可以看出，对率函数是一种 “sigmoid” 函数，并且其输出值在$z=0$附近变化很陡。

Sigmoid函数即形似S的函数，对率函数是Sigmoid函数最重要的代表。

将式（1）中的$z$代入：

$$y=\frac{1}{1+e^{-({\mathbf{w}}^T\mathbf{x}+b)}}\text{\hspace{1em}(2)}$$

式（2）可变为：

$$\ln \frac{y}{1-y}={\mathbf{w}}^T\mathbf{x}+b\text{\hspace{1em}(3)}$$

若将y视为样本$\mathbf{x}$作为正例的可能性，则1-y是其反例可能性，则两者的比值：

$$\frac{y}{1-y}$$

称为 “几率”（odds），反映了$\mathbf{x}$作为正例的相对可能性，对几率取对数则得到 “对数几率”（log odds，亦称logit） :

$$\ln \frac{y}{1-y}$$

上述模型就称为 “对数几率回归”（logistic regression，亦称logit regression）。

对数几率回归译成逻辑回归（logistic regression）其实并不恰当，因为和“逻辑”（logistic）一词并无关系。

对数几率回归名字中带有“回归”二字，但实际却是一种分类学习方法。

对率函数是任意阶可导的凸函数。

2.最大似然估计

简单来说，最大似然估计(Maximum likelihood estimation,MLE)就是:

利用已知的样本结果信息，反推最具有可能（最大概率）导致这些样本结果出现的模型参数值。

即给定数据集$\{({\mathbf{x}}_i,y_i){\}}_{i=1}^m$，推测哪一组参数$\theta$，可以使其等于真实标记$y_i$的概率最大。

3.对数几率回归的参数估计

将式（3）中的$y$视为条件概率：

$$\ln \frac{y}{1-y}=\ln \frac{p(y=1\mid \hat{\mathbf{x}};\beta )}{p(y=0\mid \hat{\mathbf{x}};\beta )}={\beta }^T\hat{\mathbf{x}}$$

其中$\beta =(\mathbf{w};b)，\hat{\mathbf{x}}=(\mathbf{x};1)$，则${\mathbf{w}}^T\mathbf{x}+b$可简写为${\beta }^T\hat{\mathbf{x}}$。（此处可参考【机器学习基础】第六课）。

很显然可计算得到：

$$y=p(y=1\mid \hat{\mathbf{x}};\beta )=\frac{e^{{\beta }^T\hat{\mathbf{x}}}}{1+e^{{\beta }^T\hat{\mathbf{x}}}}\text{\hspace{1em}(3.1)}$$

$$1-y=p(y=0\mid \hat{\mathbf{x}};\beta )=\frac{1}{1+e^{{\beta }^T\hat{\mathbf{x}}}}\text{\hspace{1em}(3.2)}$$

采用“极大似然法”来估计$\mathbf{w},b$。给定数据集$\{({\mathbf{x}}_i,y_i){\}}_{i=1}^m$，对率回归模型最大化 “对数似然”(log-likelihood)：

$$\ell (\mathbf{w},b)=\sum _{i=1}^m\ln p(y_i\mid \widehat{{\mathbf{x}}_i};\beta )\text{\hspace{1em}(3.3)}$$

连乘操作易造成下溢，所以通常使用对数似然（log-likelihood）。

式（3.3）中，只有$\beta$是未知的。即令每个样本属于其真实标记的概率越大越好。

对数函数图像：

对数计算法则：

1. ${\log }_a(MN)={\log }_{a}M+{\log }_{a}N$
2. ${\log }_a(\frac{M}{N})={\log }_{a}M-lo{g}_{a}N$
3. ${\log }_a{M}^n=n{\log }_{a}M$

令：

• $p_1(\hat{\mathbf{x}};\beta )=p(y=1\mid \hat{\mathbf{x}};\beta )$
• $p_0(\hat{\mathbf{x}};\beta )=p(y=0\mid \hat{\mathbf{x}};\beta )=1-p_1(\hat{\mathbf{x}};\beta )$

此时有：

$$p(y_i\mid \widehat{{\mathbf{x}}_i};\beta )=y_i{p}_1(\widehat{{\mathbf{x}}_i};\beta )+(1-y_i)p_0(\widehat{{\mathbf{x}}_i};\beta )\text{\hspace{1em}(3.4)}$$

当$y_i=1,p(y_i\mid \widehat{{\mathbf{x}}_i};\beta )=p_1(\widehat{{\mathbf{x}}_i};\beta )=\frac{e^{{\beta }^T\hat{\mathbf{x}}}}{1+e^{{\beta }^T\hat{\mathbf{x}}}}$

当$y_i=0,p(y_i\mid \widehat{{\mathbf{x}}_i};\beta )=p_0(\widehat{{\mathbf{x}}_i};\beta )=\frac{1}{1+e^{{\beta }^T\hat{\mathbf{x}}}}$

根据式(3.1),(3.2),(3.3),(3.4)可得：

• $$\ln p_1(\widehat{{\mathbf{x}}_i};\beta )={\beta }^T\widehat{{\mathbf{x}}_i}-\ln (1+e^{{\beta }^T\widehat{{\mathbf{x}}_i}})\text{\hspace{1em}(3.5)}$$
• $$\ln p_0(\widehat{{\mathbf{x}}_i};\beta )=-\ln (1+e^{{\beta }^T\widehat{{\mathbf{x}}_i}})\text{\hspace{1em}(3.6)}$$

把式(3.5),(3.6)代入式(3.4)并取自然对数（⚠️log运算不会影响函数本身的单调性，并且式子中有$e$，取自然对数可以减少计算量）：

$$\ln p(y_i\mid \widehat{{\mathbf{x}}_i};\beta )=y_i{\beta }^T\widehat{{\mathbf{x}}_i}-\ln (1+e^{{\beta }^T\widehat{{\mathbf{x}}_i}})\text{\hspace{1em}(3.7)}$$

$y_i=1$，式(3.7)变为式(3.5)

$y_i=0$，式(3.7)变为式(3.6)

此时我们需要求得式(3.7)的最大值，对式(3.7)进行取负，改为求最小值：

$$\ell (\beta )=\sum _{i=1}^m[-y_i{\beta }^T\widehat{{\mathbf{x}}_i}+\ln (1+e^{{\beta }^T\widehat{{\mathbf{x}}_i}})]\text{\hspace{1em}(3.8)}$$

这样做的原因是式(3.8)变为了高阶可导连续凸函数，这样就可以利用梯度下降法、牛顿法等求得最优解，于是就得到：

$${\beta }^{\ast }={\mathrm{argmin}}_{\beta }\ell (\beta )$$

以牛顿法为例，其第$t+1$轮迭代解的更新公式为：

$${\beta }^{t+1}={\beta }^t-(\frac{{\partial }^2\ell (\beta )}{\partial \beta \partial {\beta }^T}{)}^{-1}\frac{\partial \ell (\beta )}{\partial \beta }$$

代入$\beta$的一阶导和二阶导即可。

想要获取最新文章推送或者私聊谈人生，请关注我的个人微信公众号：⬇️x-jeff的AI工坊⬇️

个人博客网站：https://shichaoxin.com

GitHub：https://github.com/x-jeff