数据结构与算法（C语言） | 排序算法

　排序是计算机内经常进行的一种操作，其目的是将一组“无序”的记录序列调整为“有序”的记录序列。

——–假设含有n个记录的序列为{r1,r2,…,rn}，其相应的关键字分别为{k1,k2,…,kn}，需确定1,2,…,n的一种排列p1,p2,…pn,使其相应的关键字满足kp1<=kp2<=…<=kpn非递减（或非递增）关系，即使得序列成为一个按关键字有序的序列{rp1,rp2,…rpn}，这样的操作就称为排序。

•在排序问题中，通常将数据元素称为记录。

–显然我们输入的是一个记录集合，排序后输出的也是一个记录集合。

–所以我们可以将排序看成是线性表的一种操作。

•排序的依据是关键字之间的大小关系，那么对同一记录集合，针对不同的关键字进行排序，可以得到不同序列。

内部排序和外部排序——

若待排序记录可全部放入内存，整个排序过程不需要访问外存便能完成，则称此类排序问题为内部排序；　　

若待排序记录的数量很大，以至内存一次不能容纳全部记录，在排序过程中尚需对外存进行访问，则称此类排序问题为外部排序。

排序方法的稳定性——

对于一种排序方法，若排序后具有相同关键字的记录仍维持原来的相对次序，则称之为稳定的，否则称之为不稳定的。　　

影响排序算法性能的几个要素——时间性能、辅助空间、算法的复杂性

冒泡排序（通过频繁的交换完成排序）：

1.两两注意是相邻的两个元素的意思

2.如果有n个元素需要比较n-1次，每一轮减少1次比较

3.既然叫冒泡排序，那就是从下往上两两比较，所以看上去就跟泡泡往上冒一样。

#include<stdio.h>
void BubbleSort(int k[], int n)
{
    int i, j, temp, count1=0, count2=0;
    for(i=0 ;i<n-1 ;i++)
    {
        for(j=n-1 ;j > i ;j--)
        {
            count1++;
            if(k[j-1] > k[j])
            {
                count2++;
                temp = k[j-1];
                k[j-1]= k[j];
                k[j] = temp;

            }
        }
    }
    printf("总共进行了%d次比较，进行了%d次移动！", count1, count2);

}
int main()
{
    int i ,a[10] ={11,2,6,4,22,31,0,9,7,13};
    BubbleSort(a, 10);
    printf("排序后的结果是：");
    for(i =0;i<10 ;i++)
    {
        printf("%d ",a[i]);
    }
    return 0;
}

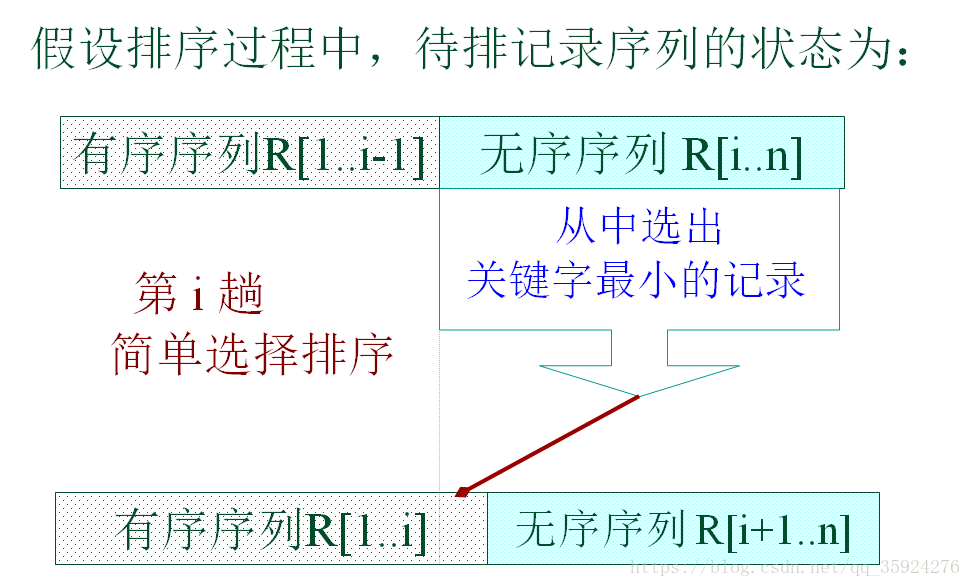
选择排序：

选择排序法是对定位比较交换法（也就是冒泡排序法）的一种改进。选择排序的基本思想是：每一趟在n-i+1（i=1，2，…n-1）个记录中选取关键字最小的记录作为有序序列中第i个记录。

简单选择排序：

#include<stdio.h>
void SlecetSort(int k[], int n)
{
    int i, j, temp, count1=0, count2=0;;
    for(i=0 ;i< n-1; i++)
    {
        int min = i;
        for(j =i+1;j<n ;j++)
        {
            count1++;
            if(k[j]<k[min])
            {
                min = j;
            }
        }
        if(min !=i)
        {
            count2++;
            temp = k[min];
            k[min] = k[i];
            k[i] = temp;
        }
    }
    printf("总共进行了%d次比较，进行了%d次移动！", count1, count2);
}
int main()
{
    int i ,a[10] ={11,2,6,4,22,31,0,9,7,13};
    SlecetSort(a, 10);
    printf("排序后的结果是：");
    for(i =0;i<10 ;i++)
    {
        printf("%d ",a[i]);
    }
    return 0;
}

直接插入排序（最简单，基于顺序查找）：

void InsertSort(int k[],int n)
{
    int i, j, temp;
    for(i=1; i<n ;i++)
    {
        if(k[i]<k[i-1])
        {
            temp = k[i];
            for(j =i-1; k[j] > temp;j--)
            {
                k[j+1] = k[j];
            }
            k[j+1] = temp;
        }
    }
}

希尔排序（缩小增量排序）：

将记录序列分成若干子序列（逻辑上分组），分别对每个子序列进行插入排序。此时插入排序所作用的数据量比较小（每一个小组），插入的效率比较高

例如：将 n 个记录分成 d 个子序列：

{ R[1]，R[1+d]，R[1+2d]，…，R[1+kd] }

{ R[2]，R[2+d]，R[2+2d]，…，R[2+kd] }

…

{ R[d]，R[2d]，R[3d]，…，R[kd]，R[(k+1)d] }

其中，d 称为增量，它的值在排序过程中从大到小逐渐缩小，直至最后一趟排序减为 1。

就像直接插入排序跨度为1

实现分组有序整体不一定有序

void ShellSort(int k[], int n)
{        
    int i,j,temp;
    int dk;
     //进行分组，最开始的增量为数组长度的一半
    for(dk = n/2; dk>0 ; dk /=2)
    {

    	//对数组做一趟希尔插入排序，dk为本趟增量
	for( i=dk; i < n; i++ )//分别向每组的有序区域插入
	{
	    if( k[i] < k[i-dk] )
	    {
	        temp = k[i];
	
        	for( j=i-dk; k[j] > temp; j-=dk )//比较与记录后移同时进行
	        {
	            k[j+dk] = k[j];
	        }
	
	        k[j+dk] = temp;
	    }
	} 
    }


}

希尔排序不是稳定的，虽然插入排序是稳定的，但是希尔排序在插入的时候是跳跃性插入的，有可能破坏稳定性

堆排序：

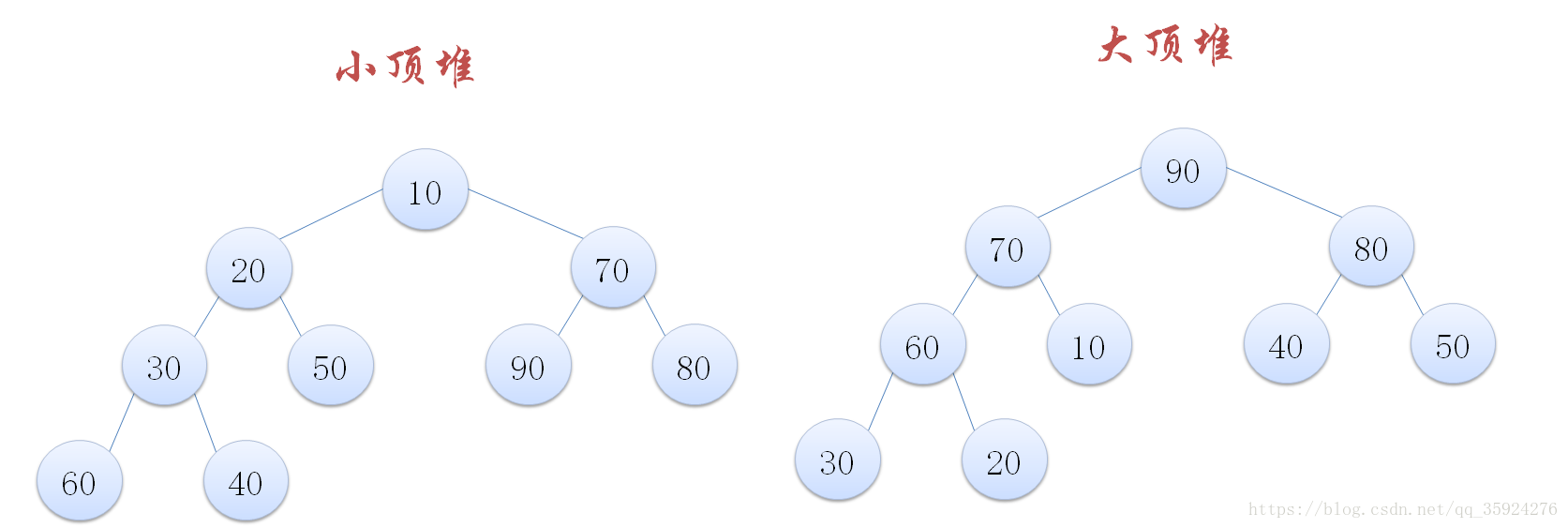
堆是 n 个元素的序列 ( K1, K2, …,Kn )，该序列满足如下条件：

在完全二叉树中根结点一定是堆中所有结点最大或者最小者

下标i与2i和2i+1是双亲和子女关系。

那么把大顶堆和小顶堆用层序遍历存入数组，则一定满足上面的表达式。

堆排序算法

•堆排序（Heap Sort）就是利用堆进行排序的算法，它的基本思想是：

–将待排序的序列构造成一个大顶堆（或小顶堆）。

–此时，整个序列的最大值就是堆顶的根结点。将它移走（就是将其与堆数组的末尾元素交换，此时末尾元素就是最大值）。

–然后将剩余的n-1个序列重新构造成一个堆，这样就会得到n个元素中的此大值。

–如此反复执行，便能得到一个有序序列了。


void swap(int k[], int i, int j)
{
	int temp;

	temp = k[i];
	k[i] = k[j];
	k[j] = temp;
}

void HeapAdjust(int k[], int s, int n)
{
	int i, temp;

	temp = k[s];

	for( i=2*s; i <= n; i*=2 )
	{
		if( i < n && k[i] < k[i+1] )
		{
			i++;
		}

		if( temp >= k[i] )
		{
			break;
		}

		k[s] = k[i];
		s = i;
	}

	k[s] = temp;
}

void HeapSort(int k[], int n)
{
	int i;

	for( i=n/2; i > 0; i-- )
	{
		HeapAdjust(k, i, n);
	}

	for( i=n; i > 1; i-- )
	{
		swap(k, 1, i);
		HeapAdjust(k, 1, i-1);
	}
}

归并排序：

归并排序的基本思想——

假设初始序列含有 n 个记录，则可看成是 n 个有序的子序列，每个子序列的长度为1，然后两两归并，得到 én/2ù 个长度为 2 或 1 的有序子序列；再两两归并，……，如此重复，直至得到一个长度为 n 的有序序列为止，这种排序方法称为2-路归并排序。

　2-路归并排序的核心操作：将两个位置相邻的记录有序子序列，归并为一个记录的有序序列。

　容易看出，对 n 个记录进行归并排序的时间复杂度为Ο(n·log2n)。即：

每一趟归并的时间复杂度为 O(n)，

总共需进行 élog2nù 趟。

　归并排序需要和待排记录等数量的辅助空间，即空间复杂度为O(n)。归并排序是需要辅助空间最多的一种排序方法。

#include<stdio.h>
#define     MAXSIZE 20
//递归实现归并，并把最后的结果存放到list1
void merging(int *list1,int list1_size,int *list2, int list2_size)
{
    int i, j, k;
    int temp[MAXSIZE];

    i = j = k = 0;
    while(i < list1_size && j<list2_size)
    {
        if(list1[i] < list2[j])
        {
            temp[k++] = list1[i++];
        }
        else
        {
            temp[k++] = list2[j++];
        }
    }
    while(i < list1_size)
    {
        temp[k++] = list1[i++];
    }
    while(j < list2_size)
    {
        temp[k++] = list2[j++];
    }

    int m;
    for(m=0; m < list1_size+list2_size; m++)
    {
        list1[m] = temp[m];
    }
}
void mergeSort(int k[],int n)
{
    if(n>1)
    {
        int *list1 = k;
        int list1_size = n/2;
        int *list2 = k + n/2;
        int list2_size = n - list1_size;

        mergeSort(list1, list1_size);
        mergeSort(list2, list2_size );

        merging(list1, list1_size,list2, list2_size);
    }

}

int main()
{
	int i, a[10] = {5, 2, 6, 0, 3, 9, 1, 7, 4, 8};

	mergeSort(a, 10);

	printf("排序后的结果是：");
	for( i=0; i < 10; i++ )
	{
		printf("%d ", a[i]);
	}
	printf("\n\n");

	return 0;
}

//迭代实现
void MergeSort(int k[], int n)
{
	int i, next, left_min, left_max, right_min, right_max;
	int *temp = (int *)malloc(n * sizeof(int));

	for( i=1; i < n; i*=2 ) 
	{
		for( left_min=0; left_min < n-i; left_min = right_max )
		{
			right_min = left_max = left_min + i;
			right_max = left_max + i;

			if( right_max > n )
			{
				right_max = n;
			}

			next = 0;

			while( left_min < left_max && right_min < right_max )
			{
				if( k[left_min] < k[right_min] )
				{
					temp[next++] = k[left_min++];
				}
				else
				{
					temp[next++] = k[right_min++];
				}
			}

			while( left_min < left_max )
			{
				k[--right_min] = k[--left_max];
			}

			while( next > 0 )
			{
				k[--right_min] = temp[--next];
			}
		}
	}
}

快速排序

快速排序(Quick Sort)使用分治法策略。它的基本思想是：选择一个基准数，通过一趟排序将要排序的数据分割成独立的两部分；其中一部分的所有数据都比另外一部分的所有数据都要小。然后，再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

流程如下：

从数列中挑出一个基准值。
将所有比基准值小的摆放在基准前面，所有比基准值大的摆在基准的后面(相同的数可以到任一边)；在这个分区退出之后，该基准就处于数列的中间位置。
递归地把"基准值前面的子数列"和"基准值后面的子数列"进行排序。

void quickSort(int a[], int l, int r)
{
    if( l<r )
    {
        int i,j,x;
        i=l;
        j=r;
        x = a[i];
        while(i<j)
        {
            while(x<a[j] && i<j)   
                j--;// 从右向左找第一个小于x的数
            if(i<j)
                a[i++] = a[j];
            while(x>a[i] && i<j)   
                i++;// 从左向右找第一个大于x的数
            if(i<j)
                a[j--] = a[i];
        }
        a[i] = x;
        quickSort(a,l,i-1);
        quickSort(a,i+1,r);
    }

}

快速排序性能分析：

快速排序的稳定性：快速排序是不稳定的算法，它不满足稳定算法的定义；所谓算法稳定性指的是对于一个数列中的两个相等的数a[i]=a[j]，在排序前,a[i]在a[j]前面，经过排序后a[i]仍然在a[j]前，那么这个排序算法是稳定的。

	排序方法	最好情况	最坏情况	平均时间	辅助存储	稳定性
1	直接插入	O(n)	O(n2)	O(n2)	O(1)	稳定
2	折半插入	O(n)	O(n2)	O(n2)	O(1)	稳定
3	希尔排序	——	——	——	O(1)	不稳定
4	起泡排序	O(n)	O(n2)	O(n2)	O(1)	稳定
5	快速排序	O(nlog2n)	O(n2)	O(nlog2n)	O(log2n)	不稳定
6	简单选择	O(n2)	O(n2)	O(n2)	O(1)	不稳定
7	堆排序	O(nlog2n)	O(nlog2n)	O(nlog2n)	O(1)	不稳定
8	归并排序	O(nlog2n)	O(nlog2n)	O(nlog2n)	O(n)	稳定
9	基数排序	O(d(n+rd))	O(d(n+rd))	O(d(n+rd))	O(n+rd)	稳定