正向运动学指的是通过相邻关节间的转动和移动坐标,将末端的坐标计算出来。
反向运动学指的是已知机械臂末端的坐标,反算每个关节可能的转动和移动参数。
参考资料:4.机械臂几何法与DH表示法_哔哩哔哩_bilibili
一.任意连杆连接的变量定义(Craig DH)
假设对于任意轴,只存在转动或移动。
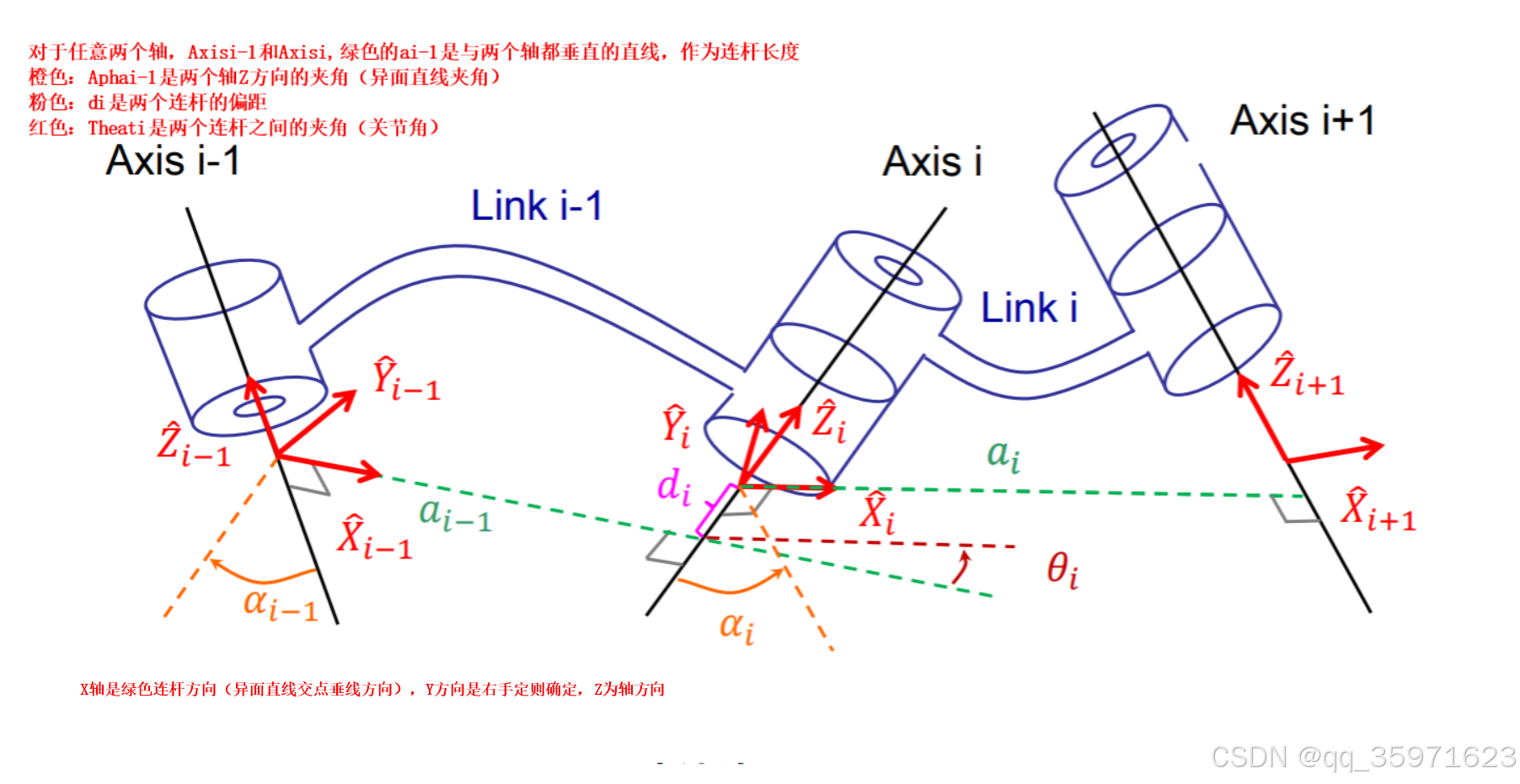
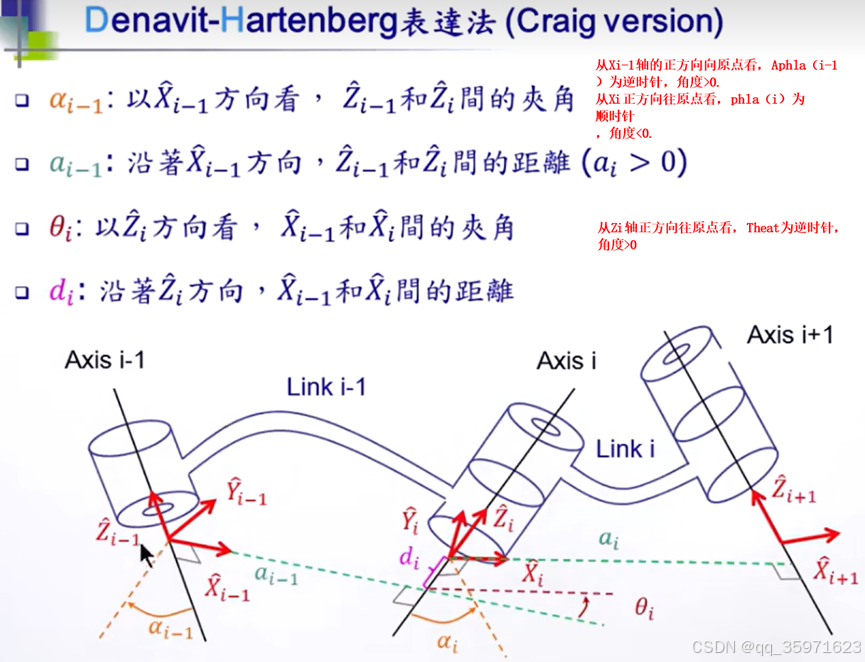
对于任意多个轴连接,相邻两个轴之间,其连杆(绿色),轴的夹角(橙色),连杆的偏距(紫色),关节角(红色)如下图所示。
其方向为X轴沿着连杆方向,Y轴为右手定则方向,Z轴为旋转方向右手定则指向的大拇指方向
多杆连接时,一共有四个参数(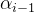
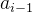


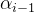
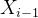
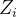
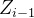
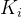
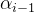
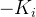
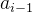
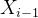
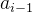

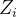


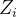
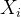
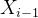
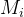

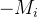
二.不同坐标系间的坐标变换
对于两个坐标系间的坐标变换,存在:点Pa为A系下的坐标,若要变成B系,则=R
+
=
,其中
为A系到B系的变换矩阵;相当于A系在B系中的位姿坐标;相当于B系经过平移旋转和A系重合时,该平移旋转的组成为变换矩阵
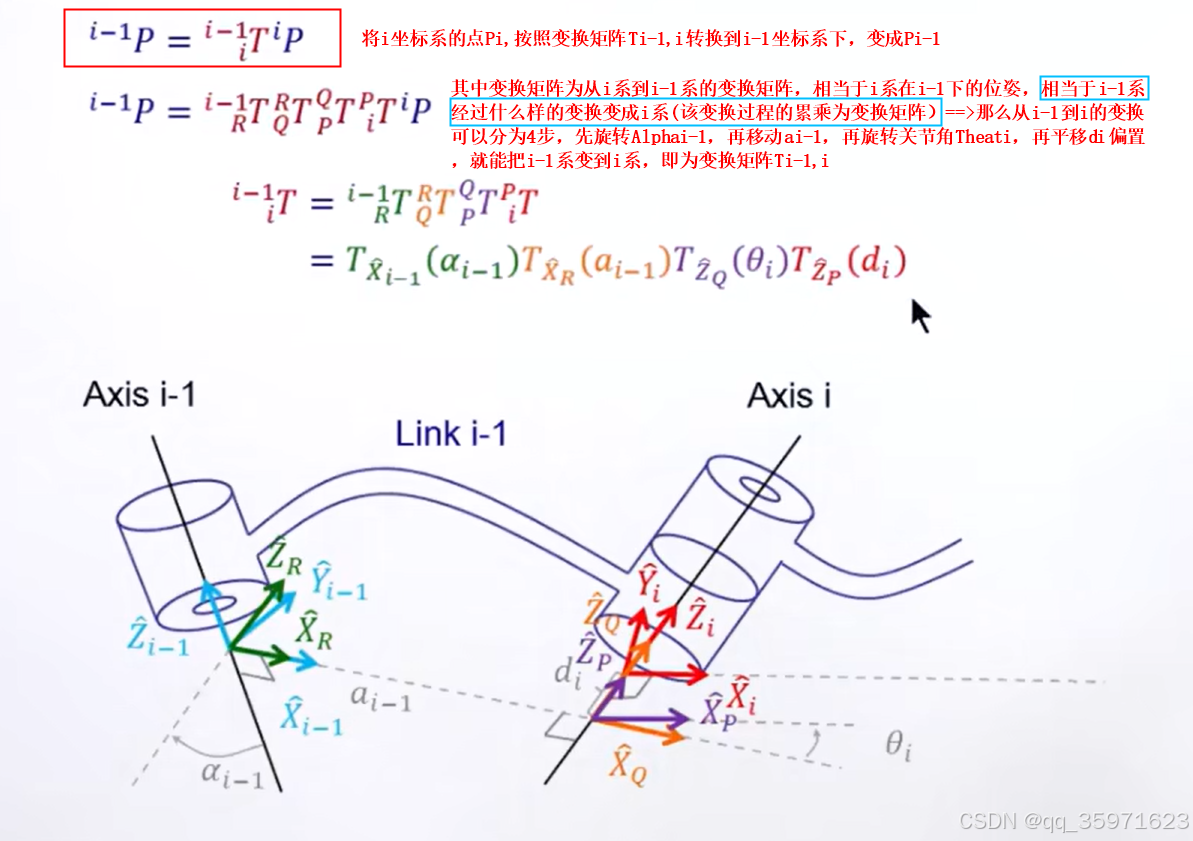
那么对于两个轴之间的坐标转换,若要将第i个坐标系的点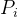
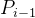
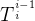
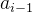
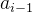
3)将Q坐标系经过
4)将P坐标系经过
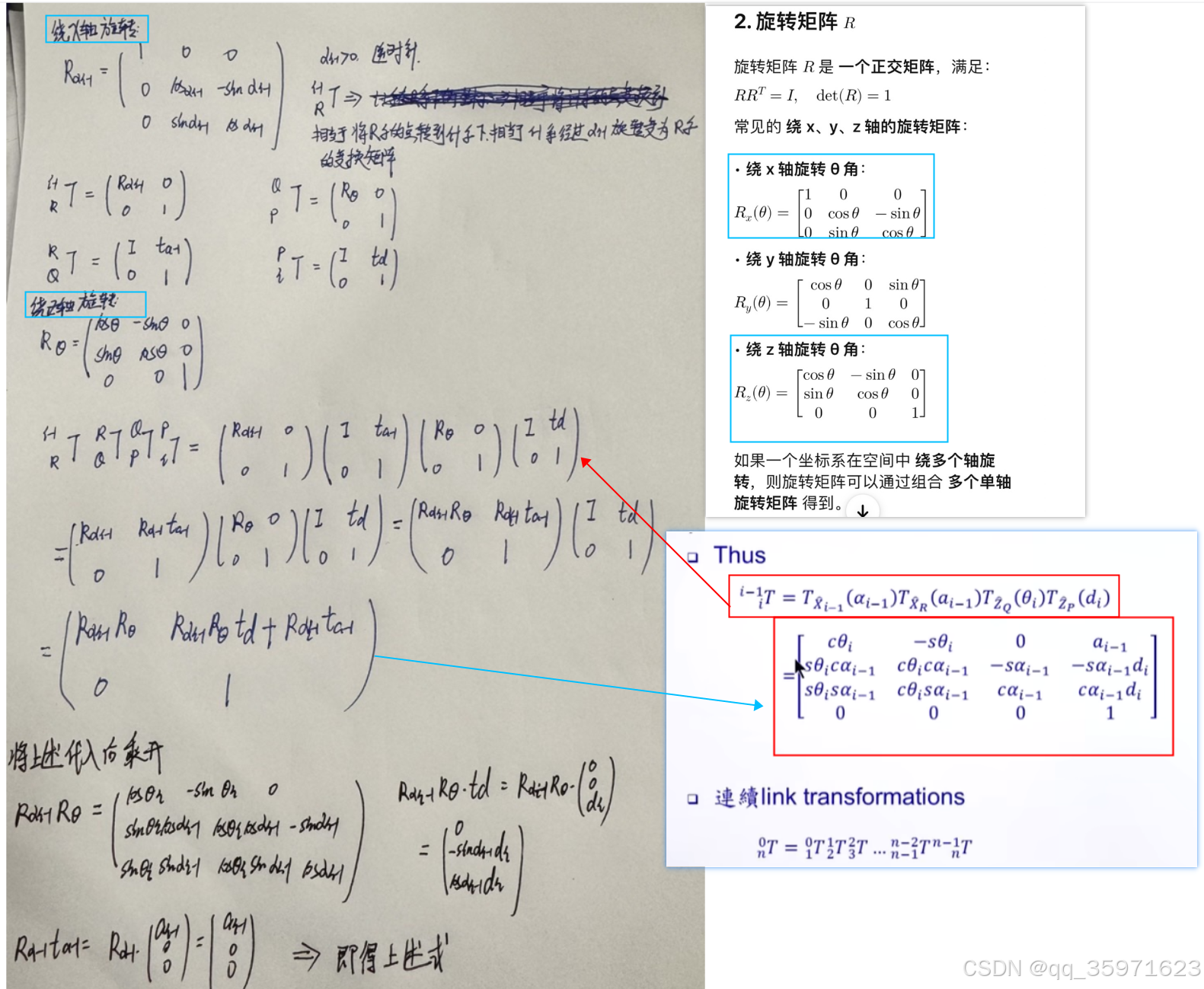
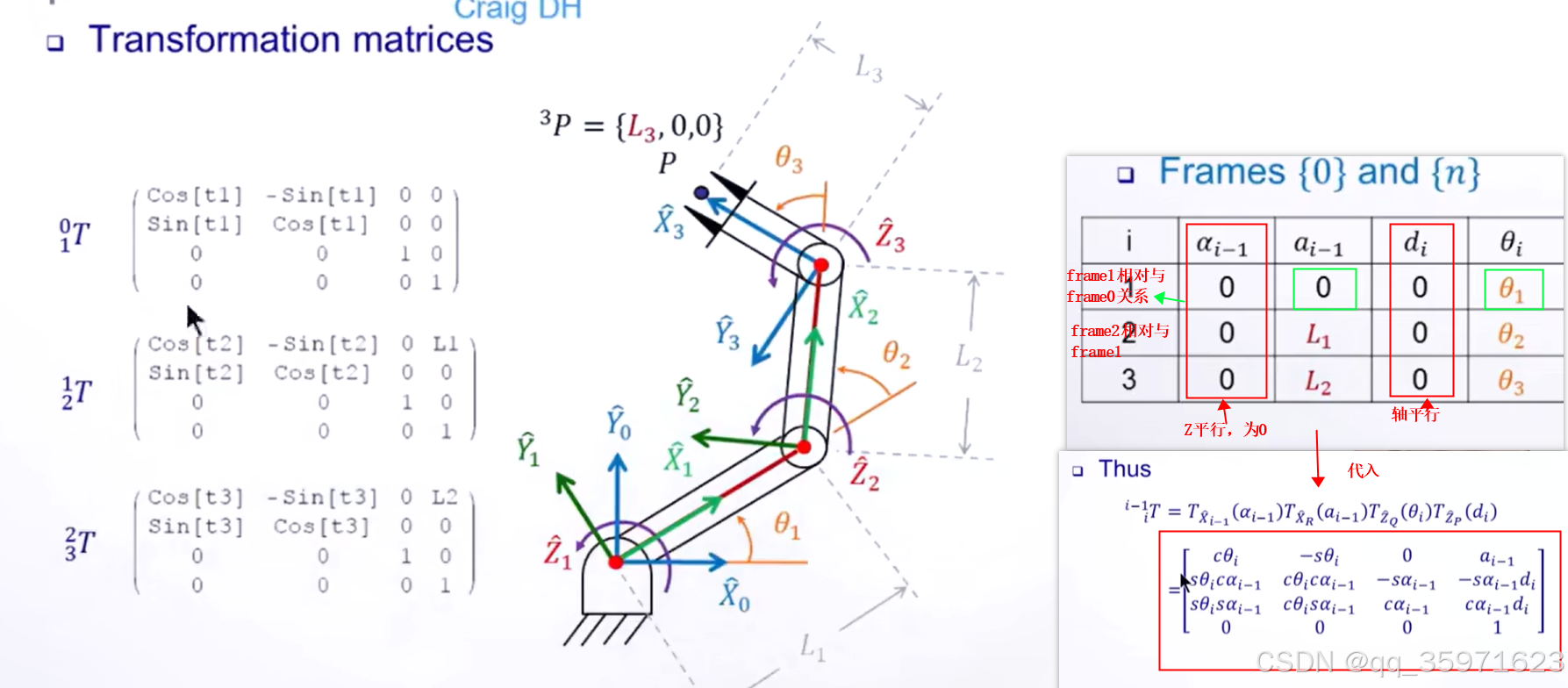
三.通用的变换矩阵计算
按照上述的变换方式,计算变换矩阵如下:
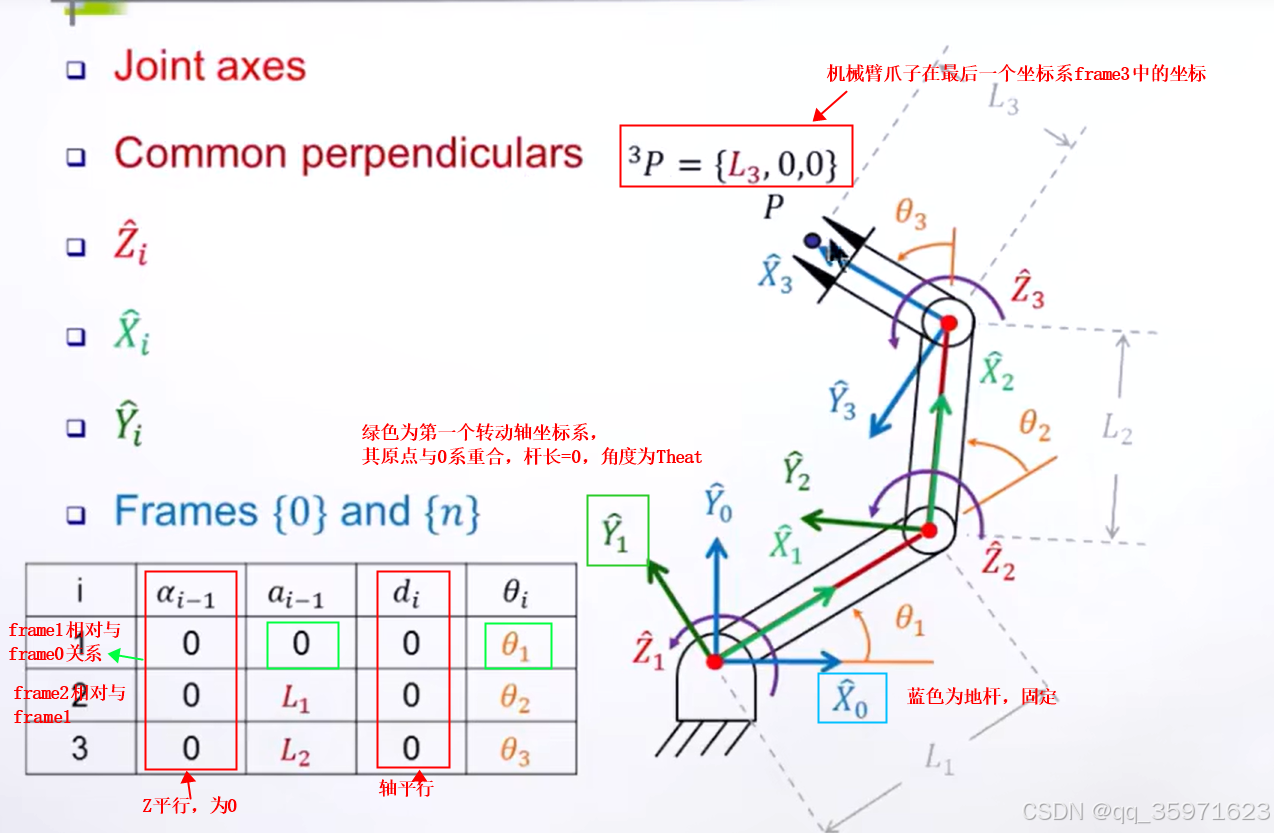
四:例1:对于RRR(3转轴)平面机械臂
平面机械臂:其Z轴互相平行,则所有的Z轴夹角=0;其连杆都在同一平面上,连杆的偏距
=0;
地杆frame0坐标系不动(可理解为基座标),其坐标原点与第一个杆坐标系重合,沿着X0方向,两个坐标系的位移为0,故=0,转角
=
机械臂末端(爪子),相对于最后一个坐标系frame3的坐标为(L3,0,0)
将上述的四个参数代入通用表达式,可以得到对应的变换矩阵。
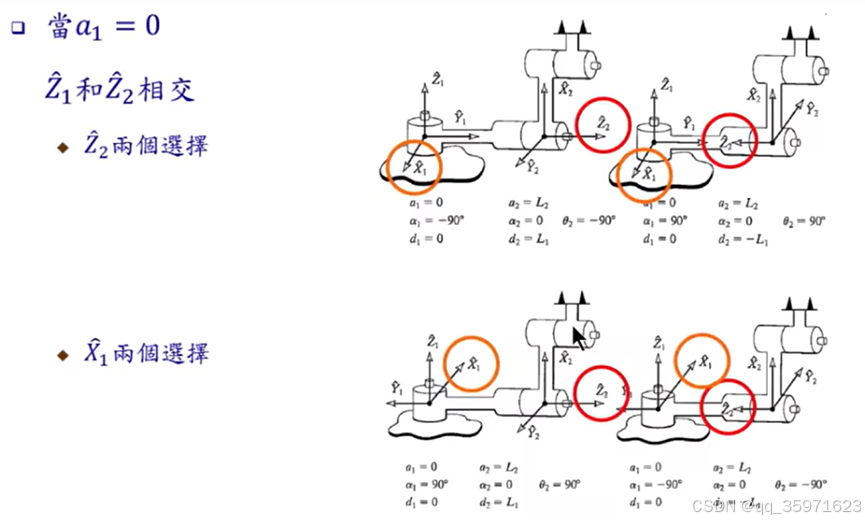
五.例2:RRR非平面三转轴机械臂
其Z轴和X轴各有两种选择方案,共有四种选择方案
以第一种为例:
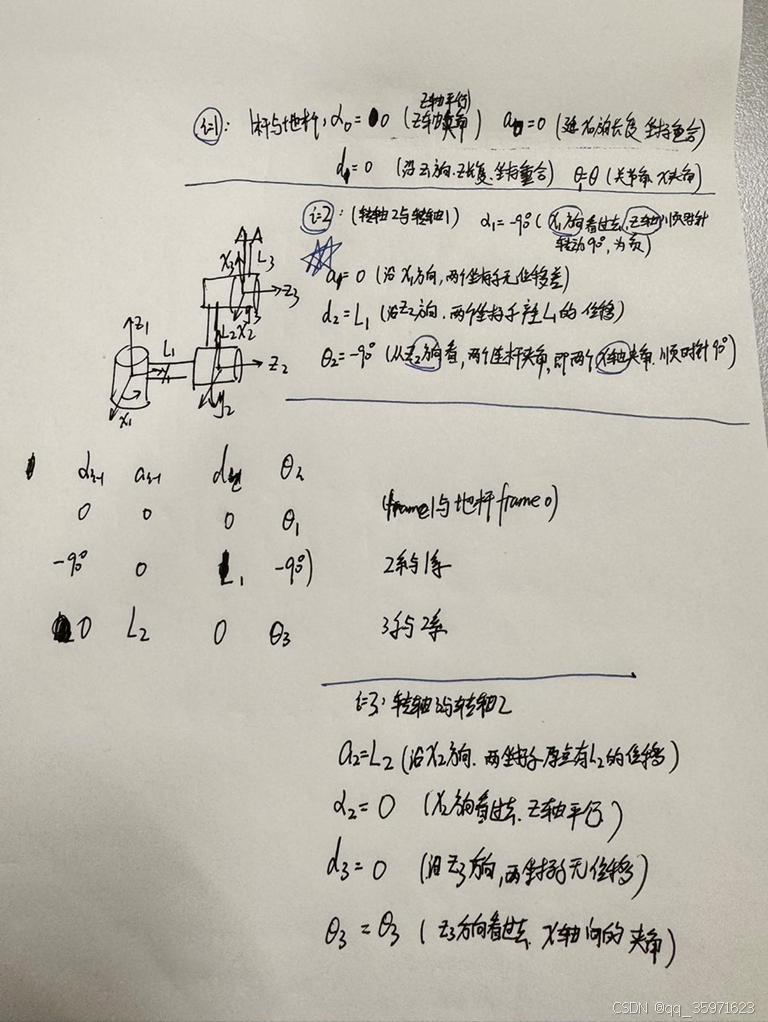
图中,以i=2为例,即2轴与1轴的坐标系转换关系
:从第frame_1坐标系的X1向其坐标系原点看过去,Z2相对于Z1的旋转角度为顺时针90度,则
=-90
:沿着第frame_1坐标系的X1方向,两个坐标系原点未发生位移,则
=0
:沿着第frame_2坐标系的Z2方向,两个坐标系的原点发生了L1的位移,则
=L1
:从第frame_2坐标系的Z2向其坐标原点看过去,X2轴相较于X1轴顺时针旋转90度,