动态时间规整算法(Dynamic Time Warping )
来源:
-假定一个孤立词识别系统,利用模板匹配法进行识别。训练阶段,用户将词汇表种每一个词都念一遍,将其特征矢量的时间序列作为模板(template)存入模板库;识别阶段,将输入语音的特征矢量时间序列与模板库中的每个模板进行相似度比较,将相似度最高的最为识别输出。
-实际上,这样做识别率很低,因为语音信号随机性太强了,同一个人在不同时刻讲同一句话,发同一个音,也不可能具有完全相同的时间长度。
-对此,日本学者板仓(Itakura)将动态规划算法(DP)应用于解决说话速度步不均匀的难题,提出DTW算法。
DTW算法:
按照距离最近原则,衡量两个长度不同的时间序列的相似度的方法,是一种非线性规整技术。
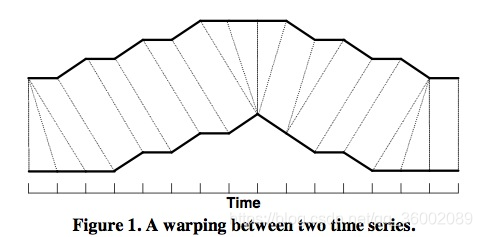
如下图所示,上下两条实线代表两个时间序列,时间序列之间的虚线代表两个时间序列之间的相似的点。DTW使用所有这些相似点之间的距离的和,称之为归整路径距离(Warp Path Distance)来衡量两个时间序列之间的相似性。
- 要求:
1.单向对应,不能回头,从前往后对齐。
2.一一对应,中间不能有空元素。
3.对应之后,距离最近。
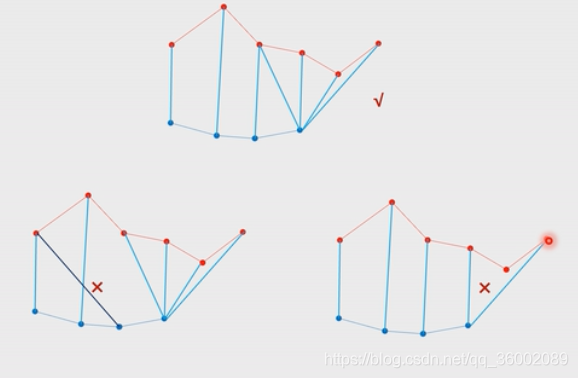
如下图所示,第一个是对的,下面两个都是错的。下左是因为回头了,导致有交叉,所以不对;下右是有空缺。
下面根据一个具体例子:
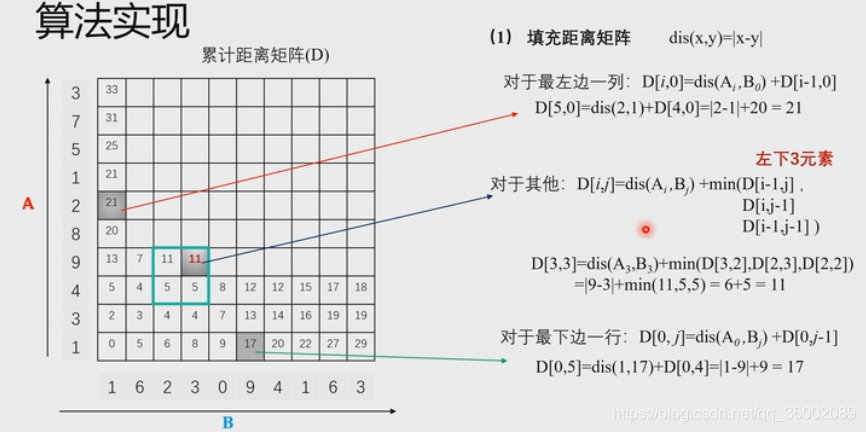
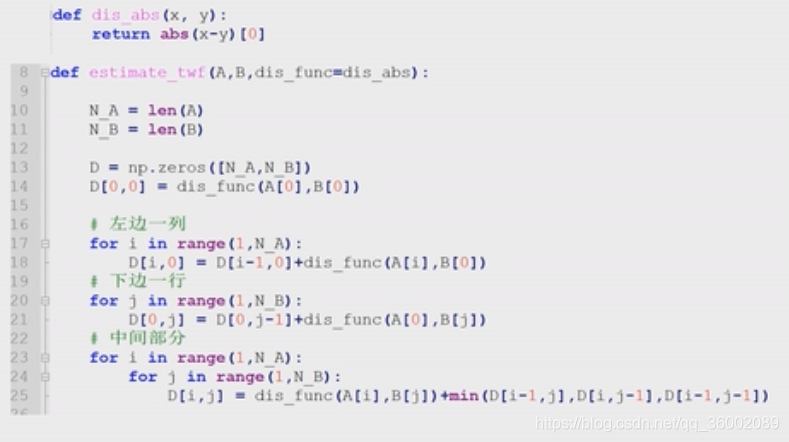
有A和B两个序列,都是一维特征,长度10。图上两条数是特征值。当然也可以是不同长度的序列。若A长m,B长n,就得到m*n的矩阵。矩阵从(0,0)开始。此处用最简单的欧氏距离衡量dis=|x-y|。该矩阵叫累计距离矩阵。,因为其计算D[i,j]的值是前当前计算值dis(Ai,Bj)加上上一步的最小值,这样相当于每步都在不断累计。
分三种情况,左边第一列,下面第一行,和其他。
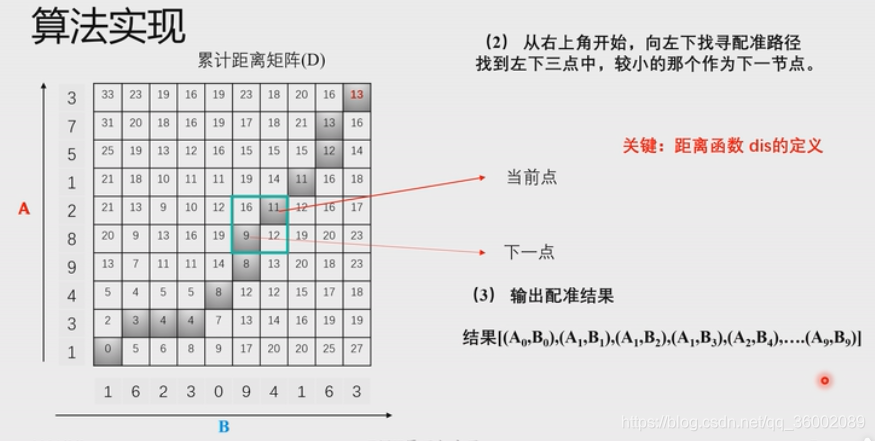
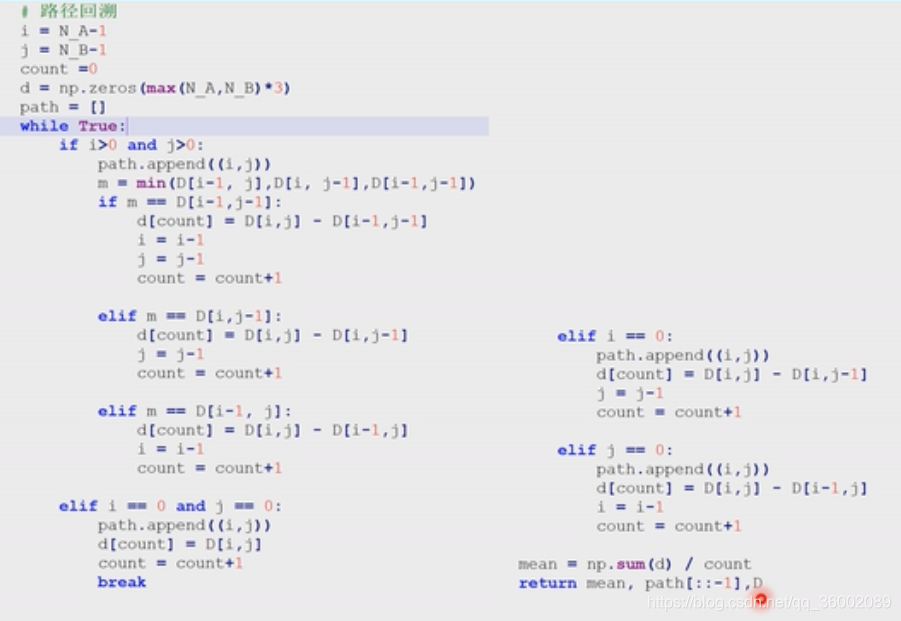
最后将整个网络计算完填满,根据最小距离原则找对A和B的对应关系,找到一条最优路径,起点必须(0,0),终点必须(m-1,n-1)。从右上方开始,在左下方的三个点里找最小的一个点,最后反转一下。
python代码实现:
输入A,B序列,存放格式:[N样本数目,D特征维度]。
count;统计最终得到多少个配对点。
d:记录配对点的距离。
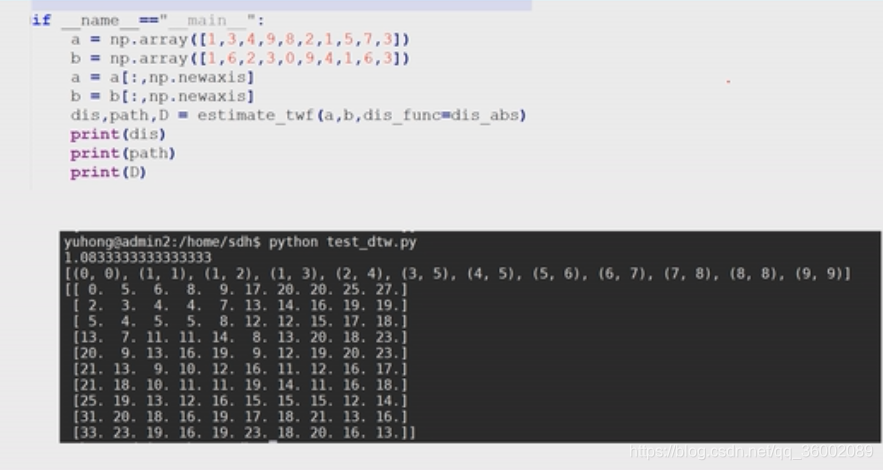
结果:
上面代码比较繁琐,目前有现成的DTW工具,简便参数易修改。
现成的DTW的python包:
- pip install dtw
- pip install dtw_c
- pip install fastdtw
如何调用实现,参考例子:https://www.cnblogs.com/HoEn/
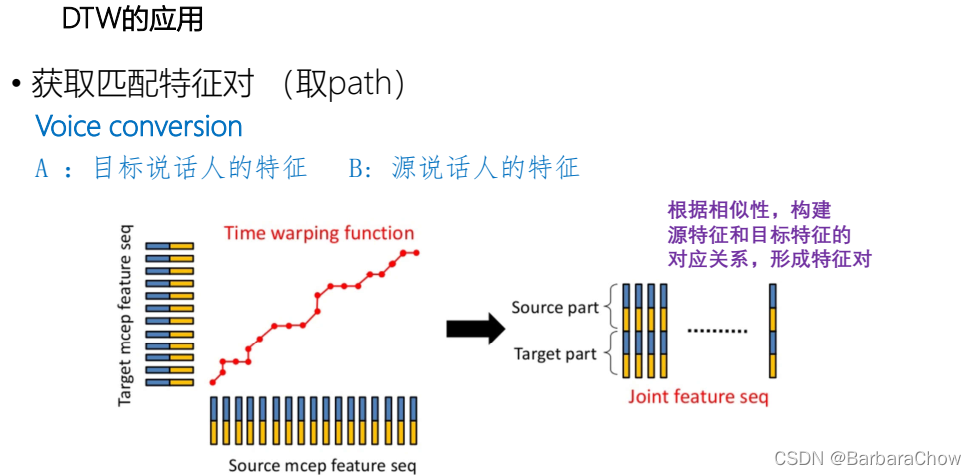
应用