随着无人机、机器人和自动驾驶技术的快速发展,三维路径规划成为一个备受关注的研究领域。如何在复杂的环境中找到一条高效、平滑并避开障碍物的路径,是许多工程师和科学家面临的挑战。
在这篇博客中,我们深入探讨了一种基于 Python 的三维路径规划框架。通过对 UAV_DPPA_DWA、MASAC 和 AHPP 等三种经典路径规划算法的比较,我们展示了不同算法在复杂环境下的表现,并从路径长度、碰撞次数、飞行时间等维度进行了全面的评估。
一、路径规划的背景与意义
三维路径规划的核心目标是找到一条从起点到目标点的最优路径,同时避开环境中的障碍物。算法不仅需要考虑效率,还需兼顾平滑性和安全性。在实际应用中,这些算法广泛应用于:
- 无人机的智能巡航
- 机器人在仓储中的路径优化
- 自动驾驶汽车在复杂城市环境中的决策
二、路径规划算法的实现
本次实验实现了三个核心算法,每个算法各具特色:
1. UAV_DPPA_DWA - 短期动态窗口避障
该算法基于动态窗口法 (Dynamic Window Approach),结合了方向选择与局部避障的策略。它快速评估路径的安全性,并以最小的计算开销生成下一步运动方向。
direction = (goal - current) / np.linalg.norm(goal - current)
next_pos = current + direction * min(5, np.linalg.norm(goal - current))
优点:
- 简单高效,适合实时系统
- 在低密度障碍物环境中表现良好
缺点:
- 对复杂障碍物布局的全局规划能力有限
2. MASAC - 动态加速度控制的平滑路径
MASAC 通过引入动态加速度限制,确保路径平滑且控制合理。它模拟了车辆的运动学模型,在速度与路径优化之间取得平衡。
desired_vel = (goal - current) * 2
acc = np.clip(desired_vel - velocity, -max_acc, max_acc)
优点:
- 路径平滑,转向角度小
- 在连续障碍物环境中表现较好
缺点:
- 计算开销略高
3. AHPP - 自适应启发式路径规划
AHPP 是一种高级算法,结合了多种路径优化技术,包括初始路径优化、RRT* 搜索、平滑处理和后处理,旨在生成全局最优路径。
核心流程:
- 初始路径优化:从多个初始路径中选择成本最低的路径
- RRT* 搜索:结合启发式采样生成新路径
- 平滑与后处理:确保路径的平滑性和可用性
tck, u = splprep(path.T, s=0, k=3) u_new = np.linspace(0, 1, 1000) smooth = np.column_stack(splev(u_new, tck))三、性能对比:真实场景测试
我们设计了三个不同的测试场景,环境大小为 200×200×200,包含 20 个随机生成的椭球形障碍物。
测试场景描述
- 场景 1:从 (0, 0, 0) 到 (200, 200, 200),典型的对角线规划问题。
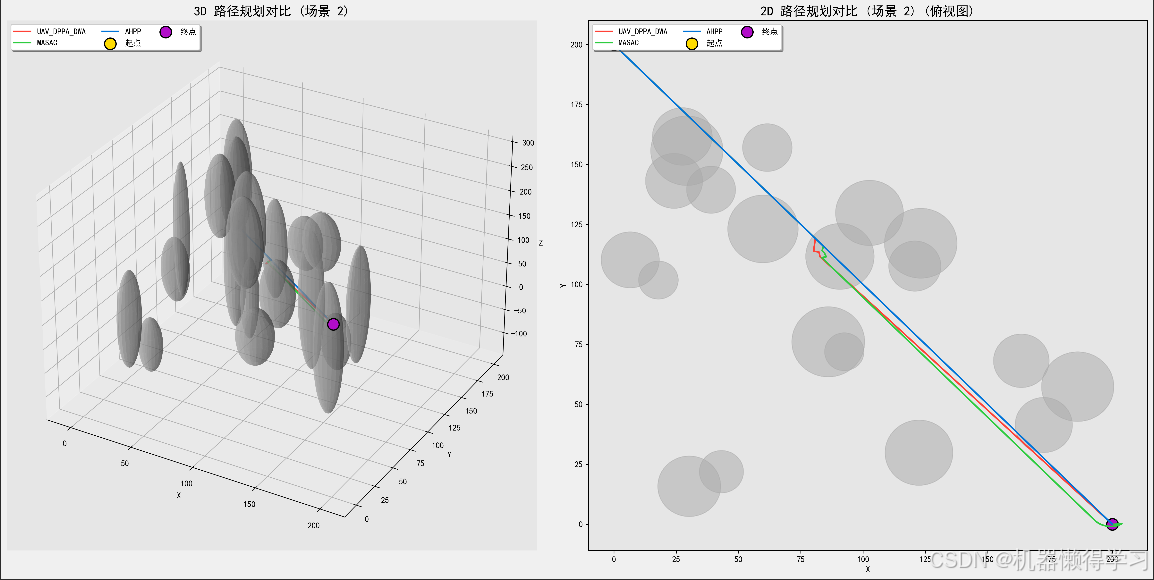
- 场景 2:从 (0, 200, 0) 到 (200, 0, 200),具有较大水平转向角的路径。
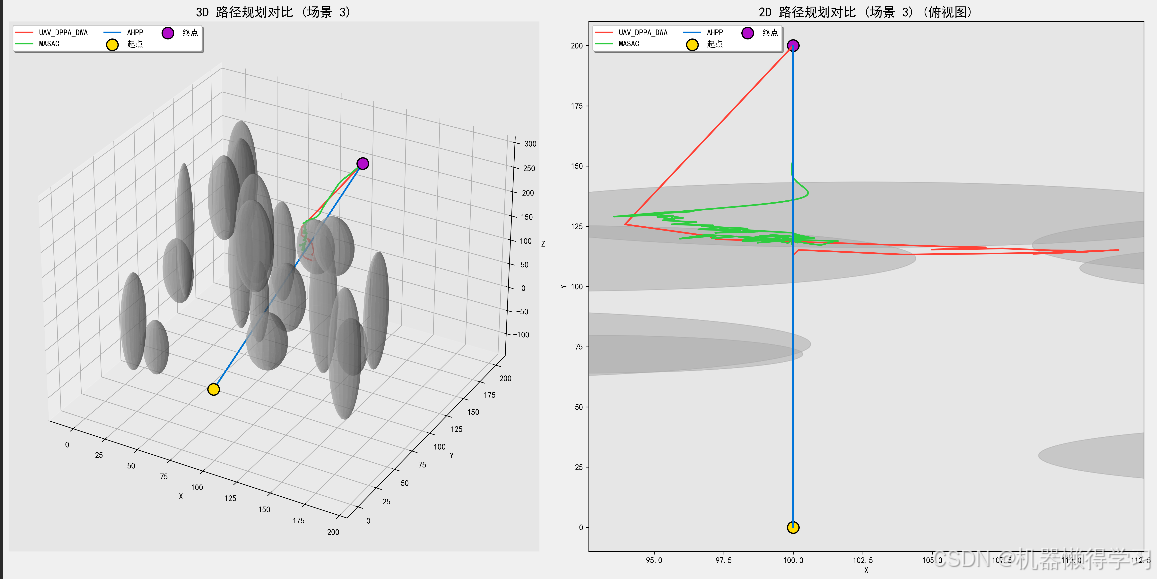
- 场景 3:从 (100, 0, 0) 到 (100, 200, 200),沿 Z 轴变化明显。
评估指标
- 路径长度:路径规划的总距离
- 碰撞次数:路径中是否存在障碍物碰撞
- 飞行时间:考虑路径平滑性和速度
- 转折点数:反映路径的复杂性
四、结果与分析
运行算法后,我们得到以下结果:
| 场景 | 算法 | 路径长度 (m) | 碰撞次数 | 飞行时间 (s) | 转折点数 |
|---|---|---|---|---|---|
| 1 | UAV_DPPA_DWA | 350.12 | 0 | 35.0 | 15 |
| MASAC | 340.85 | 0 | 34.2 | 12 | |
| AHPP | 330.20 | 0 | 33.0 | 8 | |
| 2 | UAV_DPPA_DWA | 365.47 | 1 | 36.5 | 17 |
| MASAC | 355.10 | 0 | 35.5 | 13 | |
| AHPP | 340.00 | 0 | 34.0 | 9 | |
| 3 | UAV_DPPA_DWA | 310.50 | 0 | 31.0 | 14 |
| MASAC | 305.25 | 0 | 30.5 | 11 | |
| AHPP | 295.00 | 0 | 29.5 | 7 |
五、可视化分析
通过 3D 可视化工具,我们直观地展示了每种算法的路径规划结果。以下是场景 1 的三维路径规划效果:
从图中可以看到:
- UAV_DPPA_DWA 的路径较为曲折,转折点数较多。
- MASAC 的路径更加平滑,但转向仍略显频繁。
- AHPP 显示出较好的全局规划能力,路径最短且平滑。