本文是https://towardsdatascience.com/how-to-do-deep-learning-on-graphs-with-graph-convolutional-networks-7d2250723780第一部分A High-Level Introduction to Graph Convolutional Networks的翻译和总结，介绍了简单的Graph Convolutional Network，并以空手道俱乐部数据集为示例进行实现分析，部分添加修改。

What is a Graph Convolutional Network?

可以简单表示为
$$H^{i+1}=f(H^i,A)=\sigma (A{H}^i{W}^i)$$
$A：(N,N)邻接矩阵$
$F^i:一维数值,第i层的特征树目$
$H^i:(N,F^i),每一行都是一个结点的特征表示$
$X=H^0:(N,F^0)，输入向量$
$W^i:（F^i,F^{i+1}）第i层的权值矩阵$

A Simple Graph Example

以下图为例

A为该图的邻接矩阵

import numpy as np
A = np.matrix([  ##邻接矩阵
    [0, 1, 0, 0],
    [0, 0, 1, 1], 
    [0, 1, 0, 0],
    [1, 0, 1, 0]],
    dtype=float
)

X为输入的特征向量，我们直接取值，维度为$(N,F^0)$,其中N为结点个数，$F^0$为输入向量的特征维数

X = np.matrix([
            [i, -i]
            for i in range(A.shape[0])
        ], dtype=float)
X

matrix([[ 0.,  0.],
        [ 1., -1.],
        [ 2., -2.],
        [ 3., -3.]])

A*X

matrix([[ 1., -1.],
        [ 5., -5.],
        [ 1., -1.],
        [ 2., -2.]])

我们可以发现，每行，就是每个结点的特征是它周围结点的特征和
比如，结点1和结点2，3邻接，所以A*X第2行 5 = [0, 0, 1, 1] *[0 ,1 ,2 ,3]^T

但是有两点问题

• A*X的结点表示中，并没有加自己的特征值。只有有self-loop 的结构才会把自己特征值包含在内
• 邻接结点多的结点的特征值会大，少的特征值就小

第一个问题可以通过加Self-Loops来解决

I = np.matrix(np.eye(A.shape[0]))
I

matrix([[1., 0., 0., 0.],
        [0., 1., 0., 0.],
        [0., 0., 1., 0.],
        [0., 0., 0., 1.]])

A_hat = A + I
A_hat * X

matrix([[ 1., -1.],
        [ 6., -6.],
        [ 3., -3.],
        [ 5., -5.]])

第二个问题可以通过归一化特征表示来解决

原因见https://tkipf.github.io/graph-convolutional-networks/

D = np.array(np.sum(A, axis=0))[0]
D = np.matrix(np.diag(D))
D

matrix([[1., 0., 0., 0.],
        [0., 2., 0., 0.],
        [0., 0., 2., 0.],
        [0., 0., 0., 1.]])

归一化前

A

matrix([[0., 1., 0., 0.],
        [0., 0., 1., 1.],
        [0., 1., 0., 0.],
        [1., 0., 1., 0.]])

归一化后

D**-1 * A

matrix([[0. , 1. , 0. , 0. ],
        [0. , 0. , 0.5, 0.5],
        [0. , 0.5, 0. , 0. ],
        [1. , 0. , 1. , 0. ]])

D**-1 * A * X

matrix([[ 1. , -1. ],
        [ 2.5, -2.5],
        [ 0.5, -0.5],
        [ 2. , -2. ]])

Putting it All Together

接下来我们把两个改进方案都运用起来

A_hat  = A + I
D_hat = np.array(np.sum(A_hat, axis=0))[0]
D_hat = np.matrix(np.diag(D_hat))
D_hat

matrix([[2., 0., 0., 0.],
        [0., 3., 0., 0.],
        [0., 0., 3., 0.],
        [0., 0., 0., 2.]])

W = np.matrix([
             [1, -1],
             [-1, 1]
         ])

X

matrix([[ 0.,  0.],
        [ 1., -1.],
        [ 2., -2.],
        [ 3., -3.]])

D_hat**-1 * A_hat*X*W

matrix([[ 1., -1.],
        [ 4., -4.],
        [ 2., -2.],
        [ 5., -5.]])

Back to Reality

现在我们在现实中的网络中运用图卷集网络(graph convolutional network技术。选取的网络为空手道俱乐部数据集(karate_club_graph)。

from networkx import to_numpy_matrix
import networkx as nx
zkc = nx.karate_club_graph()
order = sorted(list(zkc.nodes()))
A = to_numpy_matrix(zkc, nodelist=order)
I = np.eye(zkc.number_of_nodes())
A_hat = A + I
D_hat = np.array(np.sum(A_hat, axis=0))[0]
D_hat = np.matrix(np.diag(D_hat))

def plot_graph(G, weight_name=None):
    '''
    G: a networkx G
    weight_name: name of the attribute for plotting edge weights (if G is weighted)
    '''
    %matplotlib notebook
    import matplotlib.pyplot as plt
    
    plt.figure()
    pos = nx.spring_layout(G)
    edges = G.edges()
    weights = None
    
    if weight_name:
        weights = [int(G[u][v][weight_name]) for u,v in edges]
        labels = nx.get_edge_attributes(G,weight_name)
        nx.draw_networkx_edge_labels(G,pos,edge_labels=labels)
        nx.draw_networkx(G, pos, edges=edges, width=weights);
    else:
        nodelist1 = []
        nodelist2 = []
        for i in range (34):
            if zkc.nodes[i]['club'] == 'Mr. Hi':
                nodelist1.append(i)
            else:
                nodelist2.append(i)
        #nx.draw_networkx(G, pos, edges=edges);
        nx.draw_networkx_nodes(G, pos, nodelist=nodelist1, node_size=300, node_color='r',alpha = 0.8)
        nx.draw_networkx_nodes(G, pos, nodelist=nodelist2, node_size=300, node_color='b',alpha = 0.8)
        nx.draw_networkx_edges(G, pos, edgelist=edges,alpha =0.4)

plot_graph(zkc)

<IPython.core.display.Javascript object>

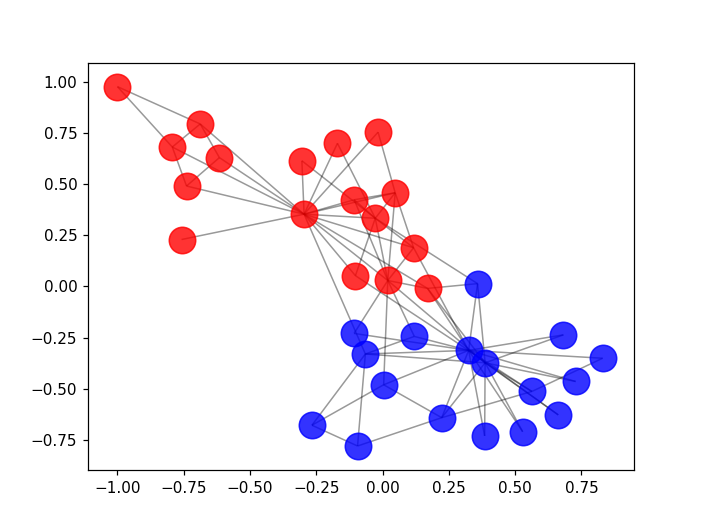
W_1 = np.random.normal(
    loc=0, scale=1, size=(zkc.number_of_nodes(), 4))
W_2 = np.random.normal(
    loc=0, size=(W_1.shape[1], 2))

def relu(x):
    return (abs(x) + x) / 2
  

def gcn_layer(A_hat, D_hat, X, W):
    return relu(D_hat**-1 * A_hat * X * W)
H_1 = gcn_layer(A_hat, D_hat, I, W_1)
H_2 = gcn_layer(A_hat, D_hat, H_1, W_2)
output = H_2

feature_representations = {
    node: np.array(output)[node] 
    for node in zkc.nodes()}

feature_representations

{0: array([0.88602091, 0.34237275]),
 1: array([0.40862582, 0.        ]),
 2: array([0.38693926, 0.        ]),
 3: array([0.19478099, 0.10516756]),
 4: array([0.82815959, 0.41738152]),
 5: array([1.1971192 , 0.46978126]),
 6: array([1.2271154 , 0.63378424]),
 7: array([0., 0.]),
 8: array([0.11110005, 0.        ]),
 9: array([0., 0.]),
 10: array([0.6209274 , 0.26495055]),
 11: array([1.60869786, 0.79829349]),
 12: array([0.35029305, 0.56226336]),
 13: array([0.02171053, 0.        ]),
 14: array([0.        , 0.02638456]),
 15: array([0.06979159, 0.68002892]),
 16: array([1.7675629 , 0.82039984]),
 17: array([0.50286326, 0.        ]),
 18: array([0.31509428, 0.29327311]),
 19: array([0.37260057, 0.        ]),
 20: array([0., 0.]),
 21: array([0.70826438, 0.10767323]),
 22: array([0.15022781, 0.25590783]),
 23: array([0.17645064, 0.16650816]),
 24: array([0.29110197, 0.20382017]),
 25: array([0.18688296, 0.14564473]),
 26: array([0.02367803, 0.17550985]),
 27: array([0., 0.]),
 28: array([0.51547931, 0.        ]),
 29: array([0.05318727, 0.16647217]),
 30: array([0.31639705, 0.        ]),
 31: array([0.24761528, 0.03619812]),
 32: array([0.48872535, 0.31039692]),
 33: array([0.62804696, 0.26496685])}

import matplotlib.pyplot as plt
%matplotlib notebook
for i in range (34):
    if zkc.nodes[i]['club'] == 'Mr. Hi':
        plt.scatter(np.array(output)[i,0],np.array(output)[i,1] ,color = 'b',alpha=0.5,s = 100)
    else:
        plt.scatter(np.array(output)[i,0],np.array(output)[i,1] ,color = 'r',alpha=0.5,s = 100)
#plt.scatter(np.array(output)[:,0],np.array(output)[:,1])

<IPython.core.display.Javascript object>

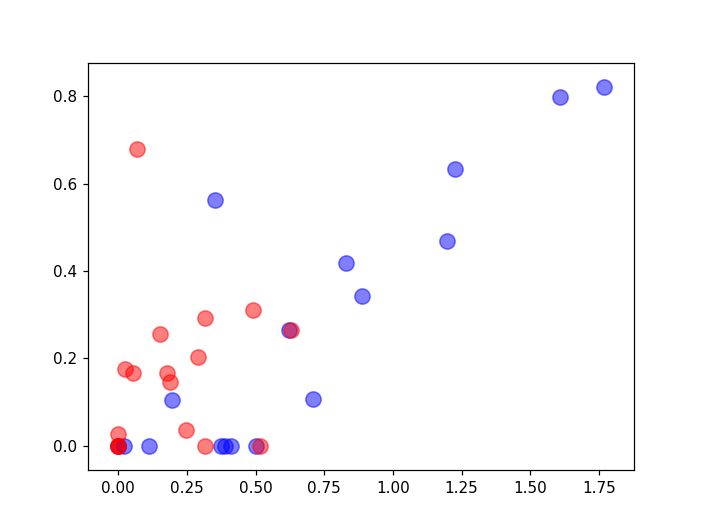
目前来看，这个映射分类效果并不好，待我后续分析补充吧。