本系列为《模式识别与机器学习》的读书笔记。
一,线性基函数模型
1,线性基函数
回归问题的⽬标是在给定 D D D 维输⼊(input) 变量 x \boldsymbol{x} x 的情况下, 预测⼀个或者多个连续⽬标(target)变量 t t t 的值。
通过将⼀组输⼊变量的⾮线性函数进⾏线性组合, 我们可以获得⼀类更加有⽤的函数, 被称为基函数(basis function)。
回归问题的最简单模型是输⼊变量的线性组合:
y ( x , w ) = w 0 + w 1 x 1 + ⋯ + w D x D (3.1) y(\boldsymbol{x},\boldsymbol{w}) = w_0+w_1x_1+\dots+w_Dx_D\tag{3.1} y(x,w)=w0+w1x1+⋯+wDxD(3.1)
其中, x = ( x 1 , x 2 , … , x D ) T \boldsymbol{x}=(x_1,x_2,\dots,x_D)^T x=(x1,x2,…,xD)T ,通常称为线性回归(linear regression),这个模型的关键性质在于它是参数 w 0 , … , w D w_0 ,\dots ,w_D w0,…,wD 的⼀个线性函数。 但是, 它也是输⼊变量 x i x_i xi 的⼀个线性函数, 这给模型带来了极⼤的局限性。因此扩展模型的类别:将输⼊变量的固定的⾮线性函数进⾏线性组合:
y ( x , w ) = w 0 + ∑ j = 1 M − 1 w j ϕ j ( x ) (3.2) y(\boldsymbol{x},\boldsymbol{w}) = w_0+\sum_{j=1}^{M-1}w_{j}\phi_{j}(\boldsymbol{x})\tag{3.2} y(x,w)=w0+j=1∑M−1wjϕj(x)(3.2)
其中, ϕ j ( x ) \phi_{j}(\boldsymbol{x}) ϕj(x) 被称为基函数(basis function),参 数 w 0 w_0 w0 使得数据中可以存在任意固定的偏 置,这个值通常被称为偏置参数(bias parameter)。此模型称为线性模型。
通常,定义⼀个额外的虚“基函数” ϕ 0 ( x ) = 1 \phi_{0}(\boldsymbol{x}) = 1 ϕ0(x)=1 是很⽅便的,这时,
y ( x , w ) = ∑ j = 0 M − 1 w j ϕ j ( x ) = w T ϕ ( x ) (3.3) y(\boldsymbol{x},\boldsymbol{w}) = \sum_{j=0}^{M-1}w_{j}\phi_{j}(\boldsymbol{x}) = \boldsymbol{w}^{T}\boldsymbol{\phi}(\boldsymbol{x})\tag{3.3} y(x,w)=j=0∑M−1wjϕj(x)=wTϕ(x)(3.3)
其中, w = ( w 0 , x 1 , … , w M − 1 ) T \boldsymbol{w}=(w_0,x_1,\dots,w_{M-1})^T w=(w0,x1,…,wM−1)T , ϕ = ( ϕ 0 , ϕ 2 , … , ϕ M − 1 ) T \boldsymbol{\phi}=(\phi_0,\phi_2,\dots,\phi_{M-1})^T ϕ=(ϕ0,ϕ2,…,ϕM−1)T 。
在许多模式识别的实际应⽤中, 我们会对 原始的数据变量进⾏某种固定形式的预处理或者特征抽取。如果原始变量由向量 x \boldsymbol{x} x 组成,那么特征可以⽤基函数 { ϕ j ( x ) } \{\phi_{j}(\boldsymbol{x})\} { ϕj(x)} 来表⽰。
多项式基函数的⼀个局限性在于它们是输⼊变量的全局函数,因此对于输⼊空间⼀个区域的改变将会影响所有其他的区域。这个问题的解决方案:把输⼊空间切分成若⼲个区域,然后对于每个区域⽤不同的多项式函数拟合,这样的函数叫做样条函数(spline function)(Hastie et al., 2001)。
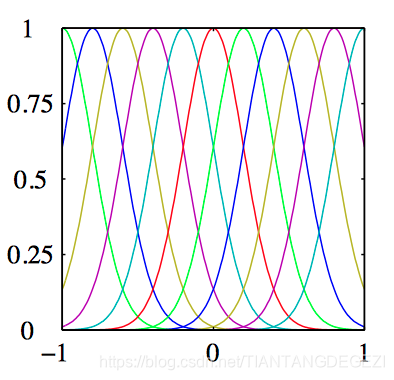
⾼斯基函数:
ϕ j ( x ) = exp { − ( x − μ j ) 2 2 s 2 } (3.4) \phi_{j}(x)=\exp\left\{-\frac{(x-\mu_{j})^2}{2s^{2}}\right\}\tag{3.4} ϕj(x)=exp{
−2s2(x−μj)2}(3.4)
其中, μ j \mu_{j} μj 控制了基函数在输⼊空间中的位置,参数 s s s 控制了基函数的空间⼤⼩。
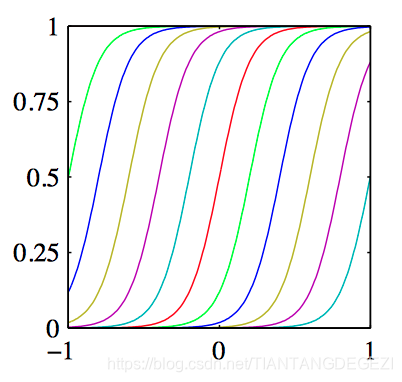
sigmoid基函数:
ϕ j ( x ) = σ ( x − μ j s ) (3.5) \phi_{j}(x)=\sigma\left(\frac{x-\mu_{j}}{s}\right)\tag{3.5} ϕj(x)=σ(sx−μj)(3.5)
其中 σ ( a ) \sigma(a) σ(a) 是 logistic sigmoid函数,定义为:
σ a = 1 1 + exp ( − a ) (3.6) \sigma_{a}=\frac{1}{1+\exp(-a)}\tag{3.6} σa=1+exp(−a)1(3.6)
除此之外,基函数还可以选择傅⾥叶基函数,tanh函数等等。其中,tanh函数 和 logistic sigmoid函数 的关系如下: tanh ( a ) = 2 σ ( 2 a ) − 1 \tanh(a)=2\sigma(2a)-1 tanh(a)=2σ(2a)−1。
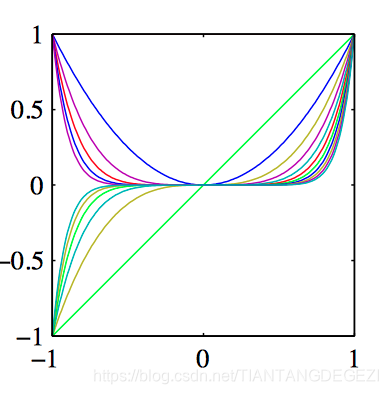
如图3.1~3.3,分别为是多项式基函数,⾼斯基函数,sigmoid基函数。
2,最⼤似然与最⼩平⽅
假设⽬标变量 t t t 由确定的函数 y ( x , w ) y(\boldsymbol{x},\boldsymbol{w}) y(x,w) 给出,这个函数被附加了⾼斯噪声,即
t = y ( x , w ) + ϵ t=y(\boldsymbol{x},\boldsymbol{w})+\epsilon t=y(x,w)+ϵ
其中, ϵ \epsilon ϵ 是⼀个零均值的⾼斯随机变量,精度(⽅差的倒数)为 β \beta β,则有:
p ( t ∣ x , w , β ) = N ( t ∣ y ( x , w ) , β − 1 ) (3.7) p(t|\boldsymbol{x},\boldsymbol{w},\beta)=\mathcal{N}(t|y(\boldsymbol{x},\boldsymbol{w}),\beta^{-1})\tag{3.7} p(t∣x,w,β)=N(t∣y(x,w),β−1)(3.7)
均值为:
E [ t ∣ x ] = ∫ t p ( t ∣ x ) d t = y ( x , w ) \mathbb{E}[t|\boldsymbol{x}]=\int tp(t|\boldsymbol{x})\mathrm{d}t=y(\boldsymbol{x},\boldsymbol{w}) E[t∣x]=∫tp(t∣x)dt=y(x,w)
考虑⼀个输⼊数据集 X = { x 1 , … , x N } \mathbf{X}=\{\boldsymbol{x}_1,\dots, \boldsymbol{x}_N\} X={
x1,…,xN}, 对应的⽬标值为 t 1 , … , t N t_1,\dots , t_N t1,…,tN 。 我们把⽬标向量 { t n } \{t_n\} {
tn} 组成⼀个列向量, 记作 t \mathbf{t} t。 假设这些数据点是独⽴地从分布公式(3.7)中抽取的,那么可以得到下⾯的似然函数的表达式, 它是可调节参数 w \boldsymbol{w} w 和 β \beta β 的函数,形式为:
p ( t ∣ X , w , β ) = ∏ n = 1 N N ( t n ∣ w T ϕ ( x n ) , β − 1 ) (3.8) p(\mathbf{t}|\mathbf{X},\boldsymbol{w},\beta)=\prod_{n=1}^{N}\mathcal{N}(t_{n}|\boldsymbol{w}^{T}\boldsymbol{\phi}(\boldsymbol{x}_{n}),\beta^{-1})\tag{3.8} p(t∣X,w,β)=n=1∏NN(tn∣wTϕ(xn),β−1)(3.8)
取似然函数的对数,使⽤⼀元⾼斯分布的标准形式,可得:
ln p ( t ∣ w , β ) = ∑ n = 1 N ln N ( t n ∣ w T ϕ ( x n ) , β − 1 )