🎉AI学习星球推荐: GoAI的学习社区 知识星球是一个致力于提供《机器学习 | 深度学习 | CV | NLP | 大模型 | 多模态 | AIGC 》各个最新AI方向综述、论文等成体系的学习资料,配有全面而有深度的专栏内容,包括不限于 前沿论文解读、资料共享、行业最新动态以、实践教程、求职相关(简历撰写技巧、面经资料与心得)多方面综合学习平台,强烈推荐AI小白及AI爱好者学习,性价比非常高!加入星球➡️点击链接
✨专栏介绍: 本作者推出全新系列《深入浅出LLM》专栏,将分为基础篇、进阶篇、实战篇等,本文为基础篇具体章节如导图所示(导图为常见LLM问题,导图专栏后续更新!),将分别从各个大模型模型的概念、经典模型、创新点、微调、分布式训练、数据集、未来发展方向、RAG、Agent及项目实战等各种角度展开详细介绍,欢迎大家关注。
💙作者主页: GoAI |💚 公众号: GoAI的学习小屋 | 💛交流群: 704932595 |💜个人简介 : 掘金签约作者、百度飞桨PPDE、领航团团长、开源特训营导师、CSDN、阿里云社区人工智能领域博客专家、新星计划计算机视觉方向导师等,专注大数据与AI 知识分享。
《深入浅出LLM基础篇》目录
《深入浅出LLM基础篇》(一):大模型概念与发展
《深入浅出LLM基础篇》(二):大模型基础知识
《深入浅出LLM基础篇》(三):大模型结构分类 (本篇)
《深入浅出LLM基础篇》(三):大模型结构分类
导读:本篇为《深入浅出LLM基础篇》系列第三篇,《深入浅出LLM基础篇》(三):大模型结构分类主要讨论大型语言模型是如何构建的,章节将着重讨论模型架构,主要讨论Transformer架构及编码、解码器组成结构及原理,这是真正实现大型语言模型的建模创新。
3.1 大模型概括
为了更好的了解整体的功能结构(而不从一开始就陷入局部的结构细节),我们一开始先将语言模型(model)的看作一个黑箱(black box)(在后续的内容中再逐步的拆解),从形象化的概念理解上来说当前大语言模型(大:体现中模型的规模上)的能力,其可以根据输入需求的语言描述(prompt)生成符合需求的结果(completion),形式可以表达为:
p r o m p t ⇝ m o d e l c o m p l e t i o n o r m o d e l ( p r o m p t ) = c o m p l e t i o n prompt \overset{model}{\leadsto} completion \ \ or \ \ model(prompt) = completion prompt⇝modelcompletion or model(prompt)=completion
接下来我们将从大语言模型的训练数据(traning data)分析开始接下来的内容,首先给出如下的形式化描述
t r a i n i n g d a t a ⇒ p ( x 1 , . . . , x L ) . training\ data \Rightarrow p(x_{1},...,x_{L}). training data⇒p(x1,...,xL).
3.2 模型架构
到目前为止,我们已经将语言模型定义为对词元序列的概率分布 p ( x 1 , … , x L ) p(x_{1},…,x_{L}) p(x1,…,xL),我们已经看到这种定义非常优雅且强大(通过提示,语言模型原则上可以完成任何任务,正如GPT-3所示)。然而,在实践中,对于专门的任务来说,避免生成整个序列的生成模型可能更高效。
上下文向量表征 (Contextual Embedding): 作为先决条件,主要的关键发展是将词元序列与相应的上下文的向量表征:
[ t h e , m o u s e , a t e , t h e , c h e e s e ] ⇒ ϕ [ ( 1 0.1 ) , ( 0 1 ) , ( 1 1 ) , ( 1 − 0.1 ) , ( 0 − 1 ) ] . [the, mouse, ate, the, cheese] \stackrel{\phi}{\Rightarrow}\left[\left(\begin{array}{c} 1 \\ 0.1 \end{array}\right),\left(\begin{array}{l} 0 \\ 1 \end{array}\right),\left(\begin{array}{l} 1 \\ 1 \end{array}\right),\left(\begin{array}{c} 1 \\ -0.1 \end{array}\right),\left(\begin{array}{c} 0 \\ -1 \end{array}\right)\right]. [the,mouse,ate,the,cheese]⇒ϕ[(10.1),(01),(11),(1−0.1),(0−1)].
正如名称所示,词元的上下文向量表征取决于其上下文(周围的单词);例如,考虑mouse的向量表示需要关注到周围某个窗口大小的其他单词。
-
符号表示:我们将 ϕ : V L → R d × L ϕ:V^{L}→ℝ^{d×L} ϕ:VL→Rd×L 定义为嵌入函数(类似于序列的特征映射,映射为对应的向量表示)。
-
对于词元序列 x 1 : L = [ x 1 , … , x L ] x1:L=[x_{1},…,x_{L}] x1:L=[x1,…,xL], ϕ ϕ ϕ 生成上下文向量表征 ϕ ( x 1 : L ) ϕ(x_{1:L}) ϕ(x1:L)。
3.3 大模型分类
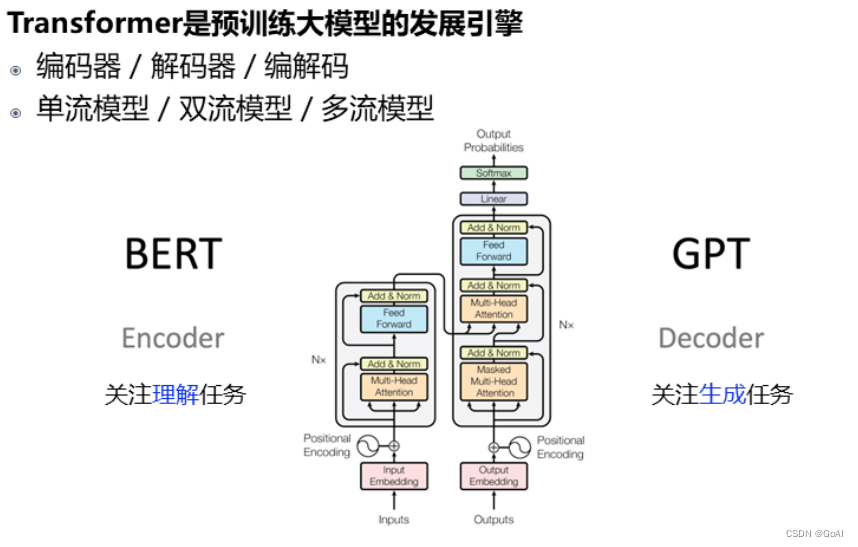
基于Transformer结构的模型又可以分为编码端(Encoder-Only),解码端(Decoder-Only)和编码-解码端(Encoder-Decoder)三类,具体如下图所示。
1.Encoder-Only架构:
定义与特点:这类模型仅包含编码器部分,主要用于从输入数据提取特征或表示。例如,在BERT (Bidirectional Encoder
Representations from Transformers)
中,它是一个双向Transformer编码器,被训练来理解文本上下文信息,并输出一个固定长度的向量表示,该表示包含了原始输入序列的丰富语义信息。
用途:主要用于预训练模型,如BERT、RoBERTa等,常用于各种下游任务的特征提取,比如分类、问答、命名实体识别等,但不直接用于生成新的序列。
仅编码器架构(Encoder-only):自编码模型(破坏一个句子,然后让模型去预测或填补),更擅长理解类的任务,例如:文本分类、实体识别、关键信息抽取等。典型代表有:Bert、RoBERTa等。
2.Decoder-Only架构:
定义与特点:解码器仅架构专注于从某种内部状态或先前生成的内容生成新的序列,通常用于自回归式预测任务,其中每个时刻的输出都依赖于前面生成的所有内容。
优点:强大的序列生成能力,能够按顺序逐个生成连续的元素(如单词、字符),适用于诸如文本生成、自动摘要、对话系统等生成性任务。典型的Decoder-Only模型包括GPT系列(如GPT-3)。
仅解码器架构(Decoder-only):自回归模型(将解码器自己当前步的输出加入下一步的输入,解码器融合所有已经输入的向量来输出下一个向量,所以越往后的输出考虑了更多输入),更擅长生成类的任务,例如:文本生成。典型代表有:GPT系列、LLaMA、OPT、Bloom等。
3.Encoder-Decoder架构:
定义与特点:这种架构由两个主要部分组成:编码器和解码器。编码器负责将输入序列转换为压缩的中间表示,解码器则基于这个中间表示生成目标输出序列。这种结构非常适合翻译、摘要生成、图像描述等任务,需要理解和重构输入信息后生成新序列的任务。
工作原理:编码器对源序列进行处理并生成上下文向量,解码器根据此上下文向量逐步生成目标序列。例如,经典的Seq2Seq(Sequence-to-Sequence)模型和Transformer中的机器翻译模型就采用了这样的结构。
编码器-解码器架构(Encoder-Decoder):序列到序列模型(编码器的输出作为解码器的输入),主要用于基于条件的生成任务,例如:翻译,概要等。典型代表有:T5、BART、GLM等。
3.3.1 结构详细介绍
编码端(Encoder-Only)架构
编码端架构的著名的模型如BERT、RoBERTa等。这些语言模型生成上下文向量表征,但不能直接用于生成文本。可以表示为, x 1 : L ⇒ ϕ ( x 1 : L ) x_{1:L}⇒ϕ(x_{1:L}) x1:L⇒ϕ(x1:L) 。这些上下文向量表征通常用于分类任务(也呗称为自然语言理解任务)。任务形式比较简单,下面以情感分类/自然语言推理任务举例:
情感分析输入与输出形式: [ [ C L S ] , 他们 , 移动 , 而 , 强大 ] ⇒ 正面情绪 情感分析输入与输出形式:[[CLS], 他们, 移动, 而, 强大]\Rightarrow 正面情绪 情感分析输入与输出形式:[[CLS],他们,移动,而,强大]⇒正面情绪
自然语言处理输入与输出形式: [ [ C L S ] , 所有 , 动物 , 都 , 喜欢 , 吃 , 饼干 , 哦 ] ⇒ 蕴涵 自然语言处理输入与输出形式:[[CLS], 所有, 动物, 都, 喜欢, 吃, 饼干, 哦]⇒蕴涵 自然语言处理输入与输出形式:[[CLS],所有,动物,都,喜欢,吃,饼干,哦]⇒蕴涵
该架构的优势是对于文本的上下文信息有更好的理解,因此该模型架构才会多用于理解任务。该架构的有点是对于每个 x i x{i} xi ,上下文向量表征可以双向地依赖于左侧上下文 ( x 1 : i − 1 ) (x_{1:i−1}) (x1:i−1) 和右侧上下文 ( x i + 1 : L ) (x_{i+1:L}) (xi+1:L) 。但是缺点在于不能自然地生成完成文本,且需要更多的特定训练目标(如掩码语言建模)。
解码器(Decoder-Only)架构
解码器架构的著名模型就是大名鼎鼎的GPT系列模型。这些是我们常见的自回归语言模型,给定一个提示
x
1
:
i
x_{1:i}
x1:i ,它们可以生成上下文向量表征,并对下一个词元
x
i
+
1
x_{i+1}
xi+1 (以及递归地,整个完成
x
i
+
1
:
L
x_{i+1:L}
xi+1:L) 生成一个概率分布。
x
1
:
i
⇒
ϕ
(
x
1
:
i
)
,
p
(
x
i
+
1
∣
x
1
:
i
)
x_{1:i}⇒ϕ(x_{1:i}),p(x_{i+1}∣x_{1:i})
x1:i⇒ϕ(x1:i),p(xi+1∣x1:i) 。我们以自动补全任务来说,输入与输出的形式为,
[
[
C
L
S
]
,
他们
,
移动
,
而
]
⇒
强大
[[CLS], 他们, 移动, 而]⇒强大
[[CLS],他们,移动,而]⇒强大 。与编码端架构比,其优点为能够自然地生成完成文本,有简单的训练目标(最大似然)。缺点也很明显,对于每个
x
i
xi
xi ,上下文向量表征只能单向地依赖于左侧上下文 (
x
1
:
i
−
1
x_{1:i−1}
x1:i−1) 。
编码-解码端(Encoder-Decoder)架构
编码-解码端架构就是最初的Transformer模型,其他的还有如BART、T5等模型。这些模型在某种程度上结合了两者的优点:它们可以使用双向上下文向量表征来处理输入 x 1 : L x_{1:L} x1:L ,并且可以生成输出 y 1 : L y_{1:L} y1:L 。可以公式化为:
x 1 : L ⇒ ϕ ( x 1 : L ) , p ( y 1 : L ∣ ϕ ( x 1 : L ) ) 。 x1:L⇒ϕ(x1:L),p(y1:L∣ϕ(x1:L))。 x1:L⇒ϕ(x1:L),p(y1:L∣ϕ(x1:L))。
以表格到文本生成任务为例,其输入和输出的可以表示为:
[ 名称 : , 植物 , ∣ , 类型 : , 花卉 , 商店 ] ⇒ [ 花卉 , 是 , 一 , 个 , 商店 ] 。 [名称:, 植物, |, 类型:, 花卉, 商店]⇒[花卉, 是, 一, 个, 商店]。 [名称:,植物,∣,类型:,花卉,商店]⇒[花卉,是,一,个,商店]。
该模型的具有编码端,解码端两个架构的共同的优点,对于每个 x i x_{i} xi ,上下文向量表征可以双向地依赖于左侧上下文 x 1 : i − 1 x_{1:i−1} x1:i−1 ) 和右侧上下文 ( x i + 1 : L x_{i+1:L} xi+1:L ),可以自由的生成文本数据。缺点就说需要更多的特定训练目标。
总结:
Encoder-Only用于理解输入并生成其抽象表示,不涉及序列生成。
Decoder-Only专门用于根据之前的信息自动生成新序列,不接收外部输入。
Encoder-Decoder结合了两者的功能,首先对输入进行编码,然后基于编码结果解码生成新序列。
3.3.2 语言模型理论
下一步,我们会介绍语言模型的模型架构,重点介绍Transformer架构机器延伸的内容。另外我们对于架构还会对于之前RNN网络的核心知识进行阐述,其目的是对于代表性的模型架构进行学习,为未来的内容增加知识储备。
深度学习的美妙之处在于能够创建构建模块,就像我们用函数构建整个程序一样。因此,在下面的模型架构的讲述中,我们能够像下面的函数一样封装,以函数的的方法进行理解:
T r a n s f o r m e r B l o c k ( x 1 : L ) TransformerBlock(x_{1:L}) TransformerBlock(x1:L)
为了简单起见,我们将在函数主体中包含参数,接下来,我们将定义一个构建模块库,直到构建完整的Transformer模型。
3.3.2.1 基础架构
首先,我们需要将词元序列转换为序列的向量形式。 E m b e d T o k e n EmbedToken EmbedToken 函数通过在嵌入矩阵 E ∈ R ∣ v ∣ × d E∈ℝ^{|v|×d} E∈R∣v∣×d 中查找每个词元所对应的向量,该向量的具体值这是从数据中学习的参数:
def E m b e d T o k e n ( x 1 : L : V L ) → R d × L EmbedToken(x_{1:L}:V^{L})→ℝ^{d×L} EmbedToken(x1:L:VL)→Rd×L :
- 将序列 x 1 : L x_{1:L} x1:L 中的每个词元 x i xi xi 转换为向量。
- 返回[Ex1,…,ExL]。
以上的词嵌入是传统的词嵌入,向量内容与上下文无关。这里我们定义一个抽象的 S e q u e n c e M o d e l SequenceModel SequenceModel 函数,它接受这些上下文无关的嵌入,并将它们映射为上下文相关的嵌入。
d e f S e q u e n c e M o d e l ( x 1 : L : R d × L ) → R d × L def SequenceModel(x_{1:L}:ℝ^{d×L})→ℝ^{d×L} defSequenceModel(x1:L:Rd×L)→Rd×L :
- 针对序列 x 1 : L x_{1:L} x1:L 中的每个元素xi进行处理,考虑其他元素。
- [抽象实现(例如, F e e d F o r w a r d S e q u e n c e M o d e l FeedForwardSequenceModel FeedForwardSequenceModel , S e q u e n c e R N N SequenceRNN SequenceRNN , T r a n s f o r m e r B l o c k TransformerBlock TransformerBlock )]
最简单类型的序列模型基于前馈网络(Bengio等人,2003),应用于固定长度的上下文,就像n-gram模型一样,函数的实现如下:
def F e e d F o r w a r d S e q u e n c e M o d e l ( x 1 : L : R d × L ) → R d × L FeedForwardSequenceModel(x_{1:L}:ℝ^{d×L})→ℝ^{d×L} FeedForwardSequenceModel(x1:L:Rd×L)→Rd×L :
- 通过查看最后 n n n 个元素处理序列 x 1 : L x_{1:L} x1:L 中的每个元素 x i xi xi 。
- 对于每个
i
=
1
,
…
,
L
i=1,…,L
i=1,…,L :
- 计算 h i h_{i} hi= F e e d F o r w a r d ( x i − n + 1 , … , x i ) FeedForward(x_{i−n+1},…,x_{i}) FeedForward(xi−n+1,…,xi) 。
- 返回[ h 1 , … , h L h_{1},…,h_{L} h1,…,hL ]。
3.3.2.2 递归神经网络
第一个真正的序列模型是递归神经网络(RNN),它是一类模型,包括简单的RNN、LSTM和GRU。基本形式的RNN通过递归地计算一系列隐藏状态来进行计算。
def S e q u e n c e R N N ( x : R d × L ) → R d × L SequenceRNN(x:ℝ^{d×L})→ℝ^{d×L} SequenceRNN(x:Rd×L)→Rd×L :
- 从左到右处理序列 x 1 , … , x L x_{1},…,x_{L} x1,…,xL ,并递归计算向量 h 1 , … , h L h_{1},…,h_{L} h1,…,hL 。
- 对于
i
=
1
,
…
,
L
i=1,…,L
i=1,…,L :
- 计算 h i = R N N ( h i − 1 , x i ) h_{i}=RNN(h_{i−1},x_{i}) hi=RNN(hi−1,xi) 。
- 返回 [ h 1 , … , h L ] [h_{1},…,h_{L}] [h1,…,hL] 。
实际完成工作的模块是RNN,类似于有限状态机,它接收当前状态h、新观测值x,并返回更新后的状态:
def R N N ( h : R d , x : R d ) → R d RNN(h:ℝ^d,x:ℝ^d)→ℝ^d RNN(h:Rd,x:Rd)→Rd :
- 根据新的观测值x更新隐藏状态h。
- [抽象实现(例如,SimpleRNN,LSTM,GRU)]
有三种方法可以实现RNN。最早的RNN是简单RNN(Elman,1990),它将 h h h和 x x x的线性组合通过逐元素非线性函数 σ σ σ (例如,逻辑函数 σ ( z ) = ( 1 + e − z ) − 1 σ(z)=(1+e−z)−1 σ(z)=(1+e−z)−1 或更现代的 R e L U ReLU ReLU 函数 σ ( z ) = m a x ( 0 , z ) σ(z)=max(0,z) σ(z)=max(0,z) )进行处理。
def S i m p l e R N N ( h : R d , x : R d ) → R d SimpleRNN(h:ℝd,x:ℝd)→ℝd SimpleRNN(h:Rd,x:Rd)→Rd :
- 通过简单的线性变换和非线性函数根据新的观测值 x x x 更新隐藏状态 h h h 。
- 返回 σ ( U h + V x + b ) σ(Uh+Vx+b) σ(Uh+Vx+b) 。
正如定义的RNN只依赖于过去,但我们可以通过向后运行另一个RNN来使其依赖于未来两个。这些模型被ELMo和ULMFiT使用。
def B i d i r e c t i o n a l S e q u e n c e R N N ( x 1 : L : R d × L ) → R 2 d × L BidirectionalSequenceRNN(x_{1:L}:ℝ^{d×L})→ℝ^{2d×L} BidirectionalSequenceRNN(x1:L:Rd×L)→R2d×L :
- 同时从左到右和从右到左处理序列。
- 计算从左到右: [ h → 1 , … , h → L ] ← S e q u e n c e R N N ( x 1 , … , x L ) [h→_{1},…,h→_{L}]←SequenceRNN(x_{1},…,x_{L}) [h→1,…,h→L]←SequenceRNN(x1,…,xL) 。
- 计算从右到左: [ h ← L , … , h ← 1 ] ← S e q u e n c e R N N ( x L , … , x 1 ) [h←_{L},…,h←_{1}]←SequenceRNN(x_{L},…,x_{1}) [h←L,…,h←1]←SequenceRNN(xL,…,x1) 。
- 返回 [ h → 1 h ← 1 , … , h → L h ← L ] [h→_{1}h←_{1},…,h→_{L}h←_{L}] [h→1h←1,…,h→Lh←L] 。
注:
- 简单RNN由于梯度消失的问题很难训练。
- 为了解决这个问题,发展了长短期记忆(LSTM)和门控循环单元(GRU)(都属于RNN)。
- 然而,即使嵌入h200可以依赖于任意远的过去(例如,x1),它不太可能以“精确”的方式依赖于它(更多讨论,请参见Khandelwal等人,2018)。
- 从某种意义上说,LSTM真正地将深度学习引入了NLP领域。
3.4 Transformer组成
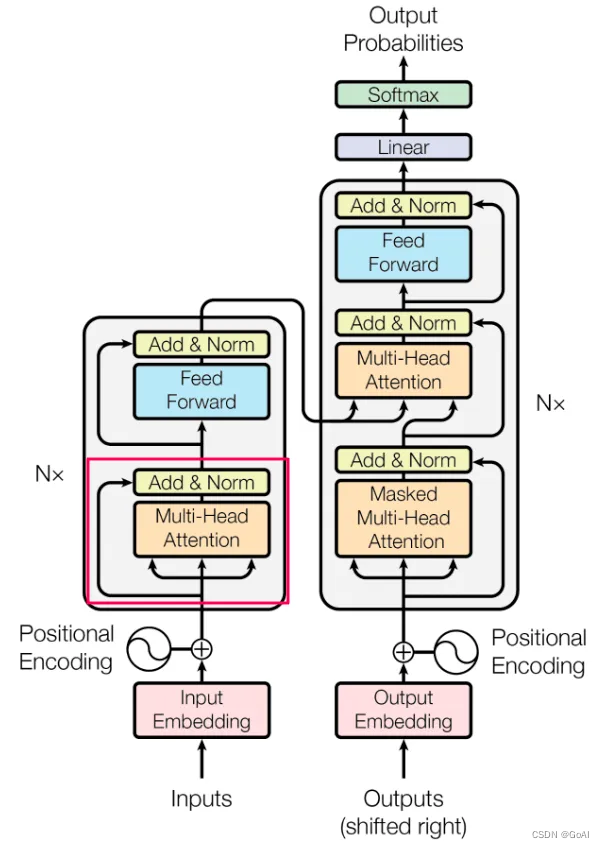
Transformer是一种由谷歌在2017年提出的深度学习模型,主要用于自然语言处理(NLP)任务,特别是序列到序列(Sequence-to-Sequence)的学习问题,如机器翻译、文本生成等。Transformer彻底改变了之前基于循环神经网络(RNNs)和长短期记忆网络(LSTMs)的序列建模范式,并且在性能上取得了显著提升。Transformer模型将其分解为Decoder-Only(GPT-2,GPT-3)、Encoder-Only(BERT,RoBERTa)和Encoder-Decoder(BART,T5)模型的构建模块。Transformer结构如下图所示:
Transformer的核心创新点包括:
自注意力机制(Self-Attention Mechanism):Transformer模型摒弃了传统RNN结构的时间依赖性,通过自注意力机制实现了对输入序列中任意两个位置之间的直接关联建模。每个词的位置可以同时关注整个句子中的其他所有词,计算它们之间的相关性得分,然后根据这些得分加权求和得到该位置的上下文向量表示。这种全局信息的捕获能力极大地提高了模型的表达力。
多头注意力(Multi-Head Attention):Transformer进一步将自注意力机制分解为多个并行的“头部”,每个头部负责从不同角度对输入序列进行关注,从而增强了模型捕捉多种复杂依赖关系的能力。最后,各个头部的结果会拼接并经过线性变换后得到最终的注意力输出。
位置编码(Positional Encoding):由于Transformer不再使用RNN那样的顺序处理方式,为了引入序列中词的位置信息,它采用了一种特殊的位置编码方法。这种方法对序列中的每个位置赋予一个特定的向量,这个向量的值与位置有关,确保模型在处理时能够区分不同的词语顺序。
编码器-解码器架构(Encoder-Decoder Architecture):Transformer采用了标准的编码器-解码器结构,其中编码器负责理解输入序列,将其转换成高级语义表示;而解码器则依据编码器的输出并结合自身产生的隐状态逐步生成目标序列。在解码过程中,解码器还应用了自注意力机制以及一种称为“掩码”(Masking)的技术来防止提前看到未来要预测的部分。
残差连接(Residual Connections):Transformer沿用了ResNet中的残差连接设计,以解决随着网络层数加深带来的梯度消失或爆炸问题,有助于训练更深更复杂的模型。
层归一化(Layer Normalization):Transformer使用了层归一化而非批量归一化,这使得模型在小批量训练时也能获得良好的表现,并且有利于模型收敛。
总结:
Transformer架构的核心组成:
- 自注意力机制(Self-Attention)和前馈神经网络(Feedforward Neural Networks),自注意力机制允许模型在处理每个单词时同时考虑到句子中的其他单词,从而捕捉更复杂的语言关系
- Layer Normalization和残差连接ADD,防止在深层网络中出现的梯度消失问题
- 位置编码:由于Transformer模型本身不处理序列中的位置信息,位置编码可以添加位置信息,对于理解文本顺序和语言结构至关重要。
关于Transformer的学习资源有很多:
- Illustrated Transformer和Illustrated GPT-2:对Transformer的视觉描述非常好。
- Annotated Transformer:Transformer的Pytorch实现。
强烈建议您阅读这些参考资料。该课程主要依据代码函数和接口进行讲解。
注意力机制
Transformer的关键是注意机制,这个机制早在机器翻译中就被开发出来了(Bahdananu等人,2017)。可以将注意力视为一个“软”查找表,其中有一个查询 $y $,我们希望将其与序列 x 1 : L = [ x 1 , … , x L ] x_{1:L}=[x_1,…,x_L] x1:L=[x1,…,xL] 的每个元素进行匹配。我们可以通过线性变换将每个 x i x_{i} xi 视为表示键值对:
( W k e y x i ) : ( W v a l u e x i ) (W_{key}x_{i}):(W_{value}x_{i}) (Wkeyxi):(Wvaluexi)
并通过另一个线性变换形成查询:
W q u e r y y W_{query}y Wqueryy
可以将键和查询进行比较,得到一个分数:
s c o r e i = x i ⊤ W k e y ⊤ W q u e r y y score_{i}=x^{⊤}_{i}W^{⊤}_{key}W_{query}y scorei=xi⊤Wkey⊤Wqueryy
这些分数可以进行指数化和归一化,形成关于词元位置 1 , … , L {1,…,L} 1,…,L的概率分布:
[ α 1 , … , α L ] = s o f t m a x ( [ s c o r e 1 , … , s c o r e L ] ) [α_{1},…,α_{L}]=softmax([score_{1},…,score_{L}]) [α1,…,αL]=softmax([score1,…,scoreL])
然后最终的输出是基于值的加权组合:
∑ i = 1 L α i ( W v a l u e x i ) \sum_{i=1}^L \alpha_i\left(W_{value} x_i\right) i=1∑Lαi(Wvaluexi)
我们可以用矩阵形式简洁地表示所有这些内容:
def A t t e n t i o n ( x 1 : L : R d × L , y : R d ) → R d Attention(x_{1:L}:ℝ^{d×L},y:ℝ^d)→ℝ^d Attention(x1:L:Rd×L,y:Rd)→Rd :
- 通过将其与每个 x i x_{i} xi进行比较来处理 y y y。
- 返回 W v a l u e x 1 : L softmax ( x 1 : L ⊤ W k e y ⊤ W q u e r y y / d ) W_{value} x_{1: L} \operatorname{softmax}\left(x_{1: L}^{\top} W_{key}^{\top} W_{query} y / \sqrt{d}\right) Wvaluex1:Lsoftmax(x1:L⊤Wkey⊤Wqueryy/d)
我们可以将注意力看作是具有多个方面(例如,句法、语义)的匹配。为了适应这一点,我们可以同时使用多个注意力头,并简单地组合它们的输出。
def M u l t i H e a d e d A t t e n t i o n ( x 1 : L : R d × L , y : R d ) → R d MultiHeadedAttention(x_{1:L}:ℝ^{d×L},y:ℝ^{d})→ℝ^{d} MultiHeadedAttention(x1:L:Rd×L,y:Rd)→Rd :
- 通过将其与每个xi与nheads个方面进行比较,处理y。
- 返回 W o u t p u t [ [ Attention ( x 1 : L , y ) , … , Attention ( x 1 : L , y ) ] ⏟ n h e a d s t i m e s W_{output}[\underbrace{\left[\operatorname{Attention}\left(x_{1: L}, y\right), \ldots, \operatorname{Attention}\left(x_{1: L}, y\right)\right]}_{n_{heads}times} Woutput[nheadstimes [Attention(x1:L,y),…,Attention(x1:L,y)]
对于自注意层,我们将用 x i x_{i} xi替换 y y y作为查询参数来产生,其本质上就是将自身的 x i x_{i} xi对句子的其他上下文内容进行 A t t e n t i o n Attention Attention 的运算:
def S e l f A t t e n t i o n ( x 1 : L : R d × L ) → R d × L ) SelfAttention(x_{1:L}:ℝ_{d×L})→ℝ_{d×L}) SelfAttention(x1:L:Rd×L)→Rd×L) :
- 将每个元素xi与其他元素进行比较。
- 返回 [ A t t e n t i o n ( x 1 : L , x 1 ) , … , A t t e n t i o n ( x 1 : L , x L ) ] [Attention(x_{1:L},x_{1}),…,Attention(x_{1:L},x_{L})] [Attention(x1:L,x1),…,Attention(x1:L,xL)] 。
自注意力使得所有的词元都可以“相互通信”,而前馈层提供进一步的连接:
def F e e d F o r w a r d ( x 1 : L : R d × L ) → R d × L FeedForward(x_{1:L}:ℝ^{d×L})→ℝ^{d×L} FeedForward(x1:L:Rd×L)→Rd×L :
- 独立处理每个词元。
- 对于
i
=
1
,
…
,
L
i=1,…,L
i=1,…,L :
- 计算 y i = W 2 m a x ( W 1 x i + b 1 , 0 ) + b 2 y_{i}=W_{2}max(W_{1}x_{i}+b_{1},0)+b_{2} yi=W2max(W1xi+b1,0)+b2 。
- 返回 [ y 1 , … , y L ] [y_{1},…,y_{L}] [y1,…,yL] 。
对于Transformer的主要的组件,我们差不多进行介绍。原则上,我们可以只需将 F e e d F o r w a r d ∘ S e l f A t t e n t i o n FeedForward∘SelfAttention FeedForward∘SelfAttention 序列模型迭代96次以构建GPT-3,但是那样的网络很难优化(同样受到沿深度方向的梯度消失问题的困扰)。因此,我们必须进行两个手段,以确保网络可训练。
残差连接和归一化
残差连接:计算机视觉中的一个技巧是残差连接(ResNet)。我们不仅应用某个函数f:
f
(
x
1
:
L
)
,
f(x1:L),
f(x1:L),
而是添加一个残差(跳跃)连接,以便如果
f
f
f的梯度消失,梯度仍然可以通过
x
1
:
L
x_{1:L}
x1:L 进行计算:
x 1 : L + f ( x 1 : L ) 。 x_{1:L}+f(x_{1:L})。 x1:L+f(x1:L)。
层归一化:另一个技巧是层归一化,它接收一个向量并确保其元素不会太大:
def L a y e r N o r m ( x 1 : L : R d × L ) → R d × L LayerNorm(x_{1:L}:ℝ^{d×L})→ℝ^{d×L} LayerNorm(x1:L:Rd×L)→Rd×L :
- 使得每个 x i x_{i} xi 既不太大也不太小。
我们首先定义一个适配器函数,该函数接受一个序列模型 f f f并使其“鲁棒”:
def A d d N o r m ( f : ( R d × L → R d × L ) , x 1 : L : R d × L ) → R d × L AddNorm(f:(ℝd^{×L}→ℝ^{d×L}),x_{1:L}:ℝ_{d×L})→ℝ^{d×L} AddNorm(f:(Rd×L→Rd×L),x1:L:Rd×L)→Rd×L :
- 安全地将f应用于 x 1 : L x_{1:L} x1:L 。
- 返回 L a y e r N o r m ( x 1 : L + f ( x 1 : L ) ) LayerNorm(x_{1:L}+f(x_{1:L})) LayerNorm(x1:L+f(x1:L)) 。
最后,我们可以简洁地定义Transformer块如下:
def T r a n s f o r m e r B l o c k ( x 1 : L : R d × L ) → R d × L TransformerBlock(x_{1:L}:ℝ^{d×L})→ℝ^{d×L} TransformerBlock(x1:L:Rd×L)→Rd×L :
- 处理上下文中的每个元素 x i x_{i} xi 。
- 返回 A d d N o r m ( F e e d F o r w a r d , A d d N o r m ( S e l f A t t e n t i o n , x 1 : L ) ) AddNorm(FeedForward,AddNorm(SelfAttention,x_{1:L})) AddNorm(FeedForward,AddNorm(SelfAttention,x1:L)) 。
位置嵌入
最后我们对目前语言模型的位置嵌入进行讨论。您可能已经注意到,根据定义,词元的嵌入不依赖于其在序列中的位置,因此两个句子中的𝗆𝗈𝗎𝗌𝖾将具有相同的嵌入,从而在句子位置的角度忽略了上下文的信息,这是不合理的。
[𝗍𝗁𝖾,𝗆𝗈𝗎𝗌𝖾,𝖺𝗍𝖾,𝗍𝗁𝖾,𝖼𝗁𝖾𝖾𝗌𝖾]
[𝗍𝗁𝖾,𝖼𝗁𝖾𝖾𝗌𝖾,𝖺𝗍𝖾,𝗍𝗁𝖾,𝗆𝗈𝗎𝗌𝖾]
为了解决这个问题,我们将位置信息添加到嵌入中:
def E m b e d T o k e n W i t h P o s i t i o n ( x 1 : L : R d × L ) EmbedTokenWithPosition(x_{1:L}:ℝ^{d×L}) EmbedTokenWithPosition(x1:L:Rd×L) :
- 添加位置信息。
- 定义位置嵌入:
- 偶数维度: P i , 2 j = s i n ( i / 1000 0 2 j / d m o d e l ) P_{i,2j}=sin(i/10000^{2j/dmodel}) Pi,2j=sin(i/100002j/dmodel)
- 奇数维度: P i , 2 j + 1 = c o s ( i / 1000 0 2 j / d m o d e l ) P_{i,2j+1}=cos(i/10000^{2j/dmodel}) Pi,2j+1=cos(i/100002j/dmodel)
- 返回 [ x 1 + P 1 , … , x L + P L ] [x_1+P_1,…,x_L+P_L] [x1+P1,…,xL+PL] 。
上面的函数中, i i i 表示句子中词元的位置, j j j 表示该词元的向量表示维度位置。
最后我们来聊一下GPT-3。在所有组件就位后,我们现在可以简要地定义GPT-3架构,只需将Transformer块堆叠96次即可:
G P T − 3 ( x 1 : L ) = T r a n s f o r m e r B l o c k 96 ( E m b e d T o k e n W i t h P o s i t i o n ( x 1 : L ) ) GPT-3(x_{1:L})=TransformerBlock^{96}(EmbedTokenWithPosition(x_{1:L})) GPT−3(x1:L)=TransformerBlock96(EmbedTokenWithPosition(x1:L))
架构的形状(如何分配1750亿个参数):
- 隐藏状态的维度:dmodel=12288
- 中间前馈层的维度:dff=4dmodel
- 注意头的数量:nheads=96
- 上下文长度:L=2048
这些决策未必是最优的。Levine等人(2020)提供了一些理论上的证明,表明GPT-3的深度太深,这促使了更深但更宽的Jurassic架构的训练。
不同版本的Transformer之间存在重要但详细的差异:
- 层归一化“后归一化”(原始Transformer论文)与“先归一化”(GPT-2),这影响了训练的稳定性(Davis等人,2021)。
- 应用了丢弃(Dropout)以防止过拟合。
- GPT-3使用了sparse Transformer(稀释 Transformer)来减少参数数量,并与稠密层交错使用。
- 根据Transformer的类型(Encdoer-Only, Decoder-Only, Encdoer-Decoder),使用不同的掩码操作。
3.5 扩展
分词:
- Between words and characters: A Brief History of Open-Vocabulary Modeling and Tokenization in NLP. Sabrina J. Mielke, Zaid Alyafeai, Elizabeth Salesky, Colin Raffel, Manan Dey, Matthias Gallé, Arun Raja, Chenglei Si, Wilson Y. Lee, Benoît Sagot, Samson Tan. 2021. Comprehensive survey of tokenization.
- Neural Machine Translation of Rare Words with Subword Units. Rico Sennrich, B. Haddow, Alexandra Birch. ACL 2015. Introduces byte pair encoding into NLP. Used by GPT-2, GPT-3.
- Google’s Neural Machine Translation System: Bridging the Gap between Human and Machine Translation. Yonghui Wu, M. Schuster, Z. Chen, Quoc V. Le, Mohammad Norouzi, Wolfgang Macherey, M. Krikun, Yuan Cao, Qin Gao, Klaus Macherey, J. Klingner, Apurva Shah, Melvin Johnson, Xiaobing Liu, Lukasz Kaiser, Stephan Gouws, Y. Kato, Taku Kudo, H. Kazawa, K. Stevens, George Kurian, Nishant Patil, W. Wang, C. Young, Jason R. Smith, Jason Riesa, Alex Rudnick, Oriol Vinyals, G. Corrado, Macduff Hughes, J. Dean. 2016. Introduces WordPiece. Used by BERT.
- SentencePiece: A simple and language independent subword tokenizer and detokenizer for Neural Text Processing. Taku Kudo, John Richardson. EMNLP 2018. Introduces SentencePiece.
模型架构:
- Language Models are Unsupervised Multitask Learners. Introduces GPT-2.
- Attention is All you Need. Ashish Vaswani, Noam M. Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N. Gomez, Lukasz Kaiser, Illia Polosukhin. NIPS 2017.
- Illustrated Transformer
- CS224N slides on RNNs
- CS224N slides on Transformers
- Train Short, Test Long: Attention with Linear Biases Enables Input Length Extrapolation. Ofir Press, Noah A. Smith, M. Lewis. 2021. Introduces Alibi embeddings.
- Transformer-XL: Attentive Language Models beyond a Fixed-Length Context. Zihang Dai, Zhilin Yang, Yiming Yang, J. Carbonell, Quoc V. Le, R. Salakhutdinov. ACL 2019. Introduces recurrence on Transformers, relative position encoding scheme.
- Generating Long Sequences with Sparse Transformers. R. Child, Scott Gray, Alec Radford, Ilya Sutskever. 2019. Introduces Sparse Transformers.
- Linformer: Self-Attention with Linear Complexity. Sinong Wang, Belinda Z. Li, Madian Khabsa, Han Fang, Hao Ma. 2020. Introduces Linformers.
- Rethinking Attention with Performers. K. Choromanski, Valerii Likhosherstov, David Dohan, Xingyou Song, Andreea Gane, Tamás Sarlós, Peter Hawkins, Jared Davis, Afroz Mohiuddin, Lukasz Kaiser, David Belanger, Lucy J. Colwell, Adrian Weller. ICLR 2020. Introduces Performers.
- Efficient Transformers: A Survey. Yi Tay, M. Dehghani, Dara Bahri, Donald Metzler. 2020.
Decoder-only 架构:
- Language Models are Unsupervised Multitask Learners. Alec Radford, Jeff Wu, R. Child, D. Luan, Dario Amodei, Ilya Sutskever. 2019. Introduces GPT-2 from OpenAI.
- Language Models are Few-Shot Learners. Tom B. Brown, Benjamin Mann, Nick Ryder, Melanie Subbiah, J. Kaplan, Prafulla Dhariwal, Arvind Neelakantan, Pranav Shyam, Girish Sastry, Amanda Askell, Sandhini Agarwal, Ariel Herbert-Voss, Gretchen Krueger, T. Henighan, R. Child, A. Ramesh, Daniel M. Ziegler, Jeff Wu, Clemens Winter, Christopher Hesse, Mark Chen, Eric Sigler, Mateusz Litwin, Scott Gray, Benjamin Chess, Jack Clark, Christopher Berner, Sam McCandlish, Alec Radford, Ilya Sutskever, Dario Amodei. NeurIPS 2020. Introduces GPT-3 from OpenAI.
- Scaling Language Models: Methods, Analysis&Insights from Training Gopher. Jack W. Rae, Sebastian Borgeaud, Trevor Cai, Katie Millican, Jordan Hoffmann, Francis Song, J. Aslanides, Sarah Henderson, Roman Ring, Susannah Young, Eliza Rutherford, Tom Hennigan, Jacob Menick, Albin Cassirer, Richard Powell, G. V. D. Driessche, Lisa Anne Hendricks, Maribeth Rauh, Po-Sen Huang, Amelia Glaese, Johannes Welbl, Sumanth Dathathri, Saffron Huang, Jonathan Uesato, John F. J. Mellor, I. Higgins, Antonia Creswell, Nathan McAleese, Amy Wu, Erich Elsen, Siddhant M. Jayakumar, Elena Buchatskaya, D. Budden, Esme Sutherland, K. Simonyan, Michela Paganini, L. Sifre, Lena Martens, Xiang Lorraine Li, A. Kuncoro, Aida Nematzadeh, E. Gribovskaya, Domenic Donato, Angeliki Lazaridou, A. Mensch, J. Lespiau, Maria Tsimpoukelli, N. Grigorev, Doug Fritz, Thibault Sottiaux, Mantas Pajarskas, Tobias Pohlen, Zhitao Gong, Daniel Toyama, Cyprien de Masson d’Autume, Yujia Li, Tayfun Terzi, Vladimir Mikulik, I. Babuschkin, Aidan Clark, Diego de Las Casas, Aurelia Guy, Chris Jones, James Bradbury, Matthew Johnson, Blake A. Hechtman, Laura Weidinger, Iason Gabriel, William S. Isaac, Edward Lockhart, Simon Osindero, Laura Rimell, Chris Dyer, Oriol Vinyals, Kareem W. Ayoub, Jeff Stanway, L. Bennett, D. Hassabis, K. Kavukcuoglu, Geoffrey Irving. 2021. Introduces Gopher from DeepMind.
- Jurassic-1: Technical details and evaluation. Opher Lieber, Or Sharir, Barak Lenz, Yoav Shoham. 2021. Introduces Jurassic from AI21 Labs.
Encoder-only 架构:
- BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. Jacob Devlin, Ming-Wei Chang, Kenton Lee, Kristina Toutanova. NAACL 2019. Introduces BERT from Google.
- RoBERTa: A Robustly Optimized BERT Pretraining Approach. Yinhan Liu, Myle Ott, Naman Goyal, Jingfei Du, Mandar Joshi, Danqi Chen, Omer Levy, M. Lewis, Luke Zettlemoyer, Veselin Stoyanov. 2019. Introduces RoBERTa from Facebook.
Encoder-decoder 架构:
- BART: Denoising Sequence-to-Sequence Pre-training for Natural Language Generation, Translation, and Comprehension. M. Lewis, Yinhan Liu, Naman Goyal, Marjan Ghazvininejad, Abdelrahman Mohamed, Omer Levy, Veselin Stoyanov, Luke Zettlemoyer. ACL 2019. Introduces BART from Facebook.
- Exploring the Limits of Transfer Learning with a Unified Text-to-Text Transformer. Colin Raffel, Noam M. Shazeer, Adam Roberts, Katherine Lee, Sharan Narang, Michael Matena, Yanqi Zhou, W. Li, Peter J. Liu. J. Mach. Learn. Res. 2019. Introduces T5 from Google.