一、实验目的
掌握趋势外推预测模型的基本理论,通过编程对实例进行预测。
二、实验任务
在佩尔预测模型、龚珀兹预测模型和林德诺预测模型中任选其一,进行编程预测。
本实验选择:佩尔预测模型
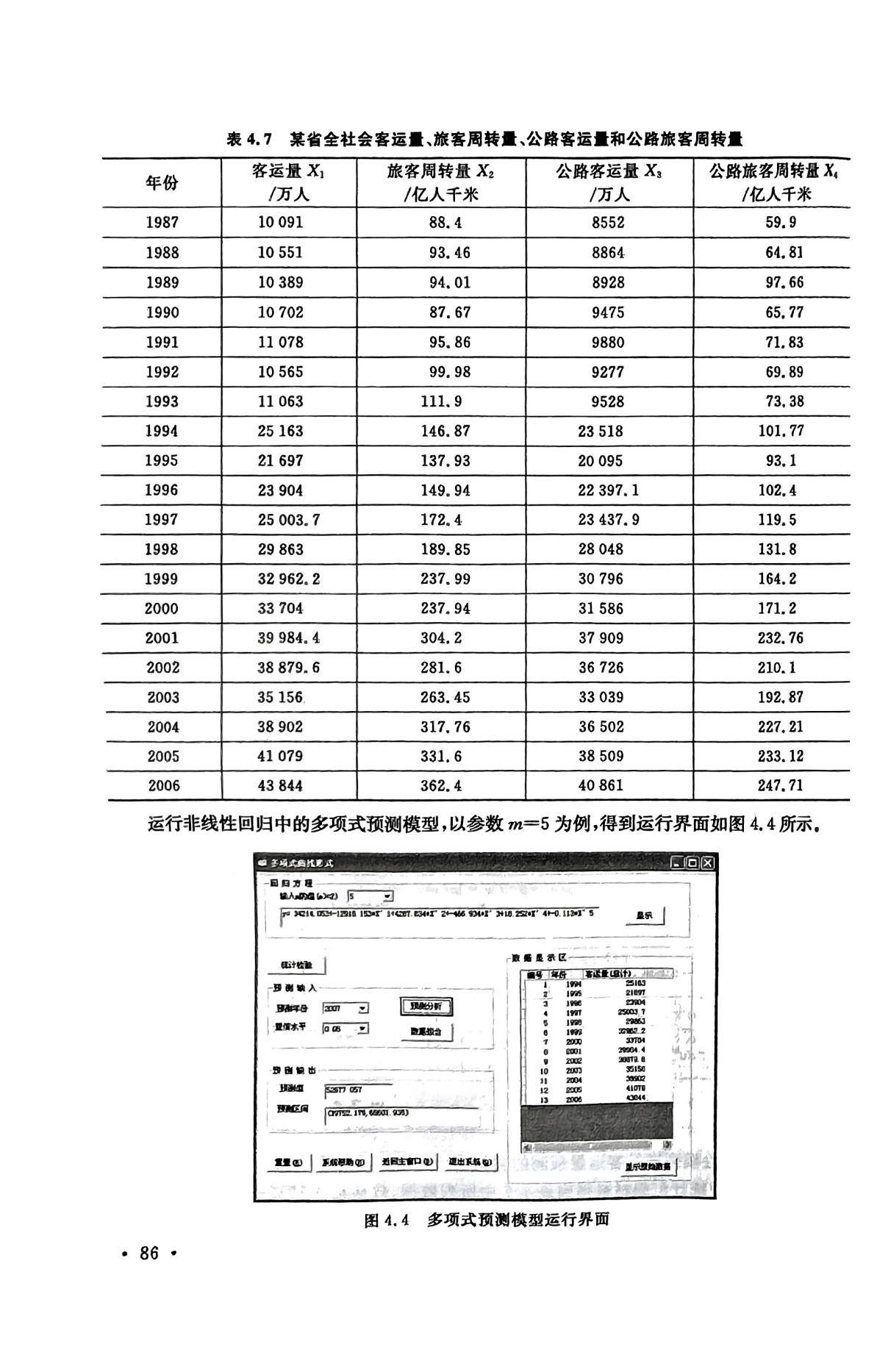
数据实例如下:
三、实验过程
四、实验结果
实现平台:Matlab 2022A
实验代码:
% 年份和客运量的数据
% years = 1987:2006;
% passengers = [10091,10551,10389,10702,11078,10565,11063,25163,21697,23904,25003.7,29863,32962.2,33704,39984.4,38879.6,35156,38902,41079,43844];
years = 1994:2006;
passengers = [25163,21697,23904,25003.7,29863,32962.2,33704,39984.4,38879.6,35156,38902,41079,43844];
% 求解参数
% 计算数组的长度
n = length(years);
% 将数组分为三份
r = floor(n / 3);
part1 = passengers(1:r);
part2 = passengers((r + 1):(2 * r));
part3 = passengers((2 * r + 1):end);
% 求每份的总和
S1 = sum(1 ./ part1);
S2 = sum(1 ./ part2);
S3 = sum(1 ./ part3);
% 求各个参数
b = log((S1 - S2) / (S2 - S3)) / r;
L = r / (S1 - ((S1 - S2)^2 / ((S1 - S2) - (S2 - S3))));
a = ((S1 - S2)^2 * (1 - exp(-b)) * L) / (((S1 - S2) - (S2 - S3)) * exp(-b) * (1 - exp(-r * b)));
% 输出参数值
disp(['参数 L 的值为: ', num2str(L)]);
disp(['参数 a 的值为: ', num2str(a)]);
disp(['参数 b 的值为: ', num2str(b)]);
% 应用模型进行预测
t = 1:length(years);
predicted_passengers = L ./ (1 + a * exp(-b * t));
% 可视化预测结果
figure;
plot(years, passengers, '-', 'DisplayName', '实际乘客数量');
hold on;
plot(years, predicted_passengers, '-', 'LineWidth', 2, 'DisplayName', '预测乘客数量');
xlabel('年份');
ylabel('乘客数量');
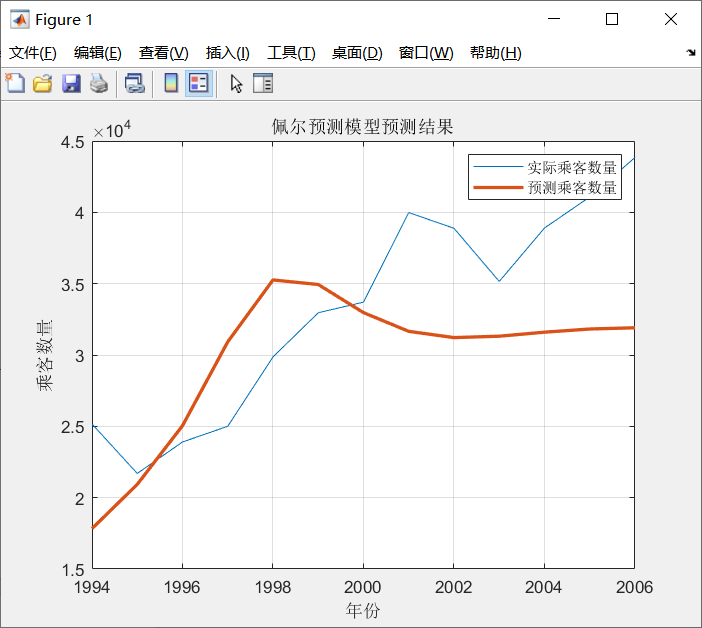
title('佩尔预测模型预测结果');
legend;
grid on;
实验结果:
五、个人总结
1.对趋势外推预测模型的理解
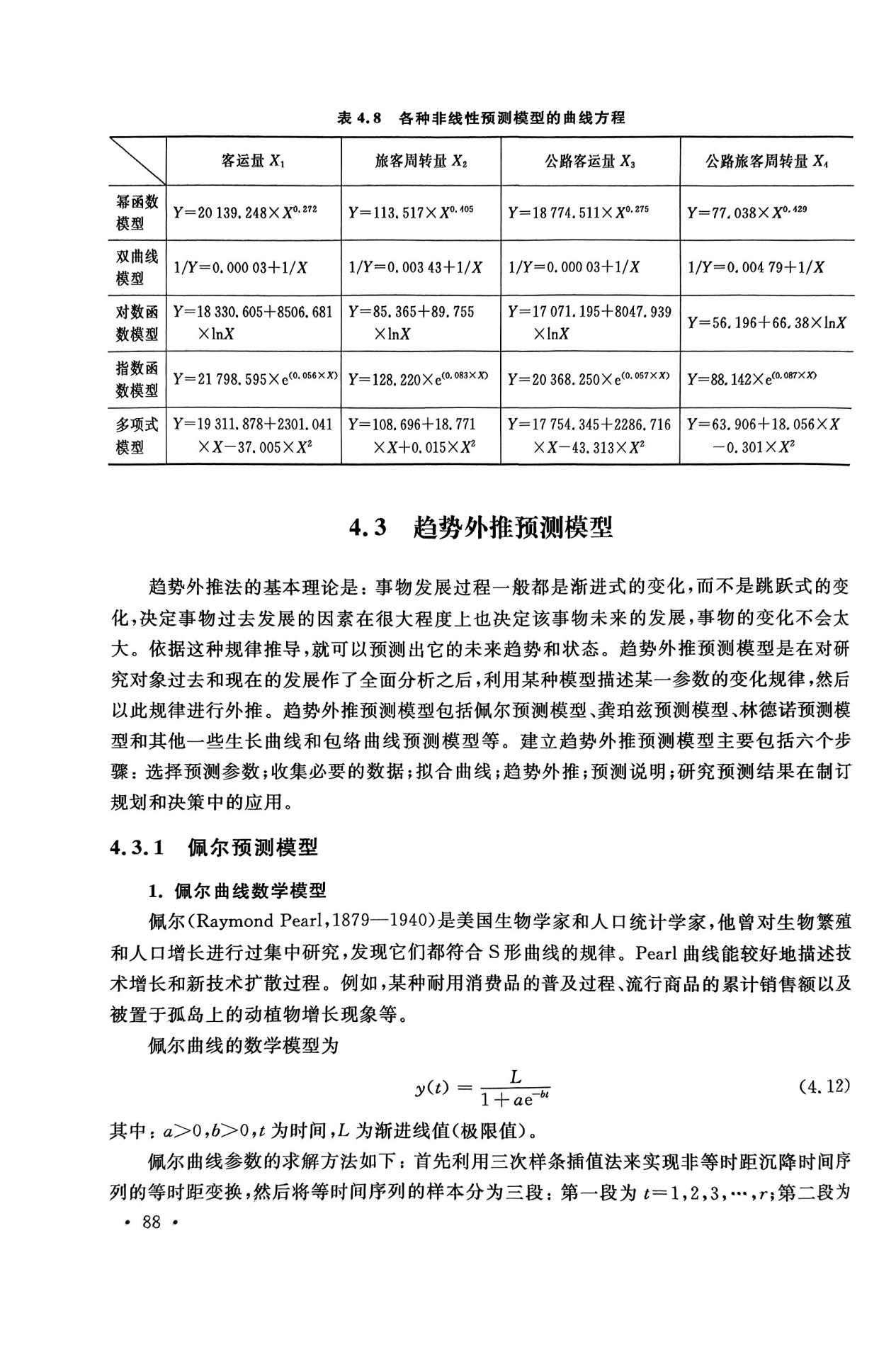
趋势外推法的基本理论是:事物发展过程一般都是渐进式的变化,而不是跳跃式的变化,决定事物过去发展的因素在很大程度上也决定该事物未来的发展,事物的变化不会太大。依据这种规律推导,就可以预测出它的未来趋势和状态。
本次实验采用的佩尔模型是从生物繁殖和人口增长的S型曲线规律当中分析而出,能够较好地描述技术增长和新技术扩散过程。