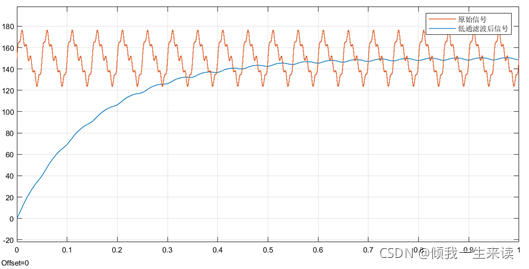
一阶低通滤波
低通滤波(Low-pass filter) 是一种过滤方式,规则为低频信号能正常通过,而超过设定临界值的高频信号则被阻隔、减弱,一阶低通滤波的传递函数如下所示。
G
(
s
)
=
ω
c
/
(
s
+
ω
c
)
G(s)=ω_c/(s+ω_c )
G(s)=ωc/(s+ωc)
ω
c
ω_c
ωc为滤波截止角频率,实际应用中经常令
T
=
1
/
ω
c
T=1/ω_c
T=1/ωc,一阶低通滤波器传递函数可改写为:
G
(
s
)
=
1
/
(
T
s
+
1
)
G(s)=1/(Ts+1)
G(s)=1/(Ts+1)
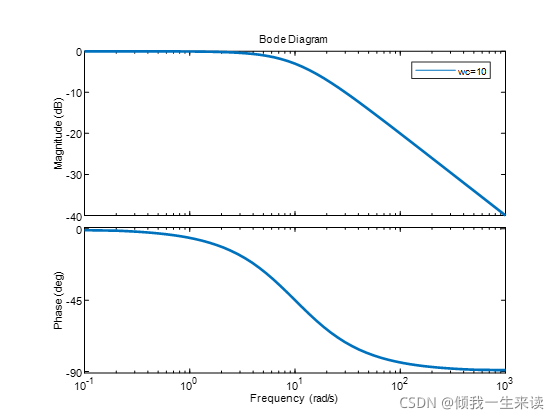
其中T是滤波时间常数,s为拉普拉斯的算子,一阶低通滤波器的伯德图如下所示。
横坐标为,输出与输入之比再取对数。对低通滤波器进行离散化,使用后向差分变换,变换公式为:
s
=
(
1
−
z
−
1
)
/
T
s
s=(1-z^-1 )/T_s
s=(1−z−1)/Ts
将变化公式带入传递函数,可得差分方程:
y
(
n
)
=
(
ω
c
T
s
)
/
(
1
+
ω
c
T
s
)
x
(
n
)
+
1
/
(
1
+
ω
c
T
s
)
y
(
n
−
1
)
y(n)=(ω_c T_s)/(1+ω_c T_s ) x(n)+1/(1+ω_c T_s ) y(n-1)
y(n)=(ωcTs)/(1+ωcTs)x(n)+1/(1+ωcTs)y(n−1)
令
a
=
(
ω
c
T
s
)
/
(
1
+
ω
c
T
s
)
a=(ω_c T_s)/(1+ω_c T_s )
a=(ωcTs)/(1+ωcTs),则
1
/
(
1
+
ω
c
T
s
)
=
1
−
a
1/(1+ω_c T_s )=1-a
1/(1+ωcTs)=1−a,整理后得到低通滤波器的差分方程为:
y
(
n
)
=
a
x
(
n
)
+
(
1
−
a
)
y
(
n
−
1
)
y(n)=ax(n)+(1-a)y(n-1)
y(n)=ax(n)+(1−a)y(n−1)
其中:y(n)为本次滤波值,y(n-1)上次滤波值为, x(n)为本次采样值。
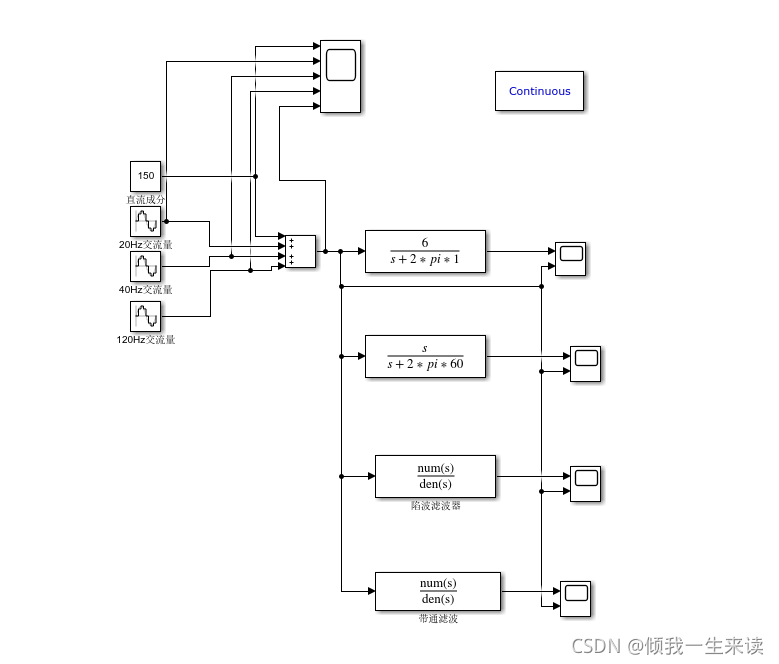
仿真模型
simulink仿真模型
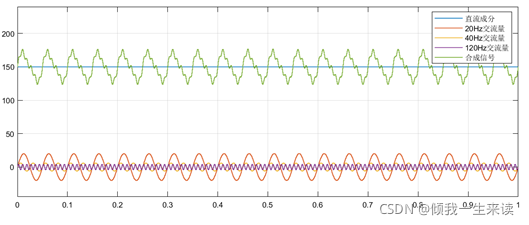
测试信号合成
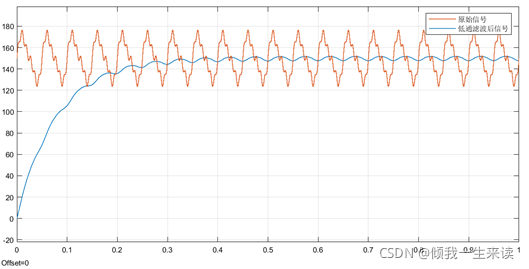
低通滤波截止频率2Hz
低通滤波截止频率1Hz