题目描述:
给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是 回文串 。返回 s 所有可能的分割方案。
回文串 是正着读和反着读都一样的字符串。
示例 1:
输入:s = “aab”
输出:[[“a”,“a”,“b”],[“aa”,“b”]]
示例 2:
输入:s = “a”
输出:[[“a”]]
思路分析:
这道题题意是找所有的分割方法。这个题意一定要搞清楚,意思就是所给的S字符串里可以切任意刀,列如aab字符串,切割方法其实非常多,比如a|ab,aa|b,a|a|b, 这里就是要返回所有切割后子串为回文的组合。实际上跟之前组合的题挺像的,之前的条件是找所有组合等于某个值,现在的条件是组合为回文。
一开始我想着用滑动窗口做,后来发现,不太行,太复杂了 要考虑的情况非常多。
还是老老实实回溯吧。
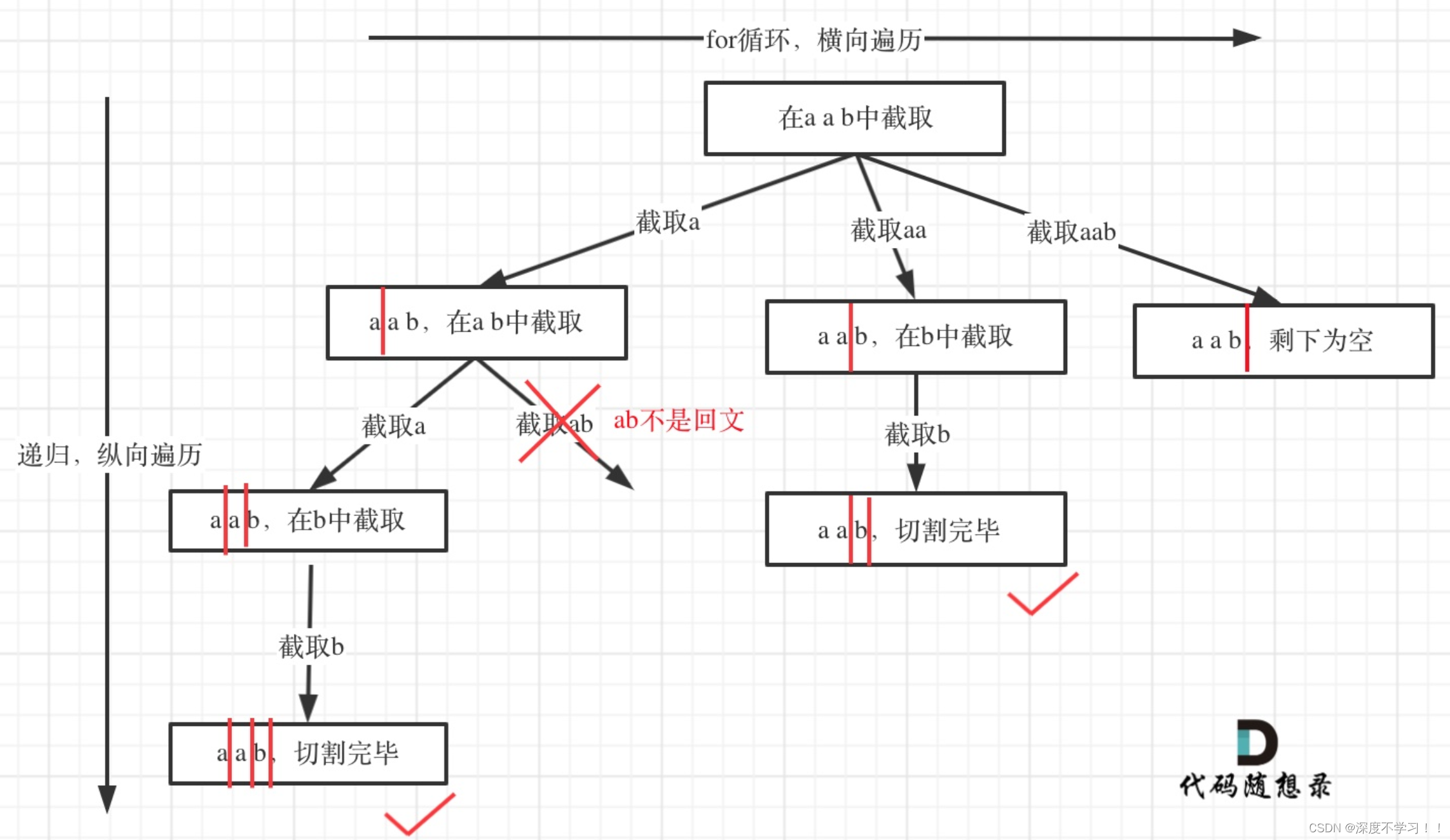
先上我偷的图,方便理解。
老规矩 回溯三步走:
1.确定函数参数:
这个题的参数比较好确定,一个是记录路径上元素的列表path,另一个就是回溯中常用的startindex了,这个参数就不多说了,之前的文章里说了N边啦。
2.确定终止条件
看上面我偷的那个图,里面的 ‘|’ 表示分割,显然,当 分割符到字符串末尾的时候,表示分割完了,也就是到叶子节点了。
在之前的回溯中已经比较套路化了,for里的i变量控制横向,startindex控制纵向告诉下一层横向的i从哪里开始,所以实际上这里的startindex就是切割点。(当切割点到最后了,也就是startindex到最后了,代表着结束)
所以终止条件就是 当 startindex == len(s)时,表示遍历到最后了,将path记录的字符串加入到结果集。
二刷补充:在回溯的参数传递上本来是i+1,写成startindex+1了。
原因:
这里通俗的理解就是,startindex控制的是每一层的起始值,i从startindex遍历到字符串末尾,也就是i控制的是当前这一层的每一个分支,当递归往下层走的时候,传递的应该是i+1,当前层遍历到第i个分支了,则当前层第i个分支的下面分支从i+1开始。所以i+1就当做了下面分支的起始值startindex。
3.回溯循环体:
首先要确定当前判断的是那一个子字符串,从开始的下标startindex到当前遍历的下标i。也就是判断s[startindex:i+1]是不是回文的,是就将当前子字符串加入到路径集合path,如果不是则不判断当前分支了。因为是要截取子字符串,当其中一个不是回文,这个分支就可以扔了。 比如|A|AB| 这里的AB已经不是回文了,再往下也没意义了。(题意就是这样,其中一个切割出来的子串不是回文,就pass)
完整代码:
class Solution:
def partition(self, s: str) -> List[List[str]]:
res = []
path = []
def backtrack(path,startindex):
# 确定终止条件
# 当切割线切割到最后一位的时候表示到了叶子节点
# startindex相当于切割线
if startindex == len(s):
res.append(path[:])
# 回溯体
for i in range(startindex,len(s)):
# 截取当前的字串判断是否回文
temp = s[startindex:i+1]
if temp == temp[::-1]:
path.append(s[startindex:i+1])
else:
continue # 但判断不是回文的时候,再继续本分支已经没有意义了,因为是要截取子字符串,当其中一个不是回文,这个分支就可以扔了。 比如\A\AB\ 这里的AB已经不是回文了,再往下也没意义了.
backtrack(path,i+1)
path.pop()
backtrack(path,0)
return res