【信息学奥赛】CSP-J/S初赛05 计算机原码、补码和反码

本专栏👉CSP-J/S初赛内容主要讲解信息学奥赛的初赛内容，包含计算机基础、初赛常考的C++程序和算法以及数据结构，并收集了近年真题以作参考。

如果你想参加信息学奥赛，但之前没有太多C++基础，请点击👉专栏：C++语法入门，如果你C++语法基础已经炉火纯青，则可以进阶算法👉专栏：算法知识和数据结构👉专栏：数据结构啦

📕带符号二进制数的表示方法

🧠原码表示法

🧠反码表示法

🧠补码表示法

📕定点数和浮点数

♥定点数(Fixed-Point Number)

♥浮点数(Floating-Point Number)

带符号二进制数的表示方法

带符号二进制数用最高位的一位数来表示符号：0表示正，1表示负。

带符号位二进制数位数	数值范围	十六进制范围表示法
8位二进制数	-128 ~ +127	80H~7FH
16位二进制数	-32768 ~ +32767	8000H~7FFFH
32位二进制数	-2147483648 ~+2147483647	80000000H~7FFFFFFFH

注：符号位的表示：最常用的表示方法有原码、反码和补码。

原码表示法

一个机器数x由符号位和有效数值两部分组成，设符号位为x0，x真值的绝对值|x|=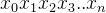 $x_{0}x_{1}x_{2}x_{3}..x_{n}$ ，则 x的机器数原码可表示为：

[x]原= 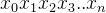$x_{0}x_{1}x_{2}x_{3}..x_{n}$ ，当 x>=0时， $x_{0}$ =0，当x<0时， $x_{0}$ =1。

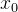
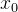
例如：已知x1=-1011B，x2= +1001B，则 x1，x2有原码分别是

[x1]原=11011B，[x2]原=01001B

规律：正数的原码是它本身，负数的原码是取绝对值后，在最高位（左端）补“1”。

反码表示法

一个负数的原码符号位不变，其余各位按位取反就是机器数的反码表示法。

正数的反码与原码相同。

按位取反的意思是该位上是1的，就变成0，该位上是0的就变成 1。即 1=0，0=1

例：x1 = −1011B，x2 = +1001B ，求[x1]反和[x2]反

解：[x1]反=10100B，[x2]反 =01001B

补码表示法

首先分析两个十进制数的运算：79-38=41，79+62=141

如果使用两位数的运算器，做79+62时，多余的100因为超出了运算器两位数的范围而

自动丢弃，这样在做79-38的减法时，用79+62的加法同样可以得到正确结果。

模是指一个计量系统的测量范围，其大小以计量进位制的基数为底数，位数为指数的幂。

如两位十进制数的测量范围是 1—99，溢出量是100，模就是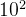 $10^{2}$ =100，上述运算称为模运算，可以写作：79+(-38)=79+62(mod 100)

进一步写为-38=62，此时就说–38的补法（对模 100而言）是 62。计算机是一种有限

字长的数字系统，因此它的运算都是有模运算，超出模的运算结果都将溢出。n位二进制的

模是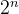 $2^{n}$ 。

当x>=0时，补码就是其本身。例如[+1]=[00000001]原=[00000001]反=[00000001]补
当x<0时，在其原码的基础上，符号位不变，其余各位取反，最后再+1（即在反码的基础上+1）。例如[-1]=[10000001]原=[11111110]反=[11111111]补

定点数和浮点数

定点数(Fixed-Point Number)

计算机处理的数据不仅有符号，而且大量的数据带有小数，小数点不占有二进制一位而是隐含在机器数里某个固定位置上。通常采取两种简单的约定：一种是约定所有机器数的小数的小数点位置隐含在机器数的最低位之后，叫定点纯整机器数，简称定点整数。另一种约定所有机器数的小数点隐含在符号位之后、有效部分最高位之前，叫定点纯小数机器数，简称定点小数。无论是定点整数，还是定点小数，都可以有原码、反码和补码三种形式。

浮点数(Floating-Point Number)

计算机多数情况下采作浮点数表示数值，它与科学计数法相似，把一个二进制数通过移动小数点位置表示成阶码和尾数两部分：N = 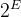$2^{E}$ * S

其中：E--N的阶码(Expoent),是有符号的整数。

S--N的尾数(Mantissa),是数值的有效数字部分，一般规定取二进制定点纯小数形式。

例如：1011101B= $2^{+7}$ *0.1011101，101.1101B= $2^{+3}$ *0.1011101，0.01011101B= $2^{-1}$ *0.1011101