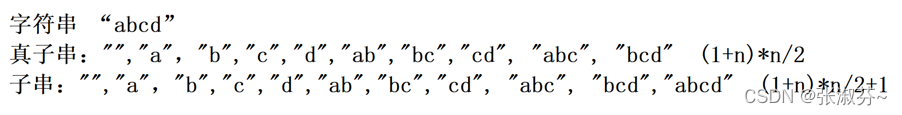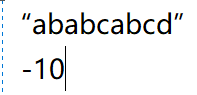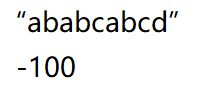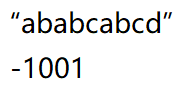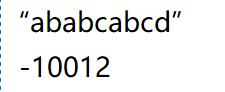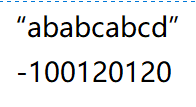在字符串匹配的时候，我们经常用到BF算法和KMP算法。

首先一张图了解子串和真子串：

子串比真子串多了一个字符串本身。

比如我们在主串"ababcabcdabcde"中找到子串"abcd",从头开始查找返回的下标为5，从下标7号位置查找则返回下标9.

BF算法：

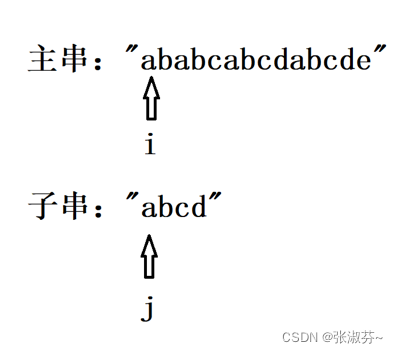
首先我们需要定义两个整形值 i 和 j ，分别指向两个字符串的0号下标位置。

如果 i 和 j 指向的字符相同，则 i++, j++。

如果 i 和 j 指向的字符不相同，则，i=i-j+1,j=0;(i指向上一次开始位置的下一个位置)

退出条件： i 或 j 走出自身范围（越界）

退出之后，我们需要判断是否找到，只选要看 j 即可，j 走出自身范围，找到了，返回 i - j , j 没有走出自身范围，没有找到，我们返回一个负数，代表错误，这里返回-1.

 BF算法代码：

int BF(const char* str,const char*sub,int pos)//pos->主串开始向后搜索的开始位置，光标
{
	assert(str != NULL && sub != NULL && pos >= 0 && pos < strlen(str));
	int i = pos, j = 0;
	int len_str = strlen(str);
	int len_sub = strlen(sub);
	while (i < len_str && j < len_sub)
	{
		if (str[i] == sub[j])
		{
			i++;
			j++;
		}
		else
		{
			//i和j顺序不能颠倒
			i = i - j + 1;//回退到这一趟开始位置的下一个位置
			j = 0;
		}
	}
	if (j < len_sub)
	{
		return -1;
	}
	else
	{
		return i - j;
	}
}

BF算法优缺点：

优点：逻辑简单，实现也简单

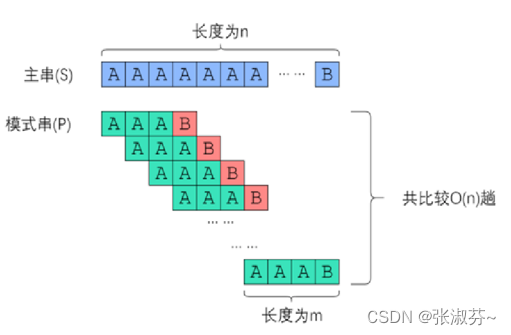
缺点：效率很低，时间复杂度O(n*m)类似于n^2

KMP算法：

这里的KMP算法理解起来有点难。

KMP算法的核心思想， i 打死不回退。

 按照BF算法，我们发现在下标为3的地方发生失配（不匹配），此时j=0,i=1,也发生了失配；j=0，i=2，又发生了失配；j=0,i=3，这是才可以正常比较。什么意思，我们会发现中间的那两次一定会失败，压根没有必要在去执行。

再举一个例子：

 方框框中的是没有必要去跑的，此时j=5，指向最后一个字符，因为i打死不能回退，此时i=5,我们需要一种方法，让 j 不在等于0，而是等于2，（因为i指向的前两位和j指向的前两位相同）此时，只需要判断 i 和 j 指向的字符是否相等，相等，i++,j++，不相等，则继续让j换指向，这里发现子串就没有d ，所以不可能找到相匹配的，那么怎么用代码实现呢？

我们需要对子串每一个字符有一个对应数字，这个数字干什么用的呢？

当我们子串和主串发生失配时，由于i不能动，只能动 j，一旦发生失配，这里j指向的字符所对应的数字就是我们需要j下一次比较所指向的下标。

看不懂没关系，继续向下看。

先说怎么给子串每一个字符有一个对应的数字：

1.子串的0号下标和1号下标对用的数字固定为-1,0.（这里的子串为"ababcabcd"）

 从j=1的位置（即b）开始，看b对应的数字的下标位置对应的字符（即a）和自身（b）相不相同，相同，自身对应的下标加1，放在下一个位置上，不相同，则自身对应的数字（0）的下标位置所对应的字符（a）对应的数字（即-1）加1放在自身的下一个位置，这几句话慢慢理解。这里由于b和a不相同，所以-1+1=0，放在b的下一个位置。

 继续,此时j=2，a对应的数字（0）的下标位置对应的字符（a）和自身（a）相同，则a对应的下标数字+1,0+1=1,放在下一个位置。

此时j=3,b对应的数字（1）的下标位置对应的字符（b）和自身（b）相同，则b对应的下标数字+1,1+1=2，放在下一个位置。

 这里还需注意，我们看c对应的数字（2）的下标位置对应的字符（a）和自身（c）不相同，我们发现不相同，此时我们还需要判断c和下标2位置对应的字符a所对应的数字（0）的下标位置对应的字符（a）和自身（c）相不相同，发现不相同，则这里是-1+1=0放在下一个位置。也就是说发现不相同看和自身比较字符是不是下标为0的那个字符，不是，则继续和刚才和自身比较的字符对应的数字的下标位置所对应的字符继续比较。

依次类推，得到

这样就得到了子串每个字符所对应的数字。

 在来看代码：

int* Get_Next(const char* sub)//求子串的模式匹配串next
{
	assert(sub != NULL);
	int len = strlen(sub);
	
	int* next = (int*)malloc(sizeof(int) * len);//存放对应的数字
	assert(next != NULL);
	next[0] = -1;
	next[1] = 0;

	int j = 1;//通过已知推未知
	int k = next[1];
	while (j + 1 < len)
	{
		if (k==-1||sub[j] == sub[k])
		{
			k++;
			j++;
			next[j] = k;
		}
		else
		{
			k = next[k];//这里是最难看懂的地方，可以自己写一个案例，再通过代码来实现去理解
		}
	}
	return next;
}
//这里的代码和BF算法差不多，只不过不相同时代码变了
int KMP(const char* str, const char* sub,int pos)
{
	assert(str != NULL && sub != NULL && pos >= 0 && pos < strlen(str));
	int i = pos, j = 0;
	int len_str = strlen(str);
	int len_sub = strlen(sub);
	
	int* next = Get_Next(sub);
	while (i < len_str && j < len_sub)
	{
		if (j==-1||str[i] == sub[j])
		{
			i++;
			j++;
		}
		else
		{
			
			j = next[j];
		}
	}
	free(next);
	
	if (j < len_sub)
	{
		return -1;
	}
	else
	{
		return i - j;
	}
}