问题描述
八皇后问题,是一个古老而著名的问题,是回溯算法的典型案例。该问题是国际西洋棋棋手马克斯·贝瑟尔于1848年提出:在8×8格的国际象棋上摆放八个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,八皇后问题可以推广为更一般的n皇后摆放问题:这时棋盘的大小变为n×n,而皇后个数也变成n。当且仅当n = 1 或 n ≥ 4 时问题有解。
要求对于给定一个整数 n,返回所有不同的 n 皇后问题的解决方案。
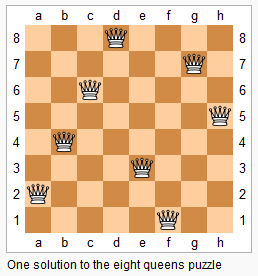
下图为8皇后的其中一种放置方法
http://www.brainmetrix.com/8-queens/
这个链接可以操作摆放皇后位置,能更好的理解n皇后问题
回溯法: 采用试错的思想,它尝试分步的去解决一个问题。在分步解决问题的过程中,当它通过尝试发现现有的分步答案不能得到有效的正确的解答的时候,它将取消上一步甚至是上几步的计算,再通过其它的可能的分步解答再次尝试寻找问题的答案。简单来说就是:先选择一条路走到黑,走不动了退回来一步,再探索其他的方向。
回溯和递归的区别
递归:为了描述问题的某一状态,必须用到该状态的上一状态,而描述上一状态,又必须用到上一状态的上一状态……这种用自已来定义自己的方法,称为递归定义。例如斐波拉契数列的f(n){if(n <= 2) return 1; f(n) = f(n-1)+f(n-2);}
回溯:从问题的某一种可能出发,搜索从这种情况出发所能达到的所有可能, 当这一条路走到 “尽头” 的时候, 再退回上一步,从另一种可能出发,继续搜索。 这种不断 “回溯” 寻找解的方法,称作 “回溯法”。 简单来说,回溯是一种算法思想,可以用递归实现。
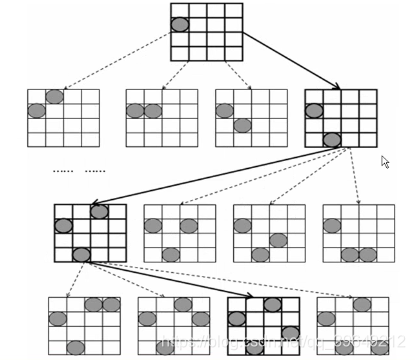
回溯过程:
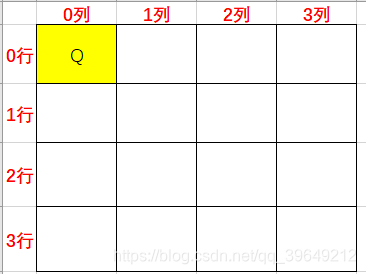
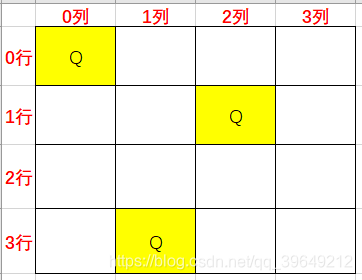
为了便于理解,缩小问题规模,以下图4皇后为例,采取按列由左至右的放置方法,首先0列0行放置一个皇后。
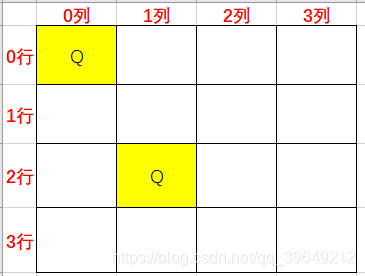
接着选1列2行放置。
接着轮到放置2列的时候发现0,1,2,3行都不能放了,说明1列放置的不对,所以我们要回溯到1列,发现1列还有第3行可以放置,因此我们选择3行来放置,放置后2列的1行也可以放置了,如下图所示。
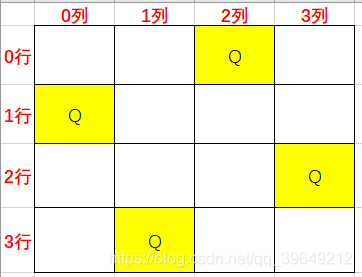
放置最后一列时,都不能放了,说明2列放置的不对,但2列也没有其他位置可以选择,因此1列放置的不对,1列也没有其他选择,因此0列放置的也不对,所以我们回溯到了0列,选择0列1行开始放置,再重复上面的步骤,直到找到正确的放置方案。下图就是4皇后的一个正确方案。
解题思路:
用经典的深度递归回溯解法,大概的思路就是对每一列,每一行去放置,如果能走到最后一列并且放置了皇后,就保存结果输出,没位置放了,就回溯到上一列。
难点大概就是使用一维数组保存每列皇后所在的行,例如int[] cols = [1,3,0,2],它代表0列皇后放在第1行,1列放在3行,2列放在0行,3列放在2行,如上图所示。
在放置每一列的过程中,再使用一个布尔数组boolean [] rows,用它来约束放置的位置。还是以上图为例,假设我们放置完了0列和1列,到了2列的时候boolean [] rows应该为[false,true,true,true],因为数组默认值都为false,所以我们默认false为可以放置,true为不能放置,根据数组中的值可知2列皇后只能放置在0行的位置。
那么如何约束皇后放置的位置呢?
如果把棋盘看成平面直角坐标系,假设一个已放置的皇后的位置为(x1,y1),即将要放置的皇后位置为(x2,y2),则行、正斜、反斜的限制关系可以表示为:
y2!=y1 (限制同一行),
y2!=y1-(x2-x1) (限制正斜方向(/)),
y2!=y1+(x2-x1) (限制反斜方向(\)),
其中
y2!=y1 可以用数