EK算法流程

EK算法的流程很简单：

1. 随意找一个可行流作为流量网络更新的基础（一般题目没有规定可以采用流量为0的可行流）
2. 利用$bfs$找一条从源点到汇点的可行流路径
3. 用新找到的可行流路径更新原有流量网络：先找到该可行流路径中流量最小边，然后将该路径上所有正向边都减去该最小边的流量，反向边都加上该最小边的流量（想想，为什么要设反向边）
4. 不断重复2和3两个步骤，直到在第2步的时候找不到一条从源点到汇点的可行流路径（已经达到最大流的流量网络满足的特征是，源点能达到的所有点记作集合s，不能达到的所有点记作集合t，那么从s到t的所有边流量都为0，t到s的所有边的流量之和即为最大流）

反向边的作用

反向边的作用，用一个词概括：后悔药
如果没有反向边，那么我们随意找到一个可行流，例如这个：

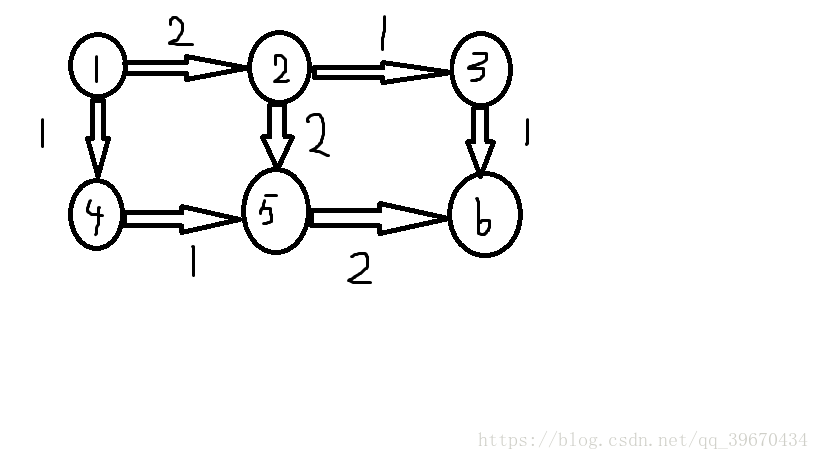
我们很容易找到一个可行流：1->2->5->6，流量为2。
到这一步之后我们发现我们无法再进行增广。

如果这时候我们添加了反向边，就会是这样：

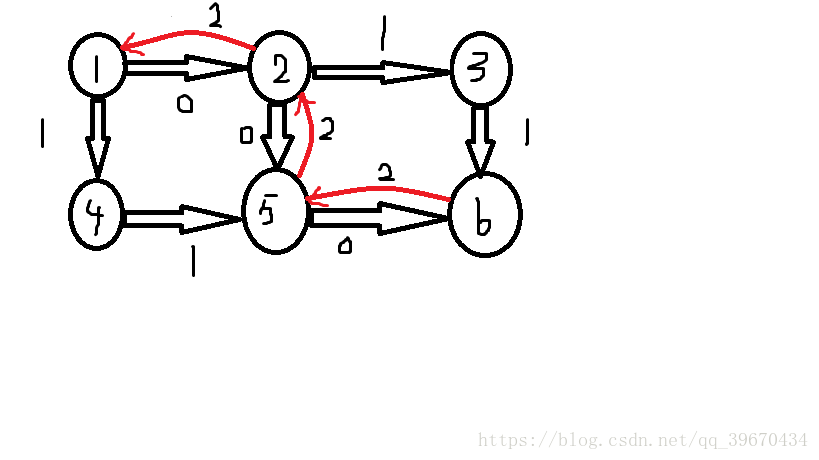
那么通过反向边，我们可以又找到这么一条可行流路径：1->4->5->2->3->6，流量为1.
所以最后的最大流是3。
有了反向边，我们可以做到这件事情：如果我们发现某一条边上分配流量过多，不利于最优方案的推出，我们利用反向边可以反悔。
所以反向边增大的意义就在于正向边的流量减小，也就是“退流”。
所以我们可以发现，始终满足：正向边流量+反向边流量=该边容量

代码实现

#include<bits/stdc++.h>
using namespace std;
inline int read(){
    int num=0;char c=' ';bool flag=true;
    for(;c>'9'||c<'0';c=getchar())
        if(c=='-')
            flag=false;
    for(;c>='0'&&c<='9';num=(num<<3)+(num<<1)+c-48,c=getchar());
    return flag ? num : -num;
}
const int maxn=10020;
const int maxm=100020;
const int INF=1e8;
namespace Graph{
    int n,m,s,t;
    int top=0,head[maxn];
    struct node{
        int dot,val,next;
    }a[maxm<<1];//邻接表  
    void insert(int x,int y,int w){
        a[top].dot=y;
        a[top].val=w;
        a[top].next=head[x];
        head[x]=top++;
    }//插入边 
    void init(){
        n=read();m=read();//点数、边数 
        s=read();t=read();//源点、汇点 
        memset(head,-1,sizeof head);
        for(int i=1;i<=m;i++){
            int x=read(),y=read(),v=read();
            insert(x,y,v);
            insert(y,x,0);//插入反向边为
        }
    }
}using namespace Graph;

namespace Flow{
    struct flow{
        int edge,v;
    }pre[maxn];
    //记录了某点在某一条可行流中 
    //它的前驱点和连接它和它的前驱的有向边的编号 
    bool vis[maxn];//是否被访问过 
    bool bfs(){
        queue<int>q;
        memset(vis,0,sizeof vis);
        memset(pre,-1,sizeof pre);//初始化 
        q.push(s);
        vis[s]=true;
        pre[s].v=s;
        while(!q.empty()){
            int u=q.front();
            q.pop();
            for(int i=head[u];i!=-1;i=a[i].next){
                int v=a[i].dot;
                if(!vis[v]&&a[i].val){
                //如果该边的流量不为0或者没有访问过
                    pre[v].v=u;
                    pre[v].edge=i;//记录前驱和边 
                    vis[v]=true;//标记访问过 
                    if(v==t)return true;
                    //如果到汇点了，那么这个可行流路径算是找到了 
                    q.push(v);
                }
            }
        }
        return false;//找不到 
    }
    void EK(){
        int ans=0;
        while(bfs()){//当可以找到的时候
            int flow=INF;
            for(int i=t;i!=s;i=pre[i].v){
                flow=min(flow,a[pre[i].edge].val);
            }//找到最小流量 
            ans+=flow;//本次增广收益哈哈哈 
            for(int i=t;i!=s;i=pre[i].v){
                int edge=pre[i].edge;
                a[edge].val-=flow;//正向边表示的是残余网络 
                a[edge^1].val+=flow;//反向边表示的是流量
                //始终保持和相加等于容量 
            }
        }
        printf("%d\n",ans);
    }
}using namespace Flow;
int main(){
    init();
    EK();
    return 0;
}

时间复杂度

时间复杂度$O(n\times m^2)$但是，一般不会更新那么多次。
一般能处理$10^3$到$10^4$规模的网络。