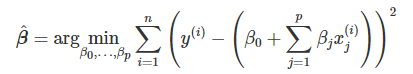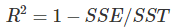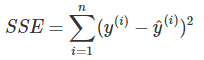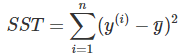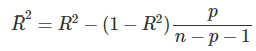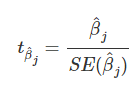Interpretable Machine Learning线性回归
线性回归模型将目标预测为特征输入的加权和。学习关系的线性使解释变得容易。线性回归模型长期以来被统计学家,计算机科学家和其他解决定量问题的人所使用。
线性模型可用于模拟回归目标y对某些特征x的依赖性。学习的关系是线性的,可以为单个实例i编写,如下所示:
ϵ是我们仍然犯的错误,即预测和实际结果之间的差异。假设这些误差遵循高斯分布,这意味着我们在负方向和正方向上都产生误差并且产生许多小误差和很少的大误差。
可以使用各种方法来估计最佳重量。普通最小二乘法通常用于找到最小化实际和估计结果之间的平方差异的权重:
线性回归模型的最大优点是线性:它使估计过程简单,最重要的是,这些线性方程在模块级别(即权重)上具有易于理解的解释。这是线性模型和所有类似模型在医学,社会学,心理学和许多其他定量研究领域等学术领域如此普遍的主要原因之一。例如,在医学领域,不仅重要的是预测患者的临床结果,而且还要量化药物的影响,同时以可解释的方式考虑性别,年龄和其他特征。
估计的权重带有置信区间。置信区间是权重估计的范围,其以一定的置信度覆盖“真实”权重。例如,权重为2的95%置信区间可以在1到3之间。此区间的解释将是:如果我们使用新采样数据重复估计100次,则置信区间将包括95中的真实权重。在100个案例中,假设线性回归模型是数据的正确模型。
模型是否是“正确”模型取决于数据中的关系是否满足某些假设,即线性,正态性,同方差性,独立性,固定特征以及缺乏多重共线性。
线性
线性回归模型迫使预测成为特征的线性组合,这是其最大强度和最大限制。线性导致可解释的模型。线性效应易于量化和描述。它们是添加剂,因此很容易分离效果。如果您怀疑要素交互或要素与目标值的非线性关联,则可以添加交互项或使用回归样条线。
常态
假设给定特征的目标结果遵循正态分布。如果违反该假设,则特征权重的估计置信区间无效。
同调性(恒定方差)
假设误差项的方差在整个特征空间上是恒定的。假设您想以平方米为单位预测房屋的价值。您估计一个线性模型,假设无论房屋的大小如何,预测响应周围的误差都具有相同的方差。这种假设在现实中经常被违反。在房子的例子中,大型房屋的预测价格周围的误差项的方差可能更高,因为价格更高且价格波动的空间更大。假设线性回归模型的平均误差(预测价格与实际价格之间的差异)为50,000欧元。如果你假设同方差性,你会认为对于花费100万的房屋和仅花费40,000的房屋,平均误差为50,000是相同的。这是不合理的,因为这意味着我们可以预期负房价。
独立性
假设每个实例独立于任何其他实例。如果您进行重复测量,例如每位患者进行多次血液检查,则数据点不是独立的。对于依赖数据,您需要特殊的线性回归模型,例如混合效应模型或GEE。如果使用“正常”线性回归模型,则可能会从模型中得出错误的结论。
固定特征
输入特征被视为“固定”。固定意味着它们被视为“给定常量”而不是统计变量。这意味着它们没有测量误差。这是一个相当不切实际的假设。但是,如果没有这种假设,您将需要适应非常复杂的测量误差模型,以解决输入特征的测量误差。通常你不想那样做。
没有多重共线性
您不需要强相关的特征,因为这会影响权重的估计。在两个特征强相关的情况下,估计权重变得有问题,因为特征效果是加性的,并且对于哪个相关特征来归因于效果变得不确定。
4.1.1解释
线性回归模型中权重的解释取决于相应特征的类型。
数字特征:将数字特征增加一个单位会改变估计结果的重量。数字特征的一个例子是房屋的大小。
二进制特征:为每个实例采用两个可能值之一的特征。一个例子是“House with a garden”。其中一个值计为参考类别(在一些编码为0的编程语言中),例如“No garden”。将要素从参考类别更改为其他类别会根据要素的权重更改估计结果。
具有多个类别的分类特征:具有固定数量的可能值的特征。一个例子是“地板类型”的特征,可能的类别是“地毯”,“层压板”和“镶木地板”。处理许多类别的解决方案是单热编码,这意味着每个类别都有自己的二进制列。对于具有L类别的分类特征,您只需要L-1列,因为第L列将具有冗余信息(例如,当列1到L-1对于一个实例都具有值0时,我们知道分类特征此实例采用类别L)。然后,每个类别的解释与二元特征的解释相同。某些语言(如R)允许您以各种方式对分类要素进行编码,如本章后面所述。
截距
β0:截距是“常量特征”的特征权重,对于所有实例始终为1。大多数软件包会自动添加此“1”特征来估计截距。解释是:对于所有数值特征值为零且参考类别的分类特征值的实例,模型预测是截距权重。截距的解释通常是不相关的,因为所有特征值为零的实例通常没有意义。只有当特征标准化(平均值为零,标准差为1)时,解释才有意义。然后,截距反映了所有特征都处于其平均值的实例的预测结果。
通过使用以下文本模板,可以自动解释线性回归模型中的特征。
解释数值特征
特征xk增加一个单位会增加y的预测
所有其他特征值保持固定时的βk单位。
解释分类特征
当将所有其他特征保持固定时,将特征xk从参考类别更改为其他类别会将y的预测增加βk。
解释线性模型的另一个重要衡量指标是R平方测量。 R平方告诉您模型解释了目标结果的总方差有多少。 R平方越高,模型解释数据的效果越好。 计算R平方的公式是:
SSE是错误项的平方和:
SST是数据方差的平方和:
SSE会告诉您在拟合线性模型后剩余多少方差,这是通过预测目标值和实际目标值之间的平方差来衡量的。 SST是目标结果的总方差。 R平方告诉您线性模型可以解释多少方差。 对于模型根本不解释数据的模型,R平方的范围在0之间,对于解释数据中所有方差的模型,R平方的范围为1。
有一个问题,因为R平方随着模型中特征的数量而增加,即使它们根本不包含任何有关目标值的信息。 因此,最好使用调整后的R平方,它考虑了模型中使用的特征数量。 它的计算是:
其中p是特征的数量,n是实例的数量。
解释具有非常低(调整)的R平方的模型没有意义,因为这样的模型基本上不能解释很多方差。 对权重的任何解释都没有意义。
特征重要性
线性回归模型中特征的重要性可以通过其t统计量的绝对值来度量。 t统计量是用其标准误差缩放的估计权重。
让我们来看看这个公式告诉我们的内容:一个特征的重要性随着权重的增加而增加。 这是有道理的。 估计权重的方差越大(=我们对正确值越不确定),该特征就越不重要。 这也是有道理的。
4.1.2示例
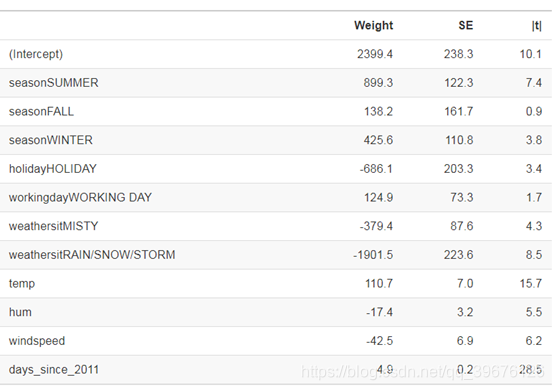
在此示例中,我们使用线性回归模型来预测特定日期租用自行车的数量,给定天气和日历信息。 为了解释,我们检查估计的回归权重。 这些特征包括数字和分类特征。 对于每个特征,该表显示估计的权重,估计的标准误差(SE)和t统计量的绝对值(| t |)。
解释数字特征(温度):当所有其他特征保持固定时,将温度增加1摄氏度会使预测的自行车数量增加110.7。
解释一个分类特征(“weathersit”):与好天气相比,在下雨,下雪或暴风雨时,估计自行车的数量会降低-1901.5 - 再次假设所有其他特征都没有改变。当天气有雾时,预计自行车的数量与好天气相比降低了-379.4,因为所有其他特征保持不变。
所有的解释总是附有“所有其他特征保持不变”的脚注。这是因为线性回归模型的本质。预测目标是加权特征的线性组合。估计的线性方程是特征/目标空间中的超平面(在单个特征的情况下是简单的线)。权重指定超平面在每个方向上的斜率(梯度)。好的一面是,可加性将单个特征效果的解释与所有其他特征隔离开来。这是可能的,因为等式中的所有特征效果(=权重时间特征值)与加号组合。在不好的方面,解释忽略了特征的联合分布。增加一个特征但不改变另一个特征可能导致不切实际或至少不太可能的数据点。例如,增加房间数量可能是不现实的,但不增加房屋的大小。
4.1.6线性模型能否创造良好的解释?
根据构成良好解释的属性来判断,如“人类友好解释”一章所述,线性模型并未创建最佳解释。它们是对比的,但参考实例是一个数据点,其中所有数字特征均为零,并且分类特征位于其参考类别。这通常是一个人为的,毫无意义的实例,不太可能出现在您的数据或现实中。有一个例外:如果所有数字特征均为中心(特征减去特征的平均值)并且所有分类特征都是效果编码,则参考实例是所有特征都采用平均特征值的数据点。这可能也是一个不存在的数据点,但它可能至少更有可能或更有意义。在这种情况下,权重乘以特征值(特征效应)解释了与“平均实例”对比的对预测结果的贡献。良好解释的另一个方面是选择性,可以通过使用较少的特征或通过训练稀疏线性模型在线性模型中实现。但默认情况下,线性模型不会创建选择性解释。线性模型可以创建真实的解释,只要线性方程是特征和结果之间关系的合适模型。线性模型的准确性越低,解释就越不真实。线性使得解释更加通用和简单。我相信,模型的线性特性是人们使用线性模型解释关系的主要因素。