介绍
t-分布邻域嵌入(t-SNE, t-Distributed Stochastic Neighbor Embedding)是一种常用于降维和可视化高维数据的非线性算法。它尤其擅长将高维数据映射到2D或3D空间,以便进行可视化,同时保持数据点之间的相对结构。
t-SNE 是一种基于概率的降维方法,它的目标是保持高维空间中相似数据点的相对距离关系,同时尽可能减少低维空间中相似点的距离差异。
相似度的数学表示
高维空间相似度
t-SNE 通过将每对数据点的相似度表示为条件概率来计算相似度。在高维空间中,对于数据点 x i x_{i} xi和 x j x_{j} xj,我们计算条件概率 p i j p_{ij} pij,表示在给定点 x i x_{i} xi的情况下,点 x j x_{j} xj为其邻居的概率。
这个概率的计算基于高斯分布:
p i j = exp ( − ∥ x i − x j ∥ 2 2 σ i 2 ) ∑ k ≠ i exp ( − ∥ x i − x k ∥ 2 2 σ i 2 ) p_{ij} = \frac{\exp\left(-\frac{\|x_i - x_j\|^2}{2\sigma_i^2}\right)}{\sum_{k \neq i} \exp\left(-\frac{\|x_i - x_k\|^2}{2\sigma_i^2}\right)} pij=∑k=iexp(−2σi2∥xi−xk∥2)exp(−2σi2∥xi−xj∥2)
其中, ∣ ∣ x i − x j ∣ ∣ ||x_{i}-x_{j}|| ∣∣xi−xj∣∣为点 x i x_{i} xi与点 x j x_{j} xj间的距离(默认为欧几里得距离),而 σ \sigma σ是为每个点定义的尺度参数,用来控制高斯分布的宽度。
低维空间相似度
在低维空间中,t-SNE 使用 t-分布(通常是自由度为1的学生t分布,也称为 Cauchy 分布)来度量数据点之间的相似性。t-分布的优势在于,它比高斯分布更有助于将远离的点拉开,使得低维空间中的点更容易分离。
对于低维空间点
y
i
y_{i}
yi和
y
j
y_{j}
yj,其相似度计算为:
q i j = ( 1 + ∥ y i − y j ∥ 2 ) − 1 ∑ k ≠ l ( 1 + ∥ y k − y l ∥ 2 ) − 1 q_{ij} = \frac{\left(1 + \|y_i - y_j\|^2\right)^{-1}}{\sum_{k \neq l} \left(1 + \|y_k - y_l\|^2\right)^{-1}} qij=∑k=l(1+∥yk−yl∥2)−1(1+∥yi−yj∥2)−1
损失函数
t-SNE 的目标是使低维空间中的相似度分布 q i j q_{ij} qij尽可能地接近高维空间中的相似度分布 p i j p_{ij} pij。因此,t-SNE 使用 Kullback-Leibler 散度(KL散度)作为目标函数,来度量这两者之间的差异:
C ( Y ) = ∑ i < j p i j l o g p i j q i j C(Y)=\sum_{i<j}p_{ij}log\frac{p_{ij}}{q_{ij}} C(Y)=∑i<jpijlogqijpij
Barnes-Hut t-SNE优化
Barnes-Hut t-SNE 通过引入 Barnes-Hut 近似 方法来降低计算复杂度,从
O
(
N
2
)
O(N^2)
O(N2)降低到
O
(
N
l
o
g
N
)
O(NlogN)
O(NlogN)。
四叉树(Quadtree)
四叉树是一种递归的空间分区数据结构,主要用于 二维空间(2D)。
基本思想(分治):将一个平面区域反复划分为四个子区域(象限),直到满足某种条件为止(如每个区域内的点数少于某个阈值)。
节点分割:每个节点对应一个矩形区域,子节点表示将该区域划分为的四个子矩形。
应用在 t-SNE 中,低维空间的点对相似度
q
i
j
q_{ij}
qij的计算复杂度为
O
(
N
2
)
O(N^2)
O(N2)。通过四叉树,将远离某点的点簇合并为一个伪点进行计算,从而降低复杂度。
八叉树(Octree)
八叉树是四叉树在 三维空间(3D) 的扩展。过程与四叉树基本一致。
选择 4 和 8 作为分区数量,主要是基于四叉树和八叉树的核心思想:均匀分割空间
FIt-SNE
FIt-SNE 使用 FFT 计算高维数据点之间的引力和斥力,从而替代了 Barnes-Hut t-SNE 的树结构,更加优化了时间复杂度。虽然复杂度仍是
O
(
N
l
o
g
N
)
O(NlogN)
O(NlogN),但在极大的数据集上的效果优于Barnes-Hut t-SNE。
此外,FLt-SNE支持GPU加速。
代码实现
普通的t-SNE:
from sklearn.manifold import TSNE
from sklearn.datasets import make_swiss_roll
import matplotlib.pyplot as plt
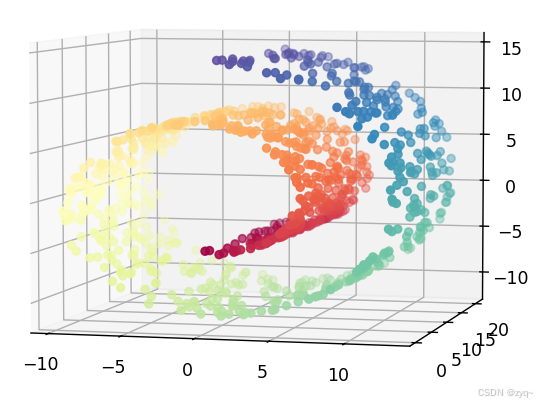
# 生成三维的瑞士卷数据集
X, color = make_swiss_roll(n_samples=1000, noise=0.05)
# 可视化原始高维数据
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=color, cmap=plt.cm.Spectral)
plt.title("Original 3D Swiss Roll")
plt.show()
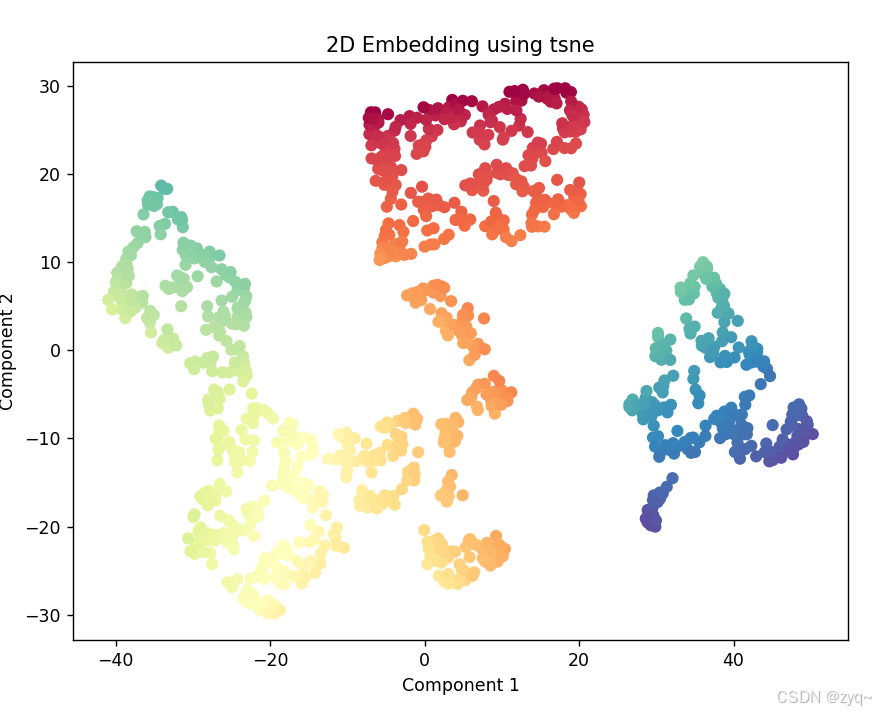
# 创建 t-SNE 对象,设置目标维度为2
tsne = TSNE(n_components=2)
# 降维
X_tsne = tsne.fit_transform(X)
# 可视化降维后的结果
plt.figure(figsize=(8, 6))
plt.scatter(X_tsne[:, 0], X_tsne[:, 1], c=color, cmap=plt.cm.Spectral)
plt.title("2D Embedding using tsne")
plt.xlabel("Component 1")
plt.ylabel("Component 2")
plt.show()
以及使用Barnes-Hut t-SNE需要修改的地方
tsne = TSNE(
n_components=2, # 降维到 2 维
perplexity=30, # 困惑度,控制局部结构
learning_rate=200, # 学习率
n_iter=1000, # 最大迭代次数
method='barnes_hut', # 使用 Barnes-Hut 近似算法
n_jobs=-1, # 并行计算,加速处理
random_state=42 # 固定随机种子,确保结果可复现
)
而Flt-SNE则要用库openTSNE:
from openTSNE import TSNE
from sklearn.datasets import make_swiss_roll
import matplotlib.pyplot as plt
# 生成三维的瑞士卷数据集
X, color = make_swiss_roll(n_samples=1000, noise=0.05)
# 可视化原始高维数据
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=color, cmap=plt.cm.Spectral)
plt.title("Original 3D Swiss Roll")
plt.show()
# 使用 FIt-SNE 进行降维
fit_tsne = TSNE(
n_components=2, # 降维到二维
perplexity=20, # 调整困惑度
learning_rate=200, # 学习率
n_iter=500, # 最大迭代次数
initialization="pca", # 使用 PCA 初始化
random_state=42, # 固定随机种子
# n_jobs=1 # 强制单线程
n_jobs=-1 # 多线程,不知道为什么我多线程跑不出结果,单线程也很慢很慢
)
# 执行降维
X_fit_tsne = fit_tsne.fit(X)
# 可视化降维后的二维结果
plt.figure(figsize=(8, 6))
plt.scatter(X_fit_tsne[:, 0], X_fit_tsne[:, 1], c=color, cmap=plt.cm.Spectral, s=15, edgecolor='k')
plt.title("2D Embedding using FIt-SNE")
plt.xlabel("Component 1")
plt.ylabel("Component 2")
plt.show()