线性回归
1,概述
线性回归(Linear Regression)是机器学习最基本的回归算法之一,通过对自变量和因变量之间的关系进行建模,找出一个拟合最好的线性关系函数。而根据自变量的多少,又可以分为一元回归和多元回归。
2,算法推导
假设银行的贷款额度和借贷人的年龄、薪资水平有关,现在希望根据一组数据,使得我们能够确定出三者之间的线性关系并由此做出合理的借贷额度预测。这里有函数: h θ ( x ) = θ 0 + θ 1 x 1 h_{\theta}(x)=\theta_{0}+\theta_{1} x_{1} hθ(x)=θ0+θ1x1。
其中 θ 0 \theta_{0} θ0为偏置项,也就是我们的常数项。在实际处理时,可以整合进变量所在列向量中,系数为1。
θ 1 \theta_{1} θ1为特征参数, x 1 x_{1} x1为特征值。
进一步的,上式可整合为:
h
θ
(
x
)
=
∑
i
=
0
n
θ
i
x
i
=
θ
T
x
h_{\theta}(x)=\sum_{i=0}^{n} \theta_{i} x_{i}=\theta^{T} x
hθ(x)=i=0∑nθixi=θTx
为了更好的拟合我们模型,对于每组数据我们都希望预测值与真实值之间的误差最小。也就是我们的损失函数为:
J
(
θ
)
=
1
2
m
∑
i
=
1
m
(
y
(
i
)
−
θ
T
x
(
i
)
)
2
J(\theta)=\frac{1}{2m} \sum_{i=1}^{m}\left(y^{(i)}-\theta^{T} x^{(i)}\right)^{2}
J(θ)=2m1i=1∑m(y(i)−θTx(i))2
这里使用平方误差作为度量依据,也就是预测值和真实值之间残差的平方和。(也就是最小二乘法)
为了便于后续的分析,我们又加上了一个 1 2 \frac{1}{2} 21 的系数。
此时,问题就转换为求解使得 J ( θ ) J(\theta) J(θ) 最小时的 θ \theta θ 值。
方法一:正规方程法
将上述(2)式转换为矩阵形式:
J
(
θ
)
=
1
2
(
X
θ
−
y
)
T
(
X
θ
−
y
)
J(\theta)=\frac{1}{2}(X \theta-y)^{T}(X \theta-y)
J(θ)=21(Xθ−y)T(Xθ−y)
一个数的平方可以写为其矩阵和转置矩阵相乘的形式。
上式中** X θ − y X \theta-y Xθ−y**为一个 n 行 1 列矩阵,x 为 m 行 n 列矩阵。
对
θ
\theta
θ 求偏导:
∇
θ
J
(
θ
)
=
∇
θ
(
1
2
(
X
θ
−
y
)
T
(
X
θ
−
y
)
)
=
∇
θ
(
1
2
(
θ
T
X
T
X
θ
−
θ
T
X
T
y
−
y
T
X
θ
+
y
T
y
)
)
=
1
2
(
2
X
T
X
θ
−
2
X
T
y
)
=
X
T
X
θ
−
X
T
y
\begin{array}{l} \nabla_{\theta} J(\theta)=\nabla_{\theta}\left(\frac{1}{2}(X \theta-y)^{T}(X \theta-y)\right) &\\ =\nabla_{\theta}\left(\frac{1}{2}\left(\theta^{T} X^{T} X \theta-\theta^{T} X^{T} y-y^{T} X \theta+y^{T} y\right)\right) \\ =\frac{1}{2}\left(2 X^{T} X \theta-2X^{T} y\right) \\=X^{T} X \theta-X^{T} y \end{array}
∇θJ(θ)=∇θ(21(Xθ−y)T(Xθ−y))=∇θ(21(θTXTXθ−θTXTy−yTXθ+yTy))=21(2XTXθ−2XTy)=XTXθ−XTy
偏导置为 0:
θ
=
(
X
T
X
)
−
1
X
T
y
\theta=\left(X^{T} X\right)^{-1} X^{T} y
θ=(XTX)−1XTy
式(5)即为最终求解式。但前提是
X
T
X
X^{T} X
XTX可逆。当样本数少于特征数时(m<n)即不满足条件。
方法二:梯度下降法
梯度:多元函数对参数求偏导,将每个参数的偏导数组成一个向量,则该向量即为梯度。
其几何意义就是函数值增加最快的方向。
由上述分析,为找到损失函数的最小值,我们应该按照梯度的相反方向寻找目标值。即梯度下降的方式寻找损失函数最小值。
此时损失函数的梯度为:
∂
J
(
θ
)
∂
θ
j
\frac{\partial J(\theta)}{\partial \theta_{j}}
∂θj∂J(θ),另外设置步长 α 控制下降的幅度,α 也叫学习率。不断的进行梯度下降,直到梯度达到我们设定的阀值,即停止算法。模型参数更新公式如下:
θ
j
:
=
θ
j
−
α
∂
J
(
θ
)
∂
θ
j
\theta_{j} := \theta_{j} -α\frac{\partial J(\theta)}{\partial \theta_{j}}
θj:=θj−α∂θj∂J(θ)
由此,对于损失函数:
J
(
θ
)
=
1
2
m
∑
i
=
1
m
(
y
i
−
h
o
(
x
i
)
)
2
J(\theta)=\frac{1}{2 m} \sum_{i=1}^{m}\left(y^{i}-h_{o}\left(x^{i}\right)\right)^{2}
J(θ)=2m1i=1∑m(yi−ho(xi))2有:
∂
J
(
θ
)
∂
θ
j
=
−
1
m
∑
i
=
1
m
(
y
i
−
h
θ
(
x
i
)
)
x
j
i
\frac{\partial J(\theta)}{\partial \theta_{j}}=-\frac{1}{m} \sum_{i=1}^{m}\left(y^{i}-h_{\theta}\left(x^{i}\right)\right) x_{j}^{i} \quad
∂θj∂J(θ)=−m1i=1∑m(yi−hθ(xi))xji
整理得:
θ
j
:
=
θ
j
−
α
m
∑
i
=
1
m
(
h
θ
(
x
i
)
−
(
y
i
)
)
x
j
\theta_{j}:=\theta_{j}-\frac{α}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{i}\right)-(y^{i}\right)) x_{j}
θj:=θj−mαi=1∑m(hθ(xi)−(yi))xj
进一步的,我们的问题就转换成了,利用 8 式,不断更新模型参数 θ,直到模型收敛或梯度达到阈值。
线性回归的优化:步长优化,模型初始值优化,数据归一化处理。
梯度下降法分类:批量梯度下降,随机梯度下降,小批量梯度下降。
-
批量梯度下降法(Batch Gradient Descent,BGD),选取全部样本做梯度下降
-
随机梯度下降法(Stochastic Gradient Descent,SGD),随机选取一个样本做梯度下降(重复多次)
-
小批量梯度下降法(Mini-batch Gradient Descent,MBGD),随机选取部分样本做梯度下降
3,手写线性回归
按照上面的整理的思路,我们自己手动实现一个线性回归:
import numpy as np
# 可以看到我们按照如y=10x+b的形式设置实验变量
train_x = np.array([0.1, 0.2, 0.6, 1.2, 1.4])
train_y = np.array([1, 2.4, 5.5, 11.2, 15.6])
times = 3000 # 迭代次数
lrate = 0.01 # 学习率,即步长,不能太大
w0, w1 = [1], [1] # 初始化模型参数
losses = [] # 保存每次迭代过程中的损失
epoches = [] # 保存每次迭代过程的索引
for i in range(1, times+1):
epoches.append(i)
loss = ((w0[-1] + w1[-1] * train_x - train_y)
** 2).sum() / 2 # 对应公式(2),m=2;脚标-1表示每次都使用最新的参数
losses.append(loss)
# 每200次做打印
if i % 200 == 0:
print('{:4}> w0={:.6f},w1={:.6f},loss={:.6f}'.format(
epoches[-1], w0[-1], w1[-1], losses[-1]))
# 每次梯度下降过程,需要求出w0和w1的修正值,求修正值需要推导loss函数在w0及w1方向的偏导数
d0 = (w0[-1] + w1[-1] * train_x - train_y).sum() # 更新w0
d1 = ((w0[-1] + w1[-1] * train_x - train_y) * train_x).sum() # 更新w1
# w0和w1的值根据步长做梯度下降不断修正(BGD)
w0.append(w0[-1] - lrate * d0)
w1.append(w1[-1] - lrate * d1)
print(w0[-1], w1[-1]) # 打印最终的模型参数
200> w0=0.774735,w1=9.319904,loss=2.521114
400> w0=0.013325,w1=10.221678,loss=1.665090
600> w0=-0.123439,w1=10.383654,loss=1.637472
800> w0=-0.148004,w1=10.412748,loss=1.636581
1000> w0=-0.152416,w1=10.417973,loss=1.636552
1200> w0=-0.153209,w1=10.418912,loss=1.636552
1400> w0=-0.153351,w1=10.419081,loss=1.636551
1600> w0=-0.153377,w1=10.419111,loss=1.636551
1800> w0=-0.153381,w1=10.419116,loss=1.636551
2000> w0=-0.153382,w1=10.419117,loss=1.636551
2200> w0=-0.153382,w1=10.419118,loss=1.636551
2400> w0=-0.153382,w1=10.419118,loss=1.636551
2600> w0=-0.153382,w1=10.419118,loss=1.636551
2800> w0=-0.153382,w1=10.419118,loss=1.636551
3000> w0=-0.153382,w1=10.419118,loss=1.636551
-0.15338235290769545 10.41911764701917
4,Sklearn 实例讲解
我们利用Sklearn库中提供的模型进行上述实验:
模型的周期(也可以说是机器学习的生命周期):
- 数据收集
- 数据处理
- 模型训练
- 模型预测
- 模型评估
- 模型展示
- 模型存储
import numpy as np
import sklearn.linear_model as lm
import matplotlib.pyplot as mp
import sklearn.metrics as sm
import pickle
# 1,加载数据源
x, y = np.loadtxt('python/ml/sklearn_lin.txt', delimiter=',', unpack=True)
# print(x) # 返回的是x,y两列,一维数组类型
# 2,做数据处理
# 将输入改变为矩阵sparse matrix
x = x.reshape(-1, 1) # -1代表最大行数,变成n行1列
# print(x)
# 3,模型训练
model = lm.LinearRegression()
model.fit(x, y)
# 4,模型预测
pred_y = model.predict(x)
print(y)
print(pred_y)
# 5,模型评估
print('平均绝对值误差:', sm.mean_absolute_error(y, pred_y))
print('平均平方误差:', sm.mean_squared_error(y, pred_y))
print('中位绝对值误差:', sm.median_absolute_error(y, pred_y))
print('R2得分:', sm.r2_score(y, pred_y)) # (0,1]区间的分值。分数越高,误差越小
# 6,模型展示
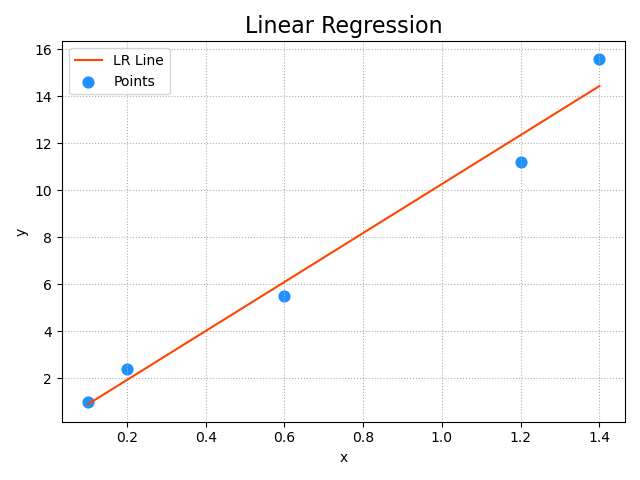
mp.figure("Linear Regression", facecolor='lightgray')
mp.title('Linear Regression', fontsize=16)
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
mp.xlabel('x')
mp.ylabel('y')
mp.scatter(x, y, s=60, marker='o', c='dodgerblue', label='Points')
mp.plot(x, pred_y, c='orangered', label='LR Line')
mp.tight_layout()
mp.legend()
mp.show()
# 7,模型持久化存储
with open('python/ml/sklearn_lin_model.pkl', 'wb') as f:
pickle.dump(model, f)
print('Model dump success!')
'''
# 8,从文件中加载模型
with open('python/ml/sklearn_lin_model.pkl', 'rb') as f:
model = pickle.load(f)
'''
5,实战
使用sklearn中的数据集,及线性回归模型,预测波士顿房价。
数据集共有506条数据和13个特征值.以下是数据集参数:
data:表示特征值;
target:目标,即标签;
feature_names:各个特征的名称;
DESCR:特征描述;
filename:数据集名称及数据集的当前路径.
特征值描述如下:

使用jupyter notebook逐步将代码加载到内存,并测试功能。
In [1]:
#使用sklearn中自带数据集波士顿放假预测
from sklearn. datasets import 1oad_ boston
#返回一个字典型的数据集
boston = load_ boston()
boston. keys ()
0ut[1]: dict_ keys([' data',’target’ ,’feature_ _names' ,DESCR' ,’filename’ ])
In [2]:
boston.filename
0ut[2]:’ c:\\program files\\lib\\site-packages\\sklearn\\datasets\\data\\boston_ house_ prices. csv'
In [3]: boston. data. shape
0ut[3]: (506, 13)
In [4]:
#利用pandas处理数据集
import pandas as pd
bos = pd.DataFrame(boston.data)
#为数据加上对应的描述
bos.columns = boston.feature_names
#sklearn中数据集默认标签和特征值是分开的,这里增加一列
bos['PRICE'] = boston.target
#默认加载前5个
bos.head()
加载情况:
In [5]:
#将数据集划分为测试和训练数据集,特征值用X,标签用y
X = boston.data
y = boston.target
#train_test_split函数,随机种子保证分割时不随机,size为训练集和测试机占比
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(boston.data,boston.target,test_size=0.3,random_state=0)
#回归模型
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(X_train,y_train) #训练模型
y_pred = lr.predict(X_test) #预测模型
print(y_pred)
0ut[5]:
[24.936 23.752 29.326 11.975 21.373 19.191 20.572 21.212 19.046 20.355
5.441 16.937 17.155 5.393 40.203 32.313 22.462 36.501 31.037 23.171
24.748 24.499 20.66 30.455 22.325 10.189 17.443 18.261 35.633 20.82
18.272 17.72 19.338 23.623 28.978 19.45 11.132 24.818 18.053 15.597
26.21 20.811 22.173 15.484 22.623 24.886 19.748 23.047 9.846 24.364
21.478 17.621 24.392 29.951 13.572 21.536 20.533 15.034 14.323 22.119
17.073 21.541 32.968 31.372 17.786 32.751 18.748 19.214 19.42 23.081
22.877 24.064 30.528 28.715 25.908 5.176 36.871 23.77 27.261 19.258
28.419 19.301 18.949 38.002 39.441 23.723 24.837 16.52 25.997 16.74
15.487 13.528 24.129 30.769 22.187 19.885 0.423 24.868 16.057 17.425
25.498 22.352 32.666 22.044 27.298 23.203 6.862 14.869 22.318 29.181
33.226 13.244 19.672 20.75 12.023 23.501 5.557 19.876 9.271 44.818
30.56 12.444 17.332 21.483 23.527 20.499 35.092 13.226 20.703 35.356
19.451 13.816 14.157 23.037 15.075 30.966 25.232 15.438 24.064 9.931
15.016 21.061 32.871 27.809 25.913 15.279 30.975 27.811 14.507 7.574
28.335 25.043]
in[6]:
import numpy as np
np.set_printoptions(precision=3,suppress=True)#第三行数据取消科学技术法
print("w0={0:.3f}".format(lr.intercept_))#获得模型的截距
print("W={}".format(lr.coef_))#每个特征的权重
out[6]:
w0=37.937
W=[ -0.121 0.044 0.011 2.511 -16.231 3.859 -0.01 -1.5 0.242
-0.011 -1.018 0.007 -0.487]
数据可视化处理:
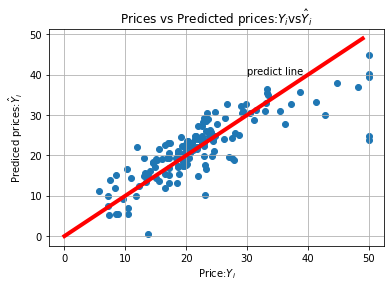
in[7]:import matplotlib.pyplot as pltplt.scatter(y_test,y_pred)plt.xlabel("Price:$Y_i$")plt.ylabel("Prediced prices:$\hat{Y}_i$")#设置坐标轴plt.title("Prices vs Predicted prices:$Y_i$vs$\hat{Y}_i$")plt.grid()x = np.arange(0,50)y = xplt.plot(x,y,color='red',lw=4)plt.text(30,40,'predict line')plt.savefig("prices.eps")
in[8]:#对预测结果进行评估from sklearn import metricsmse = metrics.mean_squared_error(y_test,y_pred)print("mse:",mse)out[8]:mse: 27.195965766883152
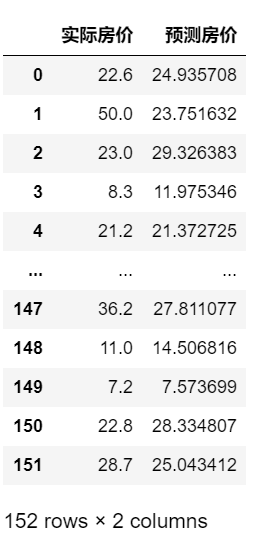
in[9]:#输出对比数据df = pd.DataFrame({'实际房价':y_test,'预测房价':y_pred})df
输出比对效果如下:
参考链接