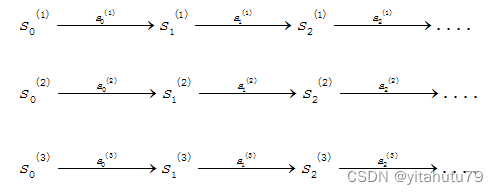马尔可夫决策过程
本文介绍了马尔可夫决策过程,首先给出了马尔可夫决策过程的定义形式,其核心是在时序上的各种状态下如何选择最优决策得到最大回报的决策序列,通过贝尔曼方程得到累积回报函数;然后介绍两种基本的求解最优决策的方法,值迭代和策略迭代,同时分析了两种方法的适用场景;最后回过头来介绍了马尔科夫决策过程中的参数估计问题:求解-即在该状态下采取该决策到底下一状态的概率。
一、马尔科夫决策过程:
机器学习算法(有监督,无监督,弱监督)中,马尔科夫决策过程是弱监督中的一类叫增强学习。增加学习与传统的有监督和无监督不同的地方是,这些方法都是一次性决定最终结果的,而无法刻画一个决策过程,无法直接定义每一次决策的优劣,也就是说每一次的决策信息都是弱信息,所以某种程度上讲,强化学习也属于弱监督学习。从模型角度来看,也属于马尔科夫模型,其与隐马尔科夫模型有非常强的可比性。
下面是一个常用的马尔科夫模型的划分关系
不考虑动作考虑动作状态完全可见马尔科夫链(MC)马尔科夫决策过程(MDP)状态不完全可见隐马尔科夫模型(HMM)不完全可观察马尔科夫决策过程(POMDP)
马尔科夫决策过程
马尔科夫决策过程由五元组组成
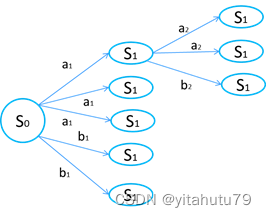
有了上面的定义之后,一个完整的马尔科夫决策过程状态转移图如下:
也就是说最优决策下对应的累积回报一定不小于一般的决策下的累积回报。
值得注意是,最优决策是出于全局考虑的,是从所有状态下出发到得到的累积回报的加和最大,这就意味着决策函数不保证其中每一个状态出发根据决策函数得到的累积回报都是最大的。
最优决策
也许上面的目标函数还不清晰,如何求解最有决策,如何最大化累积回报
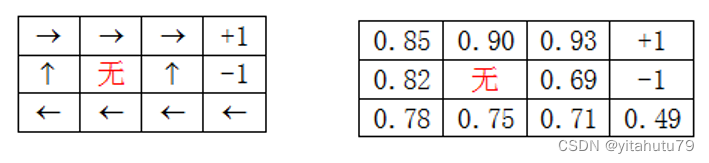
下面结合例子来介绍如何求解上面的目标函数。且说明累积回报函数本身就是一个过程的累积回报,回报函数[公式]才是每一步的回报。
下面再来看求解上述最优问题,其中 就是以s为初始状态沿着决策函数走到结束状态的累积回报。
值迭代
内循环迭代的的处理方法有两种:
同步迭代:即在一次循环过程中,累积回报不更新,而是计算完所有的累积回报之后,再统一更新。
异步迭代,即在一次循环过程中,每计算完一个初始状态下累积回报就立即更新,不需要等到所有的累积回报都计算出来之后再更新。
策略迭代
值迭代是使累积回报值最优为目标进行迭代,而策略迭代是借助累积回报最优即策略最优的等价性,进行策略迭代。
同样,收敛性也是值得探讨的,这里简单的思考一下,由于奖励状态和惩罚状态的分布,以及累积回报唯一确定决策函数,那么未达到最优决策,必然累积回报和决策函数处于不稳定的状态,而只有当到达最优决策时,才有:
所以该过程就是在a步由决策函数确定累积回报,然后最大化累积回报来更新决策,如此反复,则有最优决策。值迭代和策略迭代比较:可以看出策略迭代涉及从决策函数到累积回报的解线性方程组的步骤,值迭代则是反复的,所以策略迭代更适合处理少量状态的情况,一般10000以内还是可以接受的。
MDP中的参数估计
回过头来再来看前面的马尔科夫决策过程的定义是一个五元组,一般情况下,五元组应该是我们更加特定的问题建立马尔科夫决策模型时该确定的,并在此基础上来求解最优决策。所以在求解最优决策之前,我们还需更加实际问题建立马尔科夫模型,建模过程就是确定五元组的过程,其中我们仅考虑状态转移概率,那么也就是一个参数估计过程。(其他参数一般都好确定,或设定)。
假设,在时间过程中,我们有下面的状态转移路径:
整个流程就是在策略迭代的基础上,同时进行了参数估计。
二、代码实战:
A、马尔可夫决策过程值迭代
/***
马尔科夫决策过程值迭代,关键在于第一次迭代要例外,
因为目标状态是一个终止状态,放到迭代循环里面会出现
临近的状态回报函数无限的,发散。
迭代过程采用的是异步迭代,即每一次内层循环找到更优的
回报就立即更新最大回报,以便与之相邻的状态能立即更新到最优
*/
/****
值迭代
同步更新
12*12*7
*/
while(!flag)
{
flag=1;
for(i=0; i<size; i++)
{
if(action[i]>0||action[i]==0)
maxreward[i]=reward[i]+maxreward[action[i]];
else
maxreward[i]=reward[i];
}//放到这意味着同步更新,count=1008是12*12的7倍,即扫了7遍
for(i=0; i<size; i++)//对每一个状态求最大的V(s)
{
for(j=0; j<size; j++)//策略迭代的话这里其实可以换做扫一遍策略集,这也就是和值迭代不同的地方
{
//cout<<"i="<<i<<" "<<maxreward[i]<<" "<<endl;
if(matrix[i][j]==1&&maxreward[j]>maxreward[i]-reward[i]+0.0001)//更新累积回报
{
action[i]=j;
//if(action[i]>0||action[i]==0)
//maxreward[i]=reward[i]+maxreward[action[i]];//放到这是异步更新,
//else
// maxreward[i]=reward[i];
flag=0;//当累积回报不再更新,即不进入该if,那么就结束迭代
}
count++;
}
}
}
B、马尔可夫决策过程策略迭代
while(!flag)
{
flag=1;
for(i=0; i<size; i++)//对每一个状态求最大的V(s)
{
for(j=0; j<ACTION; j++)//策略迭代的话这里其实可以换做扫一遍策略集,这也就是和值迭代不同的地方
{
//cout<<"i="<<i<<" "<<maxreward[i]<<" "<<endl;
if(matrix[i][ac[j]+i]==1&&maxreward[ac[j]+i]>maxreward[i]-reward[i]+0.0001)
{
action[i]=j;
//if(reward[i]!=1&&reward[i]!=-1)
maxreward[i]=reward[i]+maxreward[ac[j]+i];
//else
// maxreward[i]=reward[i];
flag=0;
}
count++;
}
}
}
C、马尔可夫决策过程动态规划版
/**
4 非递归动态规划
从最终状态出发,采用广度遍历不断的更新其上一状态的累积回报
*/
/*
while(q!=NULL)//这里图的广度遍历没有用到队列,但也用到了队列的思想
//对于当前步能到达的节点用链表连接起来,然后逐渐进行下一步的能到达的节点进行入链(入队列),同样是一种先进先出思想
{
for(i=0; i<size; i++) //由于不是策略迭代,只能遍历所有的状态,找出能到的,且更优的
{
if(matrix[i][q->data]==1&&maxreward[i]<0)//double类型比较大小的偏差,加上一个小数作为精度
{
maxreward[i]=reward[i]+maxreward[q->data];
p=(subset *)malloc(sizeof(subset)*1);
p->data=i;
p->next=NULL;
q=maxsubset;
while((q->next)!=NULL)
q=q->next;
q->next=p;
}
count++;
}
maxsubset->next=maxsubset->next->next;//删除当前节点,即当前步下能到达的节点都已经走完了,可出队列了
q=maxsubset->next;//
}
![[公式]](/image/aHR0cHM6Ly9pLWJsb2cuY3NkbmltZy5jbi9ibG9nX21pZ3JhdGUvOWFjMjFjM2I1NDMyOTE0MTE1NTQ4NWMzYjdlNTZiMGIucG5n)






![[公式]](/image/aHR0cHM6Ly9pLWJsb2cuY3NkbmltZy5jbi9ibG9nX21pZ3JhdGUvOWIwMTA1NTViZjk4YzQ4YmU2NTY5YjMyY2U2MTlmNmIucG5n)