机器学习中总是会碰见调参这种枯燥无味且消耗时间的事情,所幸,有很多可以帮助你自动调参的库以及相应的方法,在这里统一总结一下吧。
一、随机森林超参数优化- RandomSearch和GridSearch
(1)RandomSearch
原理:
超参数优化也就是常说的调参,python-sklearn里常用的有GridSearchCV和RandomizedSearchCV可以用。其中GridSearchCV的原理很简明,就是程序去挨个尝试每一组超参数,然后选取最好的那一组。可以想象,这个是比较费时间的,面临着维度灾难。因此James Bergstra和Yoshua Bengio在2012年提出了超参数优化的RandomSearch方法。
RandomizedSearchCV是在论文的基础上加入了cross-validation
RandomSearchCV是如何"随机搜索"的:
考察其源代码,其搜索策略如下:
(a)对于搜索范围是distribution的超参数,根据给定的distribution随机采样;
(b)对于搜索范围是lit的超参数,在给定的list中等概率采样;
(c)对a、b两步中得到的n_iter组采样结果,进行遍历。
(补充)如果给定的搜索范围均为list,则不放回抽样n_iter次。
更详细的可以参考sklearn-RandomizedSearchCV的ParameterSampler类的代码。
为什么RandomSearchCV会有效?
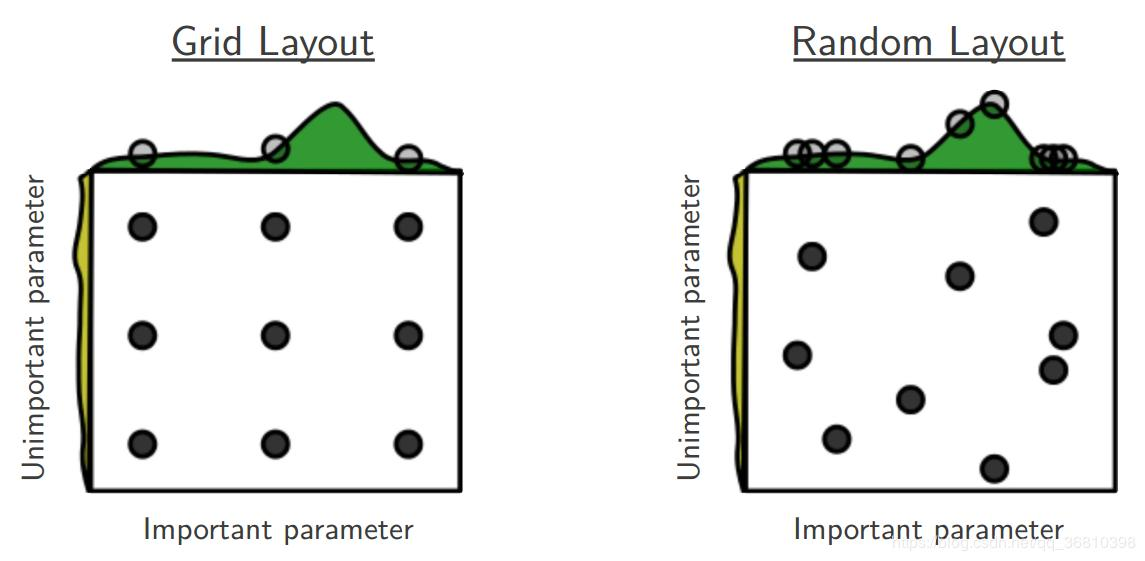
(a)目标函数为 f(x,y)=g(x)+h(y),其中绿色为g(x),黄色为h(y),目的是求f的最大值。
(b)其中由于g(x)数值上要明显大于h(y),因此有f(x,y)=g(x)+h(y)≈g(x),也就是说在整体求解f(x,y)最大值的过程中,g(x)的影响明显大于h(y)。
(c)两个图都进行9次实验(搜索),可以看到左图实际探索了各三个点(在横轴和纵轴上的投影均为3个),而右图探索了9个不同的点(横轴纵轴均是,不过实际上横轴影响更大)。
(d)右图更可能找到目标函数的最大值。
因此引入随机因素在某些情况下可以提高寻优效率。
下面是具体代码
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import RandomizedSearchCV
import numpy as np
from pprint import pprint
from sklearn.datasets import load_iris
if __name__=='__main__':
# Number of trees in random forest
n_estimators = [int(x) for x in np.linspace(start = 200, stop = 2000, num = 10)]
# Number of features to consider at every split
max_features = ['auto', 'sqrt']
# Maximum number of levels in tree
max_depth = [int(x) for x in np.linspace(10, 110, num = 11)]
max_depth.append(None)
# Minimum number of samples required to split a node
min_samples_split = [2, 5, 10]
# Minimum number of samples required at each leaf node
min_samples_leaf = [1, 2, 4]
# Method of selecting samples for training each tree
bootstrap = [True, False]
# Create the random grid
random_grid = {'n_estimators': n_estimators,
'max_features': max_features,
'max_depth': max_depth,
'min_samples_split': min_samples_split,
'min_samples_leaf': min_samples_leaf,
'bootstrap': bootstrap}
pprint(random_grid)
#导入数据
data=load_iris()
# 使用随机网格搜索最佳超参数
# 首先创建要调优的基本模型
rf = RandomForestRegressor()
# 随机搜索参数,使用3倍交叉验证
# 采用100种不同的组合进行搜索,并使用所有可用的核心
rf_random = RandomizedSearchCV(estimator = rf, param_distributions = random_grid, n_iter = 100, cv = 3, verbose=2, random_state=42, n_jobs = -1)
# Fit模型
rf_random.fit(data.data, data.target)
print(rf_random.best_params_)(2)GridSearch网格搜索
#下面是网格搜索:
from sklearn.model_selection import GridSearchCV
data = load_iris()
# Create the parameter grid based on the results of random search
param_grid = {
'bootstrap': [True, False],
'max_depth': [int(x) for x in np.linspace(10, 110, num = 11)],
'max_features': ['auto', 'sqrt'],
'min_samples_leaf': [1, 2, 4],
'min_samples_split': [2, 5, 10],
'n_estimators': [int(x) for x in np.linspace(start = 200, stop = 2000, num = 10)]
}
# Create a based model
rf = RandomForestRegressor()
# Instantiate the grid search model
grid_search = GridSearchCV(estimator=rf, param_grid=param_grid, cv=3, n_jobs=-1, verbose=2)
grid_search.fit(data.data, data.target)
pprint(grid_search.best_params_)
best_grid = grid_search.best_estimator_
grid_accuracy = evaluate(best_grid, data.data, data.target)
pprint(best_grid)
pprint(grid_accuracy)二、 Hyperopt自动化超参数调优- 贝叶斯优化
网格搜索和随机搜索则对ml模型超参数的优化能取得不错的效果,但是需要大量运行时间去评估搜索空间中并不太可能找到最优点的区域。因此越来越多的的超参数调优过程都是通过自动化的方法完成的,它们旨在使用带有策略的启发式搜索(informed search)在更短的时间内找到最优超参数。
贝叶斯优化是一种基于模型的用于寻找函数最小值的方法。近段时间以来,贝叶斯优化开始被用于机器学习超参数调优,结果表明,该方法在测试集上的表现更加优异,并且需要的迭代次数小于随机搜索。
Python 环境下有一些贝叶斯优化程序库,它们目标函数的代理算法有所区别。本部分主要介绍「Hyperopt」库,它使用树形 Parzen 评估器(TPE,https://papers.nips.cc/paper/4443-algorithms-for-hyper-parameter-optimization.pdf)作为搜索算法,其他的 Python 库还包含「Spearmint」(高斯过程代理)和「SMAC」(随即森林回归)。
贝叶斯优化问题有四个组成部分:
1)目标函数:我们想要最小化的对象,这里指带超参数的机器学习模型的验证误差
2)域空间:待搜索的超参数值
3)优化算法:构造代理模型和选择接下来要评估的超参数值的方法
4)结果的历史数据:存储下来的目标函数评估结果,包含超参数和验证损失
通过以上四个步骤,我们可以对任意实值函数进行优化(找到最小值)。
详解:
1)目标函数
模型训练目的是最小化目标函数,所以输出为需要最小化的实值——交叉验证损失。Hyperopt 将目标函数作为黑盒处理,因为这个库只关心输入和输出是什么。为了找到使损失最小的输入值。
cross_val_score
对衡量的estimator,它默认返回的是一个array,包含K folder情况下的各次的评分,一般采用mean()。 需要确定这个estimator默认的 scoring 是什么,它的值是越大越匹配还是越小越匹配。如果自己指定了scoring,一定要确定这个scoring值的意义,切记切记! 而如果用户不指定,一般对于Classification类的estimator,使用accuracy,它是越大越好,那么,hyperopt里面的loss的值就应该是对这个值取负数,因为hyperopt通过loss最小取找最佳匹配。 可以把feature的normalize或者scale作为一个choice,然后看看是否更合适。如果更合适,best里面就会显示 normalize 为1。
from sklearn.datasets import load_iris
from sklearn import datasets
from sklearn.preprocessing import normalize, scale
from hyperopt import fmin, tpe, hp, STATUS_OK, Trials
iris = load_iris()
X = iris.data
y = iris.target
def hyperopt_train_test(params):
X_ = X[:]
# 因为下面的两个参数都不属于KNeighborsClassifier支持的参数,故使用后直接删除
if 'normalize' in params:
if params['normalize'] == 1:
X_ = normalize(X_)
del params['normalize']
if 'scale' in params:
if params['scale'] == 1:
X_ = scale(X_)
del params['scale']
clf = KNeighborsClassifier(**params)
return cross_val_score(clf, X_, y).mean()
space4knn = {
'n_neighbors': hp.choice('n_neighbors', range(1,50)),
'scale': hp.choice('scale', [0, 1]), # 必须是choice,不要用quniform
'normalize': hp.choice('normalize', [0, 1])
}
def f(params):
acc = hyperopt_train_test(params)
return {'loss': -acc, 'status': STATUS_OK} #注意这里的负号
trials = Trials()
best = fmin(f, space4knn, algo=tpe.suggest, max_evals=100, trials=trials)
print best例二,也是取负
def objective(trial):
C=trial.suggest_loguniform('C', 10e-10, 10)
model=LogisticRegression(C=C, class_weight='balanced',max_iter=10000, solver='lbfgs', n_jobs=-1)
score=-cross_val_score(model, Xtrain, Ytrain, cv=kf, scoring='roc_auc').mean()
return score实际GBM完整的目标函数
import lightgbm as lgb
from hyperopt import STATUS_OK
N_FOLDS = 10
# Create the dataset
train_set = lgb.Dataset(train_features, train_labels)
def objective(params, n_folds = N_FOLDS):
"""Objective function for Gradient Boosting Machine Hyperparameter Tuning"""
# Perform n_fold cross validation with hyperparameters
# Use early stopping and evalute based on ROC AUC
cv_results = lgb.cv(params, train_set, nfold = n_folds, num_boost_round = 10000, early_stopping_rounds = 100, metrics = 'auc', seed = 50)
#此部分为核心代码,
# Extract the best score
best_score = max(cv_results['auc-mean'])
# Loss must be minimized
loss = 1 - best_score
# Dictionary with information for evaluation
return {'loss': loss, 'params': params, 'status': STATUS_OK}2)域空间
贝叶斯优化中,域空间对每个超参数来说是一个概率分布而不是离散的值。因为很难确定不同数据集之间的最佳模型设定区间,此处主要采用贝叶斯算法进行推理。
此外,模型中有些参数是不需要调优的。以GBM为例,除了n_estimator之外,还有10个左右的参数需要调整。因此我们采用不同的分布来定义每个参数的域空间
from hyperopt import hp
# Define the search space
space = {
'class_weight': hp.choice('class_weight', [None, 'balanced']),
'boosting_type': hp.choice('boosting_type',
[{'boosting_type': 'gbdt',
'subsample': hp.uniform('gdbt_subsample', 0.5, 1)},
{'boosting_type': 'dart',
'subsample': hp.uniform('dart_subsample', 0.5, 1)},
{'boosting_type': 'goss'}]),
'num_leaves': hp.quniform('num_leaves', 30, 150, 1),
'learning_rate': hp.loguniform('learning_rate', np.log(0.01), np.log(0.2)),
'subsample_for_bin': hp.quniform('subsample_for_bin', 20000, 300000, 20000),
'min_child_samples': hp.quniform('min_child_samples', 20, 500, 5),
'reg_alpha': hp.uniform('reg_alpha', 0.0, 1.0),
'reg_lambda': hp.uniform('reg_lambda', 0.0, 1.0),
'colsample_bytree': hp.uniform('colsample_by_tree', 0.6, 1.0)
}不同分布名称含义:
choice:类别变量
quniform:离散均匀分布(在整数空间上均匀分布)
uniform:连续均匀分布(在浮点数空间上均匀分布)
loguniform:连续对数均匀分布(在浮点数空间中的对数尺度上均匀分布)
- hp.pchoice(label,p_options)以一定的概率返回一个p_options的一个选项。这个选项使得函数在搜索过程中对每个选项的可能性不均匀。
- hp.uniform(label,low,high)参数在low和high之间均匀分布。
- hp.quniform(label,low,high,q),参数的取值round(uniform(low,high)/q)*q,适用于那些离散的取值。
- hp.loguniform(label,low,high) 返回根据 exp(uniform(low,high)) 绘制的值,以便返回值的对数是均匀分布的。
优化时,该变量被限制在[exp(low),exp(high)]区间内。 - hp.randint(label,upper) 返回一个在[0,upper)前闭后开的区间内的随机整数。
- hp.normal(label, mu, sigma) where mu and sigma are the mean and standard deviation σ , respectively. 正态分布,返回值范围没法限制。
- hp.qnormal(label, mu, sigma, q)
- hp.lognormal(label, mu, sigma)
- hp.qlognormal(label, mu, sigma, q)
定义与空间后,可以选择一个样本来查看典型样本形式
# Sample from the full space
example = sample(space)
# Dictionary get method with default
subsample = example['boosting_type'].get('subsample', 1.0)
# Assign top-level keys
example['boosting_type'] = example['boosting_type']['boosting_type']
example['subsample'] = subsample
example3)搜索算法
algo指定搜索算法,目前支持以下算法:
①随机搜索(hyperopt.rand.suggest)
②模拟退火(hyperopt.anneal.suggest)
③TPE算法(hyperopt.tpe.suggest,算法全称为Tree-structured Parzen Estimator Approach)
尽管从概念上来说,这是贝叶斯优化最难的一部分,但在 Hyperopt 中创建优化算法只需一行代码。使用树形 Parzen 评估器(Tree Parzen Estimation,以下简称 TPE)的代码如下:
from hyperopt import tpe
# Algorithm
tpe_algorithm = tpe.suggest4)结果历史数据
想知道背后的发展进程,可以使用「Trials」对象,它将存储基本的训练信息,还可以使用目标函数返回的字典(包含损失「loss」和参数「params」)
from hyperopt import Trials
# Trials object to track progress
bayes_trials = Trials()Trials只是用来记录每次eval的时候,具体使用了什么参数以及相关的返回值。这时候,fn的返回值变为dict,除了loss,还有一个status。Trials对象将数据存储为一个BSON对象,可以利用MongoDB做分布式运算。
from hyperopt import fmin, tpe, hp, STATUS_OK, Trials
fspace = {
'x': hp.uniform('x', -5, 5)
}
def f(params):
x = params['x']
val = x**2
return {'loss': val, 'status': STATUS_OK}
trials = Trials()
best = fmin(fn=f, space=fspace, algo=tpe.suggest, max_evals=50, trials=trials)
print('best:', best)
print('trials:')
for trial in trials.trials[:2]:
print(trial)对于STATUS_OK的返回,会统计它的loss值,而对于STATUS_FAIL的返回,则会忽略。
可以通过这里面的值,把一些变量与loss的点绘图,来看匹配度。或者tid与变量绘图,看它搜索的位置收敛(非数学意义上的收敛)情况。
trials有这几种:
- trials.trials - a list of dictionaries representing everything about the search
- trials.results - a list of dictionaries returned by ‘objective’ during the search
- trials.losses() - a list of losses (float for each ‘ok’ trial) trials.statuses() - a list of status strings
5)优化算法
from hyperopt import fmin
MAX_EVALS = 500
# Optimize
best = fmin(fn = objective, space = space, algo = tpe.suggest,
max_evals = MAX_EVALS, trials = bayes_trials)使用sklearn的数据进行一次测试
#coding:utf-8
from hyperopt import fmin, tpe, hp, rand
import numpy as np
from sklearn.metrics import accuracy_score
from sklearn import svm
from sklearn import datasets
# SVM的三个超参数:C为惩罚因子,kernel为核函数类型,gamma为核函数的额外参数(对于不同类型的核函数有不同的含义)
# 有别于传统的网格搜索(GridSearch),这里只需要给出最优参数的概率分布即可,而不需要按照步长把具体的值给一个个枚举出来
parameter_space_svc ={
# loguniform表示该参数取对数后符合均匀分布
'C':hp.loguniform("C", np.log(1), np.log(100)),
'kernel':hp.choice('kernel',['rbf','poly']),
'gamma': hp.loguniform("gamma", np.log(0.001), np.log(0.1)),
}
# 鸢尾花卉数据集,是一类多重变量分析的数据集
# 通过花萼长度,花萼宽度,花瓣长度,花瓣宽度4个属性预测鸢尾花卉属于(Setosa,Versicolour,Virginica)三个种类中的哪一类
iris = datasets.load_digits()
#--------------------划分训练集和测试集--------------------
train_data = iris.data[0:1300]
train_target = iris.target[0:1300]
test_data = iris.data[1300:-1]
test_target = iris.target[1300:-1]
#-----------------------------------------------------------
# 计数器,每一次参数组合的枚举都会使它加1
count = 0
def function(args):
print(args)
# **可以把dict转换为关键字参数,可以大大简化复杂的函数调用
clf = svm.SVC(**args)
# 训练模型
clf.fit(train_data,train_target)
# 预测测试集
prediction = clf.predict(test_data)
global count
count = count + 1
score = accuracy_score(test_target,prediction)
print("第%s次,测试集正确率为:" % str(count),score)
# 由于hyperopt仅提供fmin接口,因此如果要求最大值,则需要取相反数
return -score
# algo指定搜索算法,目前支持以下算法:
# ①随机搜索(hyperopt.rand.suggest)
# ②模拟退火(hyperopt.anneal.suggest)
# ③TPE算法(hyperopt.tpe.suggest,算法全称为Tree-structured Parzen Estimator Approach)
# max_evals指定枚举次数上限,即使第max_evals次枚举仍未能确定全局最优解,也要结束搜索,返回目前搜索到的最优解
best = fmin(function, parameter_space_svc, algo=tpe.suggest, max_evals=100)
# best["kernel"]返回的是数组下标,因此需要把它还原回来
kernel_list = ['rbf','poly']
best["kernel"] = kernel_list[best["kernel"]]
print("最佳参数为:",best)
clf = svm.SVC(**best)
print(clf)输出结果如下:
{'gamma': 0.0010051585652497248, 'kernel': 'poly', 'C': 29.551164584073586}
第1次,测试集正确率为: 0.959677419355
{'gamma': 0.006498482991283678, 'kernel': 'rbf', 'C': 6.626826808981864}
第2次,测试集正确率为: 0.834677419355
{'gamma': 0.008192671915044216, 'kernel': 'poly', 'C': 34.48947180442318}
第3次,测试集正确率为: 0.959677419355
{'gamma': 0.001359874432712413, 'kernel': 'rbf', 'C': 1.6402360233244775}
第98次,测试集正确率为: 0.971774193548
{'gamma': 0.0029328466160223813, 'kernel': 'poly', 'C': 1.6328276445108112}
第99次,测试集正确率为: 0.959677419355
{'gamma': 0.0015786919481979775, 'kernel': 'rbf', 'C': 4.669133703622153}
第100次,测试集正确率为: 0.969758064516
最佳参数为: {'gamma': 0.00101162002595069, 'kernel': 'rbf', 'C': 21.12514792460218}
SVC(C=21.12514792460218, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape=None, degree=3, gamma=0.00101162002595069,
kernel='rbf', max_iter=-1, probability=False, random_state=None,
shrinking=True, tol=0.001, verbose=False)三、Optuna
有关这个库的文献好少,不过看代码的话,形式和Hyperopt差不太多
from sklearn.model_selection import train_test_split, cross_val_score, StratifiedKFold
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import roc_auc_score
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import numpy as np
import optuna
import os
from hyperopt import hp
# print(hp.loguniform('sdf',1,5))
# list_space = [
# hp.uniform('a', 0, 1),
# hp.loguniform('b', 0, 1)]
# tuple_space = (
# hp.uniform('a', 0, 1),
# hp.loguniform('b', 0, 1))
# dict_space = {
# 'a': hp.uniform('a', 0, 1),
# 'b': hp.loguniform('b', 0, 1)}
# print(dict_space,tuple_space,dict_space)
train=pd.read_csv('../data/train.csv', index_col='id')
test=pd.read_csv('../data/test.csv', index_col='id')
submission=pd.read_csv('../data/sample_submission.csv', index_col='id')
Ytrain=train['target']
train=train[list(test)]
all_data=pd.concat((train, test))
print(train.shape, test.shape, all_data.shape)
encoded=pd.get_dummies(all_data, columns=all_data.columns, sparse=True)
encoded=encoded.sparse.to_coo()
encoded=encoded.tocsr()
Xtrain=encoded[:len(train)]
Xtest=encoded[len(train):]
kf=StratifiedKFold(n_splits=10)
def objective(trial):
C=trial.suggest_loguniform('C', 10e-10, 10)
model=LogisticRegression(C=C, class_weight='balanced',max_iter=10000, solver='lbfgs', n_jobs=-1)
score=-cross_val_score(model, Xtrain, Ytrain, cv=kf, scoring='roc_auc').mean()
return score
study=optuna.create_study()
study.optimize(objective, n_trials=5)
print(study.best_params)
print(-study.best_value)
print(study.best_params)
model=LogisticRegression(C=0.09536298444122952, class_weight='balanced',max_iter=10000, solver='lbfgs', n_jobs=-1)
model.fit(Xtrain, Ytrain)
predictions=model.predict_proba(Xtest)[:,1]
submission['target']=predictions
submission.to_csv(r"E:\TensorFlow\大数据之路\kaggle\Categorical_Feature_Encoding_Challenge\result\res2.csv",
index=False)