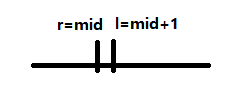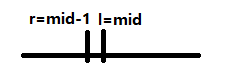算法思想
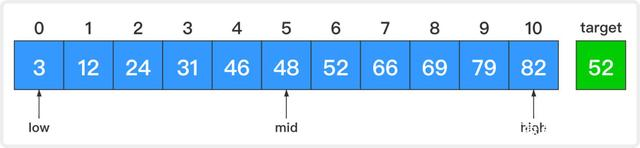
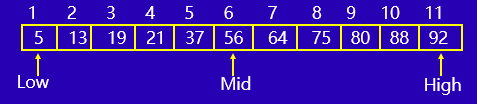
二分查找(折半查找) 是针对有序序列的一种快速查找方式,与高中时候数学中学的二分法有异曲同工之处。通过不断缩小目标值所在区间的范围实现快速查找到目标值。每次将目标值与区间内的中位数进行比较,比中位数小则在中位数的做区间内再查找,如果比中位数大则在中位数的有区间内再查找,以相同的规则作用于缩小后的区间,以此类推最终便可找到结果。
对于整数二分
单调性(有序序列)仅为二分查找的充分条件,而不是必要条件,即具有单调性的序列一定可以进行二分查找,而可以进行二分查找的数列不一定具有单调性,非单调性的数列也有可能可以进行二分查找。
假设某个区间被划分成两个具有不同性质的子区间,整数二分的本质就是可以分别找到两个子区间的左右边界,从而将两个不同性质的子区间划分出来。
参考文章:
二分查找又叫折半查找,是一种简单又快速的查找算法
取mid值的两种方式:
(1)向下取整 (2)向上取整
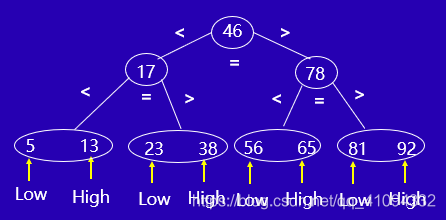
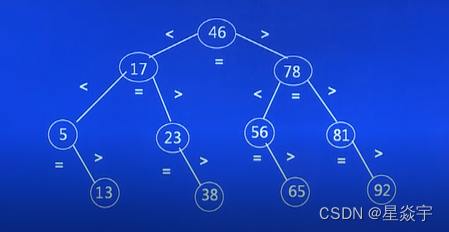
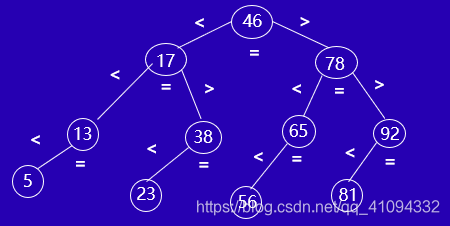
因为二分查找是以中点来进行左右分割,因此类比于二叉树,可以将中点作为树根,左右两侧作为左右子树,用二叉树的形式来进行表示。
(1)向下取整
由于二分查找的表为顺序表,因此向下取整的意义就是取表中下标较靠前的位置,同时也是两个数中较小的那个数。
(2)向上取整
取表中下标较靠后的位置,同时也是两个数中较大的那个数。
算法实现注意事项
(1)当 while循环 判定条件为 l <= r
循环内改变mid时,
若target在中位点左侧时,则说明目标在左侧区间,改变右边界的取值,缩小搜索目标到左区间内。
r = mid - 1;
同理,若target在中位点的右侧时,则说明目标在右侧区间,
l = mid + 1;
因l < = r所以左、右侧边界可以取到且可能会去到相同值。
(2)当 while循环 判定条件为 l < r (没有等号时)
在算法对整型数值进行二分查找中,主要是要考虑转换时的边界问题。
-
若选取的mid = (l + r) / 2 相当于向下取整,则需变换右边界时,应变为r = mid;当需变换左边界时,应变为l = mid + 1,最终将会得到靠左的位置l。
即可取到左侧边界,但不能取到右侧边界 [ ,)。 -
若选取的mid = (l + r + 1) / 2 相当于向上取整,则需变换左边界时,应变为l = mid;当需变换右边界时,应变为r = mid - 1,最终将会得到靠右的位置r。
即可渠道右侧边界,但不能取到左侧边界 ( , ]
算法模板
两步:获取中位数,和中位数对比
整型数二分
// l = 0, r = n
// x为带查找的数
int bsearch_1(int q[], int l, int r){
while(l < r){
int mid = l + (r - l) / 2;
// check():为判断q[mid]是否满足某种规定或性质
//if(check(q[mid])) r = mid;
// 假设此时的目标是寻找x,在左侧区间
if(q[mid] >= x) r = mid;
// 在右侧区间或等于q[mid] == x
else l = mid + 1;
}
return l;
}
// l = -1, r = n - 1
int bsearch_2(int q[], int l, int r){
while(l < r){
int mid = l + (r - l + 1) / 2;
//if(check(q[mid])) l = mid;
if(q[mid] <= x) l = mid;
else r = mid - 1;
}
return r;
}
int bsearch_3(int q[], int l, int r){
while (l <= r){
int mid = l + (r - l) / 2;
if(q[mid] <= x) l = mid + 1;
else r = mid - 1;
}
return r;
}
注:为防止l + r相加溢出,采取l + (r - l) / 2 结果等于 (r - l) / 2
* 新模板(统一区间取值)
int left_bound(int target){
int l = 0, r = n - 1;
while(l <= r){
int mid = l + (r - l) / 2;
if(nums[mid] == target){ // 往左侧压缩,更新右边界
r = mid - 1;
}else if(nums[mid] > target){
r = mid - 1;
}else if(nums[mid] < target){
l = mid + 1;
}
}
if(l >= n || target != nums[l]) return -1;
return l; // 注意返回值
}
int right_bound(int target){
int l = 0, r = n - 1;
while(l <= r){
int mid = l + (r - l) / 2;
if(nums[mid] == target){ // 往右侧压缩,更新左边界
l = mid + 1;
}else if(nums[mid] > target){
r = mid - 1;
}else if(nums[mid] < target){
l = mid + 1;
}
}
if(r < 0 || target != nums[r]) return -1;
return r; // 注意返回值
}
浮点型二分
double bsearch(int q[], int l, int r){
double eps = 1e-8; // 精度,一般比题中要求的再多两位
// l可为取值范围的左边界,r可为取值范围的有边界
while(max((l - r), 1) > 1e-8){
double mid = (l + r) / 2;
// 若目标x小于mid,则在左区间找;否则在有区间找
if(check(mid)) r = mid;
else l = mid;
}
return l;
}
- 时间复杂度O(log n)
- 空间复杂度O(1)
例题1:数的范围
给定一个按照升序排列的长度为 n 的整数数组,以及 q个查询。
对于每个查询,返回一个元素 k的起始位置和终止位置(位置从 0开始计数)。
如果数组中不存在该元素,则返回 -1 -1。
输入格式
第一行包含整数 n和 q,表示数组长度和询问个数。
第二行包含 n个整数(均在 1∼10000范围内),表示完整数组。
接下来 q行,每行包含一个整数 k,表示一个询问元素。
输出格式
共 q 行,每行包含两个整数,表示所求元素的起始位置和终止位置。
如果数组中不存在该元素,则返回 -1 -1。
数据范围
1≤n≤100000
1≤q≤10000
1≤k≤10000
输入样例
6 3
1 2 2 3 3 4
3
4
5
输出样例
3 4
5 5
-1 -1
算法实现
#include <stdio.h>
const int N = 1e5 + 10;
int main(){
int n, m; scanf("%d%d", &n, &m);
int q[N]; for(int i = 0; i < n; i++) scanf("%d", &q[i]);
while(m--){
int k; scanf("%d", &k);
// 先获取左下标值。左闭右开。
int i = 0, j = n - 1;
while(i < j){
int mid = i + j >> 1;
if(k <= q[mid]) j = mid;
else i = mid + 1;
}
if(k != q[j]) printf("-1 -1");
else{
printf("%d ", i);
// 再获取右下标值。左开右闭。
i = 0, j = n - 1;
while(i < j){
int mid = i + j + 1>> 1;
if(k >= q[mid]) i = mid;
else j = mid - 1;
}
printf("%d", i);
}
//puts("");
printf("\n");
}
return 0;
}
参考文章:
AcWing 789. 二分模板笔记
另一解法
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int n, q, k;
int nums[N];
int left_bound(int target){
int l = 0, r = n - 1;
while(l <= r){
int mid = l + (r - l) / 2;
if(nums[mid] == target){
r = mid - 1;
}else if(nums[mid] > target){
r = mid - 1;
}else if(nums[mid] < target){
l = mid + 1;
}
}
if(l >= n || target != nums[l]) return -1;
return l;
}
int right_bound(int target){
int l = 0, r = n - 1;
while(l <= r){
int mid = l + (r - l) / 2;
if(nums[mid] == target){
l = mid + 1;
}else if(nums[mid] > target){
r = mid - 1;
}else if(nums[mid] < target){
l = mid + 1;
}
}
if(r < 0 || target != nums[r]) return -1;
return r;
}
int main(){
cin >> n >> q;
int l, r;
for(int i = 0; i < n; i++) cin >> nums[i];
while(q--){
cin >> k;
l = left_bound(k);
if(l == -1) cout << "-1 -1" << endl;
else{
r = right_bound(k);
cout << l << " " << r << endl;
}
}
return 0;
}
例题2:查找某个数
Leetcode:704. 二分查找
例题3:插入搜索位置
注意返回值
例题4:在排序数组中查找元素的第一个和最后一个位置
分左右边界讨论,寻找左边界时,向左侧区间压缩;寻找右边界时,向右侧区间压缩。