机器学习里模型效果的好坏需要由特定的指标来评价,本文介绍在分类模型里常用的几种评价指标
1、 准确率、精确率、召回率、 F 1 F_1 F1-score
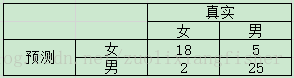
我们以分类算法为例,假设班里有50个同学,其中男生30个,女生20个,我们根据身高、体重、头发长度、声音分贝等等特征,想找到所有女生,比如已经有这样一个分类器了,得到结果如下:
这里我们是要找到所有女同学,故把女同学作为正样本(positive),男同学作为负样本(Negative),预测结果正确为True,预测结果错误为False。基于此,我们结合上面的数据给出如下定义和值:
- TP(True Positive): 真实是女生,预测结果也是女生的数量(18个)
- FN(False Negative): 真实是女生,预测结果是男生的数量(2个)
- TN(True Negative): 真实是男生,预测结果也是男生(25个)
- FP(False Postive): 真实是男生,预测结果是女生(5个)
| . | 相关(relevant),正类 | 无关(irrelevant),负类 |
|---|---|---|
| 被检索到(Retrieved) | true positives (TP 正类判定为正类, 例子中就是正确的判定"这位是女生") | false positives (FP 负类判定为正类,“存伪”, 例子中就是分明是男生却判断为女生, 当下伪娘横行, 这个错常有人犯) |
| 未被检索到(Not Retrieved) | false negatives (FN 正类判定为负类,“去真”, 例子中就是, 分明是女生, 这哥们却判断为男生–梁山伯同学犯的错就是这个) | true negatives (TN 负类判定为负类, 也就是一个男生被判断为男生, 像我这样的纯爷们一准儿就会在此处) |
有了这几个值,我们就可以计算准确率、精确率、召回率、
F
1
F_1
F1-score这几个值了
准确率(Accuracy): 衡量所有样本被分类准确的比例
A
c
c
u
r
a
c
y
=
T
P
+
T
N
T
P
+
F
P
+
T
N
+
F
N
Accuracy=\frac{TP+TN}{TP+FP+TN+FN}
Accuracy=TP+FP+TN+FNTP+TN
精确率(Precision): 也叫查准率,衡量正样本的分类准确率,就是说倍预测为正样本的样本有多少是真的正样本。
P
r
e
c
i
s
i
o
n
=
T
P
T
P
+
F
P
Precision=\frac{TP}{TP+FP}
Precision=TP+FPTP
召回率(Recall): 表示分类正确的正样本占总的正样本的比例
R
e
c
a
l
l
=
T
P
T
P
+
F
N
Recall=\frac{TP}{TP+FN}
Recall=TP+FNTP
F
1
F_1
F1-score: 精确率和召回率的调和平均
2
F
1
=
1
P
+
1
R
⟹
F
1
=
2
P
R
P
+
R
=
2
T
P
2
T
P
+
F
P
+
T
N
\frac{2}{F_1}=\frac{1}{P}+\frac{1}{R}\Longrightarrow F_1=\frac{2PR}{P+R}=\frac{2TP}{2TP+FP+TN}
F12=P1+R1⟹F1=P+R2PR=2TP+FP+TN2TP
可以看到,在上式里我们认为精确率和召回率是一样重要的(他们的权重一样),当我们的评估更加注重精确率或者召回率的时候,该怎么处理呢?
我们引入
F
β
F_{\beta}
Fβ,对于任意的非负值
β
\beta
β,我们定义
F
β
=
(
β
2
+
1
)
⋅
P
R
β
2
⋅
P
+
R
F_{\beta}=(\beta ^2+1)\cdot\frac{PR}{\beta^2\cdot P+R}
Fβ=(β2+1)⋅β2⋅P+RPR
可以看到,我们可以通过调整
β
\beta
β 来帮助我们更好地评估结果。
最好的分类器当然是准确率、精确率,召回率都为1,但实际场景中几乎是不可能的,而且精确率和召回率往往会相互影响,一个高了另一个会有所下降,因此在实际应用中要根据具体需求做适当平衡。
2、ROC、AUC
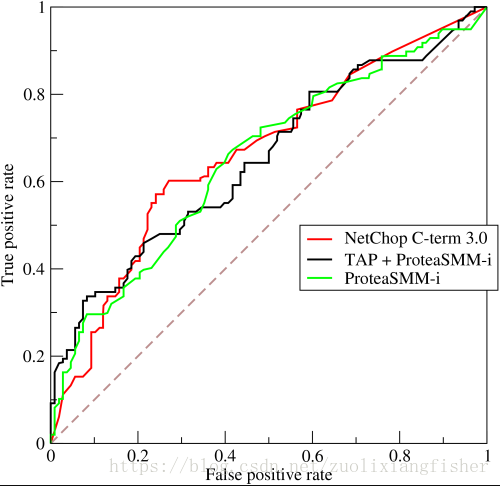
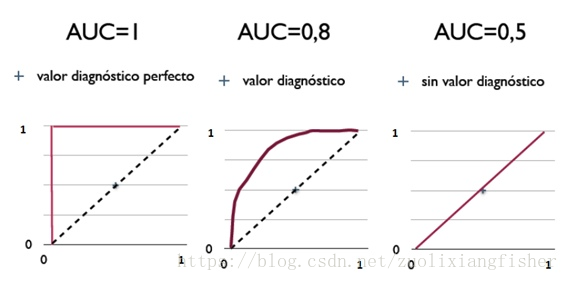
ROC(Receiver Operating Characteristic)曲线和AUC常被用来评价一个二值分类器(binary classifier)的优劣,下图就是ROC曲线的一个示意图
可以看到,ROC曲线横坐标是FPR(False Positive Rate),纵坐标是TPR(True Positive Rate)
F
P
R
=
F
P
F
P
+
T
N
,
T
P
R
=
T
P
T
P
+
F
N
FPR=\frac{FP}{FP+TN}, TPR=\frac{TP}{TP+FN}
FPR=FP+TNFP,TPR=TP+FNTP
接下来我们考虑ROC曲线图中的四个点和一条线。第一个点,(0,1),即FPR=0, TPR=1,这意味着FN(false negative)=0,并且FP(false positive)=0。Wow,这是一个完美的分类器,它将所有的样本都正确分类。第二个点,(1,0),即FPR=1,TPR=0,类似地分析可以发现这是一个最糟糕的分类器,因为它成功避开了所有的正确答案。第三个点,(0,0),即FPR=TPR=0,即FP(false positive)=TP(true positive)=0,可以发现该分类器预测所有的样本都为负样本(negative)。类似的,第四个点(1,1),分类器实际上预测所有的样本都为正样本。经过以上的分析,我们可以断言,ROC曲线越接近左上角,该分类器的性能越好。
2.1 如何画ROC曲线
对于一个特定的分类器和测试数据集,显然只能得到一组FPR和TPR结果,而要得到一个曲线,我们实际上需要一系列FPR和TPR的值,这又是如何得到的呢?我们先来看一下wikipedia上对ROC曲线的定义
A receiver operating characteristic curve, i.e. ROC curve, is a graphical plot that illustrates the diagnostic ability of a binary classifier system as its discrimination threshold is varied.
译:ROC曲线是由一系列因区分阈值变化产生的点,用于描述二分类模型的判断能力
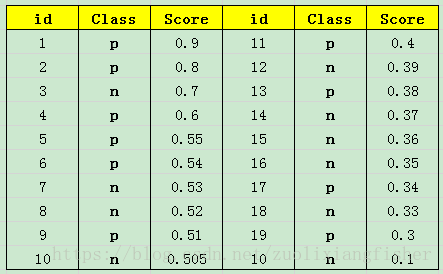
这里的关键在于 “its discrimination threshold is varied” ,因为对于一个二分类模型,它的输出结果其实是判断这个样本属于正样本的概率值,假如我们已经得到了所有样本的概率输出(属于正样本的概率),现在的问题是如何改变“discrimination threashold”?我们根据每个测试样本属于正样本的概率值从大到小排序。下图是一个示例,图中共有20个测试样本,“Class”一栏表示每个测试样本真正的标签(p表示正样本,n表示负样本),“Score”表示每个测试样本属于正样本的概率
然后我们按照样本的score值,从大到小依次作为阈值,当样本score值大于等于阈值时则判定为正样本,否则为负样本。
例如第一个阈值取0.9,这时只有id=1的样本被预测为正样本,其余都是负样本,此时TPR=1/1+9=0.1, FPR=0/0+10=0,
详细如下:
| threshold | TPR | FPR |
|---|---|---|
| 0.9 0.9 0.9 | 0.1 = 1 / ( 1 + 9 ) 0.1=1/(1+9) 0.1=1/(1+9) | 0 = 0 / ( 0 + 10 ) 0=0/(0+10) 0=0/(0+10) |
| 0.8 0.8 0.8 | 0.2 = 2 / ( 2 + 8 ) 0.2=2/(2+8) 0.2=2/(2+8) | 0 = 0 / ( 0 + 10 ) 0=0/(0+10) 0=0/(0+10) |
| 0.7 0.7 0.7 | 0.2 = 2 / ( 2 + 8 ) 0.2=2/(2+8) 0.2=2/(2+8) | 0.1 = 1 / ( 1 + 9 ) 0.1=1/(1+9) 0.1=1/(1+9) |
| 0.6 0.6 0.6 | 0.3 = 3 / ( 3 + 7 ) 0.3=3/(3+7) 0.3=3/(3+7) | 0.1 = 1 / ( 1 + 9 ) 0.1=1/(1+9) 0.1=1/(1+9) |
| 0.55 0.55 0.55 | 0.4 = 4 / ( 4 + 6 ) 0.4=4/(4+6) 0.4=4/(4+6) | 0.1 = 1 / ( 1 + 9 ) 0.1=1/(1+9) 0.1=1/(1+9) |
| 0.54 0.54 0.54 | 0.5 = 5 / ( 5 + 5 ) 0.5=5/(5+5) 0.5=5/(5+5) | 0.1 = 1 / ( 1 + 9 ) 0.1=1/(1+9) 0.1=1/(1+9) |
| 0.53 0.53 0.53 | 0.5 = 5 / ( 5 + 5 ) 0.5=5/(5+5) 0.5=5/(5+5) | 0.2 = 2 / ( 2 + 8 ) 0.2=2/(2+8) 0.2=2/(2+8) |
| 0.52 0.52 0.52 | 0.5 = 5 / ( 5 + 5 ) 0.5=5/(5+5) 0.5=5/(5+5) | 0.3 = 3 / ( 3 + 7 ) 0.3=3/(3+7) 0.3=3/(3+7) |
| 0.51 0.51 0.51 | 0.6 = 6 / ( 6 + 4 ) 0.6=6/(6+4) 0.6=6/(6+4) | 0.3 = 3 / ( 3 + 7 ) 0.3=3/(3+7) 0.3=3/(3+7) |
| 0.505 0.505 0.505 | 0.6 = 6 / ( 6 + 4 ) 0.6=6/(6+4) 0.6=6/(6+4) | 0.4 = 4 / ( 4 + 6 ) 0.4=4/(4+6) 0.4=4/(4+6) |
| 0.4 0.4 0.4 | 0.7 = 7 / ( 7 + 3 ) 0.7=7/(7+3) 0.7=7/(7+3) | 0.4 = 4 / ( 4 + 6 ) 0.4=4/(4+6) 0.4=4/(4+6) |
| 0.39 0.39 0.39 | 0.7 = 7 / ( 7 + 3 ) 0.7=7/(7+3) 0.7=7/(7+3) | 0.5 = 5 / ( 5 + 5 ) 0.5=5/(5+5) 0.5=5/(5+5) |
| 0.38 0.38 0.38 | 0.8 = 8 / ( 8 + 2 ) 0.8=8/(8+2) 0.8=8/(8+2) | 0.5 = 5 / ( 5 + 5 ) 0.5=5/(5+5) 0.5=5/(5+5) |
| 0.37 0.37 0.37 | 0.8 = 8 / ( 8 + 2 ) 0.8=8/(8+2) 0.8=8/(8+2) | 0.6 = 6 / ( 6 + 4 ) 0.6=6/(6+4) 0.6=6/(6+4) |
| 0.36 0.36 0.36 | 0.8 = 8 / ( 8 + 2 ) 0.8=8/(8+2) 0.8=8/(8+2) | 0.7 = 7 / ( 7 + 3 ) 0.7=7/(7+3) 0.7=7/(7+3) |
| 0.35 0.35 0.35 | 0.8 = 8 / ( 8 + 2 ) 0.8=8/(8+2) 0.8=8/(8+2) | 0.8 = 8 / ( 8 + 2 ) 0.8=8/(8+2) 0.8=8/(8+2) |
| 0.34 0.34 0.34 | 0.9 = 9 / ( 9 + 1 ) 0.9=9/(9+1) 0.9=9/(9+1) | 0.8 = 8 / ( 8 + 2 ) 0.8=8/(8+2) 0.8=8/(8+2) |
| 0.33 0.33 0.33 | 0.9 = 9 / ( 9 + 1 ) 0.9=9/(9+1) 0.9=9/(9+1) | 0.9 = 9 / ( 9 + 1 ) 0.9=9/(9+1) 0.9=9/(9+1) |
| 0.3 0.3 0.3 | 1 = 10 / ( 10 + 0 ) 1=10/(10+0) 1=10/(10+0) | 0.9 = 9 / ( 9 + 1 ) 0.9=9/(9+1) 0.9=9/(9+1) |
| 0.1 0.1 0.1 | 1 = 10 / ( 10 + 0 ) 1=10/(10+0) 1=10/(10+0) | 1 = 10 / ( 10 + 0 ) 1=10/(10+0) 1=10/(10+0) |
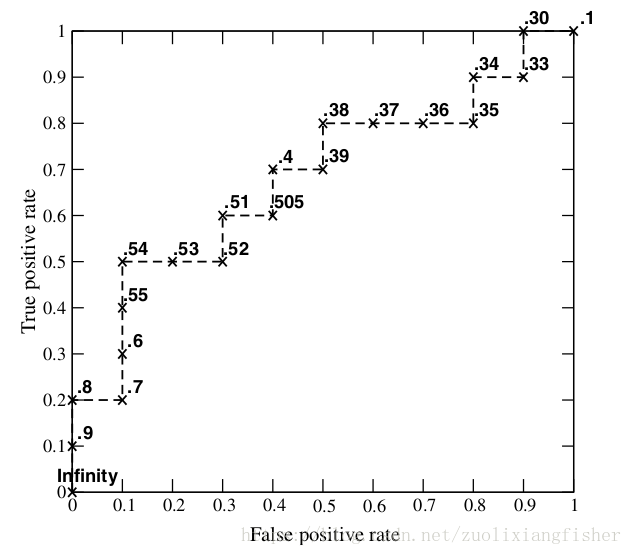
由此我们便得到了一组(FPR,TPR)的值,可以绘制出ROC曲线
当我们将threshold设置为1和0时,分别可以得到ROC曲线上的(0,0)和(1,1)两个点。将这些(FPR,TPR)对连接起来,就得到了ROC曲线。当threshold取值越多,ROC曲线越平滑。
2.2 计算AUC值
AUC(Area Under Curve)被定义为ROC曲线下的面积,显然这个面积的数值不会大于1。又由于ROC曲线一般都处于y=x这条直线的上方,所以AUC的取值范围在0.5和1之间。使用AUC值作为评价标准是因为很多时候ROC曲线并不能清晰的说明哪个分类器的效果更好,而作为一个数值,对应AUC更大的分类器效果更好。
The AUC value is equivalent to the probability that a randomly chosen positive example is ranked higher than a randomly chosen negative example.
可以看到AUC应该理解为对随机取出一个正样本和一个负样本,模型预测正样本为正样本的概率大于预测负样本为正样本的概率的概率值。
可能不太好理解这句话,那我们还是用上面的例子来说明,假设二分类模型A要找到所有正样本,对20个样本的预测概率根据概率值大小得到一个排序,我们希望有尽可能多的正样本排在负样本前面,最好的模型当然是所有的正样本都排在负样本前,但这种分类器要不就是过拟合要不就不存在,当有越多正样本排在负样本前的时候,我们得到的ROC曲线上的点的分布会越靠近y轴(FPR=0)和y=1(TPR=1)这两条线,显然这时候曲线下的面积值(AUC) 会越接近于1,这个时候我们再看上面对AUC的理解这句话,随机取出一个正样本和一个负样本,
如果auc值大,当然会有更多的正样本被更大概率预测准确,负样本被预测为正样本的概率也会越小。
2.3 为什么要用ROC曲线
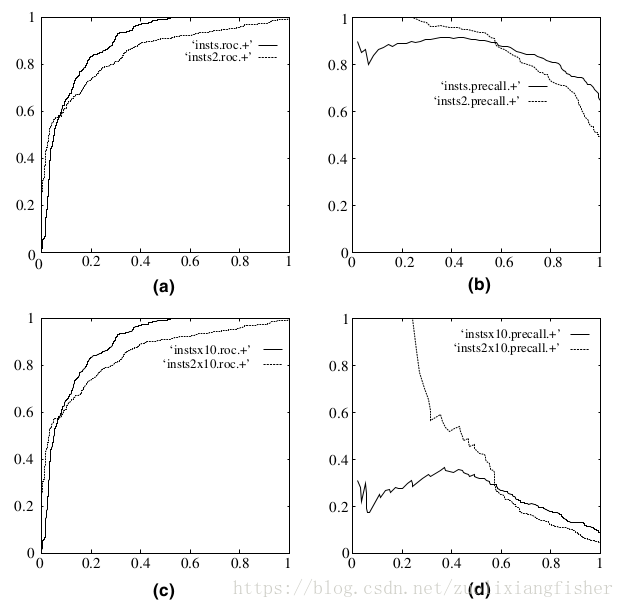
既然已经这么多评价标准,为什么还要使用ROC和AUC呢?因为ROC曲线有个很好的特性:当测试集中的正负样本的分布变化的时候,ROC曲线能够保持不变。在实际的数据集中经常会出现类不平衡(class imbalance)现象,即负样本比正样本多很多(或者相反),而且测试数据中的正负样本的分布也可能随着时间变化。下图是ROC曲线和Precision-Recall曲线的对比:
在上图中,(a)和©为ROC曲线,(b)和(d)为Precision-Recall曲线。(a)和(b)展示的是分类其在原始测试集(正负样本分布平衡)的结果,©和(d)是将测试集中负样本的数量增加到原来的10倍后,分类器的结果。可以明显的看出,ROC曲线基本保持原貌,而Precision-Recall曲线则变化较大。
参考资料:
1、https://en.wikipedia.org/wiki/Receiver_operating_characteristic
2、https://www.jianshu.com/p/c61ae11cc5f6