前言
本文目的
介绍一些常见的用于图像加密的评价指标并予以代码实现,方便以后做实验时参考查阅。
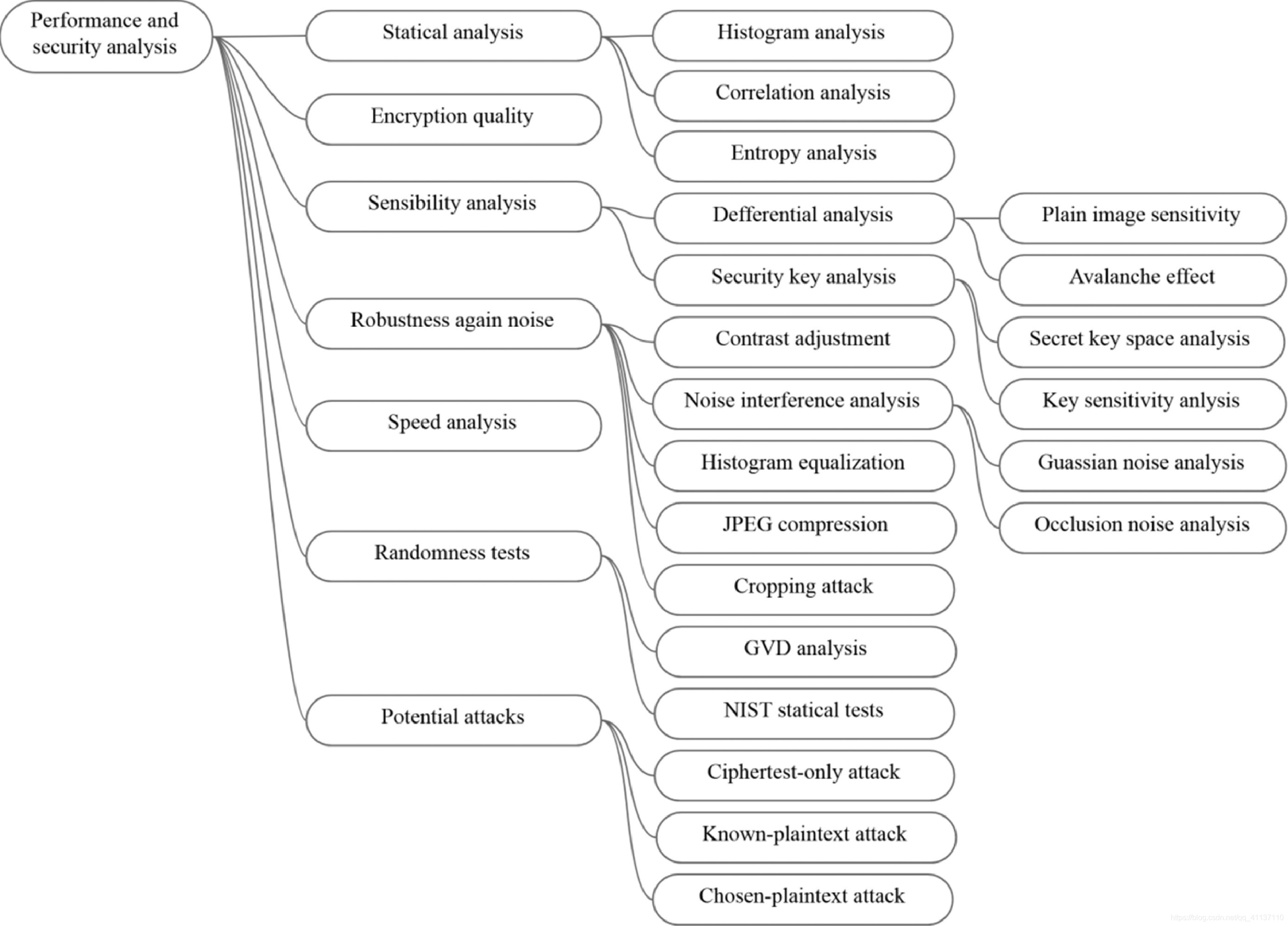
图像加密领域所有常见的安全分析技术汇总如下图。
实验示例图片下载
Lena.png,Lena_encrypt1.png,Lena_encrypt2.png
注:Lena.png为原图像,Lena_encrypt1.png、Lena_encrypt2.png为使用不同密钥加密的图像。
加密过程参见【使用基于混沌理论和SHA-2的异或与DNA互补规则的彩色图像加密技术】
灵敏度分析
密钥空间分析
密钥空间指能够用于生成密钥的所有可能密钥的集合,密钥空间的大小取决于安全密钥的长度,它是决定密码系统强度的最重要特性之一。对于长度为 L 的二进制安全密钥,其密钥空间大小为2 𝐿,即攻击者想要通过暴力攻击的手 段攻击加密系统,理论上需要计算2𝐿次才能保证一定能攻击成功。以现阶段计 算机的计算能力来看,当安全密钥长度 L = 128, 即密钥空间大小为 2 128 2^{128} 2128时,使用现代高性能计算机检查所有可能的密钥需要大约 1021 年,因此,加密算法能抵御任何形式的暴力攻击。
密钥敏感性分析
概念
理想的多媒体加密应该对密钥敏感,即密钥中一个比特的变化应该产生一个完全不同的加密结果,称为密钥敏感性。一般来说,混沌密码的密钥灵敏度是指混沌映射的初始状态的灵敏度和控制参数的灵敏度。灵敏度的评估使用两个参数:像素数变化率(NPCR)和统一平均变化强度(UACI)。NPCR和UACI分别表示两张加密图像之间的变化像素数和两张加密图像之间的平均变化强度数。它们相应的理想值分别为 NPCR=99.6094%,UACI=33.4635%,计算公式如下:
N
P
C
R
=
Σ
i
,
j
D
(
i
,
j
)
M
∗
N
∗
100
%
NPCR=\frac{\Sigma_{i,j}D(i,j)}{M*N}*100\%
NPCR=M∗NΣi,jD(i,j)∗100%
式中,M和N分别为两幅随机图像的宽度和高度,定义D (i, j)如下:
D
(
i
,
j
)
=
f
(
x
)
=
{
1
,
C
1
(
i
,
j
)
≠
C
2
(
i
,
j
)
0
,
o
t
h
e
r
w
i
s
e
\begin{array}{lr} D(i,j)=f(x)=\left\{ \begin{array}{lr} 1,\ C_1(i,j)\neq C_2(i,j) \\ 0,\ otherwise \\ \end{array} \right . \end{array}
D(i,j)=f(x)={1, C1(i,j)=C2(i,j)0, otherwise
相应地,UACI可以用来测量颜色分量对比度强度的平均值,计算公式如下:
U
A
C
I
=
1
M
∗
N
Σ
(
C
1
(
i
,
j
)
−
C
2
(
i
,
j
)
)
255
∗
100
%
UACI=\frac{1}{M*N}\frac{\Sigma(C_1(i,j)-C_2(i,j))}{255}*100\%
UACI=M∗N1255Σ(C1(i,j)−C2(i,j))∗100%
密钥敏感度测试可以通过修改密钥 K 中的某一位得到 K’,利用 K 和 K’ 加密同一张图像得到
C
1
C_1
C1和
C
2
C_2
C2,采用像素改变率 NPCR 和像素平均改变强度 UACI 量化两张密文图像的差别。NPCR 和 UACI 越接近理想值,加密算法对安全密钥 的敏感度越强,加密算法越安全。
实验结果
| PSNR | UACI | |
|---|---|---|
| R | 99.5686% | 33.4380% |
| G | 99.6098% | 33.4592% |
| B | 99.6178% | 33.4337% |
实验代码
import cv2
import numpy as np
import matplotlib.pyplot as plt
'''
计算像素数变化率
'''
def NPCR(img1,img2):
#opencv颜色通道顺序为BGR
img1=cv2.imread(img1)
img2=cv2.imread(img2)
w,h,_=img1.shape
#图像通道拆分
B1,G1,R1=cv2.split(img1)
B2,G2,R2=cv2.split(img2)
#返回数组的排序后的唯一元素和每个元素重复的次数
ar,num=np.unique((R1!=R2),return_counts=True)
R_npcr=(num[0] if ar[0]==True else num[1])/(w*h)
ar,num=np.unique((G1!=G2),return_counts=True)
G_npcr=(num[0] if ar[0]==True else num[1])/(w*h)
ar,num=np.unique((B1!=B2),return_counts=True)
B_npcr=(num[0] if ar[0]==True else num[1])/(w*h)
return R_npcr,G_npcr,B_npcr
'''
两张图像之间的平均变化强度
'''
def UACI(img1,img2):
img1=cv2.imread(img1)
img2=cv2.imread(img2)
w,h,_=img1.shape
#图像通道拆分
B1,G1,R1=cv2.split(img1)
B2,G2,R2=cv2.split(img2)
#元素为uint8类型取值范围:0到255
# print(R1.dtype)
#强制转换元素类型,为了运算
R1=R1.astype(np.int16)
R2=R2.astype(np.int16)
G1=G1.astype(np.int16)
G2=G2.astype(np.int16)
B1=B1.astype(np.int16)
B2=B2.astype(np.int16)
sumR=np.sum(abs(R1-R2))
sumG=np.sum(abs(G1-G2))
sumB=np.sum(abs(B1-B2))
R_uaci=sumR/255/(w*h)
G_uaci=sumG/255/(w*h)
B_uaci=sumB/255/(w*h)
return R_uaci,G_uaci,B_uaci
def main():
#img='./lena.png'
img1='./lena_encrypt1.png'
img2='./lena_encrypt2.png'
R_npcr,G_npcr,B_npcr=NPCR(img1,img2)
print('*********PSNR*********')
#百分数表示,保留小数点后4位
print('Red :{:.4%}'.format(R_npcr))
print('Green:{:.4%}'.format(G_npcr))
print('Blue :{:.4%}'.format(B_npcr))
R_uaci,G_uaci,B_uaci=UACI(img1,img2)
print('*********UACI*********')
#百分数表示,保留小数点后4位
print('Red :{:.4%}'.format(R_uaci))
print('Green:{:.4%}'.format(G_uaci))
print('Blue :{:.4%}'.format(B_uaci))
if __name__== '__main__':
main()
差分攻击
破解密文图像的一种方法是差分攻击:它指的是攻击者对原始明文数字图像数据进行细微的改变,利用提出的加密算法对改变后的数字图像和原始明文数字图像分别进行加密,并通过比较两幅加密后的密文图像,找出原始明文数字图像数据与加密后密文数字图像数据之间的关系,利用这种关系和规律来进行对密文图像进行破解。通俗点说,它是指攻击者对大小为M × N的图像P做少量改动得到 P’,分别利用相同的安全密钥加密P和P’得到 C1 和C2 ,比较 C1和 C2的区别以找到攻击图像加密方案的线索。当 C1和 C2表现出较大差异时,攻击者就难以实施差分攻击。差分攻击是一种选择明文攻击,抗差分攻击性能依赖于对明文的敏感性,在图像加密领域,衡量两张图像的差异有两个非常重要的变量:像素改变率 (NPCR)和统一平均变化强度(UACI)。像素改变率NPCR反映了两张图像相同位置不相等的像素的个数占图像所有像素个数的比例;UACI 是整体平均变化密度,表示平面图像的平均变化的强度,主要体现普通明文数字图像数据和加密后的密文数字图像数据之间的差异的平均变化的强弱程度。为了抵抗差分攻击,在明文图像发生一个像素变化时,要使密文图像有大幅度的变化,则抵抗差分攻击的能力越强。 NPCR和UACI的理想值分别为99.6094%和33.4635%,当某算法的NPCR和UACI计算结果越接近于理想值时,则说明该算法抵抗差分攻击的能力越强。
统计分析
直方图分析
概念
直方图显示图像的统计信息,直观地反映了图像中各个灰度值的分布情况。明文图像的直方图表现出明显的统计规律,针对统计规律的攻击方案被称为统计分析攻击。统计分析攻击是指攻击者通过分析密文和明文的统计规律来破译密码。攻击者对截获 的密文图像进行统计分析,总结出其间的统计规律,并与明文的统计规律进行 比较,从中提取明文图像和密文图像之间的变换关系, 以达到攻击加密方案的目的。为了抵抗统计攻击,加密图像的直方图必须是均匀的,并且完全不同于明文图像的直方图。直方图的方差能有效量化加密算法抵御统计分析攻击能力。方差越小,说明像素 分布越均匀,图像显示的统计信息就越少,图像加密方案就越安全。
实验结果
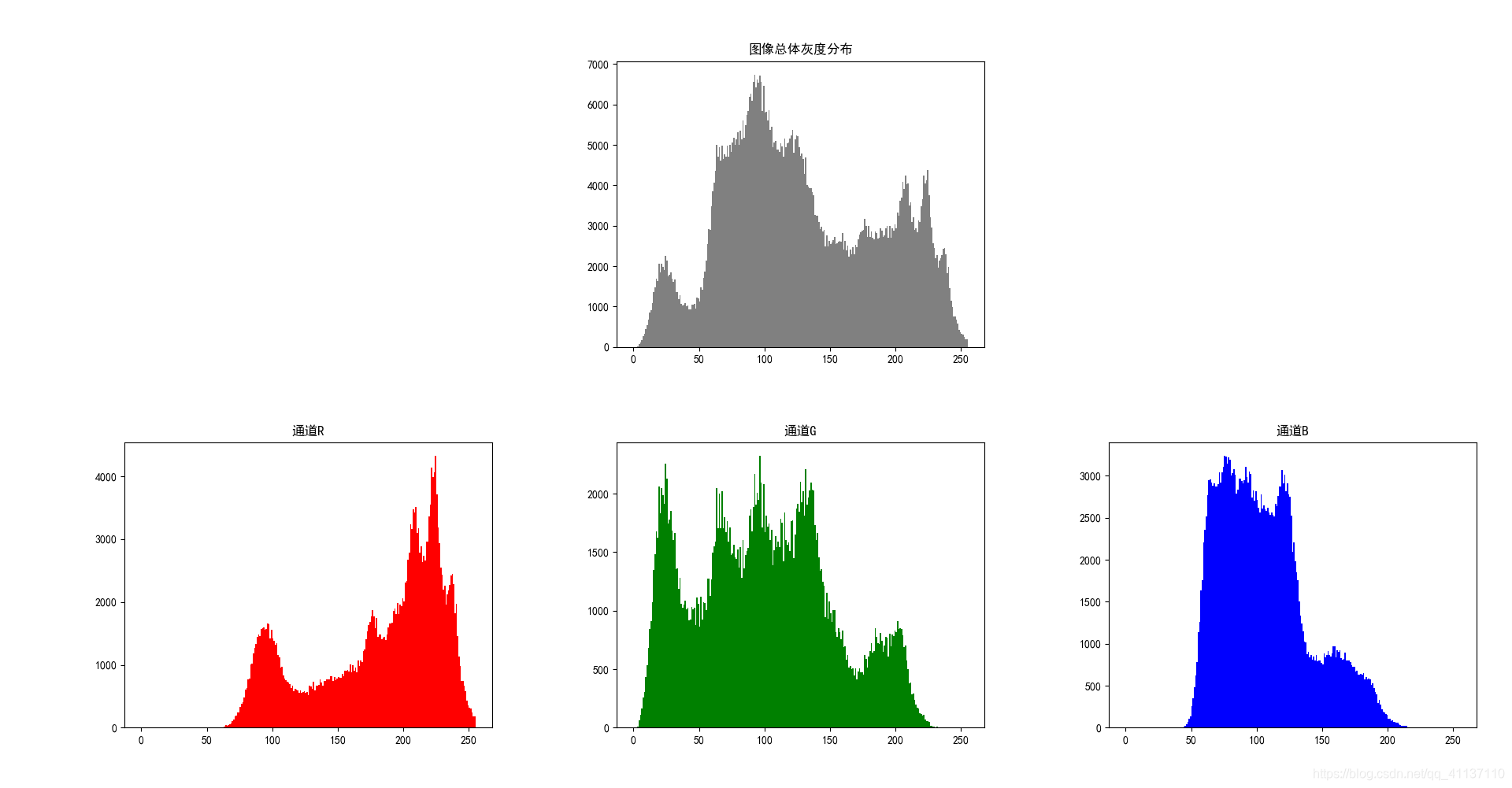
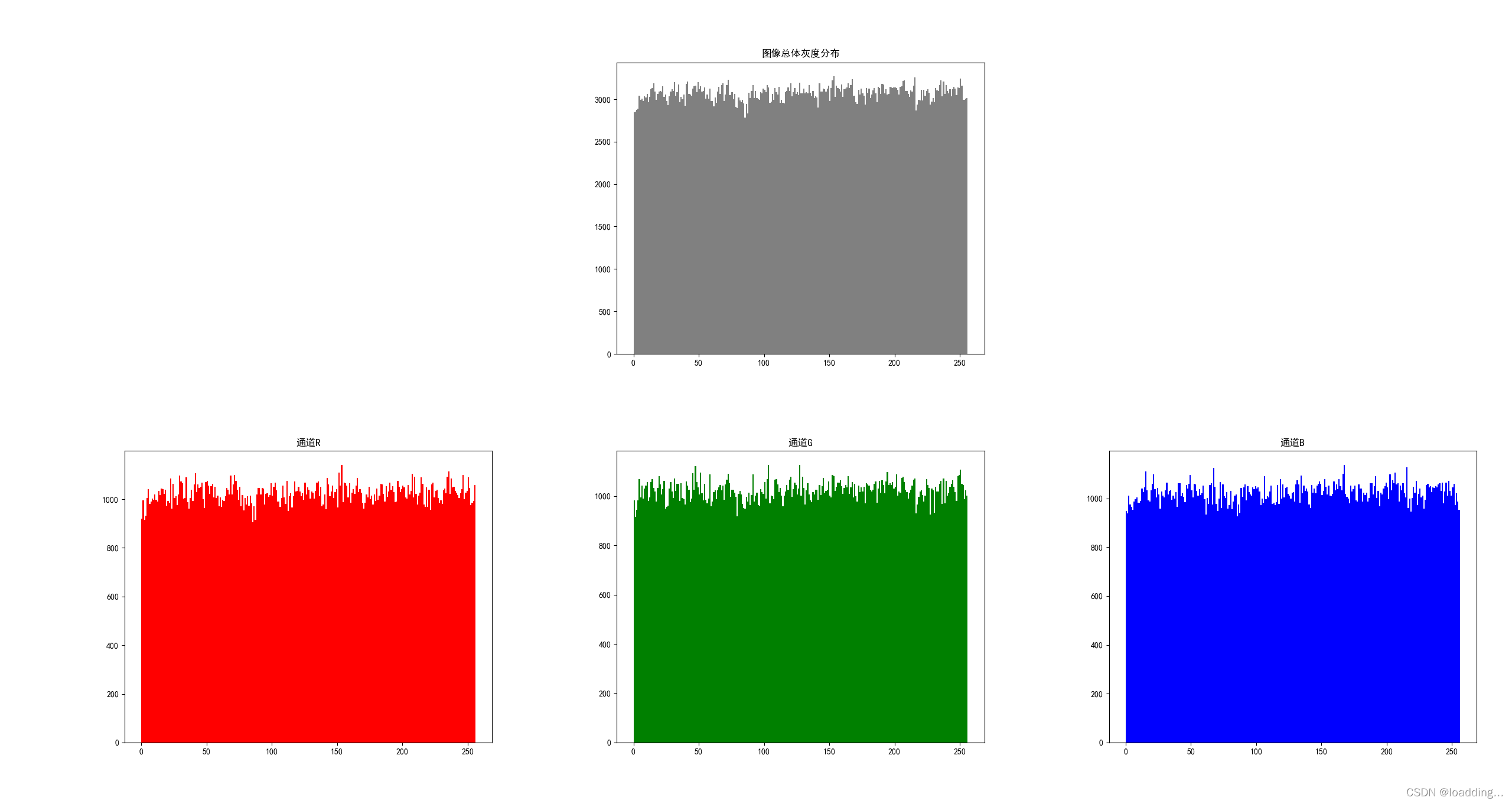
原图像Lena.png的灰度直方图如下:
加密图像Lena_encrypt1.png的灰度直方图如下:
实验代码
import cv2
import numpy as np
import matplotlib.pyplot as plt
'''
绘制灰度直方图
'''
def hist(img):
img=cv2.imread(img)
B,G,R=cv2.split(img)
#转成一维
R=R.flatten(order='C')
G=G.flatten(order='C')
B=B.flatten(order='C')
#结果展示
plt.rcParams['font.sans-serif'] = ['SimHei'] # 中文乱码
plt.subplot(232)
# plt.imshow(img[:,:,(2,1,0)])
plt.hist(img.flatten(order='C'),bins=range(257),color='gray')
plt.title('原图像')
#子图2,通道R
plt.subplot(234)
#imshow()对图像进行处理,画出图像,show()进行图像显示
plt.hist(R,bins=range(257),color='red')
plt.title('通道R')
# plt.show()
#不显示坐标轴
# plt.axis('off')
#子图3,通道G
plt.subplot(235)
plt.hist(G,bins=range(257),color='green')
plt.title('通道G')
# plt.show()
# plt.axis('off')
#子图4,通道B
plt.subplot(236)
plt.hist(B,bins=range(257),color='blue')
plt.title('通道B')
# plt.axis('off')
# #设置子图默认的间距
plt.tight_layout()
plt.show()
def main():
img='./lena.png'
#图像lean的灰度直方图
hist(img)
if __name__== '__main__':
main()
相邻像素相关性分析
概念
相关性分析是指对两个或多个具备相关性的变量元素进行分析,从而衡量变量之间的相关密切程度。由于图像相邻像素之间存在着很高的相关性,一个像素往往会泄露其周边像素的信息,攻击者往往可以利用该特性推理预测出下一个像素的灰度值,,从而实现对整个明文图像的恢复。数字图像中的相邻像素具有相似的强度;因此具有很强的相关性,这些强相关性必须被打破,以避免统计攻击。相关系数在水平、垂直和对角线方向的计算公式如下:
R
x
y
=
c
o
v
(
x
,
y
)
D
(
x
)
D
(
y
)
R_{xy}=\frac{cov(x,y)}{\sqrt{D(x)}\sqrt{D(y)}}
Rxy=D(x)D(y)cov(x,y)
E ( x ) = 1 N ∑ i = 1 N x i E(x)=\frac{1}{N}\sum_{i=1}^{N}{x_i} E(x)=N1i=1∑Nxi
D ( x ) = 1 N ∑ i = 1 N ( x i − E ( x ) ) 2 D(x)=\frac{1}{N}\sum_{i=1}^{N}{(x_i-E(x))^2} D(x)=N1i=1∑N(xi−E(x))2
c
o
v
(
x
,
y
)
=
1
N
∑
i
=
1
N
(
x
i
−
E
(
x
)
)
(
y
i
−
E
(
y
)
)
cov(x,y)=\frac{1}{N}\sum_{i=1}^{N}{(x_i-E(x))(y_i-E(y))}
cov(x,y)=N1i=1∑N(xi−E(x))(yi−E(y))
上述式子中,y为x的相邻像素,N为M × N幅图像中像素的总数,
R
x
y
R_{xy}
Rxy即为两相邻像素的相关性,cov(x, y)是x和y两个像素点处的协方差,
D
(
x
)
\sqrt{D(x)}
D(x)是标准差,D(x)是方差,E(x)是均值。通常,明文图像相邻像素的相关性接近 1,而密文图像相邻像素的相关性应该接近于 0。
实验结果
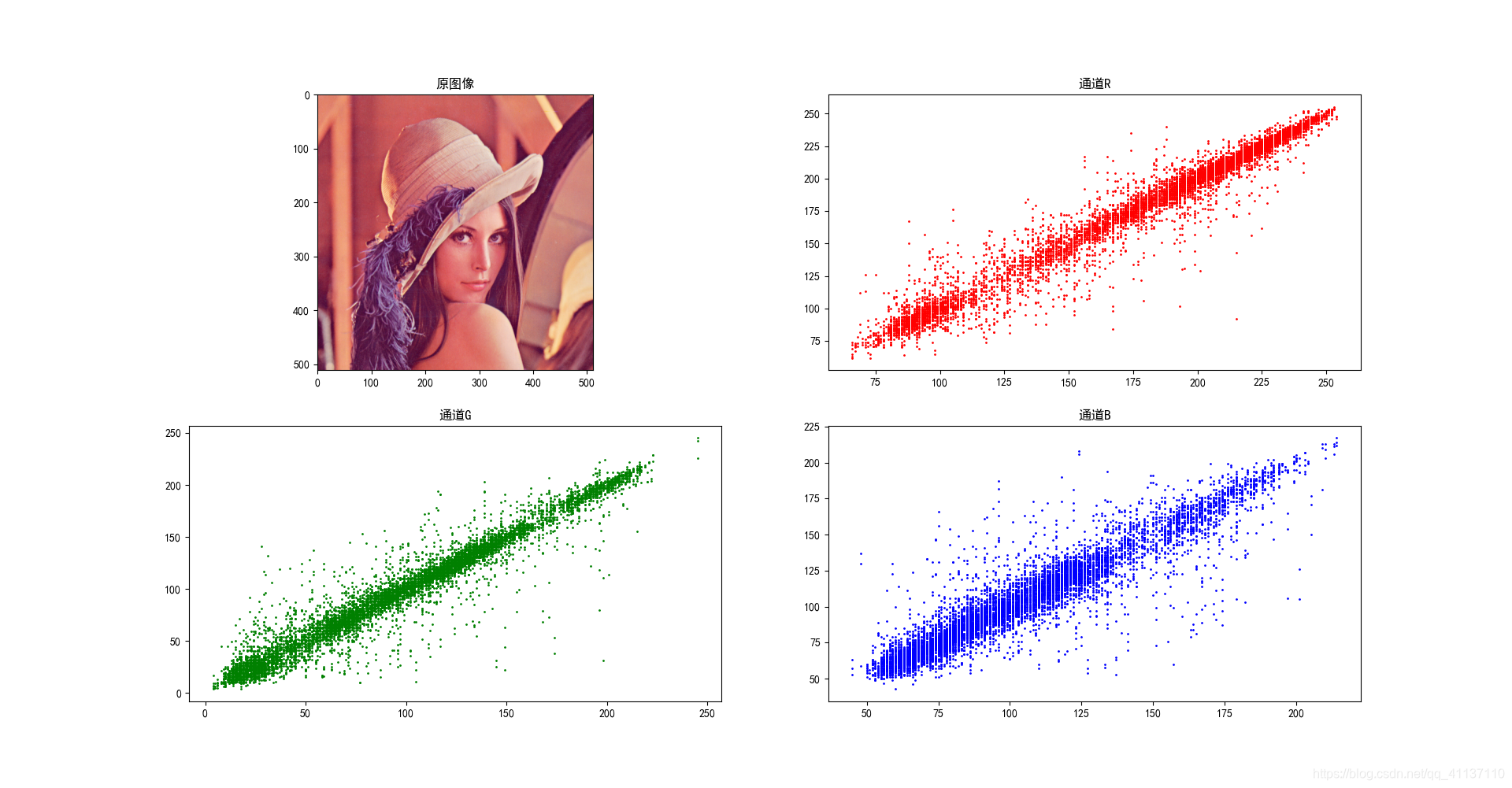
通过分别随机选取3000对相邻像素,根据相关系数的上述定义在水平、垂直和对角方向分别计算原图像和加密图像内的相关系数,实验结果如下:
原Lena图像的相关系数
| 通道 | Horizontal | Vertical | Diagonal |
|---|---|---|---|
| R | 0.9782 | 0.9893 | 0.9664 |
| G | 0.9699 | 0.9805 | 0.9548 |
| B | 0.9359 | 0.9572 | 0.9239 |
加密图像1的相关系数
| 通道 | Horizontal | Vertical | Diagonal |
|---|---|---|---|
| R | -0.0110 | -0.0091 | 0.0223 |
| G | -0.0260 | -0.0175 | -0.0228 |
| B | -0.0147 | -0.0078 | -0.0114 |
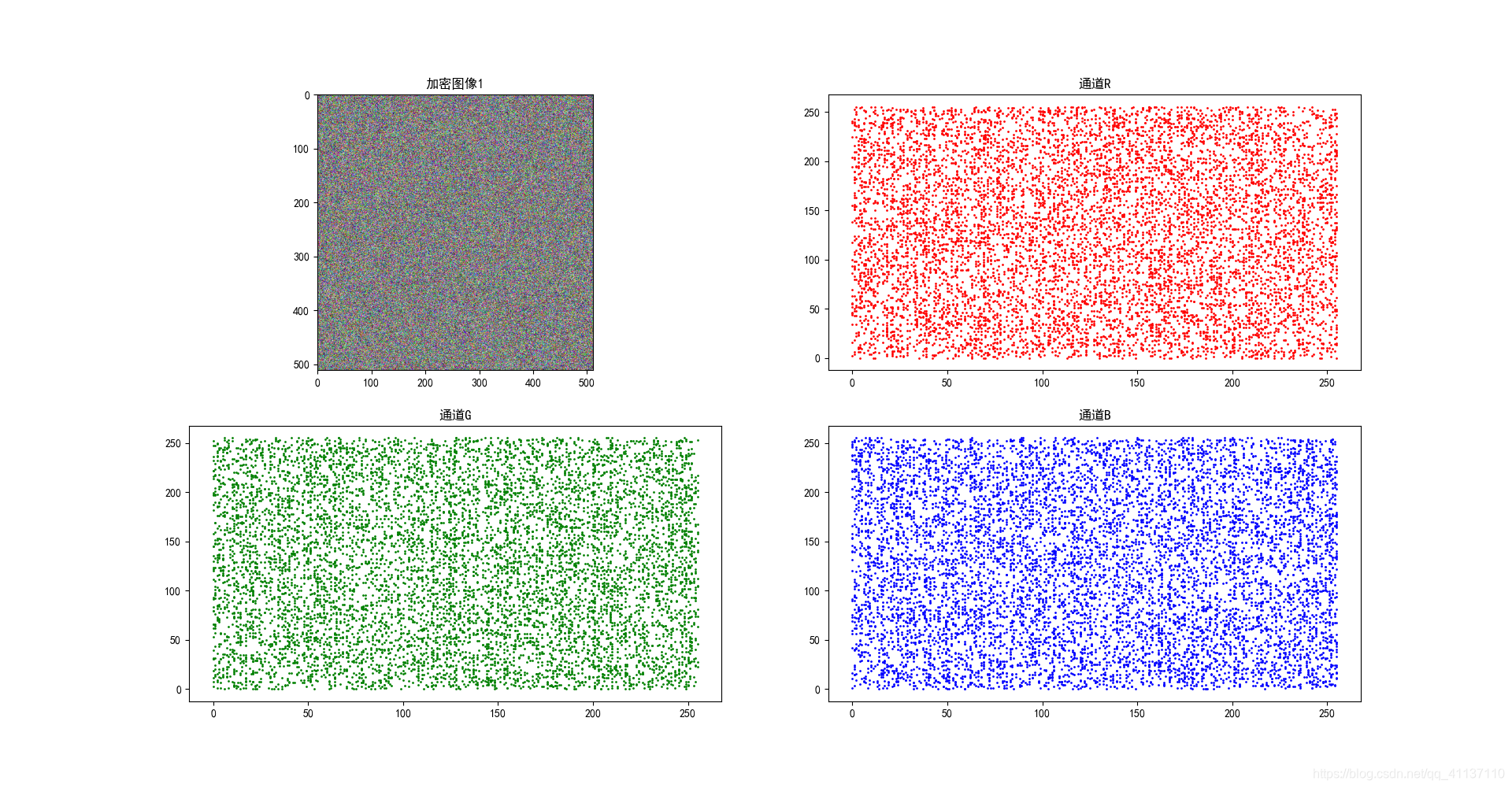
原始图像像素相关性图
加密图像1像素相关性图
实验代码
import cv2
import numpy as np
import matplotlib.pyplot as plt
'''
分别计算图像通道相邻像素的水平、垂直和对角线的相关系数并返回
'''
def RGB_correlation(channel,N):
#计算channel通道
h,w=channel.shape
#随机产生pixels个[0,w-1)范围内的整数序列
row=np.random.randint(0,h-1,N)
col=np.random.randint(0,w-1,N)
#绘制相邻像素相关性图,统计x,y坐标
x=[]
h_y=[]
v_y=[]
d_y=[]
for i in range(N):
#选择当前一个像素
x.append(channel[row[i]][col[i]])
#水平相邻像素是它的右侧也就是同行下一列的像素
h_y.append(channel[row[i]][col[i]+1])
#垂直相邻像素是它的下方也就是同列下一行的像素
v_y.append(channel[row[i]+1][col[i]])
#对角线相邻像素是它的右下即下一行下一列的那个像素
d_y.append(channel[row[i]+1][col[i]+1])
#三个方向的合到一起
x=x*3
y=h_y+v_y+d_y
#结果展示
# plt.rcParams['font.sans-serif'] = ['SimHei'] # 中文乱码
# plt.scatter(x,y)
# plt.show()
#计算E(x),计算三个方向相关性时,x没有重新选择也可以更改
ex=0
for i in range(N):
ex+=channel[row[i]][col[i]]
ex=ex/N
#计算D(x)
dx=0
for i in range(N):
dx+=(channel[row[i]][col[i]]-ex)**2
dx/=N
#水平相邻像素h_y
#计算E(y)
h_ey=0
for i in range(N):
h_ey+=channel[row[i]][col[i]+1]
h_ey/=N
#计算D(y)
h_dy=0
for i in range(N):
h_dy+=(channel[row[i]][col[i]+1]-h_ey)**2
h_dy/=N
#计算协方差
h_cov=0
for i in range(N):
h_cov+=(channel[row[i]][col[i]]-ex)*(channel[row[i]][col[i]+1]-h_ey)
h_cov/=N
h_Rxy=h_cov/(np.sqrt(dx)*np.sqrt(h_dy))
#垂直相邻像素v_y
#计算E(y)
v_ey=0
for i in range(N):
v_ey+=channel[row[i]+1][col[i]]
v_ey/=N
#计算D(y)
v_dy=0
for i in range(N):
v_dy+=(channel[row[i]+1][col[i]]-v_ey)**2
v_dy/=N
#计算协方差
v_cov=0
for i in range(N):
v_cov+=(channel[row[i]][col[i]]-ex)*(channel[row[i]+1][col[i]]-v_ey)
v_cov/=N
v_Rxy=v_cov/(np.sqrt(dx)*np.sqrt(v_dy))
#对角线相邻像素d_y
#计算E(y)
d_ey=0
for i in range(N):
d_ey+=channel[row[i]+1][col[i]+1]
d_ey/=N
#计算D(y)
d_dy=0
for i in range(N):
d_dy+=(channel[row[i]+1][col[i]+1]-d_ey)**2
d_dy/=N
#计算协方差
d_cov=0
for i in range(N):
d_cov+=(channel[row[i]][col[i]]-ex)*(channel[row[i]+1][col[i]+1]-d_ey)
d_cov/=N
d_Rxy=d_cov/(np.sqrt(dx)*np.sqrt(d_dy))
return h_Rxy,v_Rxy,d_Rxy,x,y
'''
分别计算图像img的各通道相邻像素的相关系数,默认随机选取3000对相邻像素
'''
def correlation(img,N=3000):
img=cv2.imread(img)
h,w,_=img.shape
B,G,R=cv2.split(img)
R_Rxy=RGB_correlation(R,N)
G_Rxy=RGB_correlation(G,N)
B_Rxy=RGB_correlation(B,N)
#结果展示
plt.rcParams['font.sans-serif'] = ['SimHei'] # 中文乱码
plt.subplot(221)
plt.imshow(img[:,:,(2,1,0)])
plt.title('原图像')
#子图2
plt.subplot(222)
plt.scatter(R_Rxy[3],R_Rxy[4],s=1,c='red')
plt.title('通道R')
#子图3
plt.subplot(223)
plt.scatter(G_Rxy[3],G_Rxy[4],s=1,c='green')
plt.title('通道G')
#子图4
plt.subplot(224)
plt.scatter(B_Rxy[3],B_Rxy[4],s=1,c='blue')
plt.title('通道B')
plt.show()
return R_Rxy[0:3],G_Rxy[0:3],B_Rxy[0:3]
def main():
img='./lena.png'
img1='./lena_encrypt1.png'
img2='./lena_encrypt2.png'
R_Rxy,G_Rxy,B_Rxy=correlation(img)
#输出结果保留四位有效数字
print("******该图像的各通道各方向的相关系数为*****")
print('通道\tHorizontal\tVertical\tDiagonal')
print(' R \t{:.4f} {:.4f} {:.4f}'.format(R_Rxy[0],R_Rxy[1],R_Rxy[2]))
print(' G \t{:.4f} {:.4f} {:.4f}'.format(G_Rxy[0],G_Rxy[1],G_Rxy[2]))
print(' B \t{:.4f} {:.4f} {:.4f}'.format(B_Rxy[0],B_Rxy[1],B_Rxy[2]))
if __name__== '__main__':
main()
信息熵分析
概念
熵常用来描述事物的复杂性,信源的信息熵是度量信息随机性的一个重要 参考指标。信息论之父克劳德·香农给出的信息熵的三个性质:单调性,发生 概率越高的事件其携带的信息量越低;非负性,信息熵作为一种广度量,非负 性是一种合理的必然;累加性,多随机事件同时发生存在的总不确定性的量度是可以表示为各事件不确定性的量度之和。
信息熵是对信号源随机程度的一种定量度量。也就是说,信息熵可以用来衡量图像的随机性,它计算每个颜色通道的每个灰度级的像素的扩散。如果均匀分布更好,那么它对统计攻击的抵抗就会更强。对于彩色图像强度在0-255之间的R、G、B通道,加密消息的理想熵值为8,值越高,分布越均匀。
信息熵计算公式如下:
H
(
x
)
=
−
∑
i
=
1
L
P
(
x
i
)
log
2
P
(
x
i
)
H(x)=-\sum_{i=1}^{L}{P(x_i)\log_{2}{P(x_i)}}
H(x)=−i=1∑LP(xi)log2P(xi)
其中,
x
i
x_i
xi是灰度值,
P
(
x
i
)
P(x_i)
P(xi)是灰度级
x
i
x_i
xi的概率。
实验结果
| 信息熵计算 | 原Lena图像 | 加密图像1 | 加密图像2 |
|---|---|---|---|
| R | 6.879 | 7.999 | 7.999 |
| G | 6.926 | 7.999 | 7.999 |
| B | 6.968 | 7.999 | 7.999 |
实验代码
import cv2
import math
import numpy as np
import matplotlib.pyplot as plt
'''
计算图像的信息熵
'''
def entropy(img):
img=cv2.imread(img)
w,h,_=img.shape
B,G,R=cv2.split(img)
gray,num1=np.unique(R,return_counts=True)
gray,num2=np.unique(G,return_counts=True)
gray,num3=np.unique(B,return_counts=True)
R_entropy=0
G_entropy=0
B_entropy=0
for i in range(len(gray)):
p1=num1[i]/(w*h)
p2=num2[i]/(w*h)
p3=num3[i]/(w*h)
R_entropy-=p1*(math.log(p1,2))
G_entropy-=p2*(math.log(p2,2))
B_entropy-=p3*(math.log(p3,2))
return R_entropy,G_entropy,B_entropy
def main():
img='./lena.png'
img1='./lena_encrypt1.png'
img2='./lena_encrypt2.png'
#图像lena的熵
R_entropy,G_entropy,B_entropy=entropy(img)
print('***********信息熵*********')
print('通道R:{:.4}'.format(R_entropy))
print('通道G:{:.4}'.format(G_entropy))
print('通道B:{:.4}'.format(B_entropy))
if __name__== '__main__':
main()
随机性测试
GVD
概念
灰度差度是比较原始图像和加密图像的随机性的另一种统计度量,可由下式定义:
KaTeX parse error: No such environment: equation at position 8: \begin{̲e̲q̲u̲a̲t̲i̲o̲n̲}̲ GN(x,y)=\frac…
其中G(x, y)表示位置(x, y)处的灰度值。整幅图像的平均邻域灰度差可以用下式子计算:
G
V
D
=
A
N
′
[
G
N
(
x
,
y
)
]
−
A
N
[
G
N
(
x
,
y
)
]
A
N
′
[
G
N
(
x
,
y
)
]
+
A
N
[
G
N
(
x
,
y
)
]
GVD=\frac{AN'[GN(x,y)]-AN[GN(x,y)]}{AN'[GN(x,y)]+AN[GN(x,y)]}
GVD=AN′[GN(x,y)]+AN[GN(x,y)]AN′[GN(x,y)]−AN[GN(x,y)]
A N [ G N ( x , y ) ] = ∑ x = 2 M − 1 ∑ y = 2 N − 1 G N ( x , y ) ( M − 2 ) ( N − 2 ) AN[GN(x,y)]=\frac{\sum_{x=2}^{M-1}{\sum_{y=2}^{N-1}{GN(x,y)}}}{(M-2)(N-2)} AN[GN(x,y)]=(M−2)(N−2)∑x=2M−1∑y=2N−1GN(x,y)
在上两个式子中,AN和AN’代表平均邻域灰度值,但前者表示加密前,后者表示加密后。上述方程的最终结果称为GVD评分,如果两幅图像完全相同,则为0,否则为1。
实验结果
| GVD | 原图-加密图像1 | 原图-加密图像2 |
|---|---|---|
| R | 0.9864 | 0.9864 |
| G | 0.9753 | 0.9754 |
| B | 0.9768 | 0.9768 |
实验代码
import cv2
import math
import numpy as np
import matplotlib.pyplot as plt
#计算图像分量的GVD,参数为加密前后的2个分量二维矩阵
def GVD_components(channel0,channel1):
AN0=0
AN1=0
w,h=channel0.shape
for i in range(1,w-1):
for j in range(1,h-1):
#加密前
GN0=0
GN0+=(channel0[i][j]-channel0[i-1][j])**2
GN0+=(channel0[i][j]-channel0[i+1][j])**2
GN0+=(channel0[i][j]-channel0[i][j-1])**2
GN0+=(channel0[i][j]-channel0[i][j+1])**2
GN0/=4
#加密后
GN1=0
GN1+=(channel1[i][j]-channel1[i-1][j])**2
GN1+=(channel1[i][j]-channel1[i+1][j])**2
GN1+=(channel1[i][j]-channel1[i][j-1])**2
GN1+=(channel1[i][j]-channel1[i][j+1])**2
GN1/=4
AN0+=GN0
AN1+=GN1
AN0/=((w-2)*(h-2))
AN1/=((w-2)*(h-2))
gvd=(AN1-AN0)/(AN1+AN0)
return gvd
def GVD(img1,img2):
img1=cv2.imread(img1)
img2=cv2.imread(img2)
w,h,_=img1.shape
B1,G1,R1=cv2.split(img1)
B2,G2,R2=cv2.split(img2)
R1=R1.astype(np.int16)
R2=R2.astype(np.int16)
G1=G1.astype(np.int16)
G2=G2.astype(np.int16)
B1=B1.astype(np.int16)
B2=B2.astype(np.int16)
R_gvd=GVD_components(R1,R2)
G_gvd=GVD_components(G1,G2)
B_gvd=GVD_components(B1,B2)
return R_gvd,G_gvd,B_gvd
def main():
img='./lena.png'
img1='./lena_encrypt1.png'
img2='./lena_encrypt2.png'
#计算GVD
R_gvd,G_gvd,B_gvd=GVD(img,img1)
print('***********GVD*********')
#print(R_gvd,G_gvd,B_gvd)
print('通道R:{:.4}'.format(R_gvd))
print('通道G:{:.4}'.format(G_gvd))
print('通道B:{:.4}'.format(B_gvd))
if __name__== '__main__':
main()
加密质量
概念
图像加密的质量可由下式决定:
E
Q
=
∑
L
=
0
255
(
H
L
(
E
)
−
H
L
(
I
)
)
2
/
256
EQ=\sum_{L=0}^{255}{(H_L(E)-H_L(I))^2/256}
EQ=L=0∑255(HL(E)−HL(I))2/256
其中
E
(
i
,
j
)
E(i,j)
E(i,j)和
I
(
i
,
j
)
I(i,j)
I(i,j)分别是M*N像素L灰度级的密文和明文图像在(i,j)处的像素灰度值。很显然,
I
(
i
,
j
)
、
E
(
i
,
j
)
∈
{
0
,
1
,
.
.
,
L
−
1
}
I(i,j)、E(i,j)\in \{0,1,..,L-1\}
I(i,j)、E(i,j)∈{0,1,..,L−1}。将
H
L
(
I
)
H_L(I)
HL(I) 和
H
L
(
E
)
H_L(E)
HL(E)定义为每个灰度级L各自在明文图像和密码图像中的出现次数,EQ表示每个灰度级l的平均变化次数,EQ值越大,加密安全性越好。
实验结果
注:512*512图像,EQ值最大应该是1024???待考虑??
| EQ | 原图-加密图像1 | 原图-加密图像2 |
|---|---|---|
| R | 807 | 804 |
| G | 589 | 590 |
| B | 1027 | 1027 |
实验代码
import cv2
import math
import numpy as np
import matplotlib.pyplot as plt
'''
计算加密质量,img1是原图,img2是加密图像
'''
def EQ(img1,img2):
img1=cv2.imread(img1)
img2=cv2.imread(img2)
w,h,_=img1.shape
B1,G1,R1=cv2.split(img1)
B2,G2,R2=cv2.split(img2)
R1_H={}
R2_H={}
G1_H={}
G2_H={}
B1_H={}
B2_H={}
R_EQ=0
G_EQ=0
B_EQ=0
for i in range(256):
R1_H[i]=0
R2_H[i]=0
G1_H[i]=0
G2_H[i]=0
B1_H[i]=0
B2_H[i]=0
for i in range(w):
for j in range(h):
R1_H[R1[i][j]]+=1;
R2_H[R2[i][j]]+=1;
G1_H[G1[i][j]]+=1;
G2_H[G2[i][j]]+=1;
B1_H[B1[i][j]]+=1;
B2_H[B2[i][j]]+=1;
for i in range(256):
#公式里是平方,待考虑
R_EQ+=abs(R1_H[i]-R2_H[i])
G_EQ+=abs(G1_H[i]-G2_H[i])
B_EQ+=abs(B1_H[i]-B2_H[i])
# print(R_EQ)
R_EQ/=256
G_EQ/=256
B_EQ/=256
return R_EQ,G_EQ,B_EQ
def main():
img='./lena.png'
img1='./lena_encrypt1.png'
img2='./lena_encrypt2.png'
#计算加密质量
R_EQ,G_EQ,B_EQ=EQ(img,img1)
print('***********EQ*********')
print(R_EQ,G_EQ,B_EQ)
print('通道R:{:.0f}'.format(R_EQ))
print('通道G:{:.0f}'.format(G_EQ))
print('通道B:{:.0f}'.format(B_EQ))
if __name__== '__main__':
main()
鲁棒性分析
噪声攻击(Noise addition)
概念
在现实世界中,图像在互联网上的传输不可避免地会受到各种因素的影响,比如噪声,通信噪声造成的失真、退化和污染是很常见的,这些因素都会对终端图像的解密产生一定的影响,从有噪声的密文 中恢复图像是比较困难的。因此,图像加密算法必须具有足够的鲁棒性,以抵抗实际场景中的噪声攻击。在仿真实验中,大多数的研究人员常会对密文图像添加不同程度的高斯噪声或椒盐噪声进行实验,再对有噪声的加密图像进行解密并对解密结果进行比较。抗噪声能力是测试加密方案性能的一个重要指标。
实验结果
对加密图像1分别添加均值为零,方差为0.0005的高斯噪声和5%的校验噪声,然后进行解密,结果如下
实验代码
import cv2
import math
import random
import numpy as np
import matplotlib.pyplot as plt
def gauss_noise(image, mean=0, var=0.001):
'''
添加高斯噪声
mean : 均值
var : 方差
'''
image = np.array(image/255, dtype=float)
noise = np.random.normal(mean, var ** 0.5, image.shape)
out = image + noise
if out.min() < 0:
low_clip = -1.
else:
low_clip = 0.
out = np.clip(out, low_clip, 1.0)
out = np.uint8(out*255)
return out
#默认10%的椒盐噪声
def salt_and_pepper_noise(noise_img, proportion=0.1):
height, width, _ = noise_img.shape
num = int(height * width * proportion) # 多少个像素点添加椒盐噪声
for i in range(num):
w = random.randint(0, width - 1)
h = random.randint(0, height - 1)
if random.randint(0, 1) == 0:
noise_img[h, w] = 0
else:
noise_img[h, w] = 255
return noise_img
def main():
img='./lena.png'
img1='./lena_encrypt1.png'
img2='./lena_encrypt2.png'
im=cv2.imread(img1)
gauss_img=gauss_noise(im,mean=0,var=0.0005)
salt_img=salt_and_pepper_noise(im,proportion=0.05)
cv2.imwrite('./gauss_img.png',gauss_img)
cv2.imwrite('./salt_img.png',salt_img)
if __name__== '__main__':
main()
阻塞攻击
概念
在互联网上的通信过程中,图像的一部分可能丢失,提出的算法必须能够以适当的方式处理有损图像的解码。为了显示所提出的密码在这种情况下的强度,分别从一个图形中去掉红色通道的一块像素、绿色通道的一块像素以及所有通道的一块像素,然后对它们进行解密;如果解密后原始信息被保留,并且原始图像的内容可以可视化,所提出的密码将能够处理有损图像的解密。
实验结果
从加密图像1中移除(换成0)一块80×80像素的红色通道,一块50×80像素的绿色通道和一块60×50像素的全通道,然后进行解密,结果如图。
实验代码
import cv2
import math
import numpy as np
import matplotlib.pyplot as plt
'''
对加密图像进行处理,返回处理后的结果
'''
def occlusion(img):
img=cv2.imread(img)
h,w,_=img.shape
B,G,R=cv2.split(img)
#随机移除R通道80*80大小的像素
#产生随机整数,裁剪大小为80
pos_w=np.random.randint(0,w-80)
pos_h=np.random.randint(0,h-80)
for i in range(80):
for j in range(80):
R[pos_h+i][pos_w+j]=0
#随机移除G通道50*80的像素
pos_w=np.random.randint(0,w-50)
pos_h=np.random.randint(0,h-80)
for i in range(80):
for j in range(50):
G[pos_h+i][pos_w+j]=0
#三通道合并
im=cv2.merge([R,G,B])
#随机移除All通道60*50的像素
pos_w=np.random.randint(0,w-60)
pos_h=np.random.randint(0,h-50)
for i in range(50):
for j in range(60):
im[pos_h+i][pos_w+j]=np.array([0,0,0])
return im
def main():
img='./lena.png'
img1='./lena_encrypt1.png'
img2='./lena_encrypt2.png'
lossy_encrypt=occlusion(img1)
# plt.imshow(lossy_encrypt)
# plt.show()
#保存处理后的有损加密图像,opencv的颜色通道顺序为[B,G,R]
cv2.imwrite('./Lossy_Lena_encrypt1.png',lossy_encrypt[:,:,(2,1,0)])
if __name__== '__main__':
main()
裁剪攻击
当在互联网上通信时,图像的一部分可能会被裁剪甚至丢失,因此提出的密码必须能够以适当的方式处理有损图像的加密。在仿真实验中,将密文图像的一部分区域(例如,该区域占总区域的1%、5%和10%)像素设置为0,然后用正确的密钥对其解密。在图像处理中,可以通过分析密文图像和明文图像之间的峰值信噪比(PSNR)来判断重构图像的质量,裁剪处理参见上面阻塞攻击,PSNR计算参见下面。
峰值信噪比(PSNR)
概念
峰值信噪比主要考察对应像素点之间的误差。给定大小为M*N的加密图像X和原图像Y,均方误差(MSE)定义为:
M
S
E
=
1
M
∗
N
∑
i
=
1
M
∑
j
=
1
N
(
X
(
i
,
j
)
−
Y
(
i
,
j
)
)
2
MSE=\frac{1}{M*N}\sum_{i=1}^{M}\sum_{j=1}^{N}{(X(i,j)-Y(i,j))^2}
MSE=M∗N1i=1∑Mj=1∑N(X(i,j)−Y(i,j))2
PSNR计算公式如下:
P
S
N
R
=
10
log
10
(
2
n
−
1
)
2
M
S
E
PSNR=10\log_{10}{\frac{(2^n-1)^2}{MSE}}
PSNR=10log10MSE(2n−1)2
其中,M、N分别表示图像的宽高,n为像素位数;PSNR值越大,表示失真越小,两张图片差距越小,加密效果越差。
实验结果
| PSNR | 原图-加密图像1 | 原图-加密图像2 |
|---|---|---|
| R | 7.895 | 7.890 |
| G | 8.562 | 8.548 |
| B | 9.603 | 9.612 |
实验代码
import cv2
import math
import numpy as np
import matplotlib.pyplot as plt
def PSNR(img1,img2):
img1=cv2.imread(img1)
img2=cv2.imread(img2)
w,h,_=img1.shape
B1,G1,R1=cv2.split(img1)
B2,G2,R2=cv2.split(img2)
#强制转换元素类型,为了运算
R1=R1.astype(np.int32)
R2=R2.astype(np.int32)
G1=G1.astype(np.int32)
G2=G2.astype(np.int32)
B1=B1.astype(np.int32)
B2=B2.astype(np.int32)
#计算均方误差,初始化64位无符号整型,防止累加中溢出
R_mse=np.uint64(0)
G_mse=np.uint64(0)
B_mse=np.uint64(0)
for i in range(w):
for j in range(h):
R_mse+=(R1[i][j]-R2[i][j])**2
G_mse+=(G1[i][j]-G2[i][j])**2
B_mse+=(B1[i][j]-B2[i][j])**2
R_mse/=(w*h)
G_mse/=(w*h)
B_mse/=(w*h)
R_psnr=10*math.log((255**2)/R_mse,10)
G_psnr=10*math.log((255**2)/G_mse,10)
B_psnr=10*math.log((255**2)/B_mse,10)
return R_psnr,G_psnr,B_psnr
def main():
img='./lena.png'
img1='./lena_encrypt1.png'
img2='./lena_encrypt2.png'
#计算PSNR
R_psnr,G_psnr,B_psnr=PSNR(img,img1)
print('***********峰值信噪比*********')
print(R_psnr,G_psnr,B_psnr)
print('通道R:{:.4}'.format(R_psnr))
print('通道G:{:.4}'.format(G_psnr))
print('通道B:{:.4}'.format(B_psnr))
if __name__== '__main__':
main()
对比度调节
一幅图像中必须存在合适的亮度和对比度,这样才能让人看得舒服,前者代表整个图像的明度或暗度,后者定义亮度的差异,以确定不同区域的清晰分离。因此,对比度调整是一种图像处理机制,其中的输入强度映射到所需的水平,以增强感兴趣的区域或区域。
时间和空间开销分析
加密算法的时间和空间开销是衡量加密算法性能的重要指标之一。时间开销分析通常包括加/解密算法的时间复杂度分析和模拟平台测试的真实的加/解密运行速度,通过对算法的时间复杂度的分析从理论上证明图像加密算法在效率上的可行性。空间开销分析是指分析图像加密算法在加/解密过程中占用的最大内存单元,给出模拟平台下需要的最大内存资源。一个好的加密算法应该尽可能地花费较少的时间成本,并占用较少的空间资源。
潜在攻击
纯密文攻击
概念
在只有密文本身可用的情况下解密密文的一种攻击,攻击者试图恢复相应的明文或加密密钥。
已知明文攻击
概念
攻击者试图在拥有密文和相关的纯文本片段的情况下恢复密钥。
选择明文攻击
概念
一种具有优异扩散特性的图像加密算法,能够抵抗选择明文攻击。然而,当几种现有的图像加密算法使用相同的安全密钥加密原始图像时,它们的加密图像是重复的。攻击者利用这个安全弱点,使用选定的纯文本攻击来破坏加密算法
未完待续。。。。
参考
【An overview of encryption algorithms in color images】
【A color image encryption technique using exclusive-OR with DNA complementary rules based on chaos theory and SHA-2】