我的LeetCode代码仓：https://github.com/617076674/LeetCode

原题链接：https://leetcode-cn.com/problems/largest-rectangle-in-histogram/description/

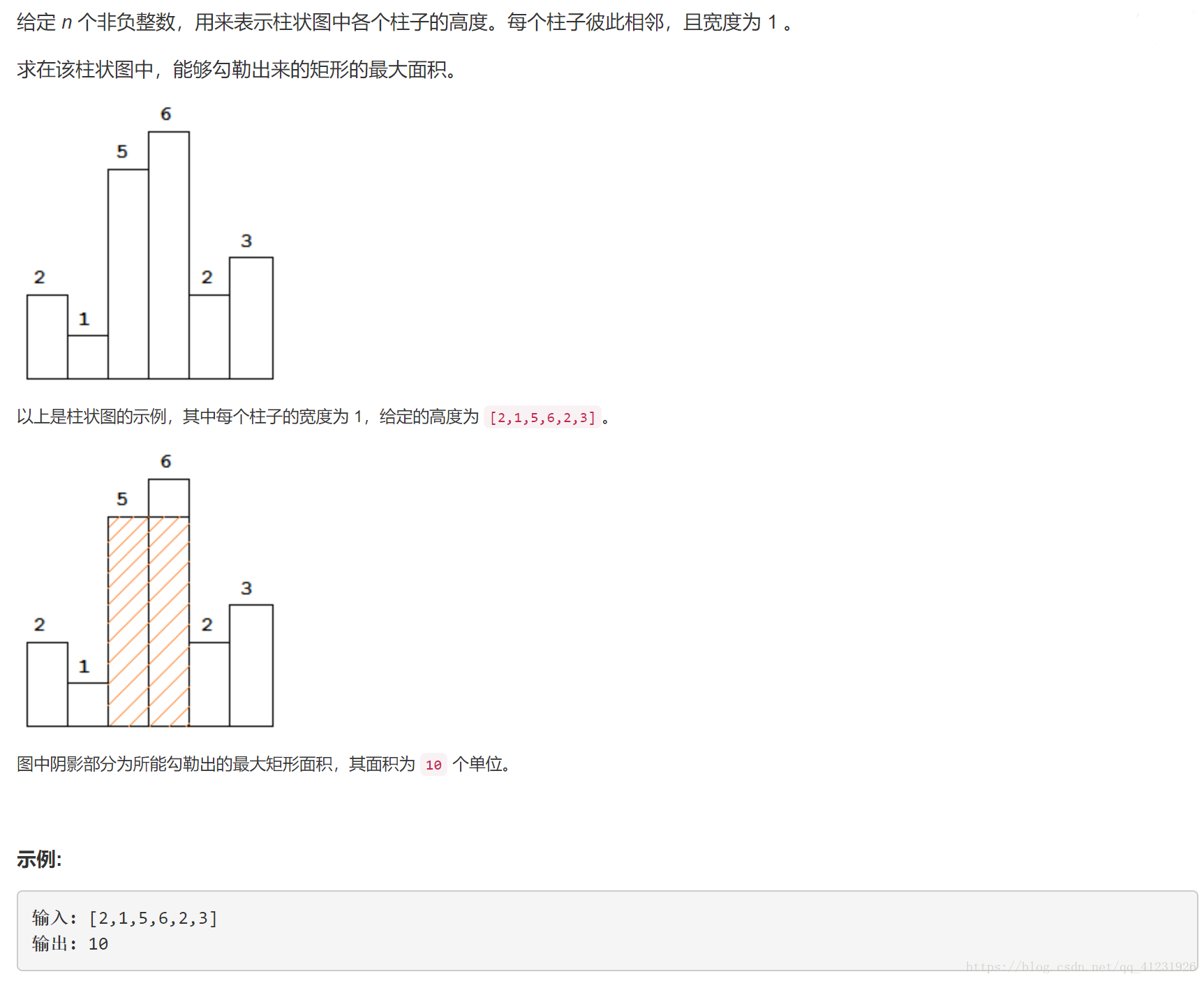
题目描述：

知识点：栈

思路一：对于每一个位置寻求其所在高度的最大矩形

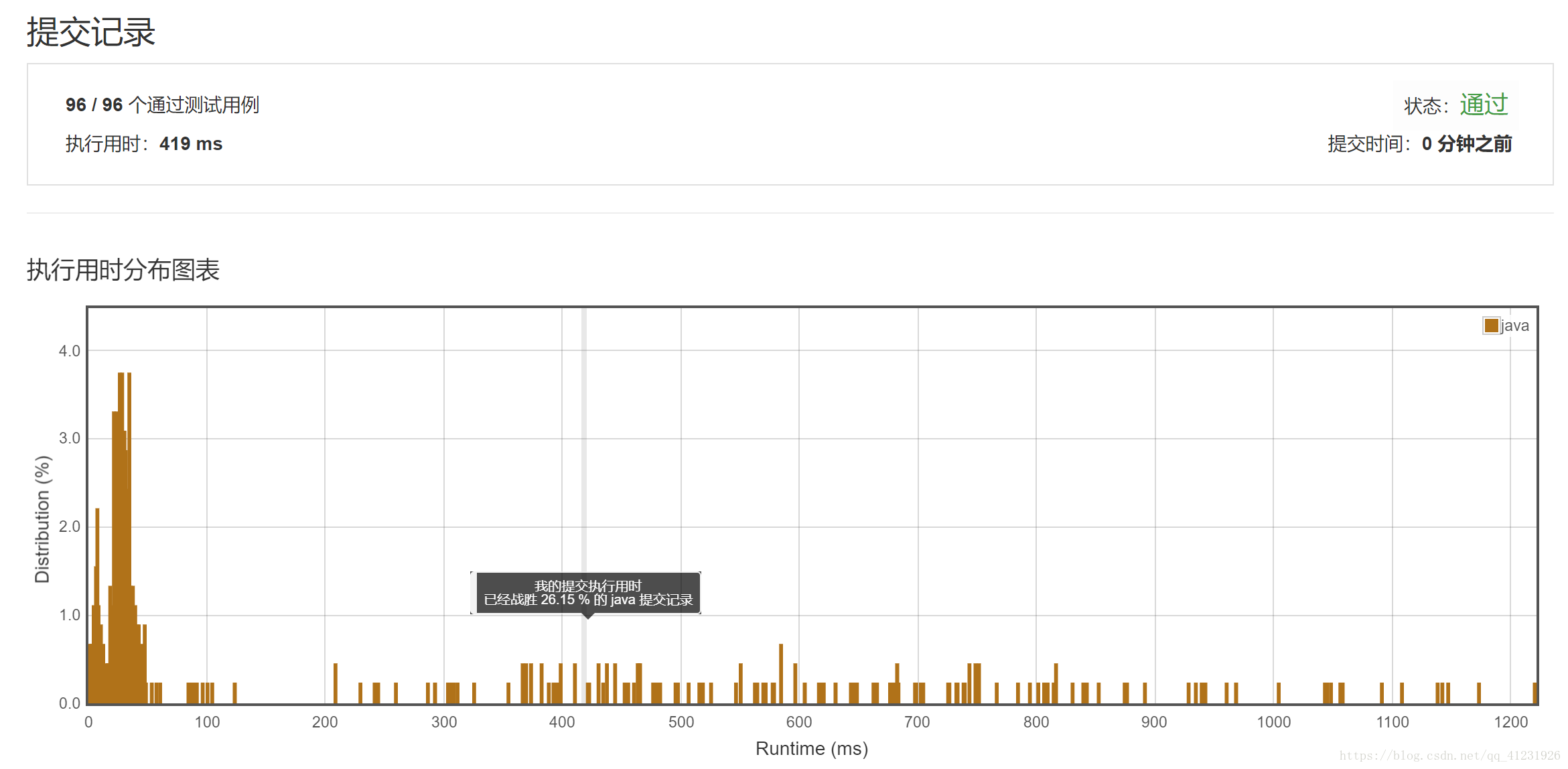
这是我的第一思路。对于数组中的每一个元素，都寻求其对应高度的最大矩形，求n个结果中的最大值即为最大矩形的面积，其中n为heights数组的长度。

时间复杂度根据数组值有所不同，但一定介于O(n)~O(n ^ 2)之间。空间复杂度是O(1)。

JAVA代码：

public class Solution {

    public int largestRectangleArea(int[] heights) {
        int result = 0;
        int n = heights.length;
        for (int i = 0; i < n; i++) {
            int left = i;
            for (; left >= 0; left--) {
                if(heights[left] < heights[i]){
                    break;
                }
            }
            int right = i;
            for (; right < n; right++) {
                if(heights[right] < heights[i]){
                    break;
                }
            }
            result = Math.max(result, heights[i] * (right - left - 1));
        }
        return result;
    }
}

LeetCode解题报告：

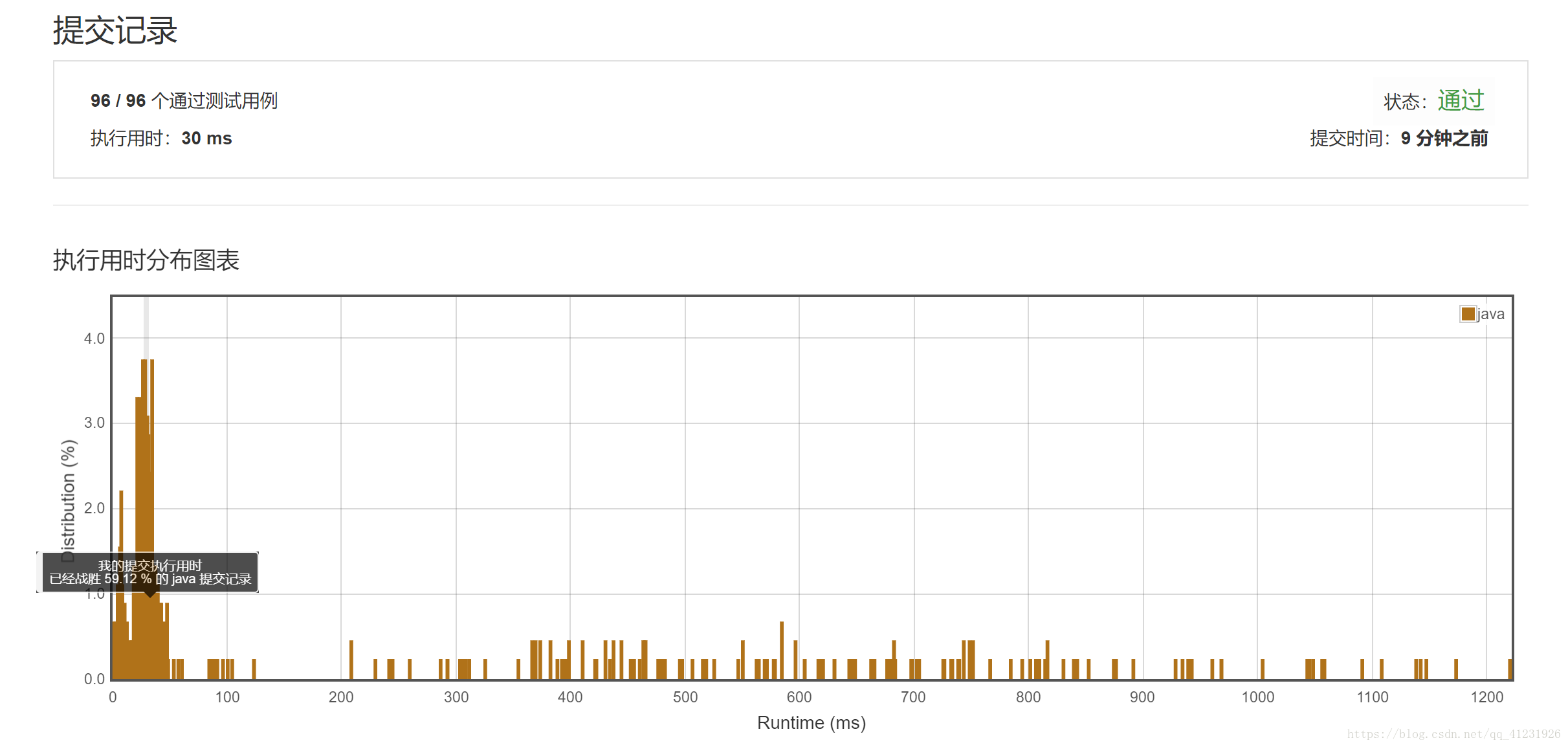
思路二：利用栈先进后出的特性保存之前遍历的每一个索引

如果当前遍历的元素小于栈顶元素，我们就可以进行如下循环：

首先弹出栈顶元素，记录其值为index。

计算矩形左边界。如果此时栈为空，我们记录其左边界为-1。否则，我们将栈顶元素的值作为左边界。

每一次循环过程都可以计算出一个面积值。

循环结束后将当前元素入栈，遍历下一个元素。

为了最后能让栈中的所有元素都出栈，在数组的末尾添加一个新元素，其值为0。这样当遍历到最后一个元素时，确保所有元素都能出栈。

时间复杂度和空间复杂度均是O(n)。

JAVA代码：

public class Solution {

    public int largestRectangleArea(int[] heights) {
        int n = heights.length;
        int[] newHeights = new int[n + 1];
        for (int i = 0; i < n; i++) {
            newHeights[i] = heights[i];
        }
        newHeights[n] = 0;
        int result = 0;
        Stack<Integer> stack = new Stack<>();
        for (int i = 0; i < n + 1; i++) {
            while(!stack.isEmpty() && newHeights[stack.peek()] >= newHeights[i]){
                int index = stack.pop();
                int left = stack.isEmpty() ? -1 : stack.peek();
                result = Math.max(result, newHeights[index] * (i - left - 1));
            }
            stack.push(i);
        }
        return result;
    }
}

LeetCode解题报告：