目录
报告内容仅供学习参考,请独立完成作业和实验喔~
一、报告摘要
1.1 实验要求
(1) 给定二分类数据集,包含了真实标签和多个算法的预测结果,编程实现混淆矩阵评测,根据指标评价算法的分类性能。
(2)给定回归任务数据集,包含真实标签和多个算法的预测结果,编程实现RMSE、MAE、MAPE三种评测,根据指标评价算法的预测性能。
1.2 实验思路
\qquad 使用Python读取数据集信息,根据公式完成计算后,得到结果后分析实验结论。
1.3 实验结论
\qquad
分类方法效果:方法2>方法3>方法1
\qquad
回归方法效果:方法2>方法3>方法1
二、实验内容
2.1 方法介绍
(1)混淆矩阵评测
\qquad
混淆矩阵也称误差矩阵,是表示精度评价的一种标准格式,也是除了ROC曲线和AUC之外的另一个判断分类好坏程度的方法,用n行n列的矩阵形式来表示。
\qquad
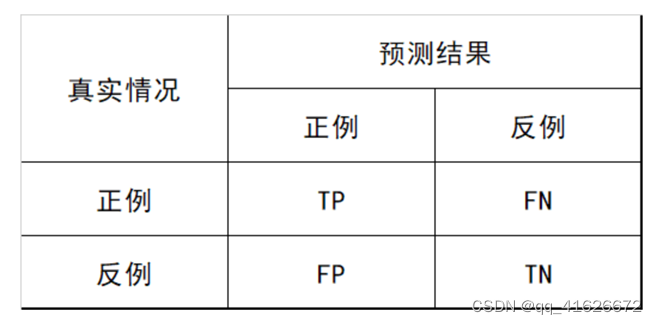
以二分类为例,混淆矩阵由2行2列组成,其组成及各数据意义如下:
TP(True Positive): 真实为0,预测也为0
FN(False Negative): 真实为0,预测为1
FP(False Positive): 真实为1,预测为0
TN(True Negative): 真实为1,预测也为1
\qquad
根据混淆矩阵,可以计算精确度和召回率两个分类评测指标,意义及计算方法如下:
\qquad
精确度 Precision,预测正例中预测正确的占比,计算公式如下
P
=
T
P
T
P
+
F
P
P = \frac{TP}{TP+FP}
P=TP+FPTP
\qquad
召回率 Recall,真实正例中预测正确的占比,计算公式如下
R
=
T
P
T
P
+
F
N
R=\frac{TP}{TP+FN}
R=TP+FNTP
\qquad
精确率和召回率互相影响,理想状态下肯定追求两个都高,但是实际情况是两者相互“制约”:追求精确率高,则召回率就低;追求召回率高,则通常会影响精确率。故我们需要引入例如F-score或P-R曲线图来进行进一步评价。
F
S
c
o
r
e
=
(
1
+
β
2
)
P
r
e
c
i
s
i
o
n
⋅
R
e
c
a
l
l
β
2
⋅
P
r
e
c
i
s
i
o
n
+
R
e
c
a
l
l
F_Score=(1+β^2 ) \frac{Precision⋅Recall}{β^2⋅Precision+Recall}
FScore=(1+β2)β2⋅Precision+RecallPrecision⋅Recall
\qquad
其中,β如果取1,表示Precision与Recall一样重要;β如果取小于1,表示Precision比Recall重要;β如果取大于1,表示Recall比Precision重要
(2)RMSE均方根误差
\qquad
又叫标准误差,用于回归评测,指示模型在预测中会产生多大的误差。RMSE的值越小,说明数据精确度越高。其计算公式如下:
R
M
S
E
=
1
m
∑
i
=
1
m
(
y
i
−
y
i
^
)
2
RMSE=\sqrt{\frac{1}{m}\sum^m_{i=1}(y_i-\hat{y_i})^2}
RMSE=m1i=1∑m(yi−yi^)2
(3)MAE平均绝对误差
\qquad
用于回归评测,平均绝对误差可以准确反映实际预测误差的大小。MAE的值越小,说明数据精确度越高。其计算公式如下:
M
A
E
=
1
m
∑
i
=
1
m
∣
(
y
i
−
y
i
^
)
∣
MAE=\frac{1}{m}\sum^m_{i=1}|(y_i-\hat{y_i})|
MAE=m1i=1∑m∣(yi−yi^)∣
(4)MAPE平均绝对百分比误差
\qquad
用于回归评测,平均绝对百分比误差是平均绝对误差的变形,采用百分比的形式,更容易理解。MAPE的值越小,说明数据精确度越高。其计算公式如下:
M
A
P
E
=
1
m
∑
i
=
1
m
∣
(
y
i
−
y
i
^
)
y
i
∣
MAPE=\frac{1}{m}\sum^m_{i=1}|\frac{(y_i-\hat{y_i})}{y_i}|
MAPE=m1i=1∑m∣yi(yi−yi^)∣
2.2 实验细节
2.2.1 实验环境
硬件环境:Intel® Core™ i5-10300H CPU + 16G RAM
软件环境:Windows 11 家庭中文版 + Python 3.8
2.2.2 部分核心代码
(1)分类评测指标
for i in range(0,len(target)): #混淆矩阵统计
if target[i] == "1" and pred[i]=="1":
tp = tp+1
elif target[i] == "1" and pred[i]=="0":
fn = fn+1
elif target[i] == "0" and pred[i]=="1":
fp = fp+1
elif target[i] == "0" and pred[i]=="0":
tn = tn+1
p_1 = tp/(tp+fp) #计算精确度
r_1 = tp/(tp+fn) #计算召回率
(2)回归评测指标
for i in range(0,n): #求Σ过程
pow_sum = pow_sum + math.pow(target[i]-pred[i],2) #RMSE差平方
mae = mae + abs(target[i]-pred[i]) #MAE差的绝对值
if target[i] == 0: #MAPE需要分情况处理
if pred != 0:
mape = mape+1
else:
mape = mape + abs((target[i]-pred[i])/target[i])
rmse = math.sqrt(pow_sum/n) #RMSE求均值后开方
mae = mae/n #MAE求均值
mape = mape/n*100 #MAPE求均值后转换为百分比
2.2.3 实验与理论内容的不同点
\qquad
本次实验与理论内容的不同点主要集中于MAPE的计算上,根据如下公式
M
A
P
E
=
1
m
∑
i
=
1
m
∣
(
y
i
−
y
i
^
)
y
i
∣
MAPE=\frac{1}{m}\sum^m_{i=1}|\frac{(y_i-\hat{y_i})}{y_i}|
MAPE=m1i=1∑m∣yi(yi−yi^)∣
\qquad
即在计算Σ时,每一项都需要除以真实值,但此时的真实值可能为0,就出现了除以0的情况,无法计算。对于这种情况,我选择的方法是,对于真实值为0的数据,人工设置其在这一点求和的值为0或1,经过改变后的公式如下:
M
A
P
E
=
1
m
∑
i
=
1
m
∣
a
i
y
i
∣
MAPE =\frac{1}{m}\sum_{i=1}^{m}{|\frac{a_i}{y_i}|}
MAPE=m1i=1∑m∣yiai∣
{
0
,
y
i
=
0
a
n
d
y
i
^
=
0
1
,
y
i
=
0
a
n
d
y
i
^
≠
0
y
i
−
y
i
^
,
y
i
≠
0
a
n
d
y
i
^
≠
0
\begin{cases}0,y_i=0\ and\ \widehat{{\ y}_i}=0\\1,y_i=0\ and\ \widehat{{\ y}_i}\neq0\\y_i-\widehat{y_i},y_i\neq0\ and\ \widehat{{\ y}_i}\neq0\end{cases}
⎩
⎨
⎧0,yi=0 and yi
=01,yi=0 and yi
=0yi−yi
,yi=0 and yi
=0
\qquad
原因如下:当预测值为0时且实际值为0时,此时在该点的误差为0,与真实值无关,故此处的误差加0;当预测值为0且真实值不为0时,此时将0看作无穷小,当任意一个非零实数除以无穷小量得到的一定为一个无穷大量,而我们这里由于计算的是百分比,因此最大即为1,故此处误差加1;当预测值和真实值均不为0时,可按照理论公式正常计算。
2.3 实验数据介绍
\qquad
实验数据分为二分类数据集BinaryClassification_dataset.csv和回归预测数据集Regression_dataset.csv。
\qquad
二分类数据集共33条数据,每条数据包括真实值和三种分类方式的分类值。
| Target | Pred_1 | Pred_2 | Pred_3 |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 |
\qquad 回归预测数据集共20条数据,每条数据包括真实值和三种回归方式的预测值。
| Target | Pred_1 | Pred_2 | Pred_3 |
|---|---|---|---|
| 4.5 | 3 | 4.8 | 5.9 |
| 5 | 4 | 4.2 | 4 |
| 6 | 7.2 | 5.4 | 8 |
| 5.5 | 5.1 | 5.1 | 6.7 |
2.4 评价指标介绍
\qquad
对于分类数据,评价指标选用精确度Precession和召回率Recall,意义及计算方法见2.1方法介绍。
\qquad
对于回归数据,评价指标选用RMSE均方根误差、MAE平均绝对误差、MAPE平均绝对百分比误差,意义及计算方法见2.1方法介绍。
2.5 实验结果分析
\qquad
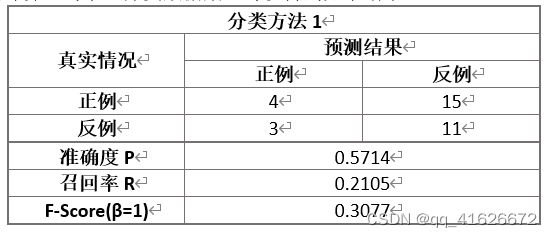
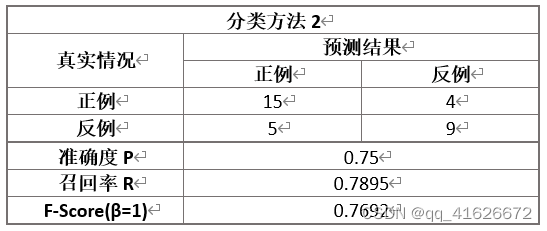
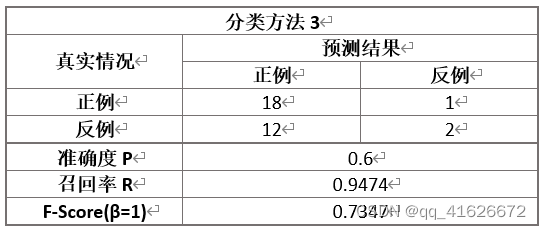
根据计算,对于二分类数据集,可以得到如下结果:
\qquad
根据上述计算我们可以看出,当准确度和召回率相同重要时,分类方法2的整体效果最好,其次是分类方法3,效果最差的是分类方法1.
\qquad
对于回归数据集,可以得到如下结果:
| 回归方法 | RMSE | MAE | MAPE |
|---|---|---|---|
| 方法1 | 3.3817 | 2.53 | 34.0756 |
| 方法2 | 0.7855 | 0.69 | 14.1568 |
| 方法3 | 1.6445 | 1.485 | 25.6939 |
\qquad 根据上述计算结果我们可以看出方法2的三项指标均为最低,回归预测效果最好,其次是方法3,效果最差的是方法1.
三、总结及问题说明
\qquad
本次实验的主要内容为分类与回归性能的评测,通过计算分类算法的混淆矩阵、精确度Precision和召回率Recall,以及回归算法的RMSE均方根误差、MAE平均绝对误差和MAPE平均绝对百分比误差,对数据集的3种方法得到的结果进行评测,得到三种算法的性能好坏。
\qquad
在本次实验中,主要遇到的问题为计算MAPE时除零的问题,实际与理论存在差别,需要根据资料和实际情况进行具体的修改和解决。
四、参考文献
[1] 周志华. 机器学习[M]. 清华大学出版社, 2016.
[2] 均方根值(RMS) 均方根误差(RMSE) 标准差(Standard Deviation)[EB/OL]. [2022-4-27].https://blog.csdn.net/u011594486/article/details/43666871.
附录:实验代码
'''
二分类
'''
import csv
file = '.\BinaryClassification_dataset.csv'
with open(file) as f:
data_list = [i for i in csv.reader(f)] # csv.reader 读取到的数据是list类型
print(data_list)
target = []
pred_1 = []
pred_2 = []
pred_3 = []
for i in data_list:
target.append(i[0])
pred_1.append(i[1])
pred_2.append(i[2])
pred_3.append(i[3])
target.pop(0)
pred_1.pop(0)
pred_2.pop(0)
pred_3.pop(0)
tp_1 = 0
fn_1 = 0
fp_1 = 0
tn_1 = 0
p_1 = 0
r_1 = 0
for i in range(0,len(target)):
if target[i] == "1" and pred_1[i]=="1":
tp_1 = tp_1+1
elif target[i] == "1" and pred_1[i]=="0":
fn_1 = fn_1+1
elif target[i] == "0" and pred_1[i]=="1":
fp_1 = fp_1+1
elif target[i] == "0" and pred_1[i]=="0":
tn_1 = tn_1+1
p_1 = tp_1/(tp_1+fp_1)
r_1 = tp_1/(tp_1+fn_1)
print("tp_1: "+str(tp_1))
print("fn_1: "+str(fn_1))
print("fp_1: "+str(fp_1))
print("tn_1: "+str(tn_1))
print("p_1: "+str(p_1))
print("r_1: "+str(r_1))
print("f_score: "+str(2*(p_1*r_1)/(p_1+r_1)))
tp_2 = 0
fn_2 = 0
fp_2 = 0
tn_2 = 0
p_2 = 0
r_2 = 0
for i in range(0,len(target)):
if target[i] == "1" and pred_2[i]=="1":
tp_2 = tp_2+1
elif target[i] == "1" and pred_2[i]=="0":
fn_2 = fn_2+1
elif target[i] == "0" and pred_2[i]=="1":
fp_2 = fp_2+1
elif target[i] == "0" and pred_2[i]=="0":
tn_2 = tn_2+1
p_2 = tp_2/(tp_2+fp_2)
r_2 = tp_2/(tp_2+fn_2)
print("tp_2: "+str(tp_2))
print("fn_2: "+str(fn_2))
print("fp_2: "+str(fp_2))
print("tn_2: "+str(tn_2))
print("p_2: "+str(p_2))
print("r_2: "+str(r_2))
print("f_score: "+str(2*(p_2*r_2)/(p_2+r_2)))
tp_3 = 0
fn_3 = 0
fp_3 = 0
tn_3 = 0
p_3 = 0
r_3 = 0
for i in range(0,len(target)):
if target[i] == "1" and pred_3[i]=="1":
tp_3 = tp_3+1
elif target[i] == "1" and pred_3[i]=="0":
fn_3 = fn_3+1
elif target[i] == "0" and pred_3[i]=="1":
fp_3 = fp_3+1
elif target[i] == "0" and pred_3[i]=="0":
tn_3 = tn_3+1
p_3 = tp_3/(tp_3+fp_3)
r_3 = tp_3/(tp_3+fn_3)
print("tp_3: "+str(tp_3))
print("fn_3: "+str(fn_3))
print("fp_3: "+str(fp_3))
print("tn_3: "+str(tn_3))
print("p_3: "+str(p_3))
print("r_3: "+str(r_3))
print("f_score: "+str(2*(p_3*r_3)/(p_3+r_3)))
'''
回归
'''
import csv
import math
file = '.\Regression_dataset.csv'
with open(file) as f:
data_list = [i for i in csv.reader(f)] # csv.reader 读取到的数据是list类型
print(data_list)
target = []
pred_1 = []
pred_2 = []
pred_3 = []
for i in data_list:
target.append(i[0])
pred_1.append(i[1])
pred_2.append(i[2])
pred_3.append(i[3])
target.pop(0)
pred_1.pop(0)
pred_2.pop(0)
pred_3.pop(0)
target=list(map(float,target))
pred_1=list(map(float,pred_1))
pred_2=list(map(float,pred_2))
pred_3=list(map(float,pred_3))
pow_sum_1 = 0
rmse_1 = 0
mae_1 = 0
mape_1 = 0
pow_sum_2 = 0
rmse_2 = 0
mae_2 = 0
mape_2 = 0
pow_sum_3 = 0
rmse_3 = 0
mae_3 = 0
mape_3 = 0
n = len(target)
for i in range(0,n):
pow_sum_1 = pow_sum_1 + math.pow(target[i]-pred_1[i],2)
pow_sum_2 = pow_sum_2 + math.pow(target[i]-pred_2[i],2)
pow_sum_3 = pow_sum_3 + math.pow(target[i]-pred_3[i],2)
mae_1 = mae_1 + abs(target[i]-pred_1[i])
mae_2 = mae_2 + abs(target[i]-pred_2[i])
mae_3 = mae_3 + abs(target[i]-pred_3[i])
if target[i] == 0:
if pred_1 != 0:
mape_1 = mape_1+1
if pred_2 != 0:
mape_2 = mape_2+1
if pred_3 != 0:
mape_3 = mape_3+1
else:
mape_1 = mape_1 + abs((target[i]-pred_1[i])/target[i])
mape_2 = mape_2 + abs((target[i]-pred_2[i])/target[i])
mape_3 = mape_3 + abs((target[i]-pred_3[i])/target[i])
rmse_1 = math.sqrt(pow_sum_1/n)
rmse_2 = math.sqrt(pow_sum_2/n)
rmse_3 = math.sqrt(pow_sum_3/n)
mae_1 = mae_1/n
mae_2 = mae_2/n
mae_3 = mae_3/n
mape_1 = mape_1/n*100
mape_2 = mape_2/n*100
mape_3 = mape_3/n*100
print("RMSE")
print(rmse_1)
print(rmse_2)
print(rmse_3)
print("MAE")
print(mae_1)
print(mae_2)
print(mae_3)
print("MAPE")
print(str(mape_1)+"%")
print(str(mape_2)+"%")
print(str(mape_3)+"%")