Day14【二叉树】二叉树的深度优先遍历

先介绍几个不同的二叉树种类

满二叉树：若存在某层，则层均被填满

完全二叉树：其余层均填满，且最底层的节点都集中在该层最左边的若干位置

二叉搜索树：左子树节点值均小于根节点，右子树节点值均大于根节点值

平衡二叉搜索树：左右子树高度差不超过1的二叉搜索树

遍历方式：

深度优先（递归/通过栈迭代）

二叉树的前序遍历

二叉树的后序遍历

二叉树的中序遍历

递归遍历

文章讲解

递归把握一个关键点：确定这个递归调用能干什么事

递归三部曲（每一步都考虑一下那个关键点）

确定递归的参数和返回值
确定终止条件
确定单层递归的逻辑（往往想到能不能利用本身递归函数解决子问题）

以前序遍历来举例思考步骤（所谓前中后序，是指遍历根节点的顺序：根左右、左根右、左右根）

首先思考递归调用能干什么事：这个递归调用能够前序遍历以当前节点为根的树

然后递归三部曲

确定参数与返回值：递归调用能够前序遍历以当前节点为根的树，总要把当前节点传进去，然后传入 vector 来存储遍历结果，不需要什么返回值

void traversal(TreeNode* cur, vector<int>& vec)

确定终止条件：递归调用能够前序遍历以当前节点为根的树，如果当前节点为空了，就能够return了

if (cur == NULL) return;

确定单层递归逻辑：递归调用需要实现前序遍历以当前节点为根的树，同时考虑到能不能利用本身递归函数解决子问题。思考一下假如传入当前节点，要开始写前序遍历的逻辑了。首先，我们很容易遍历当前根节点，主要考虑怎么遍历左子树，遍历右子树。发现利用本身递归函数能够实现左子树右子树的遍历，因为本身递归函数的作用就是”前序遍历以当前节点为根的树“

vec.push_back(cur->val);    // 中
traversal(cur->left, vec);  // 左
traversal(cur->right, vec); // 右

我们看到，在递归三部曲进行的时候，始终要把握这个递归函数是干什么的

下面是完整前序遍历代码

class Solution {
public:
    void traversal(TreeNode* cur, vector<int>& vec) {
        if (cur == NULL) return;
        vec.push_back(cur->val);    // 中
        traversal(cur->left, vec);  // 左
        traversal(cur->right, vec); // 右
    }
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> result;
        traversal(root, result);
        return result;
    }
};

中序、后序略（简单交换一下代码顺序即可）

迭代遍历

文章讲解

深度优先通过栈迭代

前序遍历示意图

入栈根节点
然后只要栈非空，就执行循环：出栈访问某节点，并将该节点的右子树根节点和左子树根节点（若非空）入栈（先入右再入左，因为出栈表示访问，这样出栈遍历访问顺序才能先左后右）

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        vector<int> result;
        if (root == NULL) return result;
        st.push(root);    // 入栈根节点
        while (!st.empty()) {    // 只要栈非空，执行循环
            TreeNode* node = st.top();                       // 出栈遍历这个节点
            st.pop();
            result.push_back(node->val);
            if (node->right) st.push(node->right);           // 该节点右子树根入栈（若非空）
            if (node->left) st.push(node->left);             // 该节点左子树根入栈（若非空）
        }
        return result;
    }
};

后序遍历

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        vector<int> result;
        if (root == NULL) return result;
        st.push(root);
        while (!st.empty()) {
            TreeNode* node = st.top();
            st.pop();
            result.push_back(node->val);
            if (node->left) st.push(node->left); // 相对于前序遍历，这更改一下入栈顺序 （空节点不入栈）
            if (node->right) st.push(node->right); // 空节点不入栈
        }
        reverse(result.begin(), result.end()); // 将结果反转之后就是左右中的顺序了
        return result;
    }
};

中序遍历

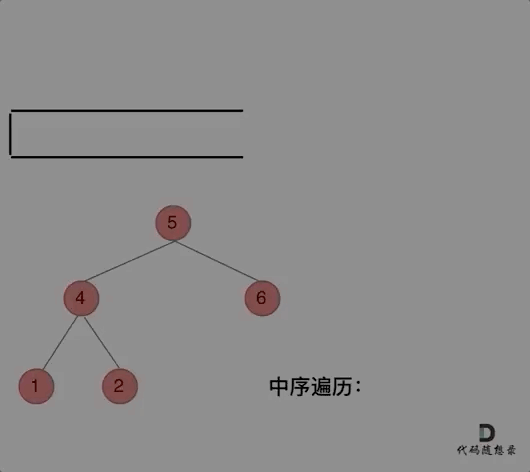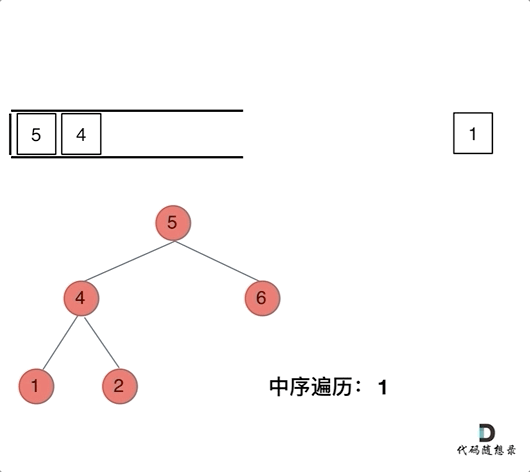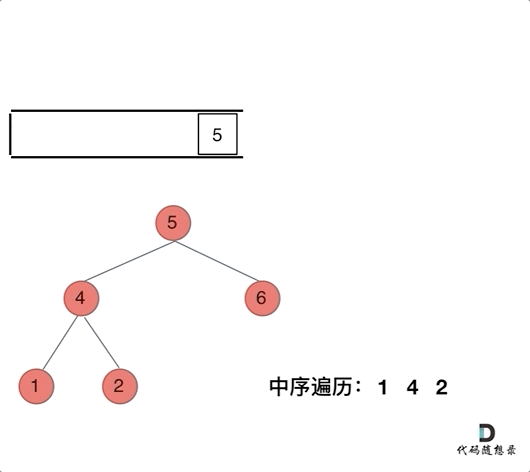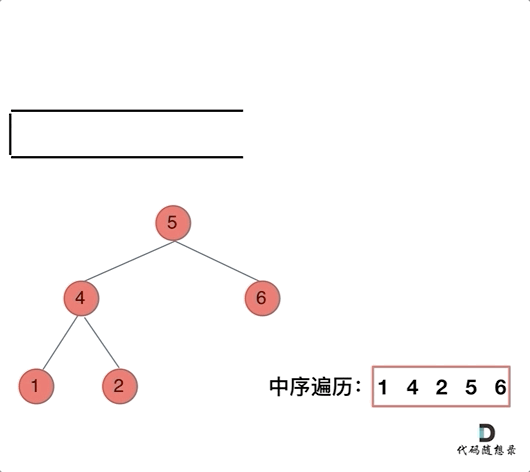
中序遍历不同于前两个遍历方式，前两种都用了出栈访问，并入栈子节点，访问根节点和入栈根节点的子节点操作一气呵成，顺序一致。那么再看看中序遍历，入栈二叉树根节点时，需要一层一层入栈其下层左子树根节点，直到入栈了树左边的最底部，再开始出栈访问节点（也就是把节点的数值放进result数组中），这就造成了入栈该节点的子节点和访问该节点顺序是不一致的。

需要换一种方法，中序遍历的迭代法了解流程即可：每入栈一个节点，则需要要一层一层入栈其下层左子树节点，出栈访问的时候需要判断是否需要入栈其右子树根节点

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
    stack<TreeNode *> st;
public:
    vector<int> inorderTraversal(TreeNode* root) {
        push(root);
        vector<int> res;
        while (!st.empty()) {
            TreeNode * top = st.top();
            st.pop();
            res.push_back(top->val);    //出栈访问
            if (top -> right != nullptr)    //如果需要入栈右子树根节点
                push(top -> right);    //用我们规定的“入栈所有下层左子树根节点”的方式入栈
        }
        return res;
    }
    void push(TreeNode * node) {    //每入栈一个节点，需要一层一层入栈其下层左子树节点
        while (node != nullptr)
        {
            st.push(node);
            node = node -> left;
        }
    }
};

回顾总结

重点掌握递归的思路，递归的关键点和递归三部曲

迭代只需要知道：对于深度优先遍历树，是利用栈这个数据结构实现的