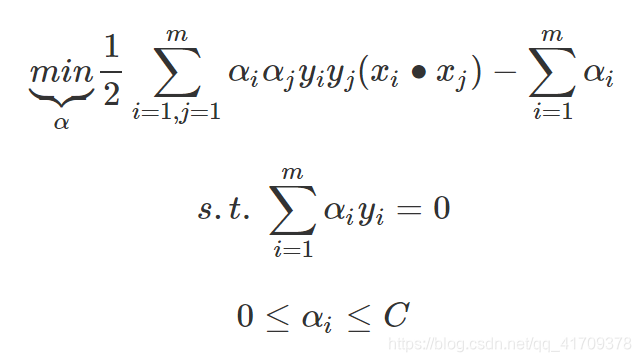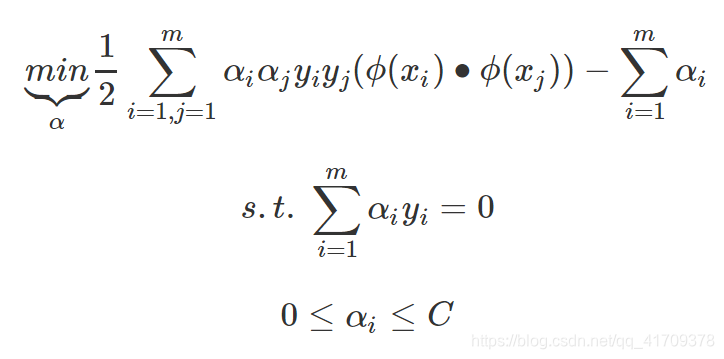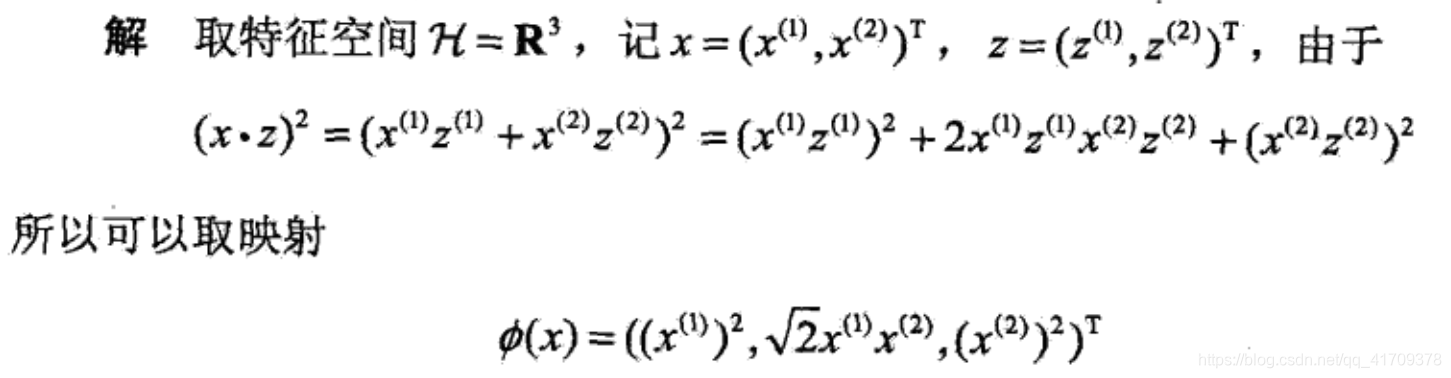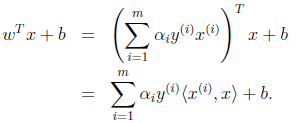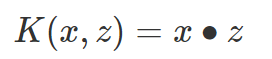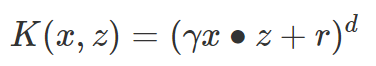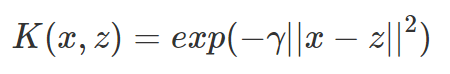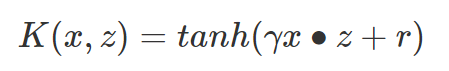我们之前讨论的情况分两种,在样例线性可分的假设上,介绍了SVM的硬间隔,当样例线性不可分时,介绍了SVM软间隔,引入松弛变量,将模型进行调整,以保证在不可分的情况下,也能够尽可能地找出分隔超平面。 上两节介绍的SVM硬间隔和SVM软间隔,它们已经可以很好的解决有异常点的线性问题,但是如果本身是非线性的问题,目前来看SVM还是无法很好的解决的。所以本文介绍SVM的核函数技术,能够顺利的解决非线性的问题。
1.前言
为什么要引入核函数:
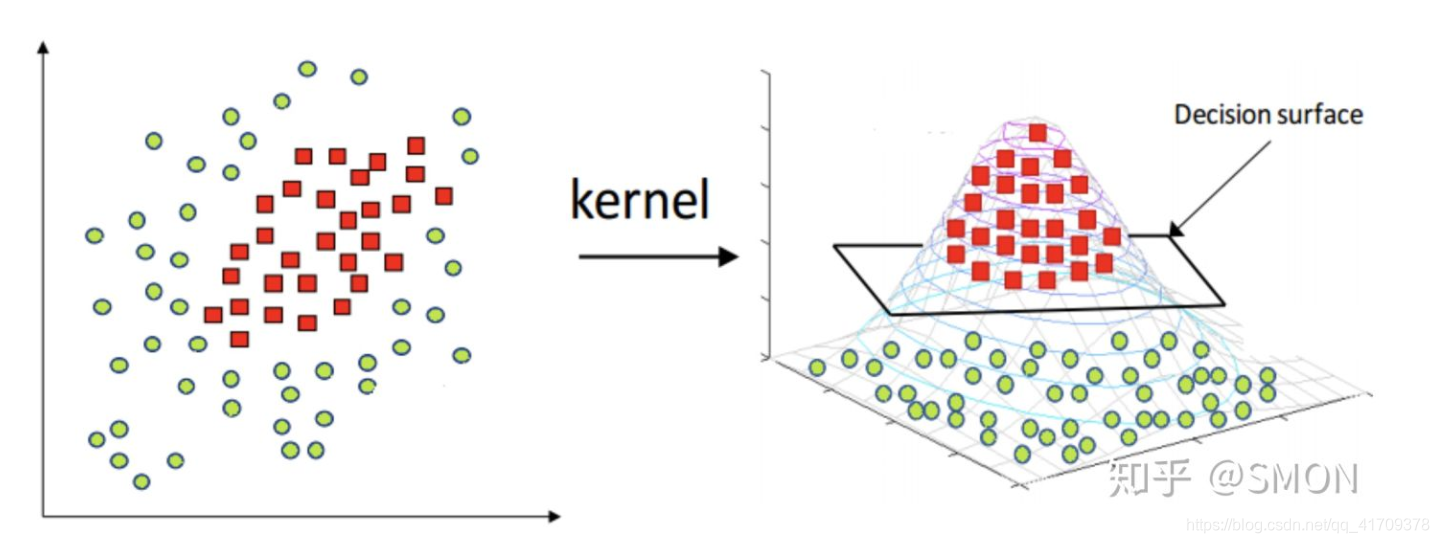
当样本在原始空间线性不可分时,可将样本从原始空间映射到一个更高维的特征空间,使得样本在这个特征空间内线性可分。如下图所示。(图片来自于知乎:SMON)
而引入这样的映射后,所要求解的对偶问题的求解中,无需求解真正的映射函数,而只需要知道其核函数K(x,y)。核函数的定义:K(x,y)=<ϕ(x),ϕ(y)>,即在特征空间的内积等于它们在原始样本空间中通过核函数 K 计算的结果。一方面数据变成了高维空间中线性可分的数据,另一方面不需要求解具体的映射函数,只需要给定具体的核函数即可,这样使得求解的难度大大降低。
2.核函数原理
在解释核函数原理之前,介绍非线性变化。
例如,一个二维的特征数据集 ( x 1 , x 2 ) (x_1, x_2) (x1,x2),这里的 x i x_i xi是实数,结果是y。要找到y与两个特征的变化关系,在线性变化过程中: y = a x 1 + b x 2 y=ax_1+bx_2 y=ax1+bx2找不到合适的参数a,b。于是考虑非线性变化,寻找到合适的参数来反映结果y数据集的特征之间的关系。
在非线性变化中,不再只有两个特征,可能变成了三个特征甚至五个特征,这个过程叫做低维空间到高维空间的映射。
y = a x 1 + b x 2 + c x 1 x 2 y = ax_1+bx_2+cx_1x_2 y=ax1+bx2+cx1x2
y = a x 1 2 + b x 2 2 + c x 1 x 2 + d x 1 + f x 2 y = ax_1^2+bx_2^2+cx_1x_2+dx_1+fx_2 y=ax12+bx22+cx1x2+dx1+fx2
此时,将二维的空间转换成高维的空间,寻找合适的参数来反映原始特征集的变化过程。
核函数的原理和非线性变化的原理如出一辙,也就是说对于在低维线性不可分的数据,在映射到了高维以后,就变成线性可分的了。也就是说,对于SVM线性不可分的低维特征数据,我们可以将其映射到高维,就能线性可分,此时就可以运用前两篇的线性可分SVM的算法思想了。
我们首先回顾下SVM软间隔的模型公式:
注意到上式低维特征仅仅以内积
x
i
∙
x
j
x_i∙x_j
xi∙xj的形式出现,如果我们定义一个低维特征空间到高维特征空间的映射ϕ,将所有特征映射到一个更高的维度,让数据线性可分,我们就可以继续按前两篇的方法来优化目标函数,求出分离超平面和分类决策函数了。也就是说现在的SVM的优化目标函数变成:
公式中的内积从 < x i , x j > <x_i, x_j> <xi,xj>,映射到 < ϕ ( x i ) , ϕ ( x j ) > <\phi \left( {{x_i}} \right), \phi \left( {{x_j}} \right)> <ϕ(xi),ϕ(xj)>中时,在高维计算向量的内积是很困难的。比如最初的特征是n维的,我们将其映射到 n 2 n^2 n2维,然后再计算,这样需要 O ( n 2 ) O(n^2) O(n2)的时间。那么我们能不能想办法减少计算时间呢?
引入核函数形式化定义,如果原始特征内积是 < x , z > <x, z> <x,z>,映射后为 < ϕ ( x ) , ϕ ( z ) > <\phi \left( {{x}} \right), \phi \left( {{z}} \right)> <ϕ(x),ϕ(z)>,那么定义核函数(Kernel)为 K ( x , z ) = ϕ ( x ) T ϕ ( z ) K\left( {x,z} \right) = \phi {\left( x \right)^T}\phi \left( z \right) K(x,z)=ϕ(x)Tϕ(z),映射函数为 ϕ ( x ) \phi \left( {{x}} \right) ϕ(x)。
先看一个例子,假设x和z都是2维的输入空间,核函数是
K
(
x
,
z
)
=
(
x
⋅
z
)
2
K\left( {x,z} \right) =(x·z)^2
K(x,z)=(x⋅z)2,将二维特征空间映射成三维的空间中
H
=
R
3
{\rm H} = {R^3}
H=R3。
得到了
ϕ
(
x
)
=
(
(
x
(
1
)
)
2
,
2
x
(
1
)
x
(
2
)
,
(
x
(
2
)
)
2
)
T
\phi \left( x \right) = {\left( {{{\left( {{x^{\left( 1 \right)}}} \right)}^2},\sqrt 2 {x^{\left( 1 \right)}}{x^{\left( 2 \right)}},{{\left( {{x^{\left( 2 \right)}}} \right)}^2}} \right)^T}
ϕ(x)=((x(1))2,2x(1)x(2),(x(2))2)T,
ϕ
(
z
)
=
(
(
z
(
1
)
)
2
,
2
z
(
1
)
z
(
2
)
,
(
z
(
2
)
)
2
)
T
\phi \left( z\right) = {\left( {{{\left( {{z^{\left( 1 \right)}}} \right)}^2},\sqrt 2 {z^{\left( 1 \right)}}{z^{\left( 2 \right)}},{{\left( {{z^{\left( 2 \right)}}} \right)}^2}} \right)^T}
ϕ(z)=((z(1))2,2z(1)z(2),(z(2))2)T,此时
<
ϕ
(
x
)
,
ϕ
(
z
)
>
<\phi \left( {{x}} \right), \phi \left( {{z}} \right)>
<ϕ(x),ϕ(z)>的值为
(
x
⋅
z
)
2
=
K
(
x
,
z
)
(x·z)^2 = K\left( {x,z} \right)
(x⋅z)2=K(x,z).
这个时候发现我们可以只计算原始特征x和z内积的平方,也就是说我们的时间复杂度为 O ( n ) O(n) O(n),就等价与计算映射后特征的内积 < ϕ ( x i ) , ϕ ( x j ) > <\phi \left( {{x_i}} \right), \phi \left( {{x_j}} \right)> <ϕ(xi),ϕ(xj)>。
当然,在使用了核函数是
K
(
x
,
z
)
=
(
x
⋅
z
)
2
K\left( {x,z} \right) =(x·z)^2
K(x,z)=(x⋅z)2,映射函数可以不同,例如
H
=
R
3
{\rm H} = {R^3}
H=R3,
ϕ
(
x
)
=
(
(
x
(
1
)
)
2
,
2
x
(
1
)
x
(
2
)
,
(
x
(
2
)
)
2
)
T
\phi \left( x \right) = {\left( {{{\left( {{x^{\left( 1 \right)}}} \right)}^2},\sqrt 2 {x^{\left( 1 \right)}}{x^{\left( 2 \right)}},{{\left( {{x^{\left( 2 \right)}}} \right)}^2}} \right)^T}
ϕ(x)=((x(1))2,2x(1)x(2),(x(2))2)T
H
=
R
3
{\rm H} = {R^3}
H=R3,
ϕ
(
x
)
=
1
2
(
(
x
(
1
)
)
2
−
(
x
(
2
)
)
2
,
2
x
(
1
)
x
(
2
)
,
(
x
(
1
)
)
2
−
(
x
(
2
)
)
2
)
T
\phi \left( x \right) = \frac{1}{{\sqrt 2 }}{\left( {{{\left( {{x^{(1)}}} \right)}^2} - {{\left( {{x^{(2)}}} \right)}^2},2{x^{\left( 1 \right)}}{x^{\left( 2 \right)}},{{\left( {{x^{(1)}}} \right)}^2} - {{\left( {{x^{(2)}}} \right)}^2}} \right)^T}
ϕ(x)=21((x(1))2−(x(2))2,2x(1)x(2),(x(1))2−(x(2))2)T
H
=
R
4
{\rm H} = {R^4}
H=R4,
ϕ
(
x
)
=
(
(
x
(
1
)
)
2
,
x
(
1
)
x
(
2
)
,
x
(
1
)
x
(
2
)
,
(
x
(
2
)
)
2
)
T
\phi \left( x \right) = {\left( {{{\left( {{x^{(1)}}} \right)}^2},{x^{\left( 1 \right)}}{x^{\left( 2 \right)}},{x^{\left( 1 \right)}}{x^{\left( 2 \right)}},{{\left( {{x^{(2)}}} \right)}^2}} \right)^T}
ϕ(x)=((x(1))2,x(1)x(2),x(1)x(2),(x(2))2)T
但是映射函数的内积仍然满足
<
ϕ
(
x
)
,
ϕ
(
z
)
>
=
(
x
⋅
z
)
2
=
K
(
x
,
z
)
<\phi \left( {{x}} \right), \phi \left( {{z}} \right)>=(x·z)^2 = K\left( {x,z} \right)
<ϕ(x),ϕ(z)>=(x⋅z)2=K(x,z)。所以,得出一个结论在使用了核函数之后,不用找映射函数到底是哪一个,如何变化的,找
ϕ
(
x
)
\phi \left( {{x}} \right)
ϕ(x)很麻烦,回想我们之前说过的
只需将 < x ( i ) , x > <x^{(i)},x> <x(i),x>替换成 K ( x ( i ) , x ) K(x^{(i)},x) K(x(i),x),然后值的判断同上。
3.核函数的介绍
由上面的介绍可知,我们只需要定义核函数就可以了。但是如何通过映射 ϕ ( x ) \phi \left( {{x}} \right) ϕ(x)判断给定的一个函数 K ( x , z ) K\left( {x,z} \right) K(x,z)是不是核函数呢?或者说, K ( x , z ) K\left( {x,z} \right) K(x,z)需要满足什么条件才是一个核函数。
通常所说的核函数就是正定核函数,具体证明略显复杂,有兴趣的可以参考《统计学习方法》,或者查看这篇博客:核函数有效性判定.
虽然有了上述定义,但是实际应用时验证
K
(
x
,
z
)
K\left( {x,z} \right)
K(x,z)是否是正定核依然不容易,因此在实际问题中一般使用已有的核函数,下面给出一些常用的核函数。
线性核函数:
线性核函数(Linear Kernel)其实就是我们前两篇的线性可分SVM,也就是说,线性可分SVM我们可以和线性不可分SVM归为一类,区别仅仅在于线性可分SVM用的是线性核函数。
多项式核函数:
多项式核函数(Polynomial Kernel)是线性不可分SVM常用的核函数之一,公式如下:
高斯核函数:
高斯核函数(Gaussian Kernel),在SVM中也称为径向基核函数(Radial Basis Function,RBF),它是非线性分类SVM最主流的核函数。libsvm默认的核函数就是它。公式如下:
Sigmoid核函数:
Sigmoid核函数(Sigmoid Kernel)也是线性不可分SVM常用的核函数之一,公式如下:
4.核函数的选择
1、根据样本量m和特征量n进行选择:
(1)特征相比样本较大(如m=10~1000,n=10000):选逻辑回归或者线性函数SVM
(2)特征较少,样本量中(如m=10~10000,n=1~1000):选择高斯SVM
(3)特征量少,样本多(如m=50000+,n=1~1000):选多项式或高斯SVM
2、核函数优缺点的对比:
参考资料:
1 chrome-extension://ibllepbpahcoppkjjllbabhnigcbffpi/http://cs229.stanford.edu/notes2019fall/cs229-notes3.pdf
2 https://www.cnblogs.com/jerrylead/archive/2011/03/18/1988406.html
3 https://www.cnblogs.com/huangyc/p/9940487.html
4 https://blog.csdn.net/weixin_42398658/article/details/83181762?utm_medium=distribute.pc_relevant_t0.none-task-blog-OPENSEARCH-1.nonecase&depth_1-utm_source=distribute.pc_relevant_t0.none-task-blog-OPENSEARCH-1.nonecase
5 https://blog.csdn.net/batuwuhanpei/article/details/52354822