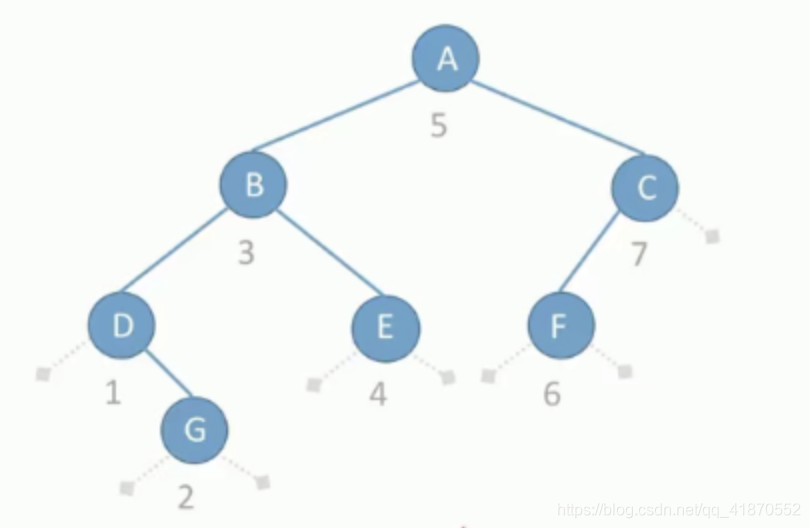
C语言实现二叉树的线索化以及如何遍历线索二叉树！

线索二叉树的结构及数据类型定义

//定义数据类型
typedef char ElemType;

//枚举，Link为0表示不是线索，Thread为1表示为线索
typedef enum {
    Link,
    Thread
} PointerTag;
//结点结构构造
typedef struct BiThrNode {
    ElemType data;//数据域
    struct BiThrNode *lchild, *rchild;//左右孩子指针域
    PointerTag Ltag, Rtag;//标志域，枚举类型
} BiThrNode, *BiThrTree;

BiThrTree pre = NULL;

根据输入结点初始化二叉树

//根据输入结点初始化并建立二叉树
bool CreateBiThrTree(BiThrTree &T) {
    //输入二叉树中的结点的值(一个字符)，空格字符表示空树并构造二叉链表表示的树T
    ElemType ch;
    scanf("%c", &ch);
    getchar();
    if (ch == ' ') {
        T = NULL;
    } else {
        if (!(T = (BiThrTree) malloc(sizeof(BiThrNode)))) {
            return false;
        }
        T->data = ch;                    //生成根结点
        printf("请输入%c的左子树：", ch);
        CreateBiThrTree(T->lchild);        //构造左子树
        printf("请输入%c的右子树：", ch);
        CreateBiThrTree(T->rchild);        //构造右子树
    }
    return true;
}

中序遍历二叉树并线索化

//中序遍历并线索化
void InOrderThreading(BiThrTree T) {
    //如果当前结点没有左孩子，左标志位设为1，左指针域指向上一结点 pre
    if (!T->lchild) {
        T->Ltag = Thread;
        T->lchild = pre;
    }
    //如果 pre 没有右孩子，右标志位设为 1，右指针域指向当前结点。
    if (pre && !pre->rchild) {
        pre->Rtag = Thread;
        pre->rchild = T;
    }
    //pre指向当前结点
    pre = T;
}

//中序遍历二叉树并进行线索化
void InOrder(BiThrTree T) {
    //如果当前结点存在
    if (T) {
        InOrder(T->lchild);//递归当前结点的左子树，进行线索化
        Visit(T);
        InOrderThreading(T);
        InOrder(T->rchild);//递归右子树进行线索化
    }
}

遍历中序线索二叉树

//中序遍历线索二叉树
void InOrderThraverse_Thr(BiThrTree T) {
    while (T) {
        //一直找他的左孩子，查看Ltag是否为Thread（线索），即找到的最后一个为中序序列中排第一的
        while (T->Ltag == Link) {
            T = T->lchild;
        }
        Visit(T);  //操作结点数据
        //当结点右标志位为1时，直接找到其后继结点
        while (T->Rtag == Thread && T->rchild != NULL) {
            T = T->rchild;
            Visit(T);
        }
        //否则，按照中序遍历的规律，找其右子树中最左下的结点，也就是继续循环遍历
        T = T->rchild;
    }
}

项目完整代码

//中序遍历线索二叉树的实现
#include <stdio.h>
#include <stdlib.h>

//定义数据类型
typedef char ElemType;

//枚举，Link为0表示不是线索，Thread为1表示为线索
typedef enum {
    Link,
    Thread
} PointerTag;
//结点结构构造
typedef struct BiThrNode {
    ElemType data;//数据域
    struct BiThrNode *lchild, *rchild;//左右孩子指针域
    PointerTag Ltag, Rtag;//标志域，枚举类型
} BiThrNode, *BiThrTree;

BiThrTree pre = NULL;

//根据输入结点初始化并建立二叉树
bool CreateBiThrTree(BiThrTree &T) {
    //输入二叉树中的结点的值(一个字符)，空格字符表示空树并构造二叉链表表示的树T
    ElemType ch;
    scanf("%c", &ch);
    getchar();
    if (ch == ' ') {
        T = NULL;
    } else {
        if (!(T = (BiThrTree) malloc(sizeof(BiThrNode)))) {
            return false;
        }
        T->data = ch;                    //生成根结点
        printf("请输入%c的左子树：", ch);
        CreateBiThrTree(T->lchild);        //构造左子树
        printf("请输入%c的右子树：", ch);
        CreateBiThrTree(T->rchild);        //构造右子树
    }
    return true;
}

//访问输出的Visit函数
void Visit(BiThrTree T) {    //输出元素的值
    printf("%c ", T->data);
}

//中序遍历线索化
void InOrderThreading(BiThrTree T) {
    //如果当前结点没有左孩子，左标志位设为1，左指针域指向上一结点 pre
    if (!T->lchild) {
        T->Ltag = Thread;
        T->lchild = pre;
    }
    //如果 pre 没有右孩子，右标志位设为 1，右指针域指向当前结点。
    if (pre && !pre->rchild) {
        pre->Rtag = Thread;
        pre->rchild = T;
    }
    //pre指向当前结点
    pre = T;
}

//中序遍历二叉树并进行线索化
void InOrder(BiThrTree T) {
    //如果当前结点存在
    if (T) {
        InOrder(T->lchild);//递归当前结点的左子树，进行线索化
        Visit(T);
        InOrderThreading(T);
        InOrder(T->rchild);//递归右子树进行线索化
    }
}

//中序遍历线索二叉树
void InOrderThraverse_Thr(BiThrTree T) {
    while (T) {
        //一直找他的左孩子，查看Ltag是否为Thread（线索），即找到的最后一个为中序序列中排第一的
        while (T->Ltag == Link) {
            T = T->lchild;
        }
        Visit(T);  //操作结点数据
        //当结点右标志位为1时，直接找到其后继结点
        while (T->Rtag == Thread && T->rchild != NULL) {
            T = T->rchild;
            Visit(T);
        }
        //否则，按照中序遍历的规律，找其右子树中最左下的结点，也就是继续循环遍历
        T = T->rchild;
    }
}

int main() {
    BiThrTree T;
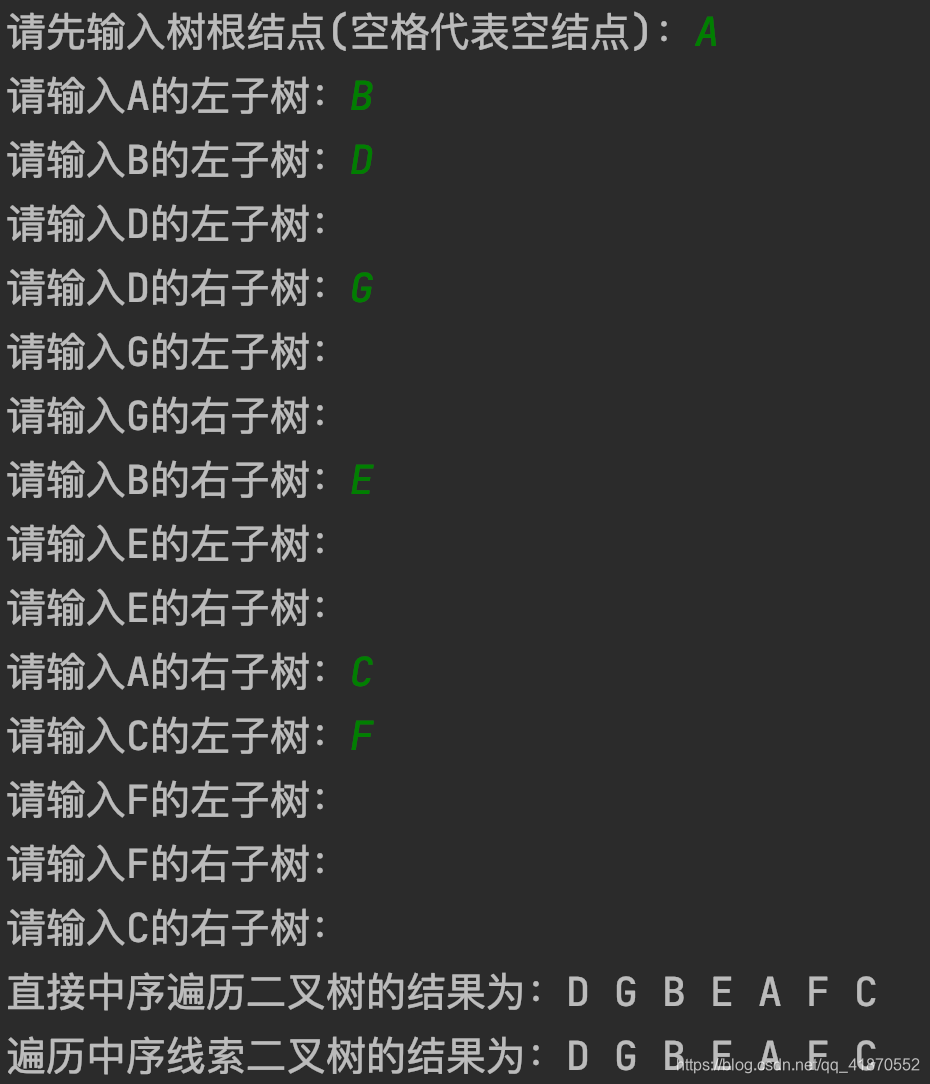
    printf("请先输入树根结点(空格代表空结点)：");
    CreateBiThrTree(T);
    printf("直接中序遍历二叉树的结果为：");
    InOrder(T);
    printf("\n");
    printf("遍历中序线索二叉树的结果为：");
    InOrderThraverse_Thr(T);
    printf("\n");
    return 0;
}

项目完整代码（改进版）

//中序遍历线索二叉树的实现（改进）
#include <stdio.h>
#include <stdlib.h>

//定义数据类型
typedef char ElemType;

//枚举，Link为0表示不是线索，Thread为1表示为线索
typedef enum {
    Link,
    Thread
} PointerTag;
//结点结构构造
typedef struct BiThrNode {
    ElemType data;//数据域
    struct BiThrNode *lchild, *rchild;//左右孩子指针域
    PointerTag Ltag, Rtag;//标志域，枚举类型
} BiThrNode, *BiThrTree;

BiThrTree pre = NULL;

//根据输入结点初始化并建立二叉树
bool CreateBiThrTree(BiThrTree &T) {
    //输入二叉树中的结点的值(一个字符)，空格字符表示空树并构造二叉链表表示的树T
    ElemType ch;
    scanf("%c", &ch);
    getchar();
    if (ch == ' ') {
        T = NULL;
    } else {
        if (!(T = (BiThrTree) malloc(sizeof(BiThrNode)))) {
            return false;
        }
        T->data = ch;                    //生成根结点
        printf("请输入%c的左子树：", ch);
        CreateBiThrTree(T->lchild);        //构造左子树
        printf("请输入%c的右子树：", ch);
        CreateBiThrTree(T->rchild);        //构造右子树
    }
    return true;
}

//访问输出的Visit函数
void Visit(BiThrTree T) {    //输出元素的值
    printf("%c ", T->data);
}

//线索化函数
void OrderThreading(BiThrTree &T) {
    //如果当前结点没有左孩子，左标志位设为1，左指针域指向上一结点 pre
    if (!T->lchild) {
        T->Ltag = Thread;
        T->lchild = pre;
    }
    //如果 pre 没有右孩子，右标志位设为 1，右指针域指向当前结点。
    if (pre && !pre->rchild) {
        pre->Rtag = Thread;
        pre->rchild = T;
    }
    //pre指向当前结点
    pre = T;
}

//中序遍历二叉树
void InOrder(BiThrTree T) {
    //如果当前结点存在（左根右）
    if (T) {
        InOrder(T->lchild);     //递归当前结点的左子树
        Visit(T);
        OrderThreading(T);   //进行线索化
        InOrder(T->rchild);     //递归右子树进行线索化
    }
}

//中序遍历线索二叉树
void InOrderThraverse_Thr(BiThrTree T) {
    while (T) {
        //一直找他的左孩子，查看Ltag是否为Thread（线索），即找到的最后一个为中序序列中排第一的
        while (T->Ltag == Link) {
            T = T->lchild;
        }
        Visit(T);  //操作结点数据
        //当结点右标志位为1时，直接找到其后继结点
        while (T->Rtag == Thread && T->rchild != NULL) {
            T = T->rchild;
            Visit(T);
        }
        //否则，按照中序遍历的规律，找其右子树中最左下的结点，也就是继续循环遍历
        T = T->rchild;
    }
}

//中序遍历——找到以P为根结点的子树中，最后一个被中序遍历的
BiThrNode *InLastNode(BiThrNode *p) {
    //循环找到最右下的结点（不一定为叶子结点）
    while (p->Rtag == Link)
        p = p->rchild;
    return p;
}

//在中序线索二叉树中找到结点P的前驱结点
BiThrNode *InPreNode(BiThrNode *p) {
    //循环找到最右下的结点（不一定为叶子结点）
    if (p->Ltag == Link)
        return InLastNode(p->lchild);
    else
        return p->lchild;
}

//对中序线索二叉树进行逆向中序遍历
void ReInOderThraverse_Thr(BiThrNode *T) {
    for (BiThrNode *p = InLastNode(T); p != NULL; p = InPreNode(p)) {
        Visit(p);
    }
}

//线索二叉树T
void CreatThread(BiThrTree T) {
    if (T) {
        InOrder(T);
        if (!pre->rchild)
            pre->Rtag = Thread;
    }
}

int main() {
    BiThrTree T;
    printf("请先输入树根结点(空格代表空结点)：");
    CreateBiThrTree(T);
    printf("\n");
    printf("直接中序遍历二叉树的结果为：");
    CreatThread(T);
    printf("\n\n");
    printf("正向遍历中序线索二叉树请输入  1\n");
    printf("逆向遍历中序线索二叉树请输入  2\n");
    printf("请选择是采用正向还是逆向输出：");
    int id;
    scanf("%d", &id);
    if (id == 1) {
        printf("正向遍历中序线索二叉树的结果为：");
        InOrderThraverse_Thr(T);
    }
    if (id == 2) {
        printf("逆向遍历中序线索二叉树的结果为：");
        ReInOderThraverse_Thr(T);
    }
    printf("\n");
    return 0;
}

运行效果图