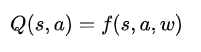提示：转载请注明出处，若本文无意侵犯到您的合法权益，请及时与作者联系。

一、表格式存储与值函数近似

1、维度灾难

在之前的学习中，我们学习的都是传统的强化学习方式，这些方法应用有限，特别是以Q-Learning为代表的表格式算法在处理问题时会存在瓶颈。表格式存储Q值实际上是一种穷举思想，适合于数量较小的离散的数据，但是当我们状态空间十分巨大且连续时，这种表格式存储就变得不合时宜。

这种就是强化学习发展过程中存在的“维度灾难”问题。

2、值函数近似

一种解决这类问题的方法就是价值函数近似（Value Function Approximation），简单来讲就是使用函数映射来代替表格式存储。

通过函数表示，我们就可以处理一个高维度的s，因为最后最后都会通过矩阵运算降维输出为单值的Q。如果我们就用函数w来统一表示函数f的参数，那么就有：

进行值函数近似模拟的关键就是找到这样的函数模拟工具

线性关系可以用常见的线性函数模拟，非线性关系可以使用神经网络来模拟。

使用神经网络来模拟值函数，就是将目前的深度学习技术与强化学习技术结合起来，成为了现在又焕发新生命力的深度强化学习领域。

这一类的代表研究就是Google Deep mind 团队推出的DQN算法，代表应用就是火爆一时的AlphaGo。

二、DQN是什么

 DQN全称叫做Deep Q Network，是Google Deep mind 团队提出的一种融合了神经网络和 Q learning 的强化学习方法。

DQN算法的提出对于强化学习是一个里程碑式的发展，它解决了将神经网络用于传统强化学习的难点：

神经网络基于独立同分布数据的统计方法，而强化学习产生的数据样本是序列相关的，不是独立分布，学习的策略往往不够稳定。

DQN算法则使用了记忆回放机制（Memory Replay）来解决这个问题，这个机制也是深度强化学习领域一个非常重要的技巧。

三、Memory Replay的步骤

记忆回放机制（Memory Replay）是DQN算法中的一个核心机制，具体操作步骤如下：

一、初始化阶段：

初始化一块大小为N的内存空间D

初始化一个有着随机参数的动作-状态模拟函数Q（神经网络eval_net）

初始化一个有着随机参数的动作状态函数（神经网络target_net）

二、在每步的学习阶段：

1、Agent以-greedy选择一个动作a

2、获得Env反馈的立即回报、后继状态

3、将观测值、动作、立即回报、后继观测值组成的transition集合存储到D中，当达到空间最大值之后替换原来的采样样本。

（以下步骤可以以一个固定的频率来进行，不一定需要在每一步中）

4、从D中随机采样一个批量（Batch）的样本

5、计算这些样本的Q现实值：如果下一个步是终止步就直接等于立即回报，否则使用Bellman方程计算

6、使用（现实值-Q估计值）计算一个梯度下降的损失值，并去优化Q的参数。

7、每隔C步学习就将Q参数复制给。

对应的DQN算法如下：

具体的代码示例可以参考我的博客莫烦Python代码实践（四）——DQN基础算法工程化解析

在这篇博客中使用DQN算法来解决走迷宫的案例，使用的是TensorFlow搭建的双层FNN神经网络。