递归:函数的嵌套调用
递归--自己调用自己
递归是一种特殊的循环
递归的过程,实际上是函数的调用,而函数的调用需要栈空间(某一块内存空间)
内存结构:
栈:
1.是一种数据结构,FILO(First Input Last Output)先进后出
2.内存上的一块空间
3.大小有限,
4.存放函数的参数值,局部变量的值等
5.自动申请,自动释放
32位--4G的栈内存空间
2^32-->2^10 * 2^10 * 2^10 *2*2
1024 1024 1024
1K 1M 1G
堆:
1.空间很大
2.手动申请,手动释放(还没看到)
字符串常量区:
"hello" //字符串常量
不能被修改 - 只读
全局区:
存放全局变量
代码区:
存放代码
程序 = 数据 + 代码
函数参数:
形式参数
实际参数
//形参 和 实参 规则:
1.个数相同
2.类型匹配
3.一一对应
数组元素作为函数参数:
数组名 能代表 整个数组 //给实参时,给定 数组名
1.数组 作为函数 参数 ,
形式上,保持一致,被调函数中 就可以 访问到主调函数中 数组的数据
一维整型数组作为函数参数
形参 写成数组的形式 同时需要 一个接受数组长度的形参
实参 传数组名,传数组长度
2.数组作为函数参数,
因为传的是数组名,而数组名是数组首元素的地址,所以相当于将数组空间的地址传给了被调函数,
而被调函数,通过数组下标运算,可以直接访问到了主调函数中对应数组空间的数据。
也就是说,数组传参的这种方式,可以实现,被调函数修改主调函数中的数据
注:
函数test:void test(int a[ ])其中a[ ]可替换为a[1],a[2],……a[n],因为编译器把这些都看做int *a
调用:test(a),这里只能写a,写a[0]之类会发生段错误,因为a[0]一般的值(例如0,1)会访问到不该访问的内存,
但是,如果写test(&a[4]),此时也可以运行,但是该数组的首元素为a[4],也就是说,如果此时数组长度为10,传入的的第6个元素就是本来的第10个元素,如果我要调用后面的元素(第7个,第8个),必然会产生越界问题,但是编译器不会报错(段错误)
特殊的:访问元素值的写法:
a[0]和[0]a一样,类似与加法1+2与2+1的区别
汉诺塔:
需求;
有一个老和尚想把64个盘子从A座移动到C座,
但每次只允许移动一个盘,且在移动过程中3个座上都始终保持大盘在下,
小盘在上。在移动过程中可以利用B座。
【问题】:
要求编程输出移动的步骤。(盘子个数可以动态指定)
思路:
问题n
|--问题n-1 与 n
|--问题n-2
|---
...结束条件
hanoi(64)
|---hanoi(63)
|---hanoi(62)
|---
...
hanoi(1)
也就是说:可以看成:起始柱'A',辅助柱'B',目标柱'C'
拿没我64个盘子,先把63个移到B,此时A剩下1个(最大的),把这个盘子从A移到C,同理把63拆成62,直到拆到1,直接放到C中
#include <stdio.h>
void move(unsigned char A,unsigned char B)
{
printf("%c-->%c\n",A,B);
}
//起始柱 //辅助柱 //目标柱
void hanoi(int n,unsigned char A,unsigned char B,unsigned char C)
{
if(n==1)
{
move(A,C);
}
else
{
hanoi(n-1,A,C,B);
move(A,C);
hanoi(n-1,B,A,C);
}
}
int main()
{
int n;
char A='A',B='B',C='C';
scanf("%d",&n);
hanoi(n,A,B,C);
return 0;
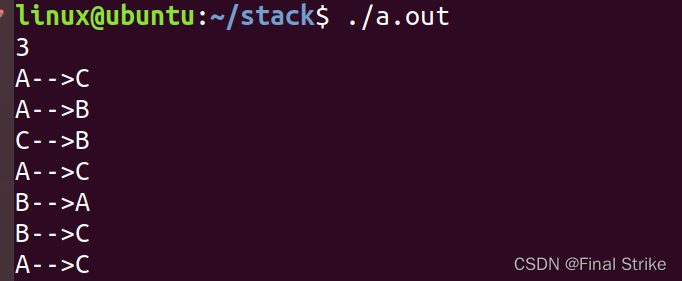
}3个盘子时的结果:
-->递归的思想:
1.递推公式,找出n-1项(可能有n-2,甚至更多)与第n项的关系
2.结束条件:找到结束条件(一般是n=1时,递归的结果)