【强化学习】马尔科夫性李宏毅蘑菇书第二章

本文主要针对强化学习中所需求的马尔科夫决策过程进行详解，讨论马尔科夫性到底是什么，为什么强化学习需要环境有马尔科夫性，马尔科夫奖励过程和马尔可夫决策过程是怎么做的，一共四个方面给具有一定基础知识的读者介绍强化学习。

主要参考李宏毅的蘑菇书，在线阅读链接。
感谢王琦等人编写的网站。
王琦，杨毅远，江季，Easy RL：强化学习教程，人民邮电出版社，https://github.com/datawhalechina/easy-rl, 2022.

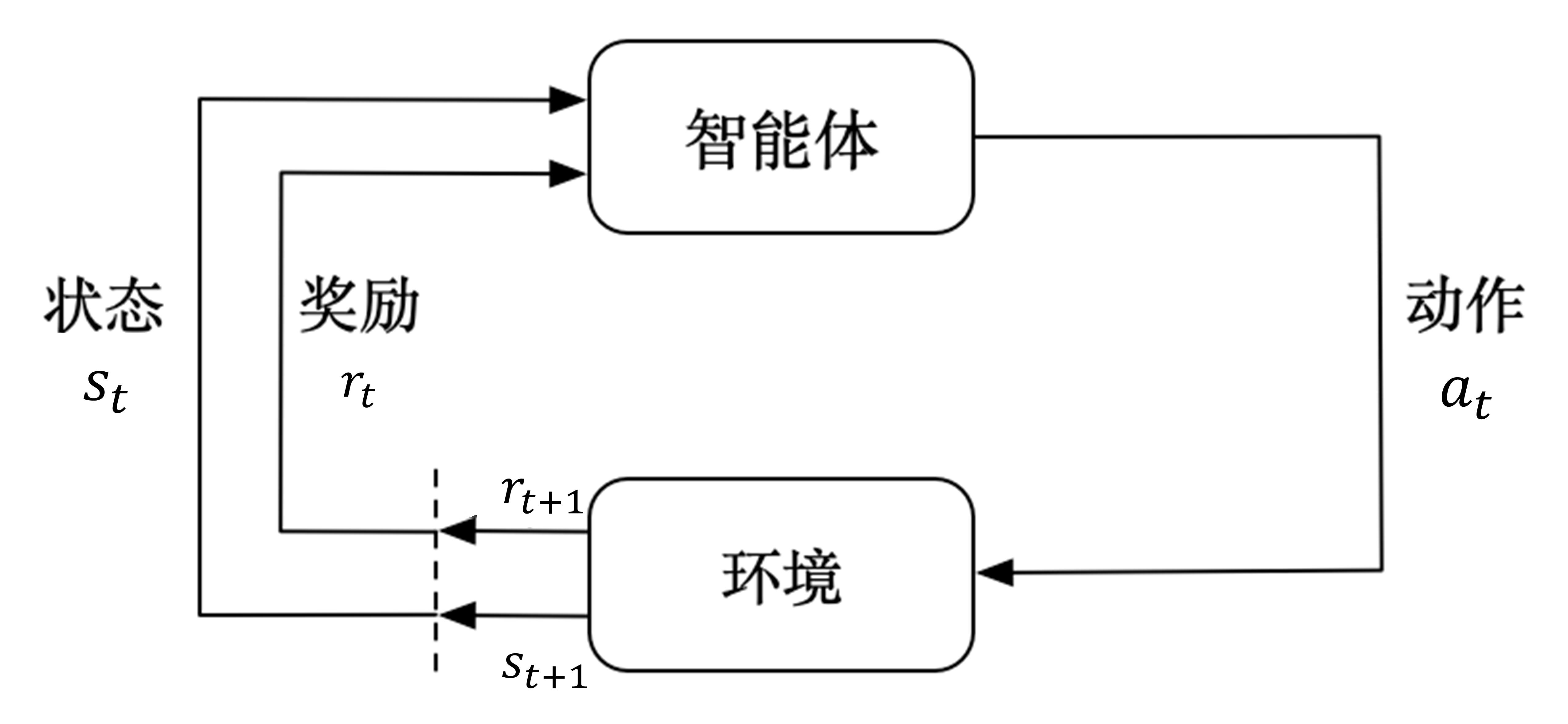
上文介绍了强化学习是什么，复习一下，强化学习主要使用智能体与环境进行交互进而学习。
智能体与环境交互的过程为：智能体得到环境的状态后，它会采取动作，并把这个采取的动作返还给环境。
环境对智能体反馈的过程为：环境得到智能体的动作后，它会进入下一个状态，把下一个状态传给智能体。

马尔科夫性

强化学习过程可以使用马尔科夫决策过程来表示，所以马尔可夫决策过程是强化学习的基本框架。

智能体和环境的交互
但是至此我们还是不知道马尔科夫性是什么呢，我们只知道强化学习需要这个，因此笔者寻找了一本统计书籍上关于马尔科夫性的定义：

笔者认为马尔科夫性可以通俗的理解为：当前状态和之前没有关系（相互独立），即当前这个状态只是从上一个状态一定概率得到的，与其他的一点关系都没有，这被称为马尔科夫性。

如果某一个过程满足马尔可夫性质，那么未来的转移与过去的是独立的，它只取决于现在。马尔可夫性质是所有马尔可夫过程的基础。
马尔可夫过程（Markov process，MP）以及马尔可夫奖励过程（Markov reward process，MRP）都具有马尔科夫性，两者都对强化学习很有用。通过与这两种过程的比较，可以更容易理解马尔可夫决策过程。

马尔可夫过程是一组具有马尔可夫性质的随机变量序列 $s_1,\cdots,s_t$ ,其中下一个时刻的状态 $s_{t+1}$ 只取决于当前状态 $s_t$ 。我们设状态的历史为 $h_t= \left\{s_1,s_2,s_3,\ldots,s_t\right\}$ 包含了之前的所有状态),则马尔可夫过程满足条件:

$p\left(s_{t+1}\mid s_{t}\right)=p\left(s_{t+1}\mid h_{t}\right)$

为什么强化学习需要马尔科夫性

首先我们从马尔科夫性的原因上了解，马尔科夫性是指下一个时刻的状态 $s_{t+1}$ 只取决于当前状态 $s_t$ ，那没有马尔科夫性的过程可以分为两种：一是当前状态 $s_{t+1}$ 与前一个状态 $s_t$ 无关，二是当前状态 $s_{t+1}$ 不仅与前一个状态 $s_t$ 有关，还与之前的某个状态 $s_{t-i}$ 有关。

先考虑第一种，如果当前状态 $s_{t+1}$ 与前一个状态 $s_t$ 无关，那么强化学习就不太好进行更新，无论是他与前面那个状态有关还是无关，距离的远就意味着开销很大，而且没有具体相关的关系，就可能无法顺利进行迭代。就算是只和上上个状态相关，决策过程的确定会麻烦不少，而且是反直觉的，这种或许可以用其他方法进行挖掘，但是强化学习不适用。

第二种是如果当前状态 $s_{t+1}$ 不仅与前一个状态 $s_t$ 有关，还与之前的某个状态 $s_{t-i}$ 有关，那么这种情况下的决策过程很难，且泛化能力不佳，因为无法知道与哪个有关系，书写奖励函数等数学公式会变得异常复杂，大大增加了计算开销。

综合考虑，强化学习需要马尔科夫性的原因主要基于以下几点：

简化决策过程：马尔科夫性假设下一个状态的概率仅依赖于当前状态和当前动作，而与之前的状态历史无关。这种假设简化了决策过程，使得智能体只需要关注当前状态和可能的动作，而不需要考虑复杂的历史信息。
数学模型的可解性：在强化学习中，马尔科夫决策过程（MDP）是一个核心概念。MDP提供了一个数学框架，用于建模决策制定的问题。马尔科夫性使得MDP的状态转移概率可以用数学方式精确描述，从而可以使用动态规划、蒙特卡洛方法或时序差分学习等算法来求解最优策略。
优化策略：强化学习的目标是找到最优策略，使得长期累积的预期奖励最大化。马尔科夫性允许智能体基于当前状态和动作来预测未来的状态和奖励，从而优化其策略。
处理不确定性：在现实世界中，环境通常是不确定的，马尔科夫性允许智能体在这种不确定性中通过试错学习最优策略，逐步提升性能并逼近最优解。
泛化能力：马尔科夫性提供了一种泛化的方式来处理各种不同的环境和任务，因为它不依赖于具体环境的细节，而只关注状态之间的转移概率和奖励。

综上所述，马尔科夫性是强化学习中一个关键的假设，它使得问题建模、策略学习和优化变得更加可行和有效。

马尔科夫奖励过程

马尔可夫奖励过程（Markov reward process, MRP）是马尔可夫链加上奖励函数。在马尔可夫奖励过程中，状态转移矩阵和状态都与马尔可夫链一样，只是多了奖励函数（reward function）马尔科夫决策就是马尔科夫链的决策过程。

在马尔可夫奖励过程中，状态转移矩阵和状态都与马尔可夫链一样，只是多了奖励函数（reward function）。奖励函数 R 是一个期望，表示当我们到达某一个状态的时候，可以获得多大的奖励。这里另外定义了折扣因子 γ。如果状态数是有限的，那么 R 可以是一个向量。

这里由于是理解概念，所以公式需要去看原文书写。

这里有一个贝尔曼方程，就是用于计算回报的价值函数，就不详细讲了，有需要的可以看上面的链接。

马尔可夫决策过程

相对于马尔可夫奖励过程，马尔可夫决策过程多了决策（决策是指动作），其他的定义与马尔可夫奖励过程的是类似的。此外，状态转移也多了一个条件，变成了 $p\left(s_{t+1}=s^{\prime}\mid s_{t}=s,a_{t}=a\right)$ 未来的状态不仅依赖于当前的状态，也依赖于在当前状态智能体采取的动作。马尔可夫决策过程满足条件：
$p\left(s_{t+1}\mid s_t,a_t\right)=p\left(s_{t+1}\mid h_t,a_t\right)$
对于奖励函数，它也多了一个当前的动作，变成了 $R\left(s_t=s,a_t=a\right)=\mathbb{E}\left[r_t\mid s_t=s,a_t=a\right]$ 当前的状态以及采取的动作会决定智能体在当前可能得到的奖励多少。

策略定义了在某一个状态应该采取什么样的动作。知道当前状态后，我们可以把当前状态代入策略函数来得到一个概率。概率代表在所有可能的动作里面怎样采取行动，比如可能有 0.7 的概率往左走，有 0.3 的概率往右走，这是一个概率的表示。另外策略也可能是确定的，它有可能直接输出一个值，或者直接告诉我们当前应该采取什么样的动作，而不是一个动作的概率。假设概率函数是平稳的（stationary），不同时间点，我们采取的动作其实都是在对策略函数进行采样。

马尔可夫决策过程和马尔可夫过程/马尔可夫奖励过程的区别

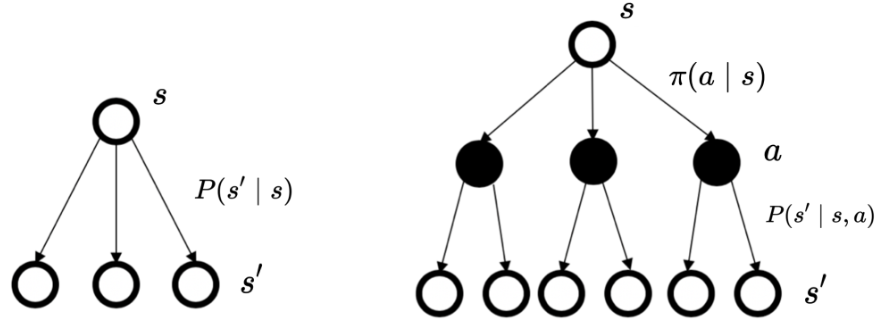
马尔可夫决策过程里面的状态转移与马尔可夫奖励过程以及马尔可夫过程的状态转移的差异如下图所示。马尔可夫过程/马尔可夫奖励过程的状态转移是直接决定的。比如当前状态是 s，那么直接通过转移概率决定下一个状态是什么。但对于马尔可夫决策过程，它的中间多了一层动作 a ，即智能体在当前状态的时候，首先要决定采取某一种动作，这样我们会到达某一个黑色的节点。到达这个黑色的节点后，因为有一定的不确定性，所以当智能体当前状态以及智能体当前采取的动作决定过后，智能体进入未来的状态其实也是一个概率分布。在当前状态与未来状态转移过程中多了一层决策性，这是马尔可夫决策过程与之前的马尔可夫过程/马尔可夫奖励过程很不同的一点。在马尔可夫决策过程中，动作是由智能体决定的，智能体会采取动作来决定未来的状态转移。
马尔可夫决策过程与马尔可夫过程/马尔可夫奖励过程的状态转移的对比
这里没有说策略评估，有需要还是去看原文，策略评估就是看当前的决策过程大概可以得到多少的奖励。

一个例子

这个是斯坦福大学的一个动态的例子。

总结

原文用这些进行了总结：使用动态规划算法来解马尔可夫决策过程里面的预测和控制，并且采取不同的贝尔曼方程。对于预测问题，即策略评估的问题，我们不停地执行贝尔曼期望方程，这样就可以估计出给定的策略，然后得到价值函数。对于控制问题，如果我们采取的算法是策略迭代，使用的就是贝尔曼期望方程；如果我们采取的算法是价值迭代，使用的就是贝尔曼最优方程。

动态规划算法

然后我也上传了在花书中第十六章，强化学习的ppt和课后习题，欢迎关注我免费下载。