目录
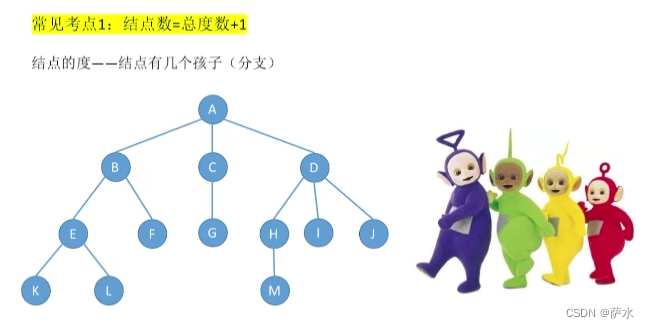
1、结点数 = 总度数 + 1（结点的度 --- 结点有几个孩子（分支））
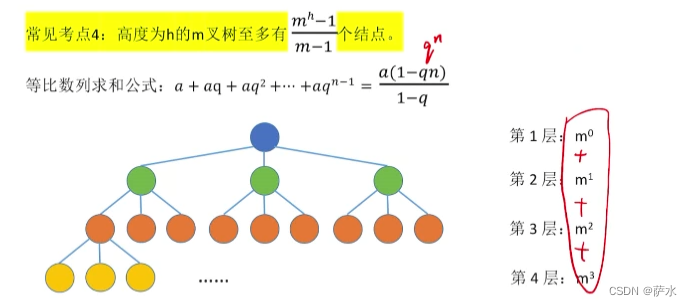
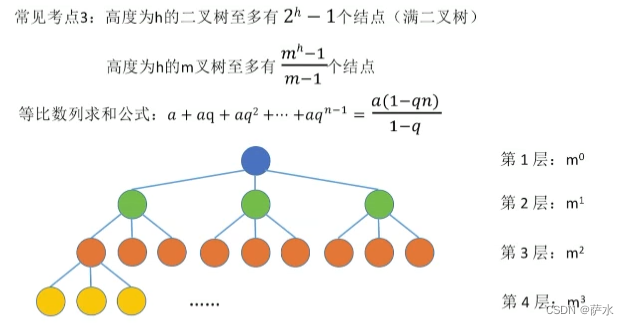
4、高度为 h 的 m 叉树至多有 （m**h - 1）/ （m - 1）个结点
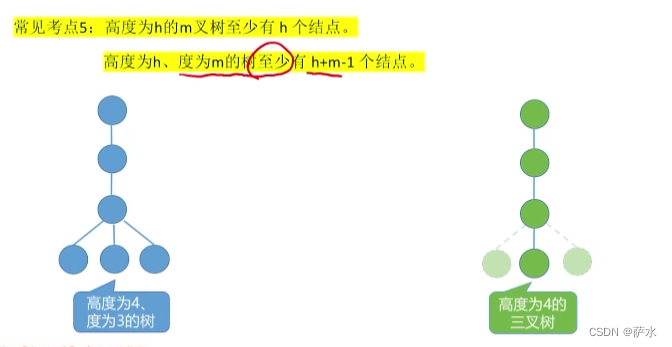
5、高度为 h 的 m 叉树至少有 h 个结点；高度为 h 、度为 m 的树至少有 h+m-1个结点
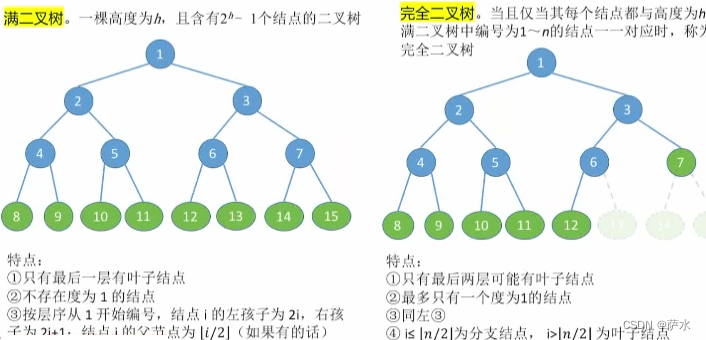
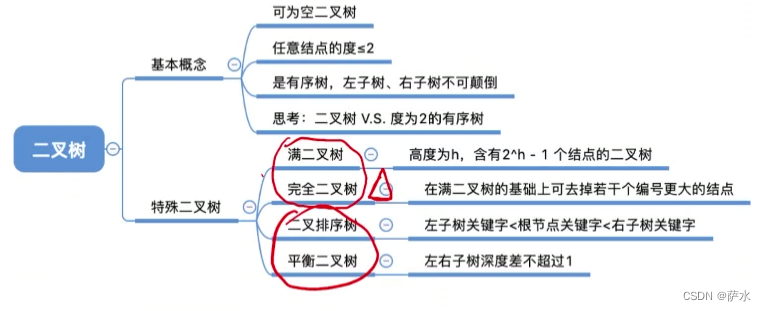
（1）满二叉树。一颗高度为h，且含有 2**h - 1个结点的二叉树
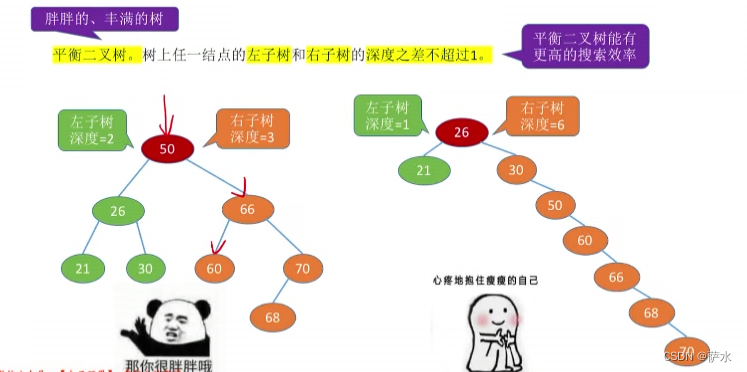
（4）平衡二叉树 。任意结点的 左子树 与 右子树 的 深度之差 不超过1。左边小，右边大。
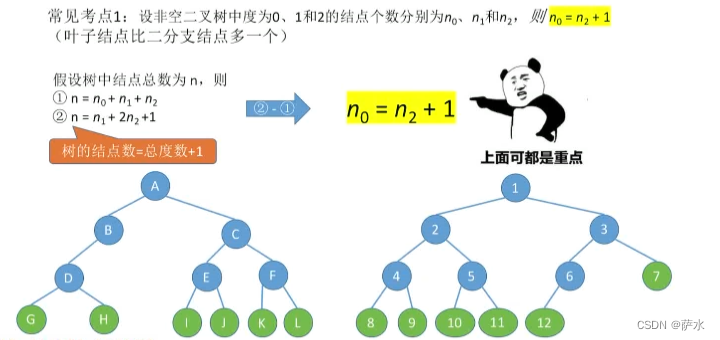
1、 度为0结点个数 = 度为2结点个数 + 1（N0 = N2 + 1）
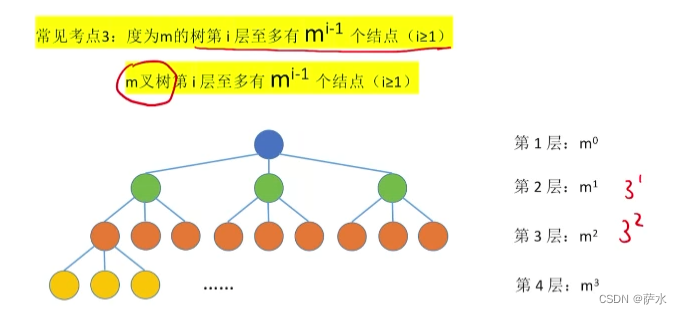
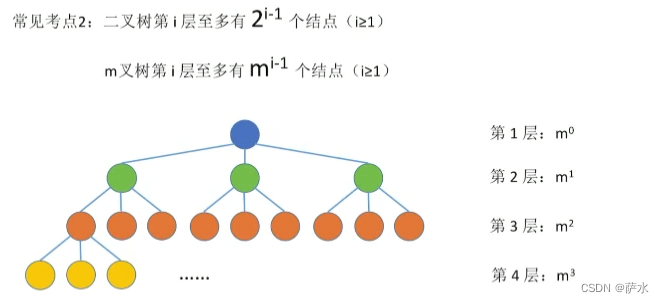
2、二叉树第 i 层 至多有 2**（i - 1）个结点（i >= 1）；m叉树第 i 层至多有 m**（i - 1）
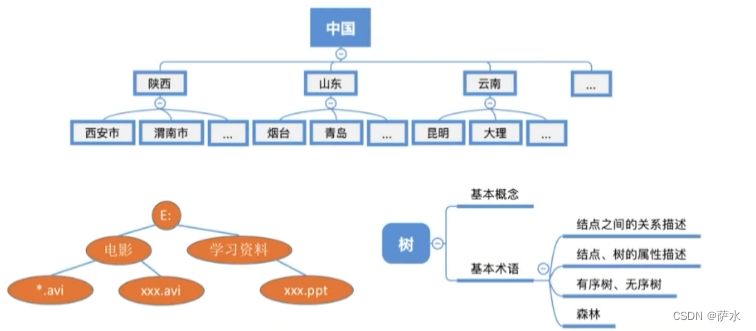
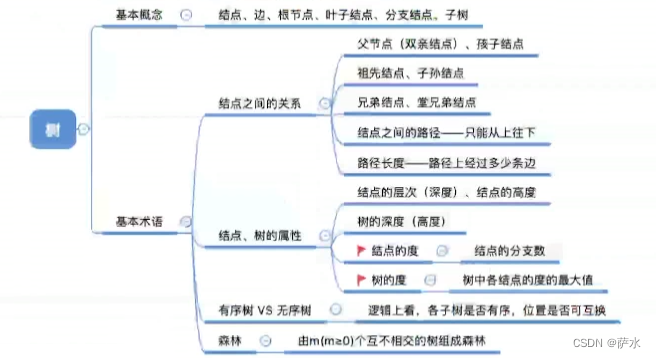
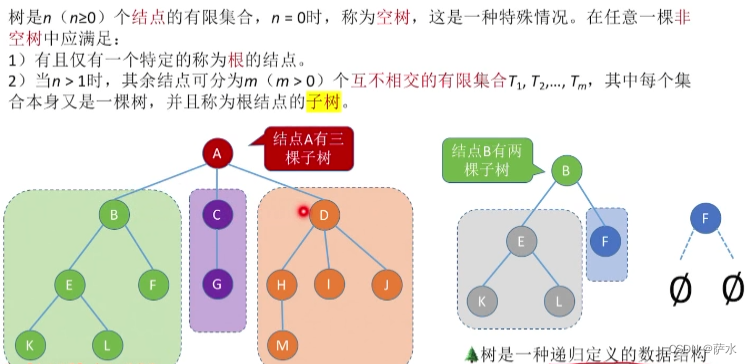
一、树的基本概念术语
知识总览
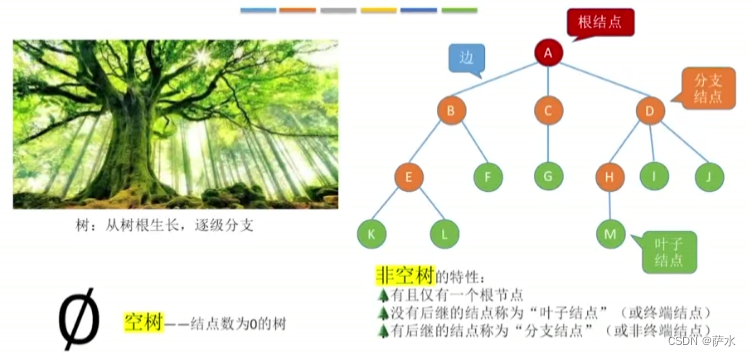
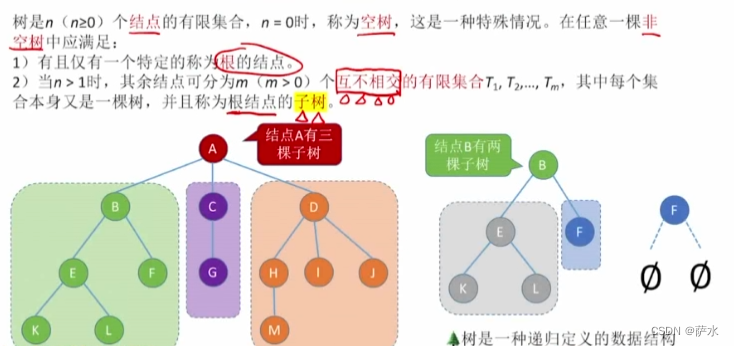
1、基础概念
【除了根节点之外，任何一个结点都有且仅有一个前驱】
2、树逻辑结构的应用
3、结点之间的关系描述
4、结点、树的属性描述
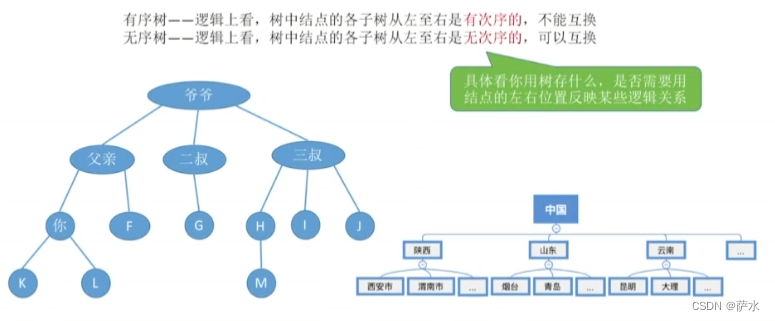
5、有序树 V.S 无序树
6、树 VS 森林
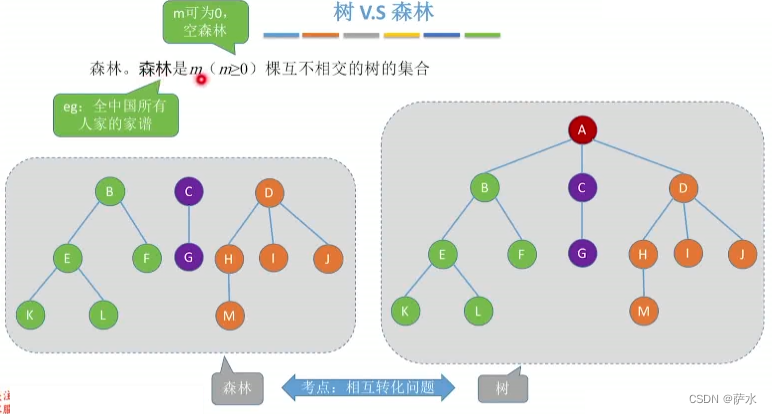允许空树，也允许空森林！！！
7、小结
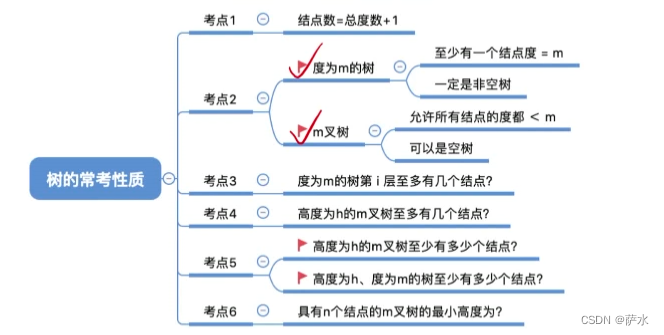
二、树的常考性质
1、结点数 = 总度数 + 1（结点的度 --- 结点有几个孩子（分支））
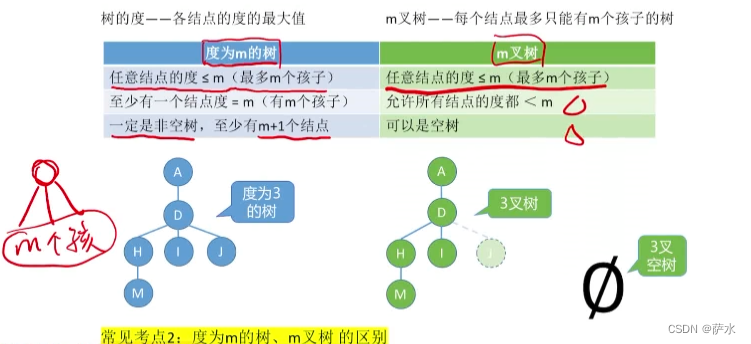
2、度为m的树、m叉树的区别
3、度为m的树，第 i 层至多有m**（i-1）个结点
4、高度为 h 的 m 叉树至多有 （m**h - 1）/ （m - 1）个结点
5、高度为 h 的 m 叉树至少有 h 个结点；高度为 h 、度为 m 的树至少有 h+m-1个结点
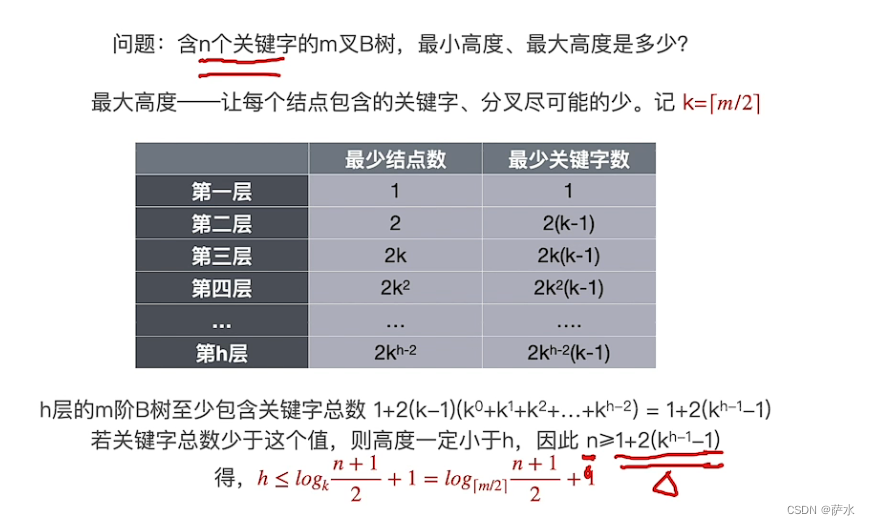
6、具有 n 个结点的 m 叉树的最小高度为
7、小结
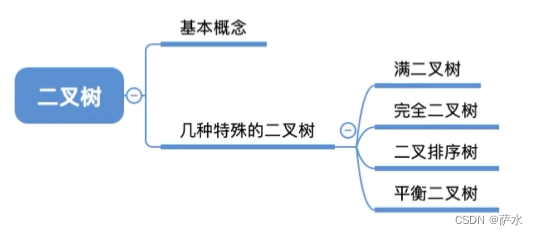
三、二叉树的基本概念及术语
知识总览
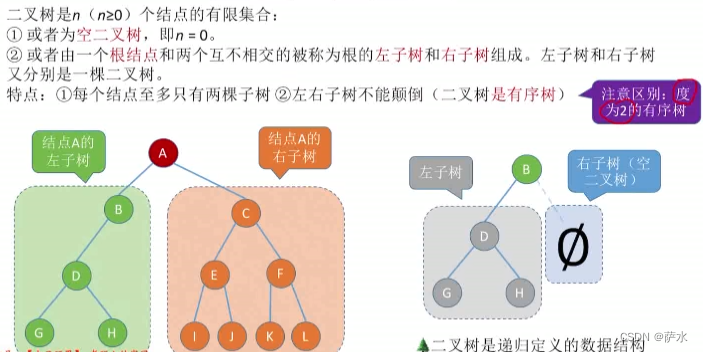
1、二叉树基本概念
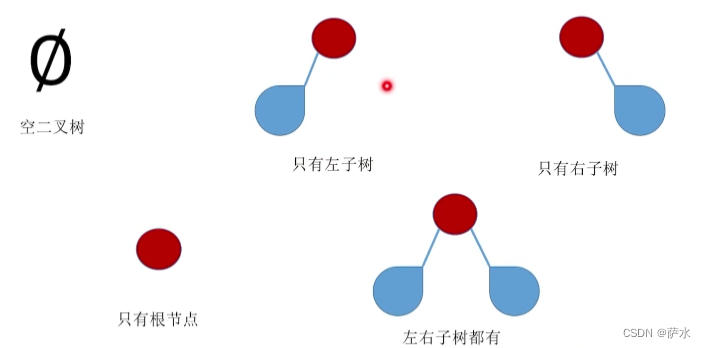
2、二叉树的五种状态
3、几种特殊的二叉树
（1）满二叉树。一颗高度为h，且含有 2**h - 1个结点的二叉树
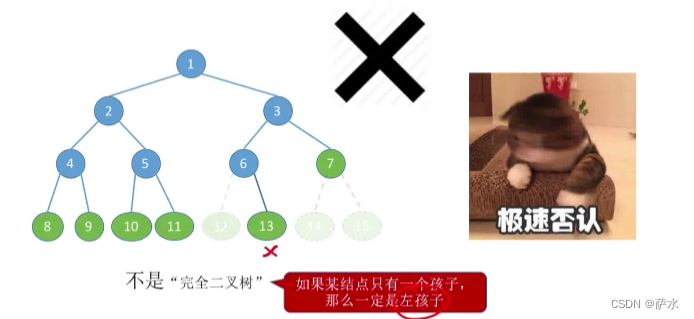
（2）完全二叉树。每个结点的编号与满二叉树一 一对应。
【从左至右，依次编号，存在顺序，不可颠倒】
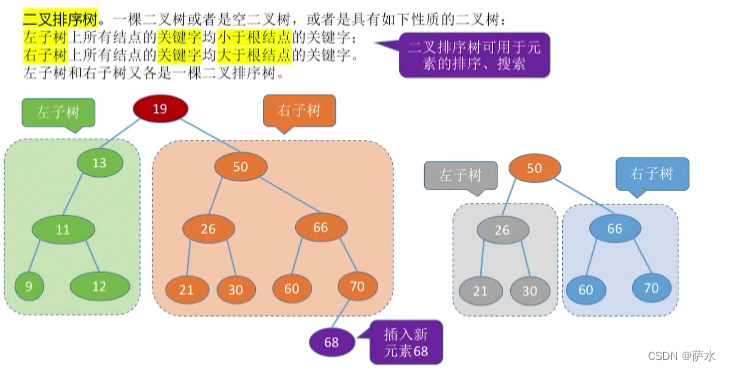
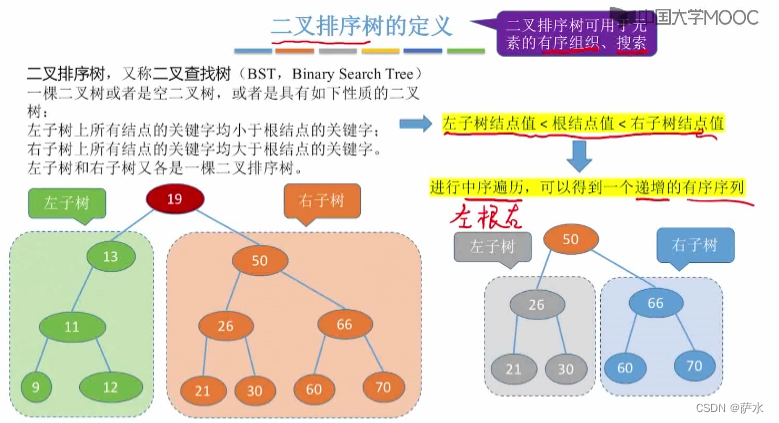
（3）二叉排序树。左边小，右边大。
（4）平衡二叉树 。任意结点的 左子树 与 右子树 的 深度之差 不超过1。左边小，右边大。
4、小结
四、二叉树的常考性质
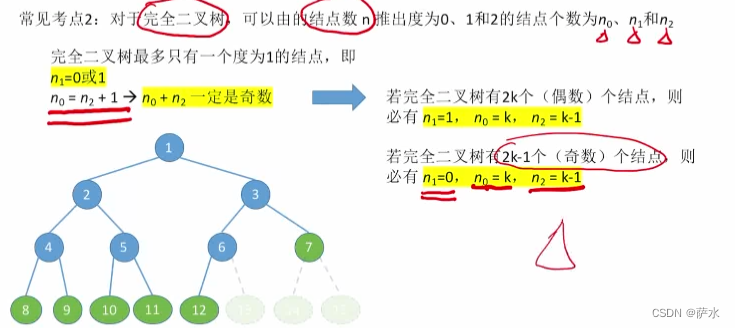
1、 度为0结点个数 = 度为2结点个数 + 1（N0 = N2 + 1）
2、二叉树第 i 层 至多有 2**（i - 1）个结点（i >= 1）；m叉树第 i 层至多有 m**（i - 1）
3、高度 h ，二叉树结点 2**h - 1
4、完全二叉树的常考性质
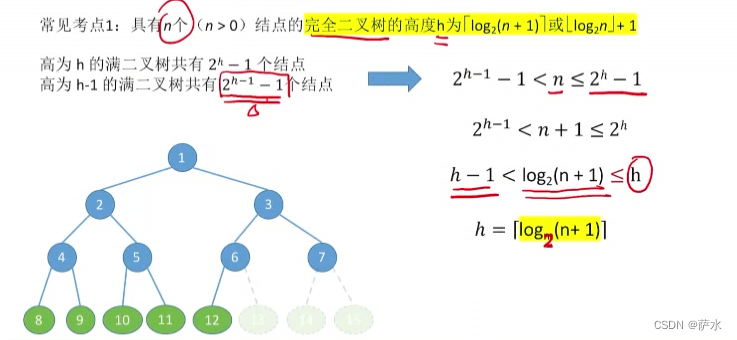
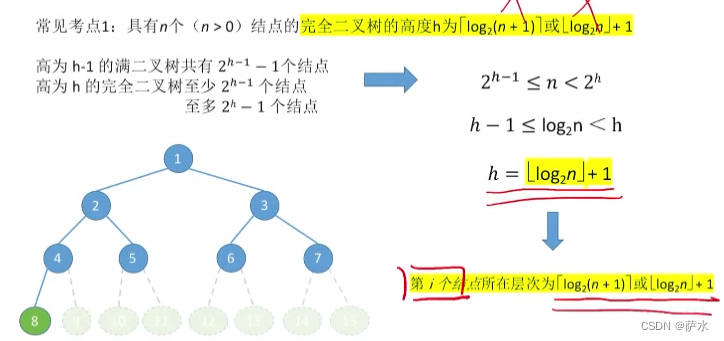
（1）n（n>=0）结点，完全二叉树的高度 h 为 log2（n+1）或 log2n +1
（2） 结点奇偶数
5、小结
五、二叉树的存储结构
知识总览
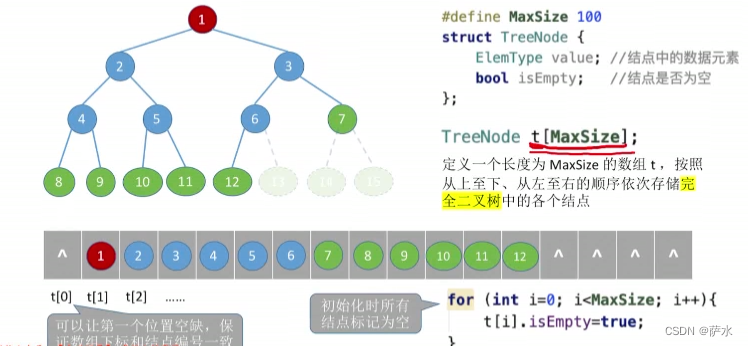
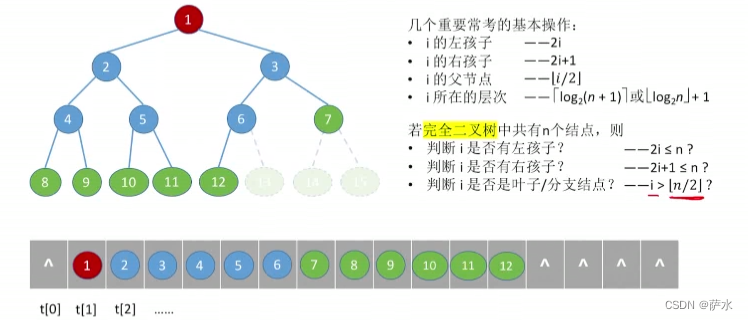
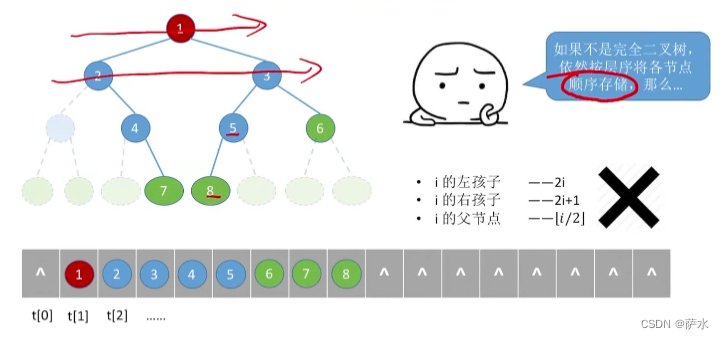
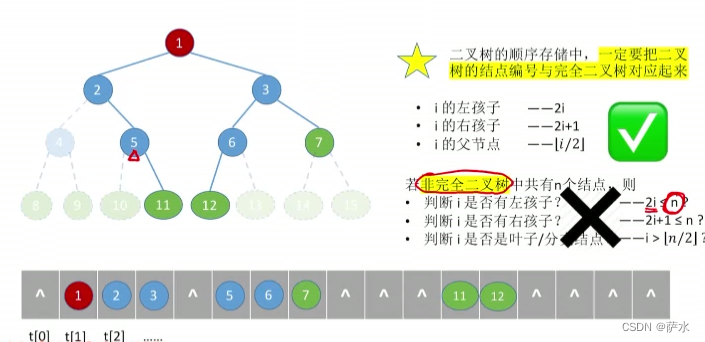
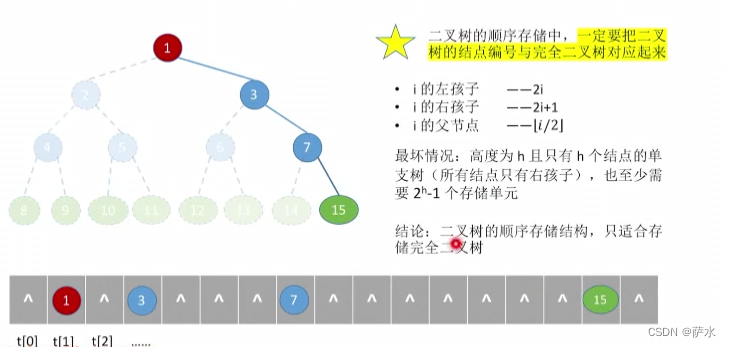
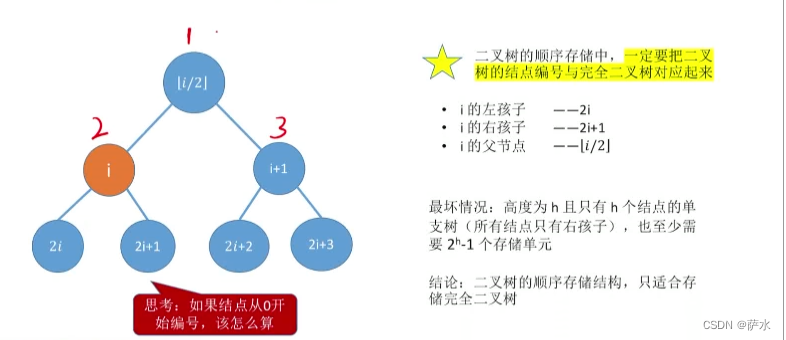
1、二叉树的顺序存储
【结论】二叉树的顺序存储结构，只适合存储完全二叉树！！！！！！
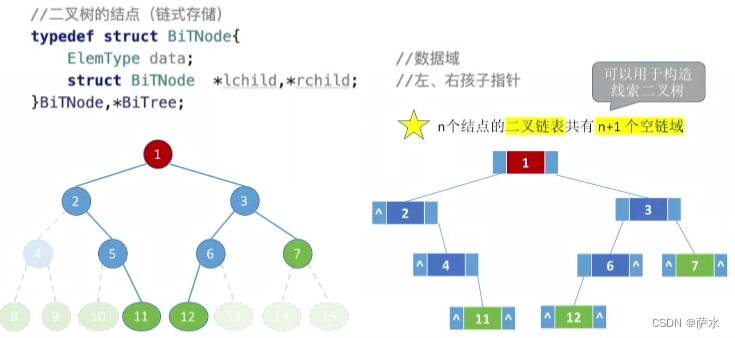
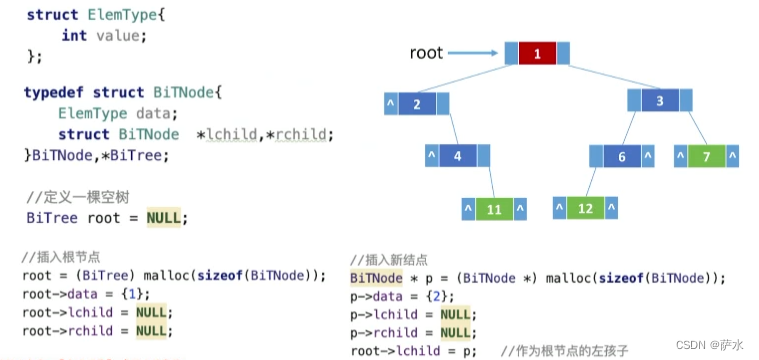
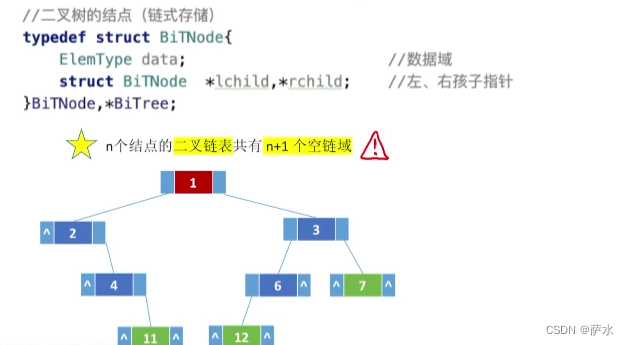
2、二叉树的链式存储
初始化、构建链式二叉树
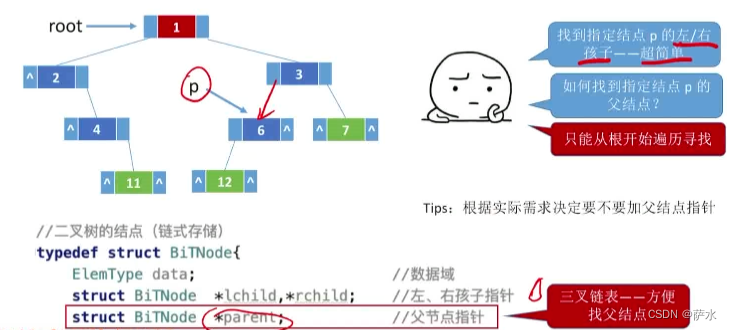
向下有左右指针，向上可以设定一个父节点指针
3、小结
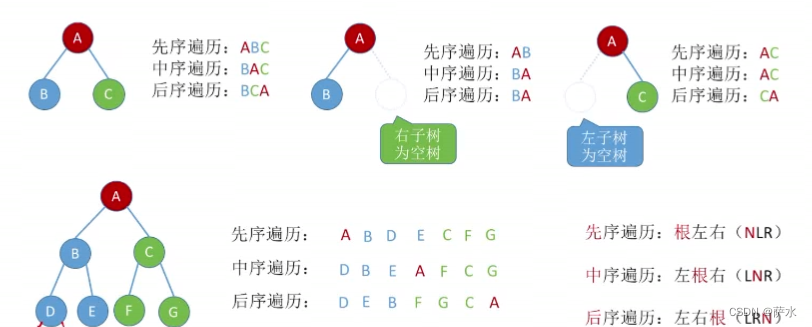
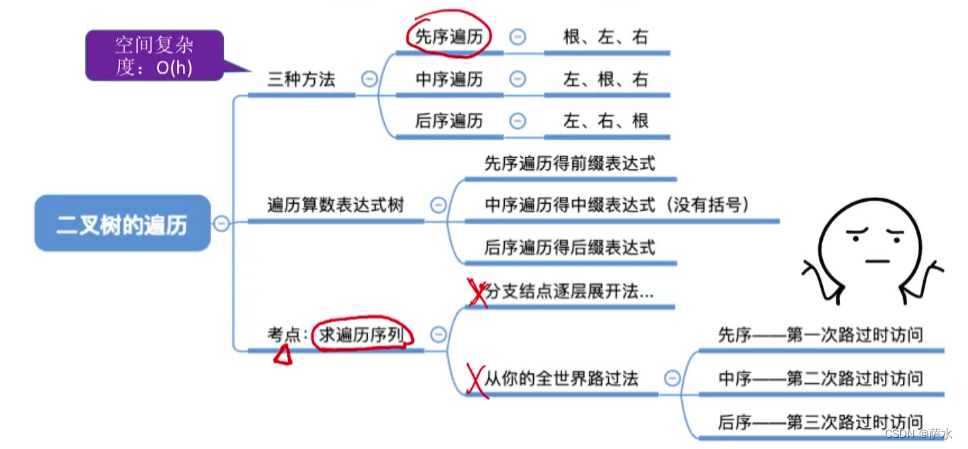
六、二叉树（先/中/后序遍历）
知识总览
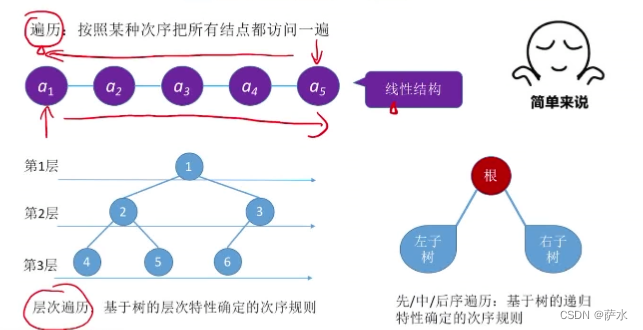
1、什么是遍历
按照某种次序把所有结点都访问一遍
2、 二叉树的遍历
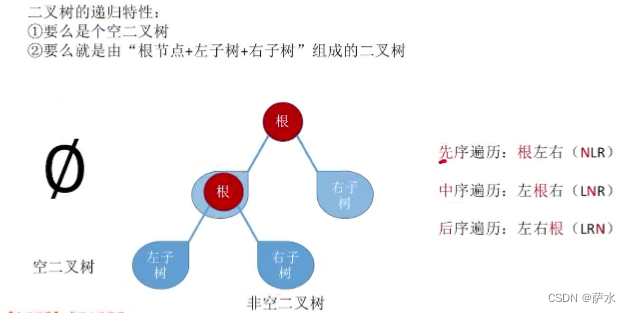
（1）二叉树递归特性
（2）分支结点逐层展开法
3、遍历代码实现
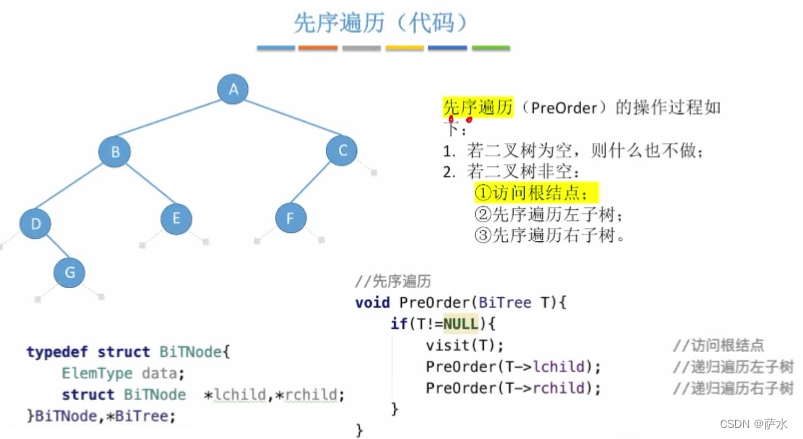
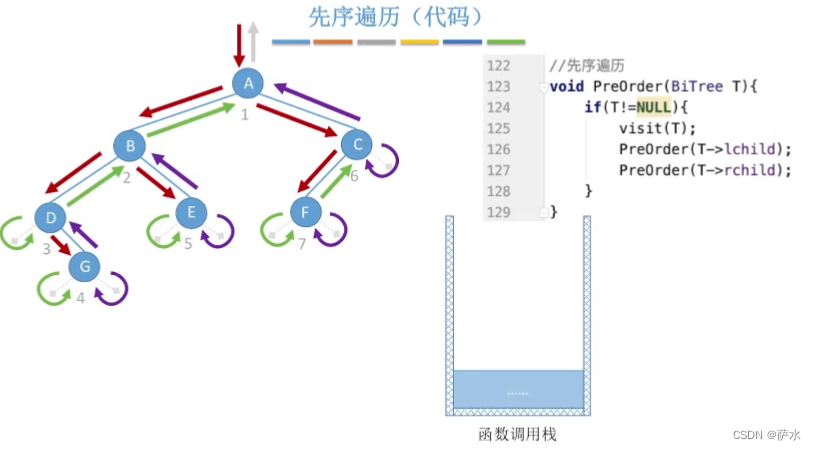
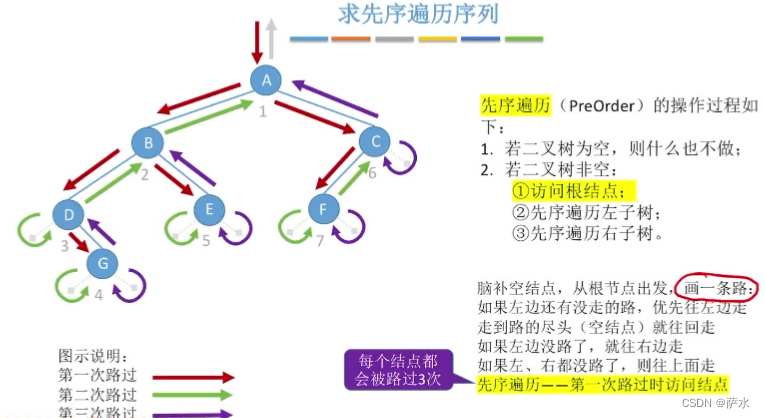
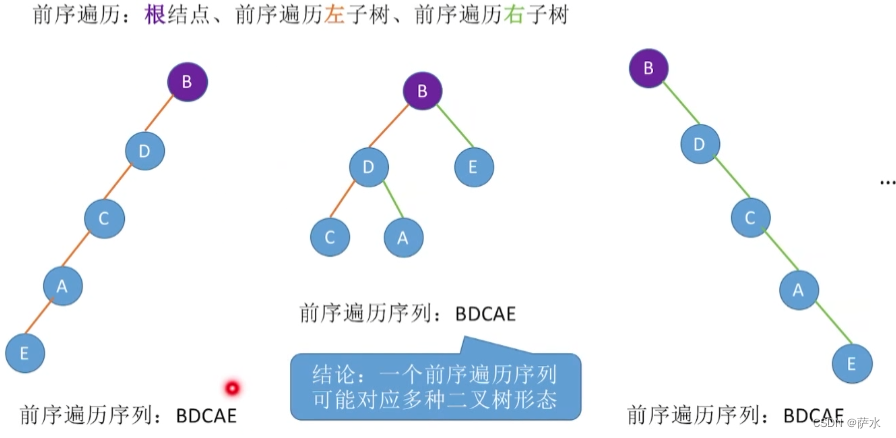
（1）先序遍历
空间复杂度 = O（h+1）=O（h）【h：树的高度】
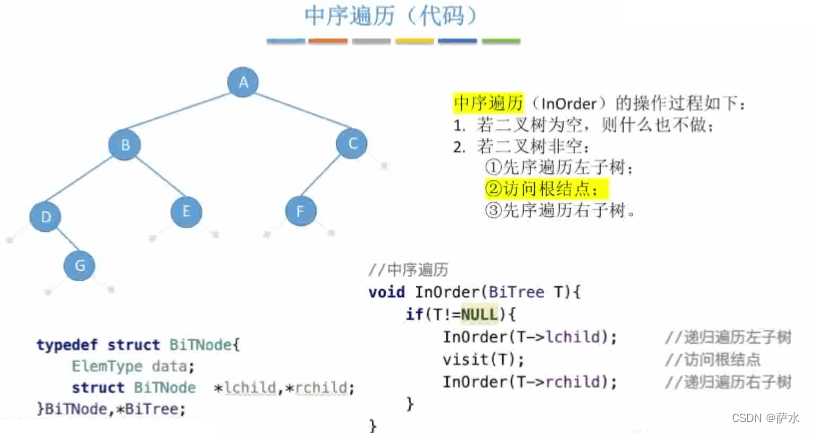
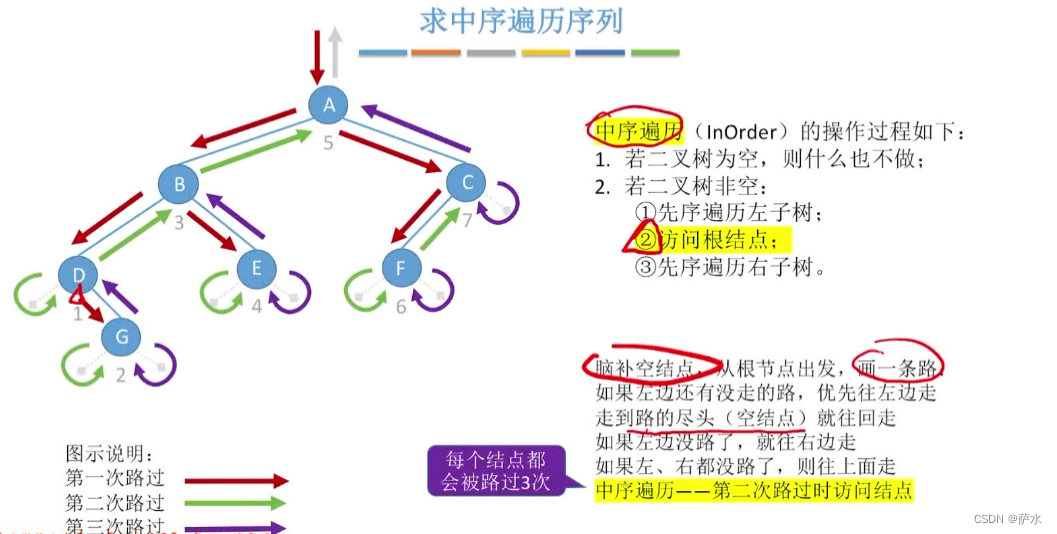
（2）中序遍历
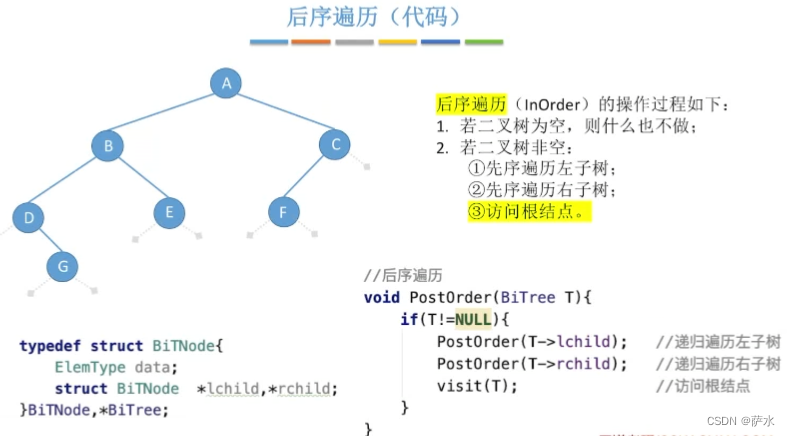
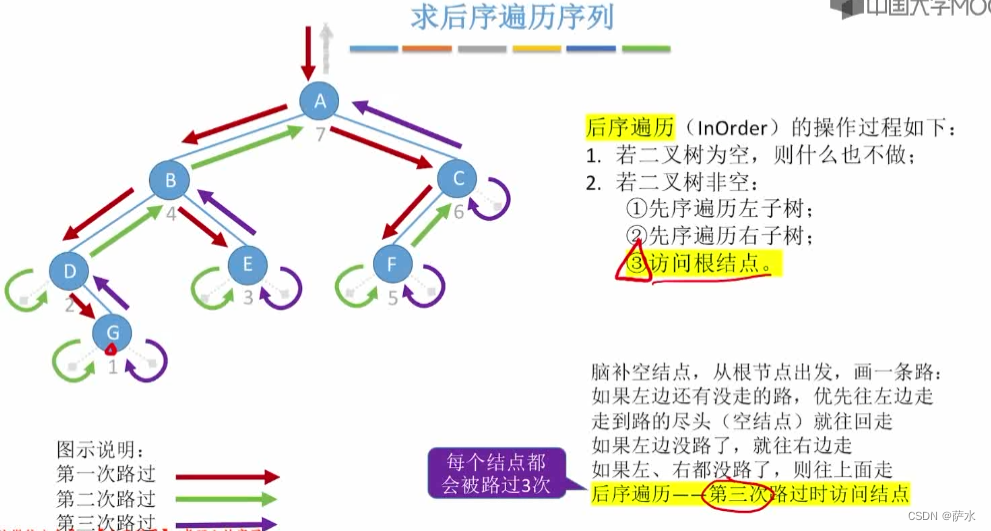
（3）后序遍历
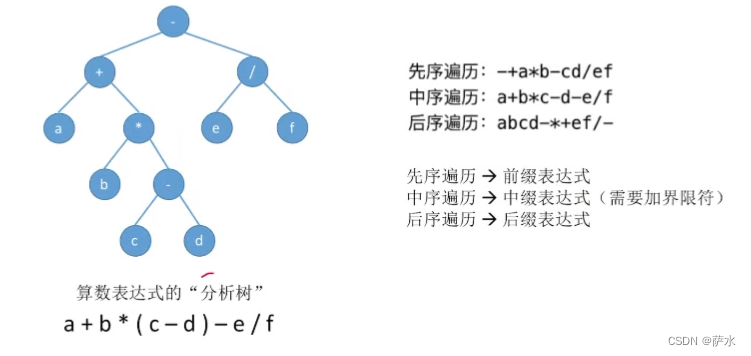
4、应用
5、小结
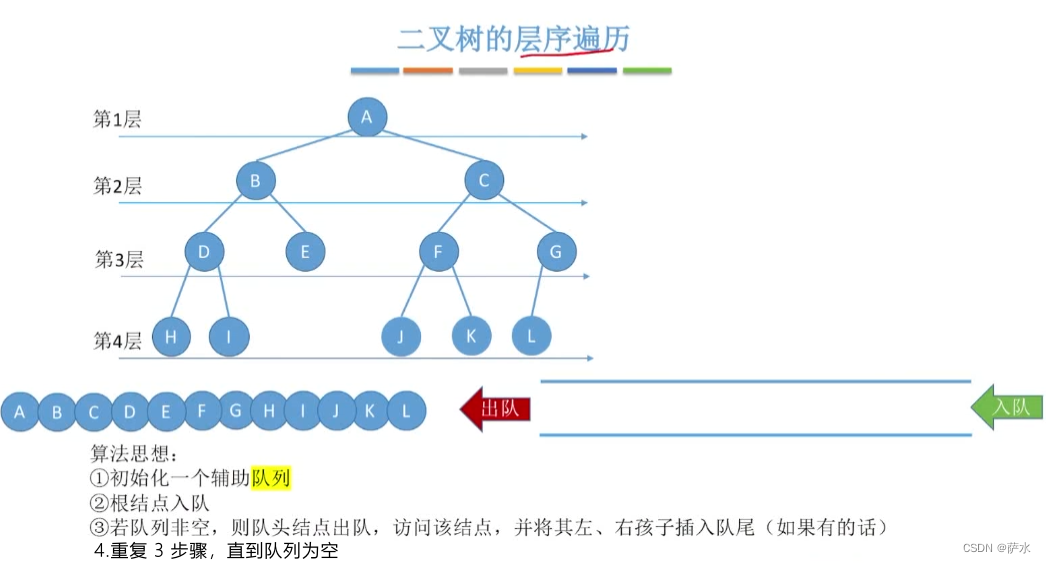
七、二叉树（层序遍历）
代码实现
小结
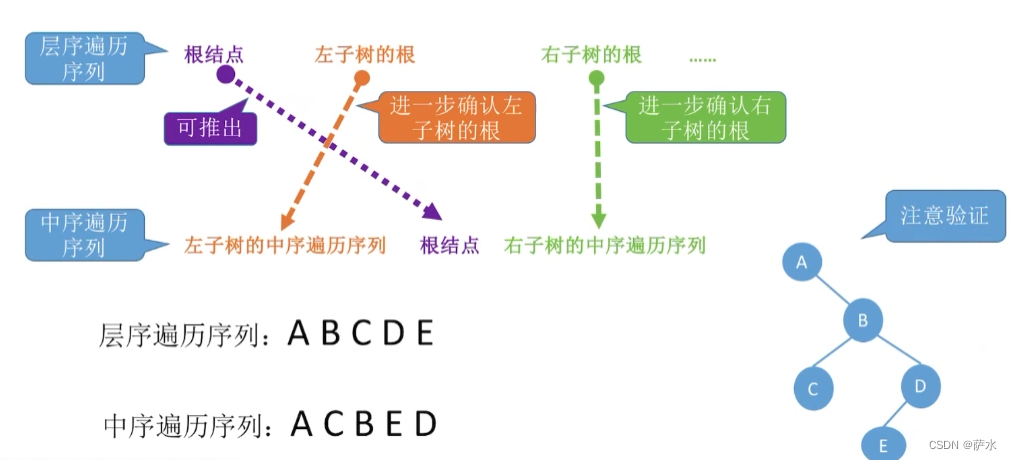
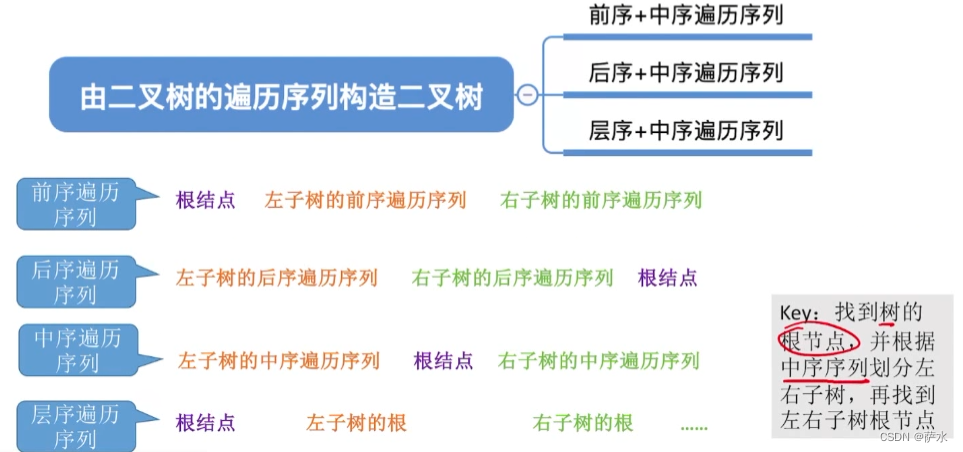
八、由遍历序列构造二叉树
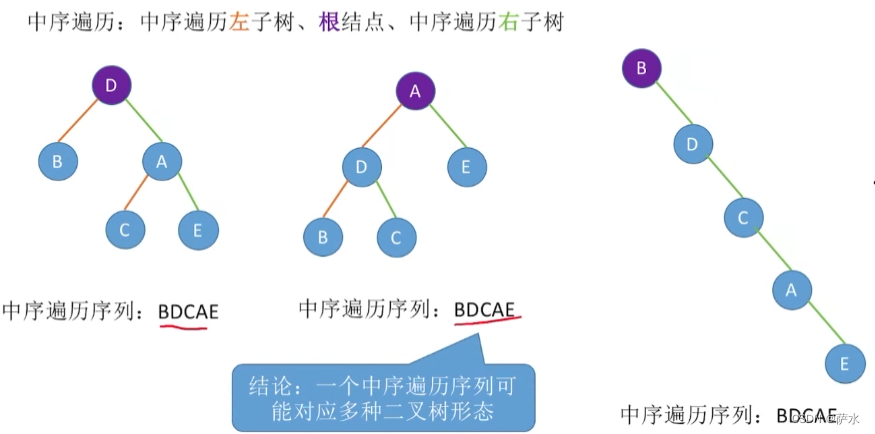
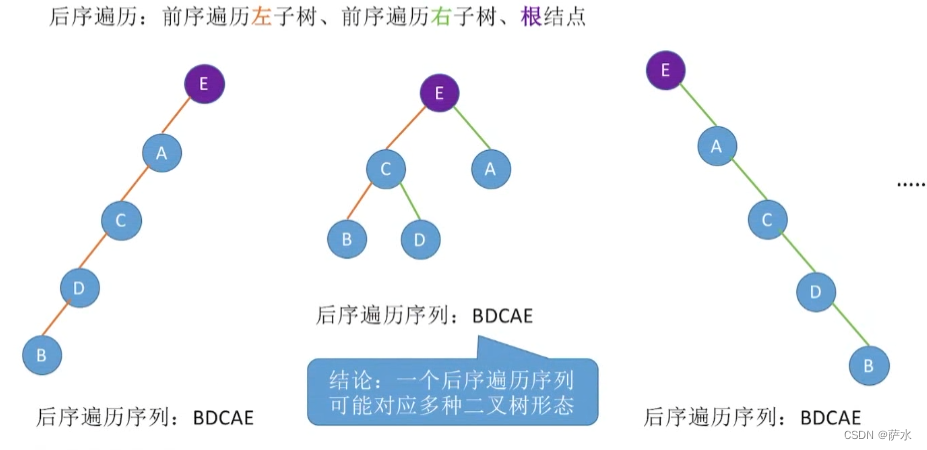
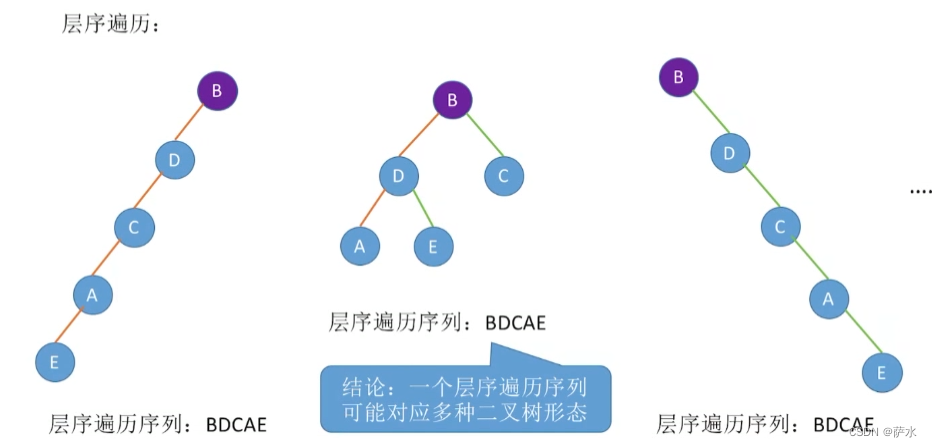
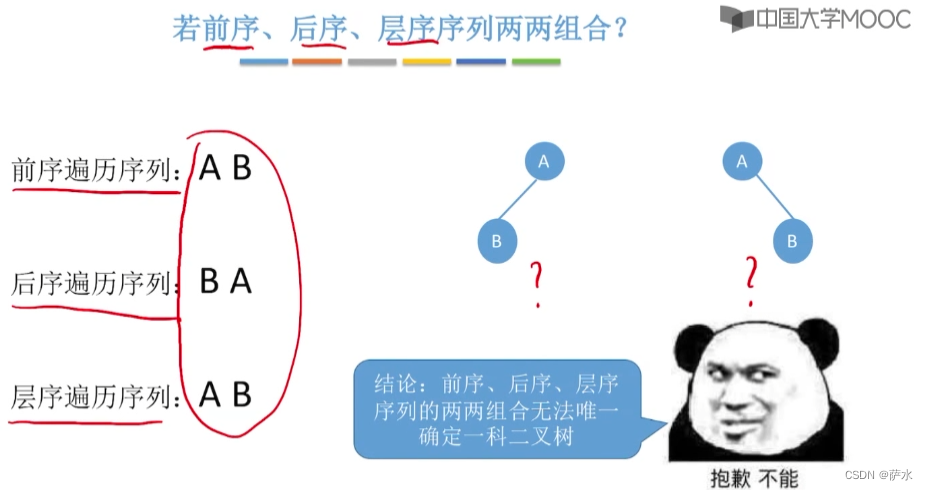
1、【结论】前中后、层遍历序列可能对应多种二叉树形态
2、由遍历序列组合构造二叉树
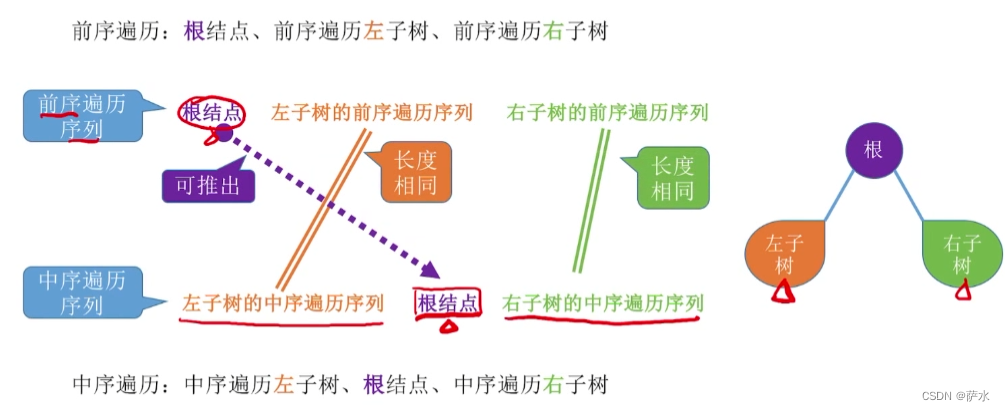
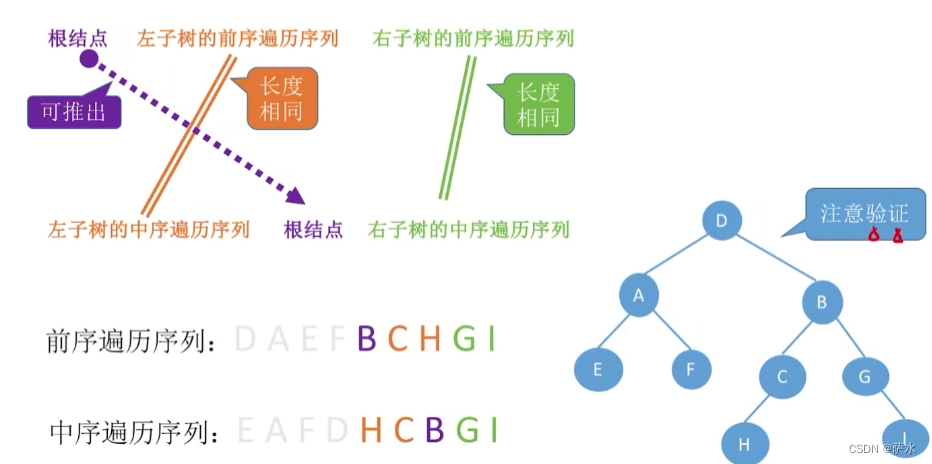
（1） 前序 + 中序
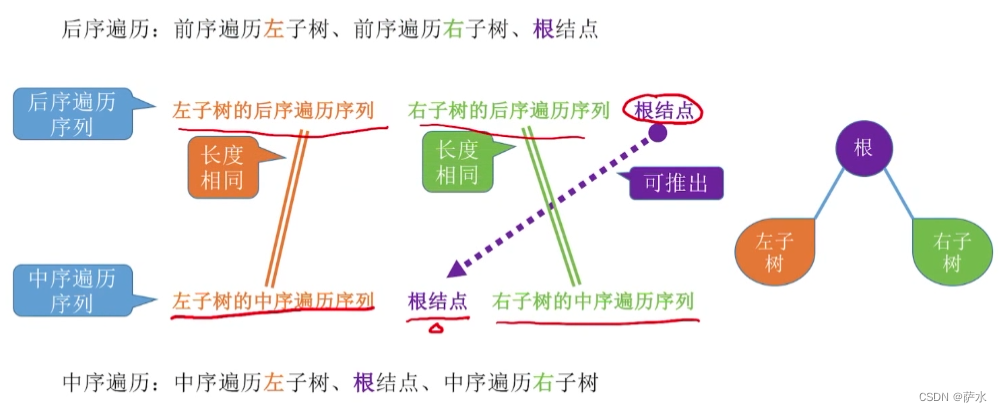
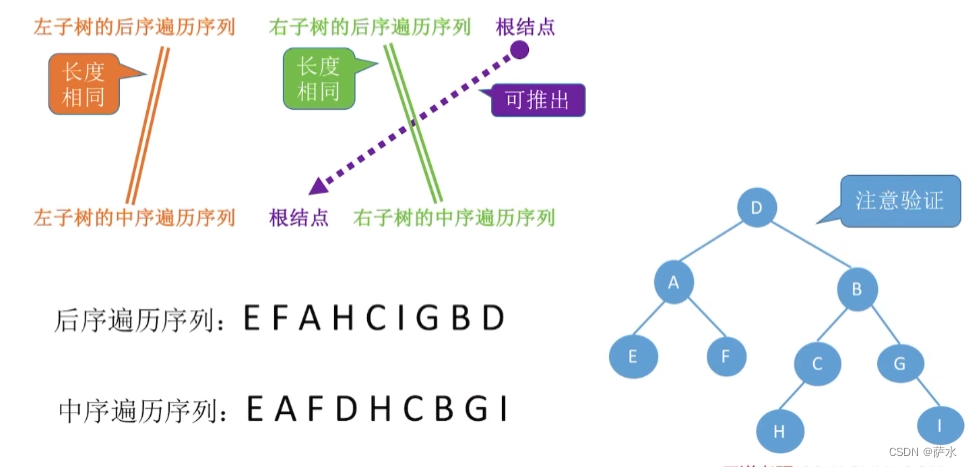
（2）后序 + 中序
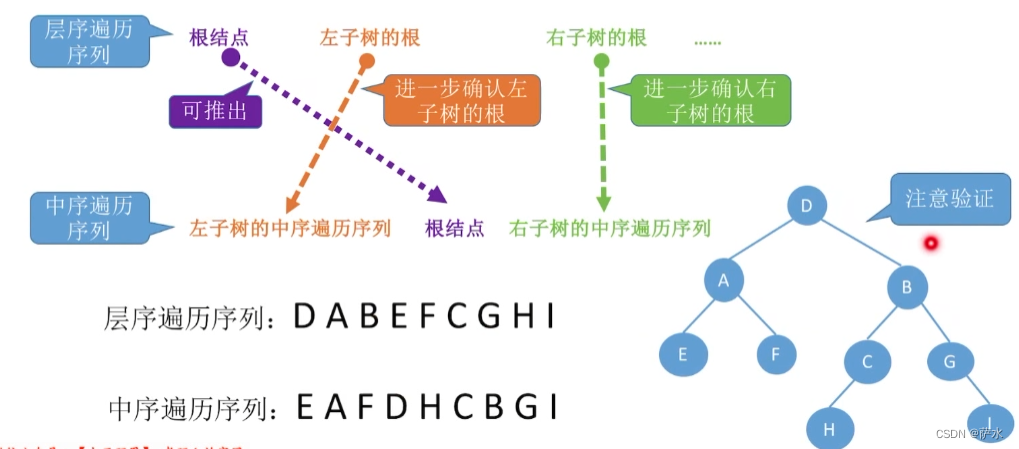
（3）层序 + 中序
3、小结
必须要有中序序列才能确定！！！！！！！！！！！！！
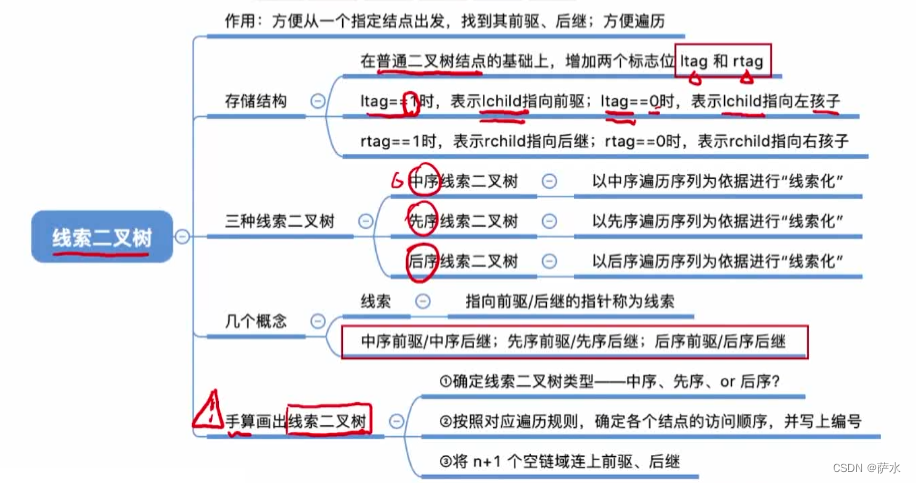
九、线索二叉树
知识总览
1、作用
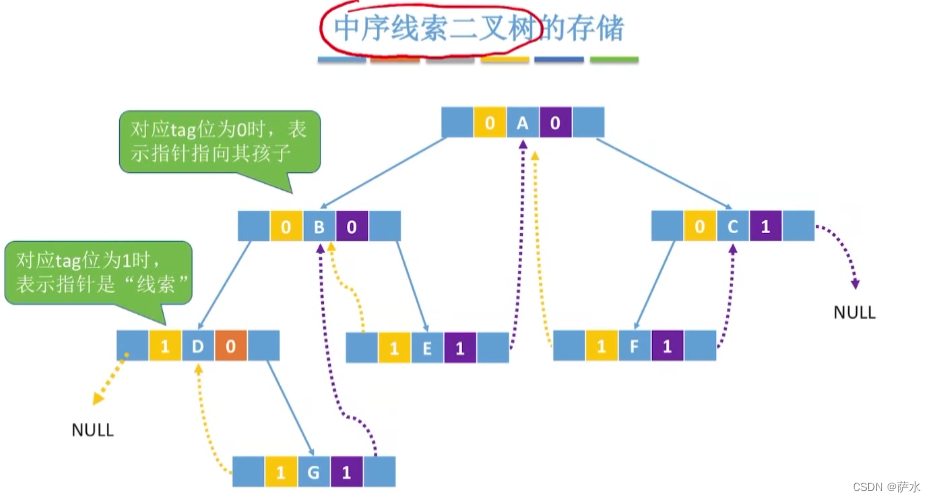
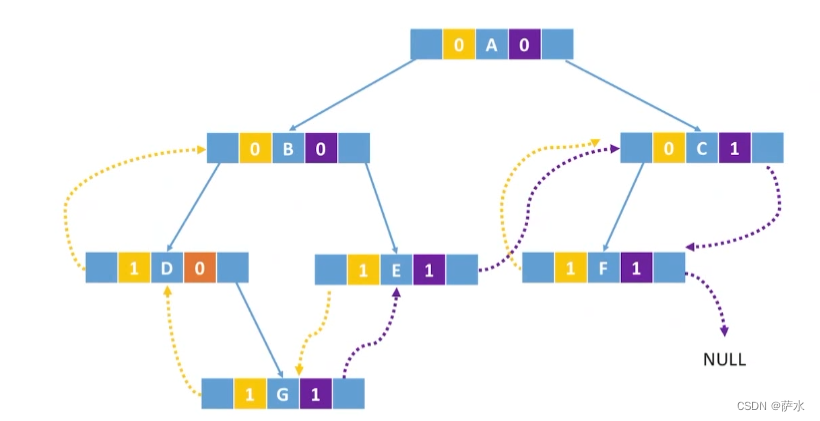
2、存储结构
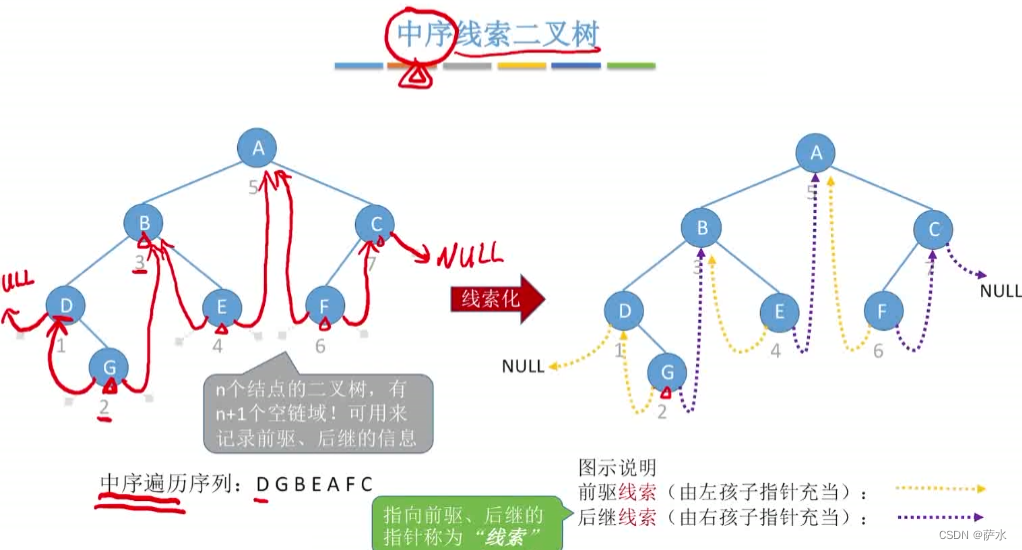
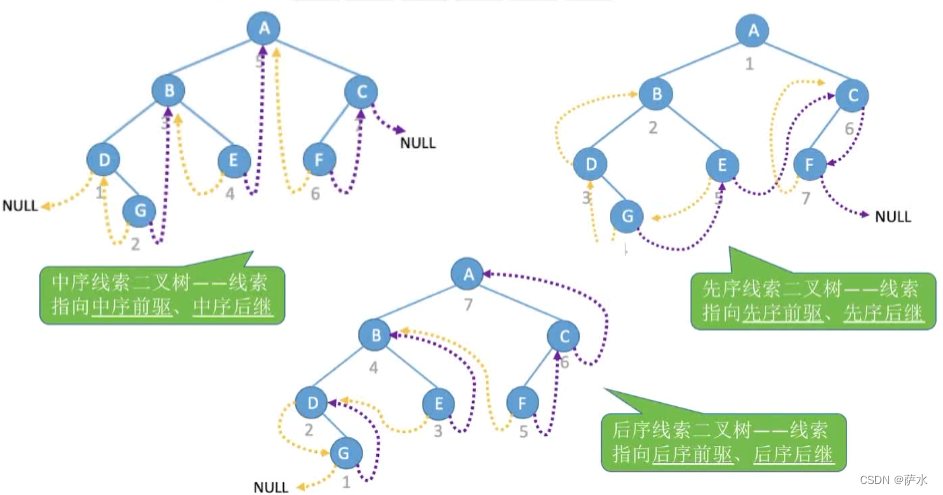
（1）中序线索二叉树
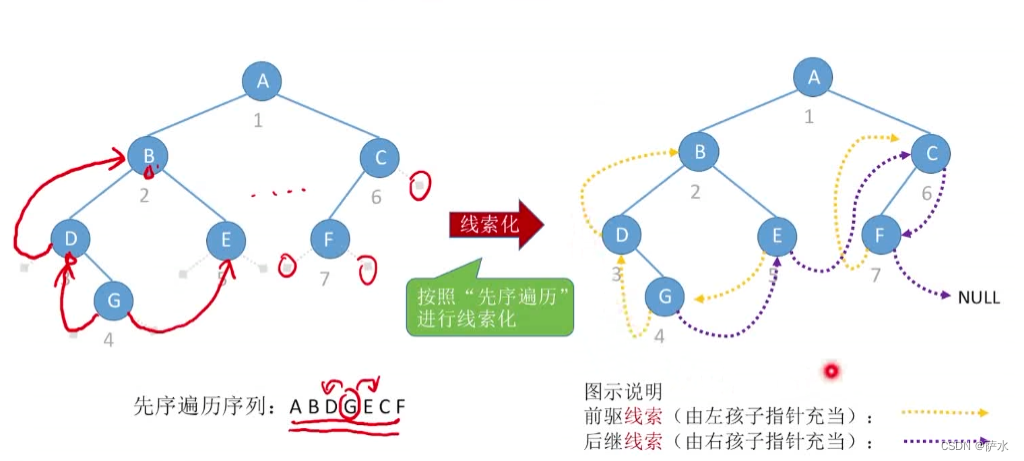
（2）先序线索二叉树
逻辑视角
存储视角
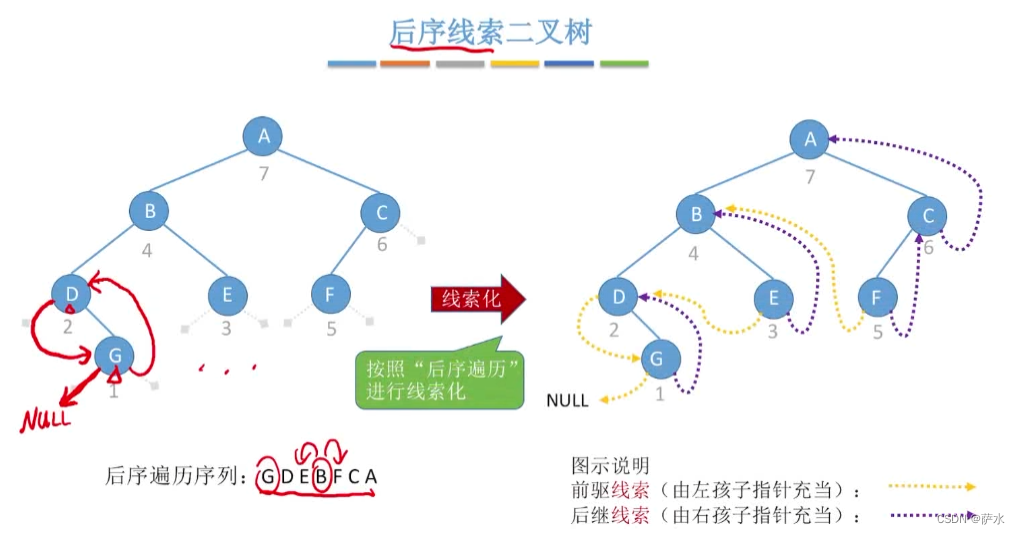
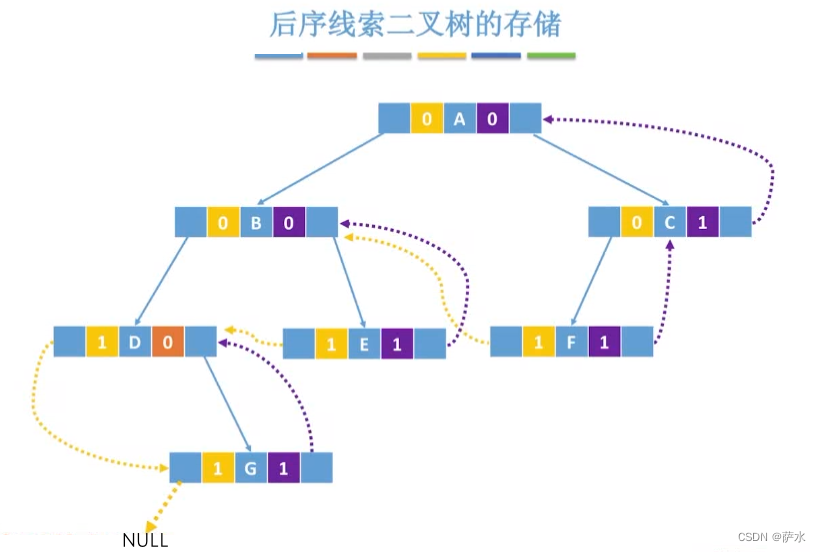
（3）后序线索二叉树
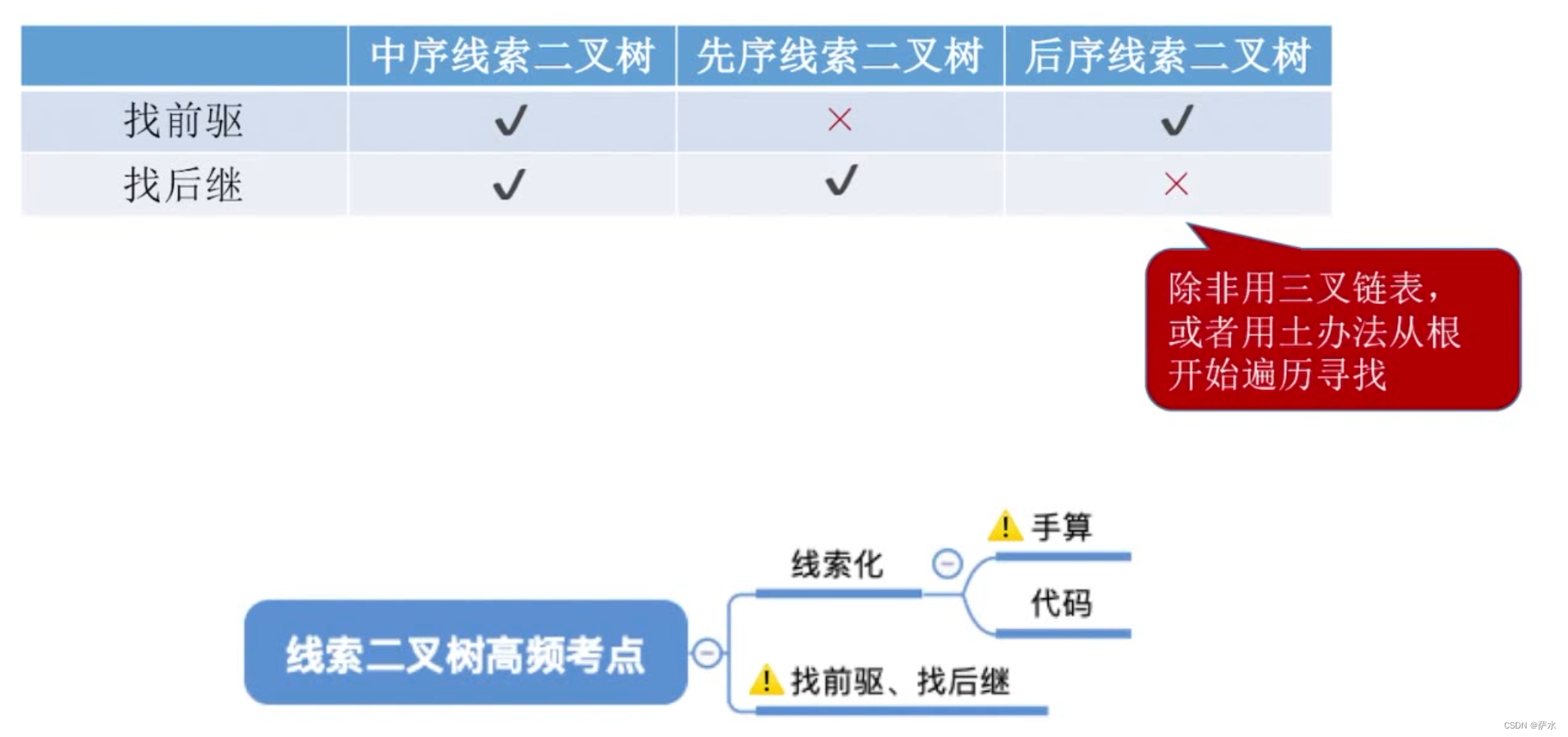
3、三种比较
4、小结
十、二叉树的线索化
知识总览
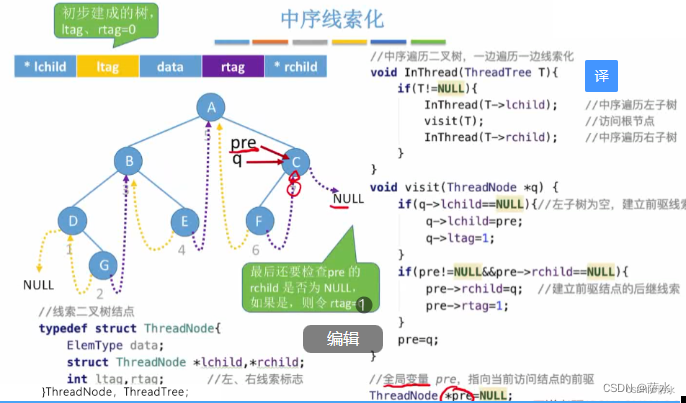
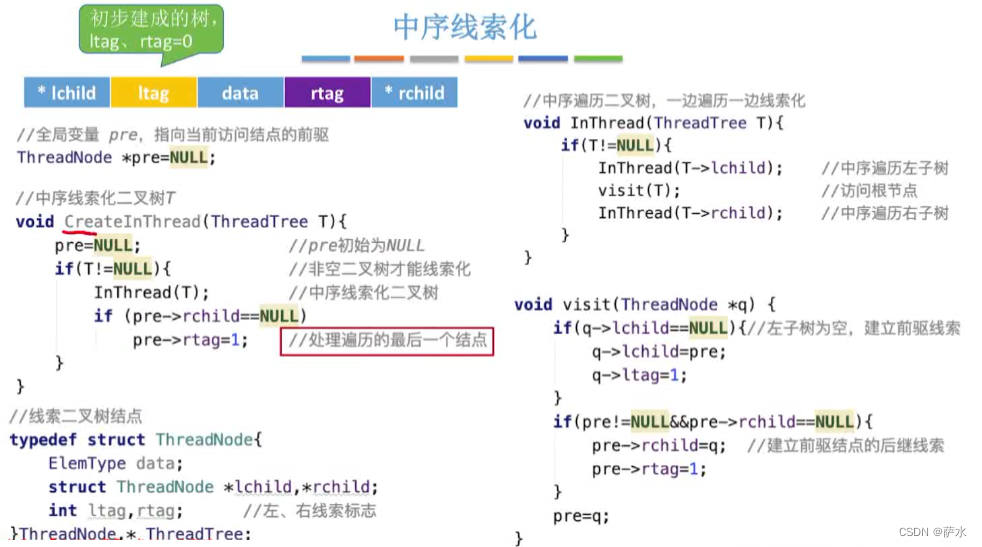
（1）中序线索化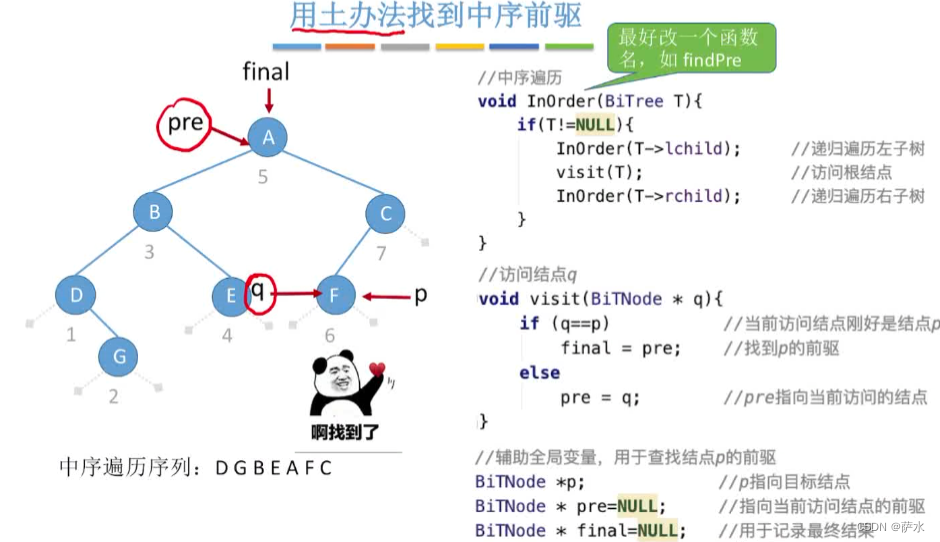
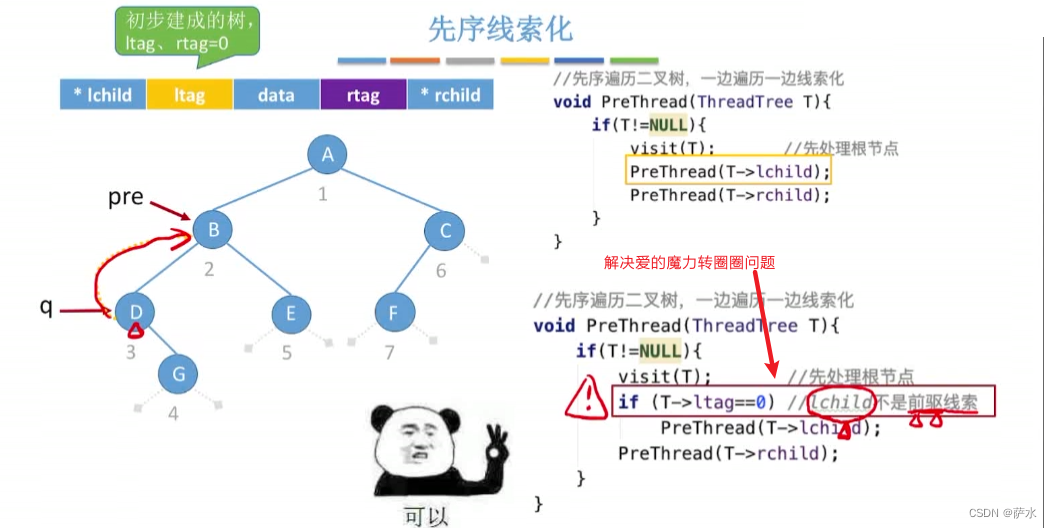
(2)先序线索化（存在转圈圈问题，注意解决方式）
（3）后序线索化
(4）小结
十一、线索二叉树--找前驱/后继
知识总览
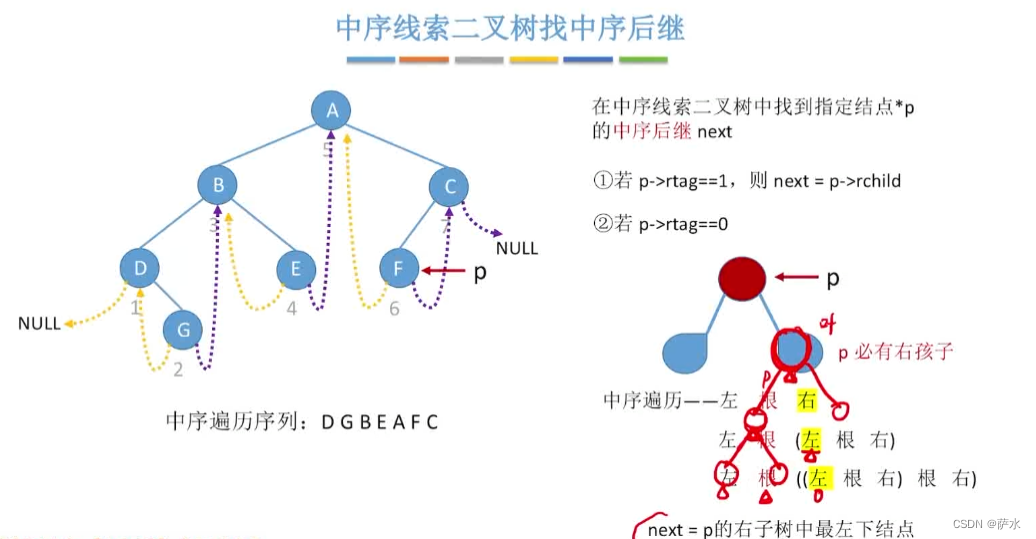
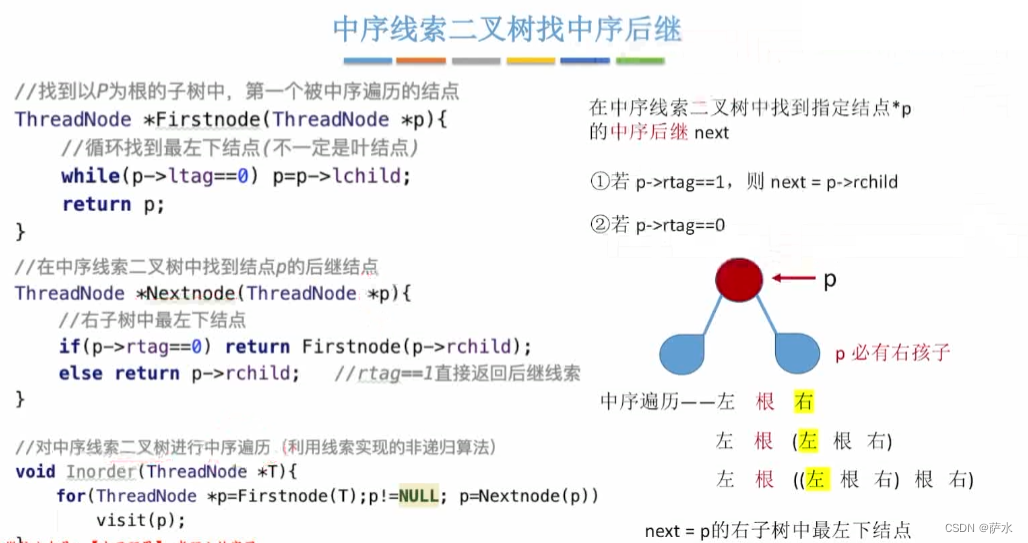
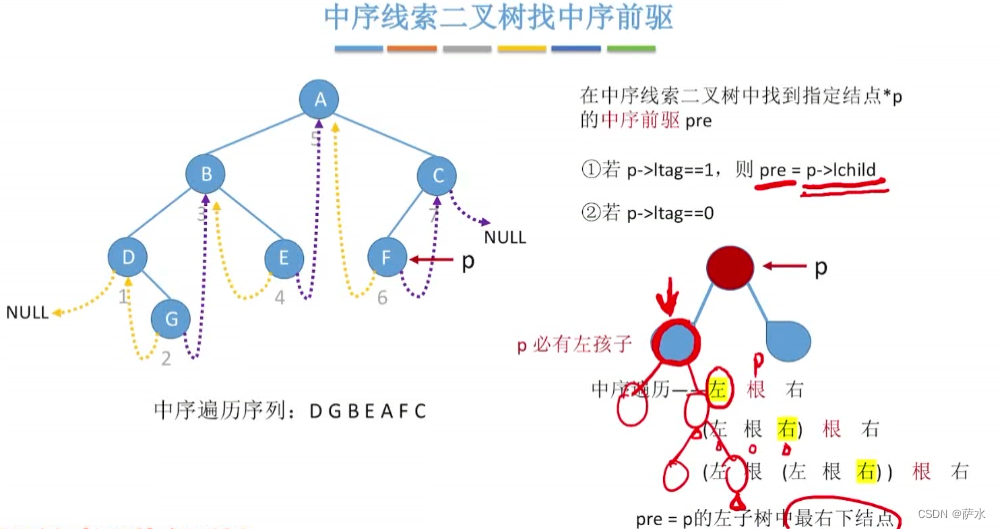
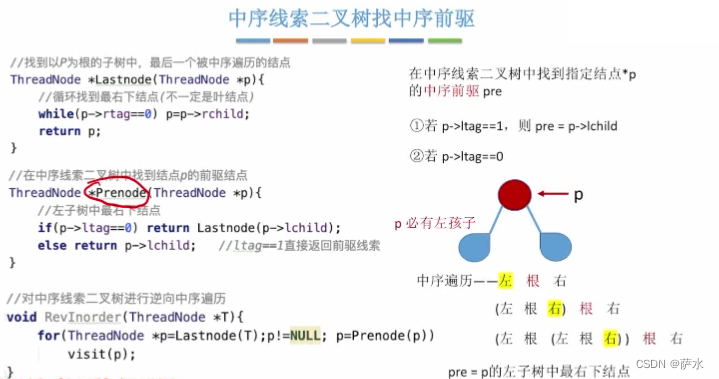
1、中序找后继/前驱
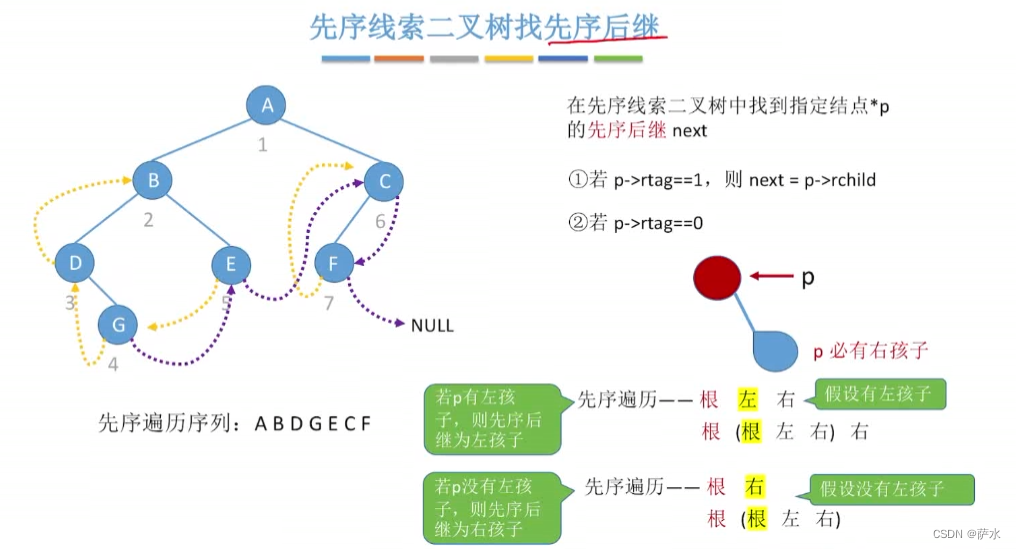
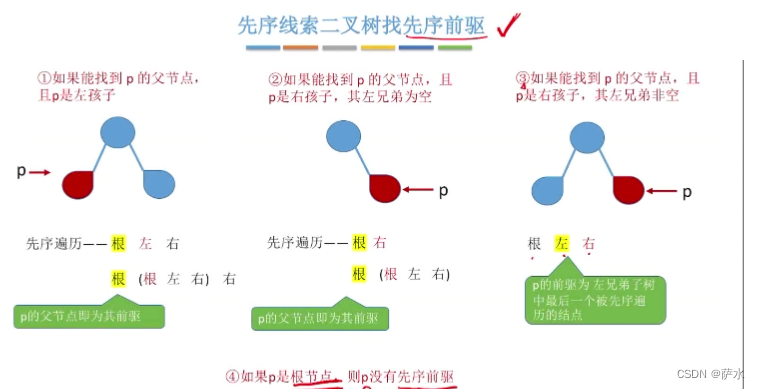
2、先序找后继/前驱
【注意】如果p是根节点，则 p 没有先序前驱
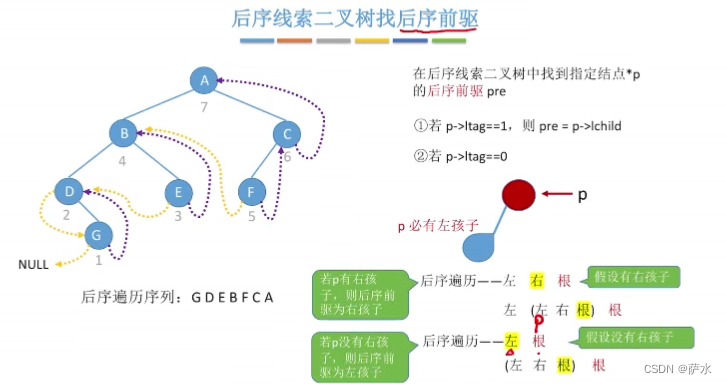
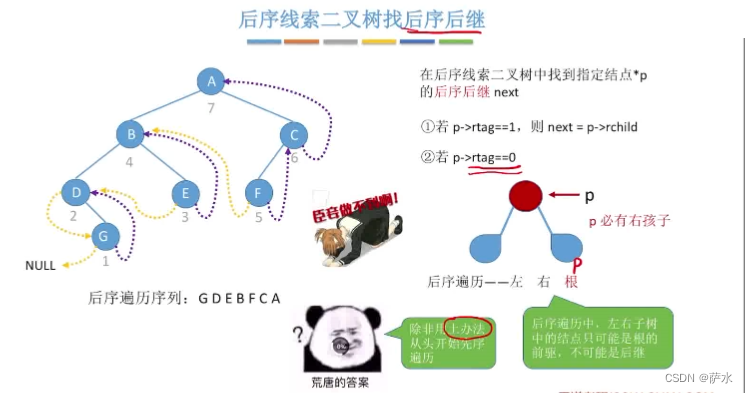
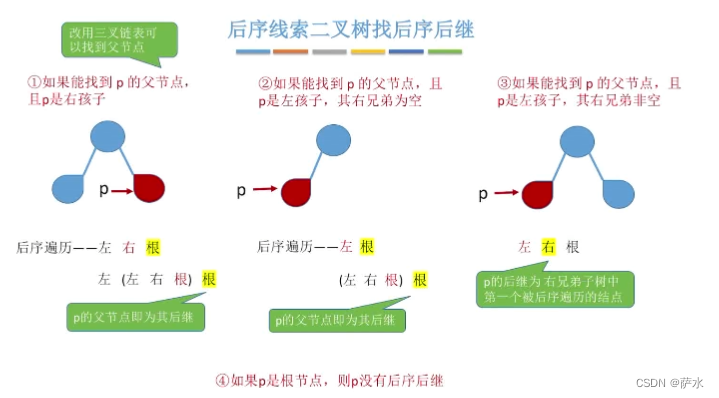
3、后序找后继/前驱
4、小结
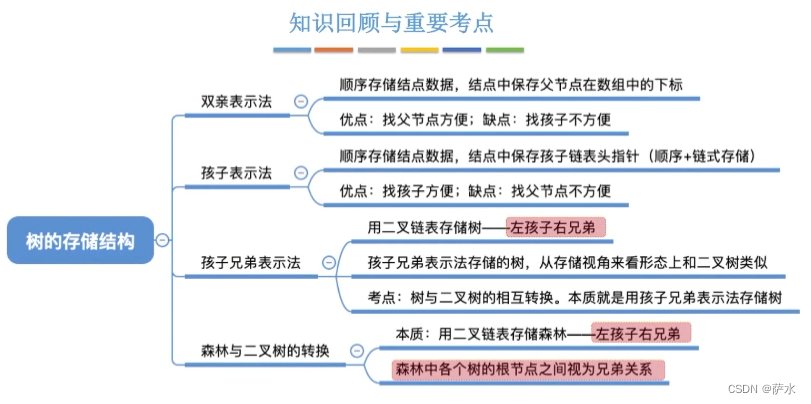
十二、树的存储结构
知识总览
1、树的逻辑结构
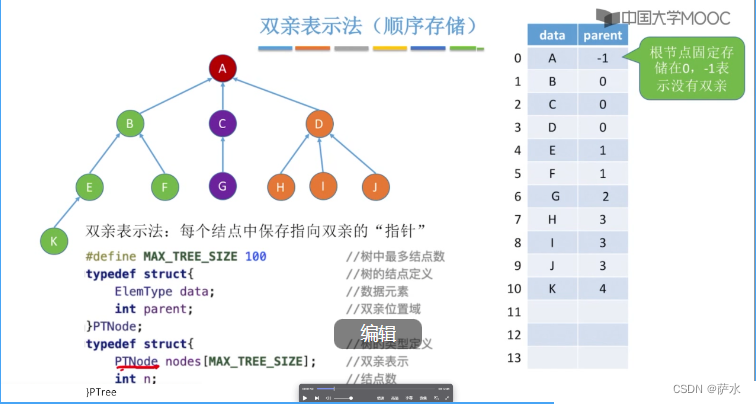
2、双亲表示法（顺序存储）
新增：先写值，然后写双亲结点数值
删除：
1、将值删除，双亲指向 -1
2、将最后的元素拿上来覆盖掉要删除的
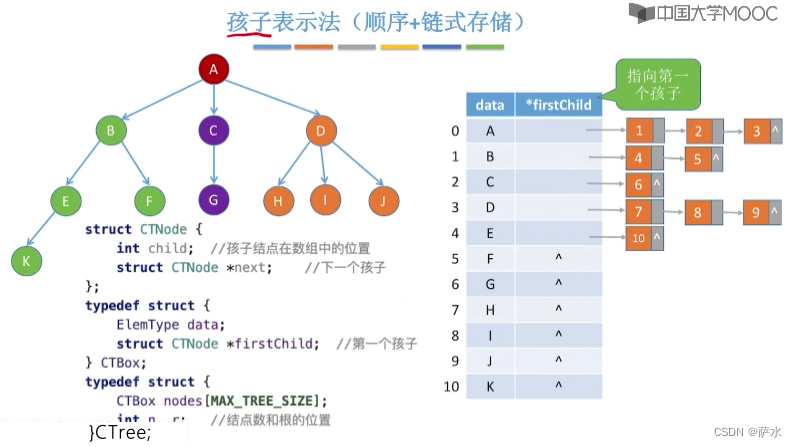
3、孩子表示法（顺序 + 链式存储）
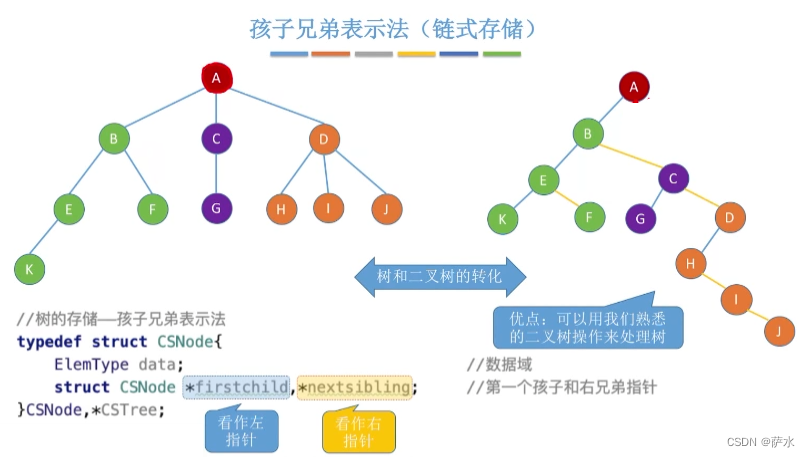
4、孩子兄弟表示法（链式存储）
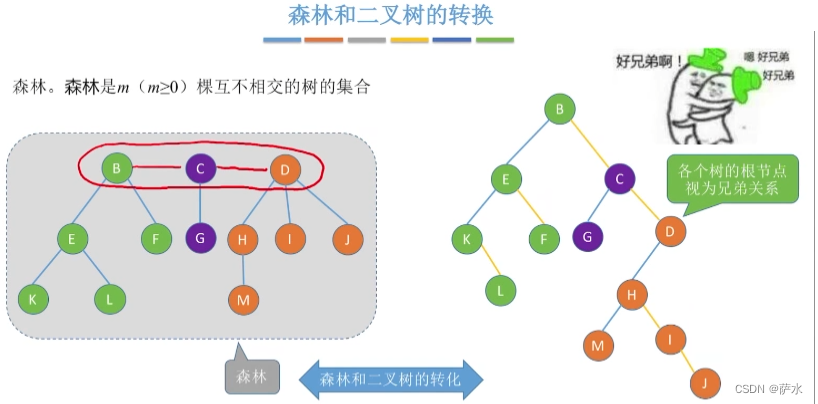
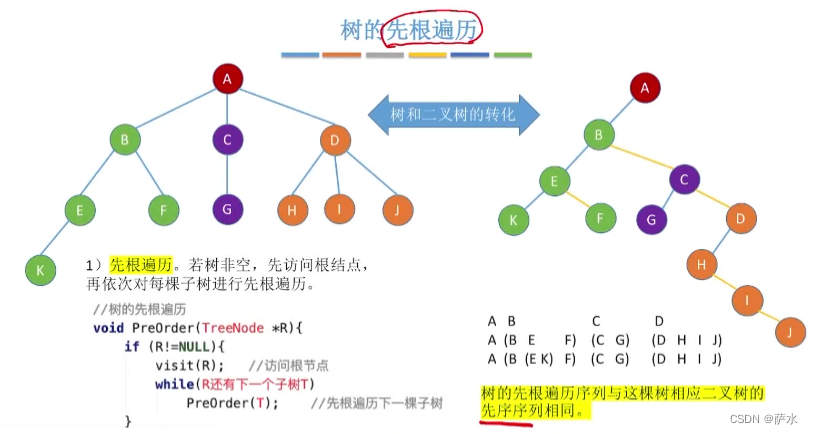
5、树和二叉树的转化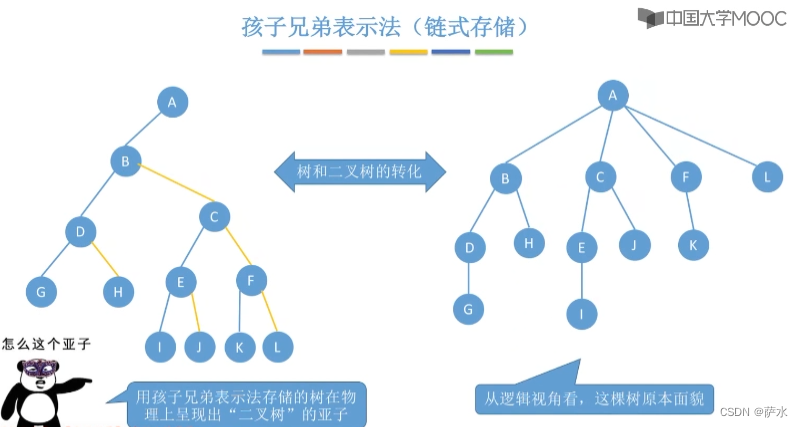
6、森林和二叉树的相互转换
7、小结
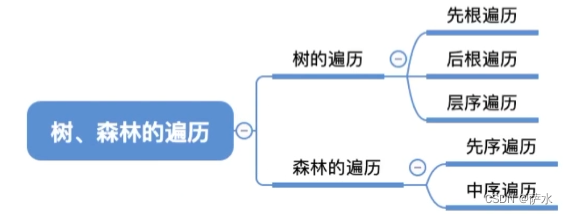
十三、树、森林的遍历
知识总览
1、树的遍历
（1）先根遍历（深度优先遍历）
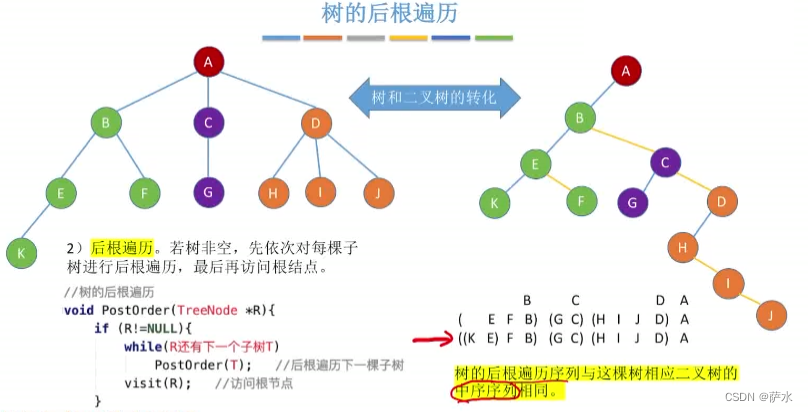
（2）后根遍历（深度优先遍历）
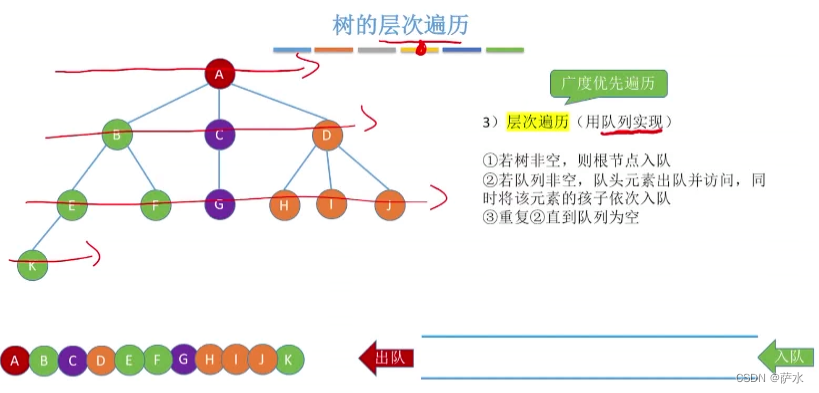
（3）树的层次遍历（广度优先遍历）
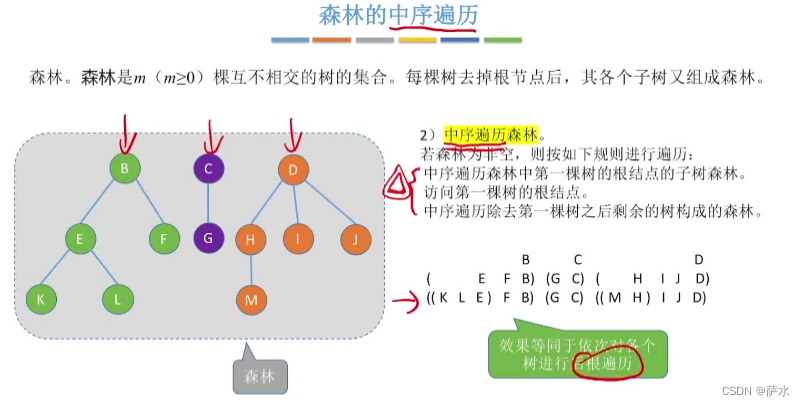
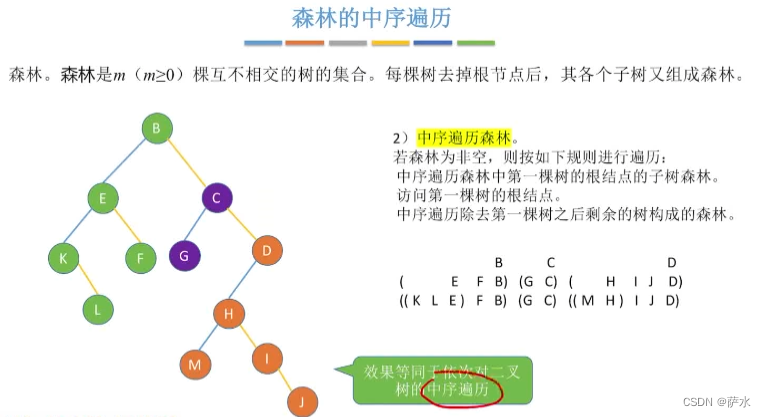
2、森林的遍历
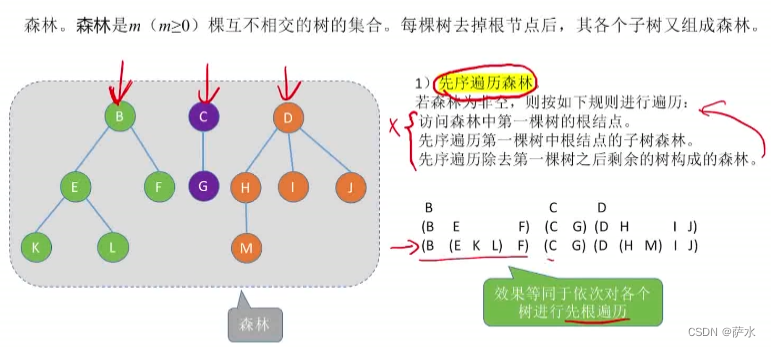
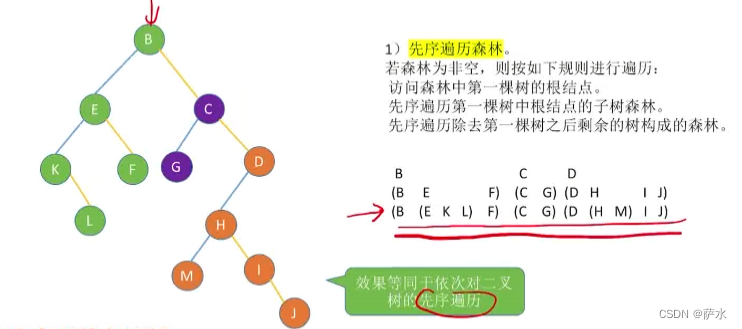
（1）先序遍历
方法一：效果等同于先根遍历
方法二：转为二叉树，效果上等同于先序遍历
（2）中序遍历
方法一：效果上等同于后根遍历
方法二：转为二叉树，效果上等同于中序遍历
3、小结
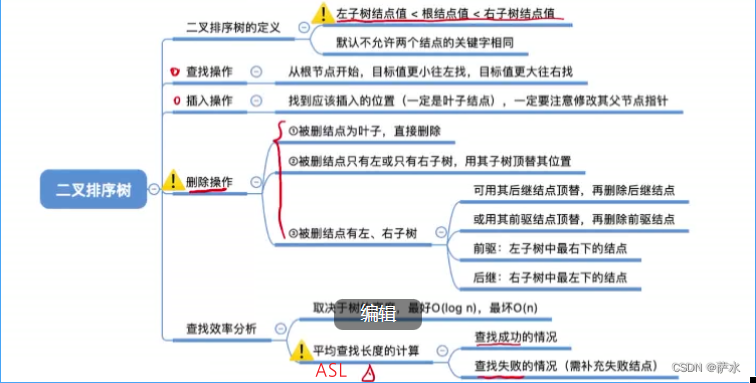
十四、二叉排序树（BST）
知识总览
1、二叉树定义
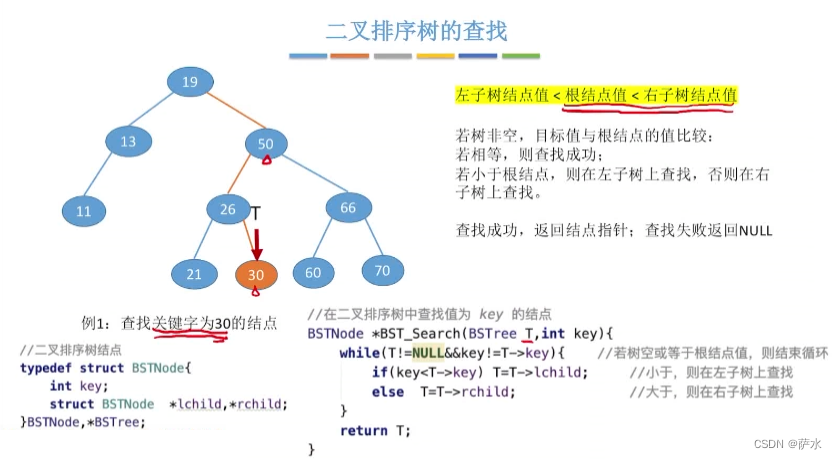
2、查找操作
递归实现
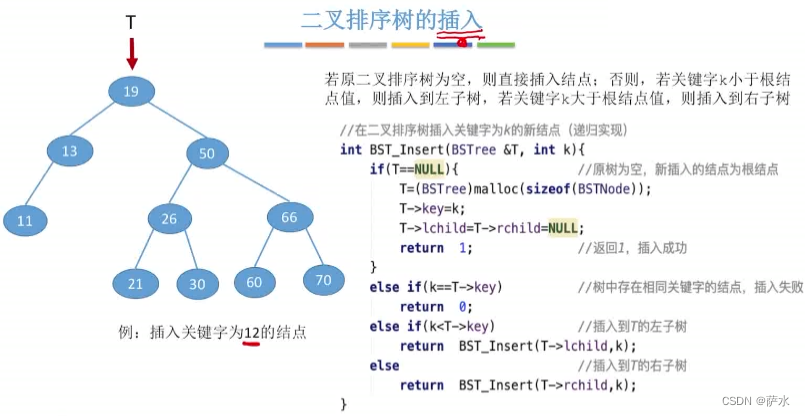
3、插入操作
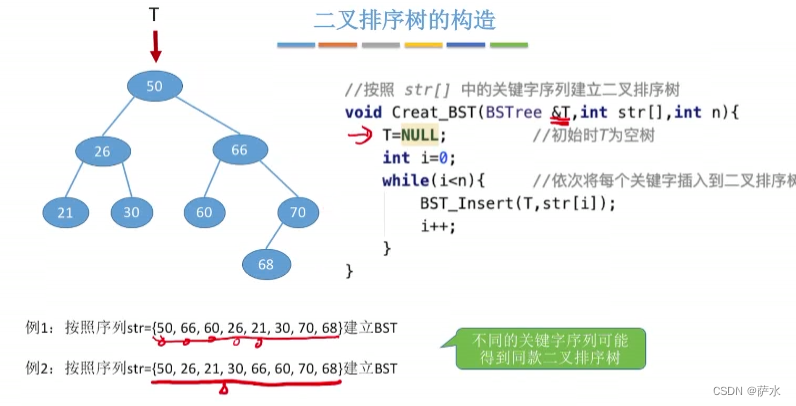
4、二叉排序树构造
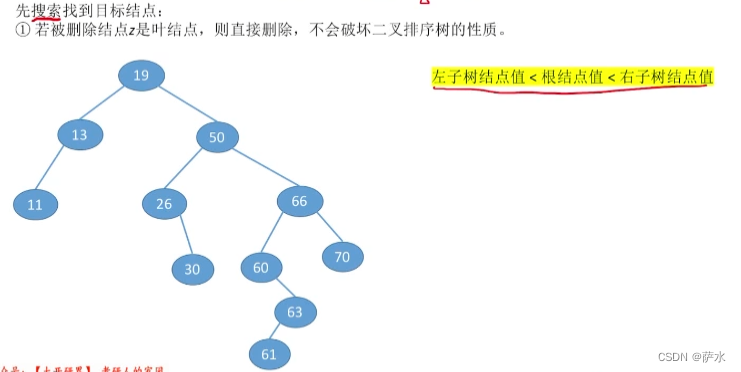
5、删除操作
（1）情况1：只删除叶子结点，直接删除，不会破坏
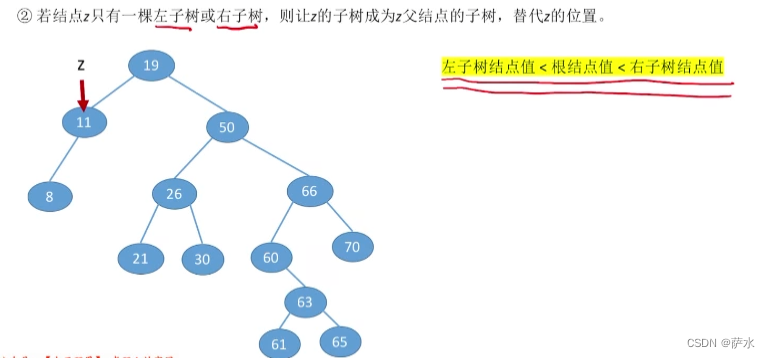
（2）情况2：只有左子树或右子树，则让z的子树成为z父节点的子树，替代z的位置
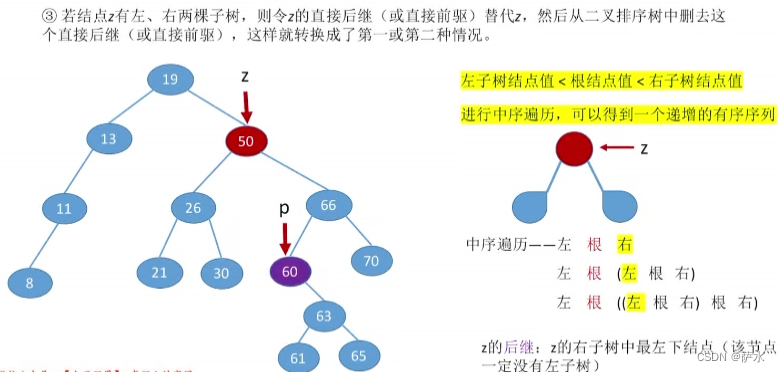
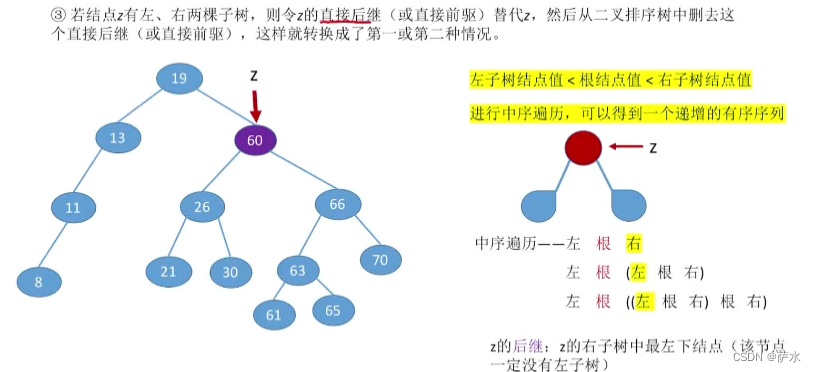
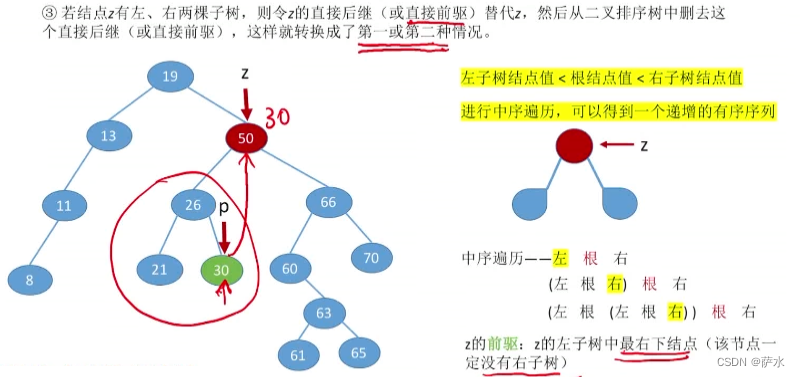
（3）情况3：
方式二：使用前驱替代
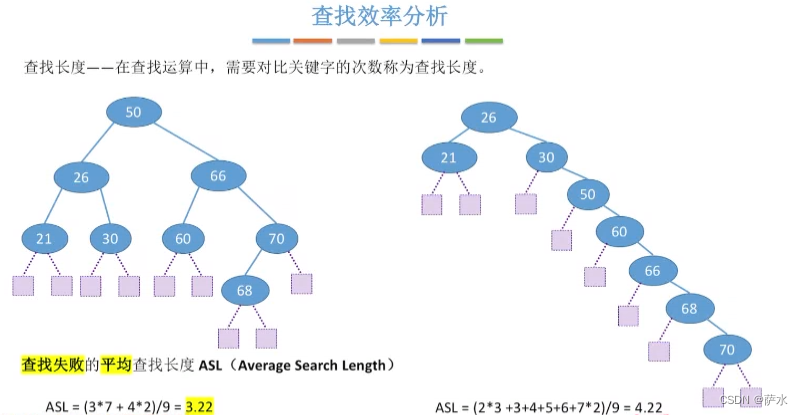
6、查找效率分析
查找长度概念：需要对比的关键字的次数
7、小结
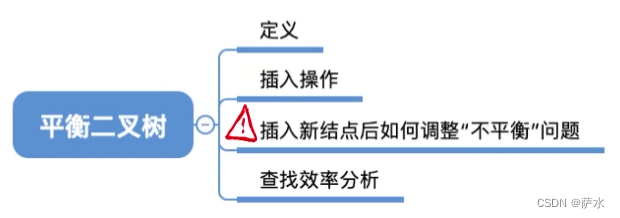
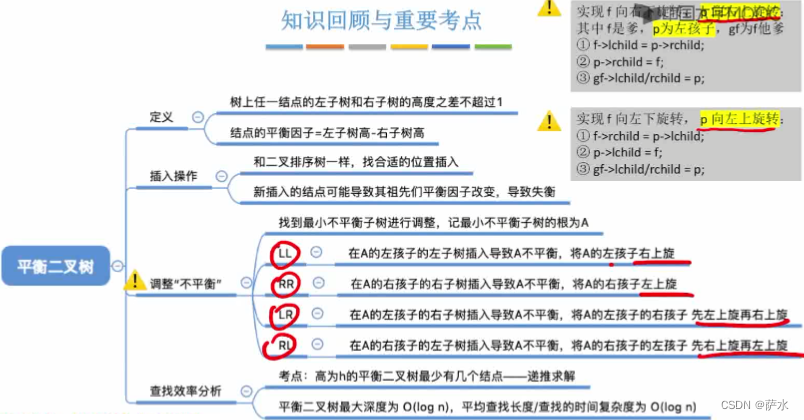
十五、平衡二叉树(AVL)
知识总览
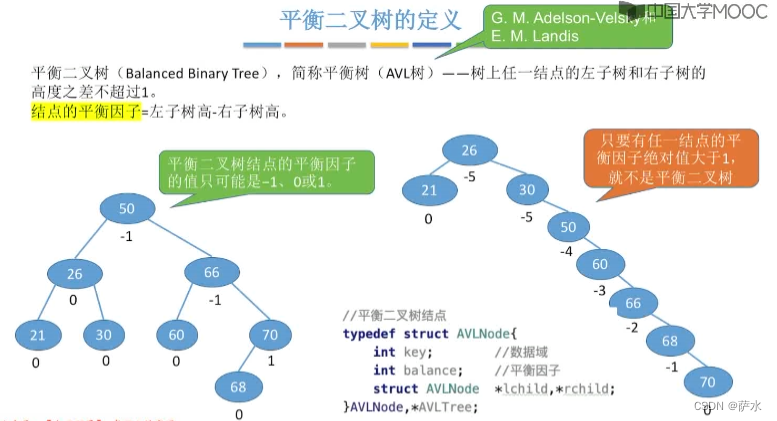
1、定义
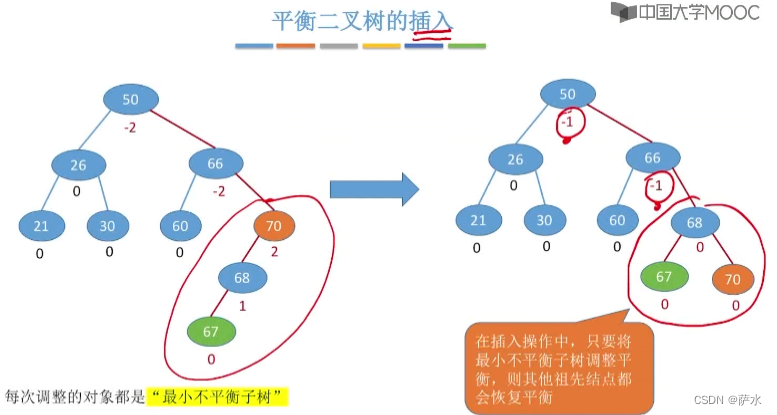
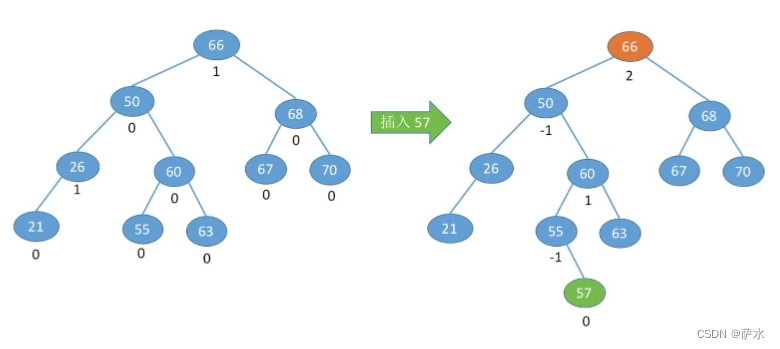
2、插入操作
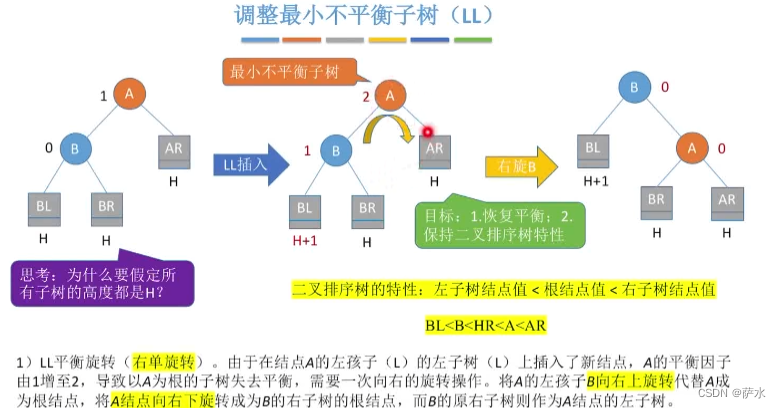
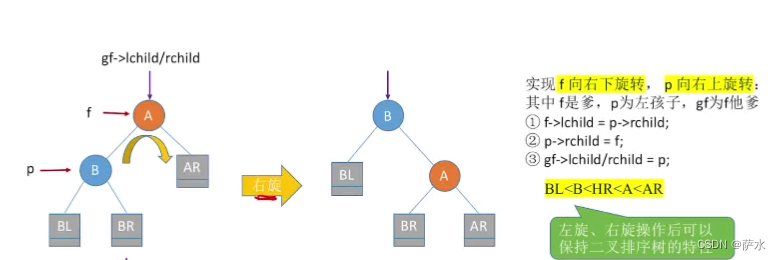
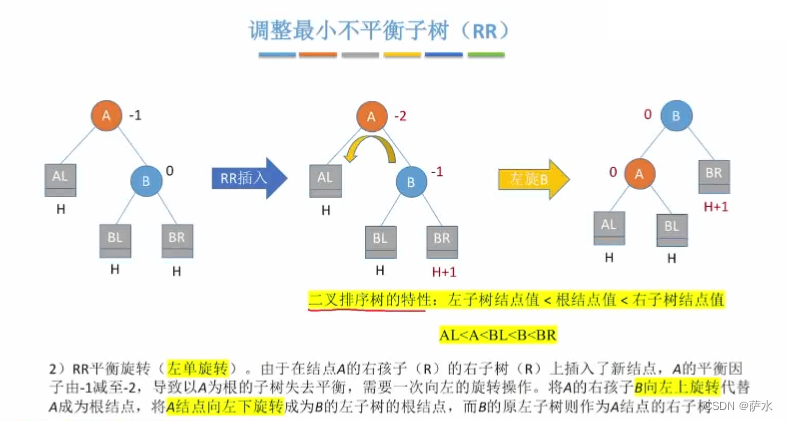
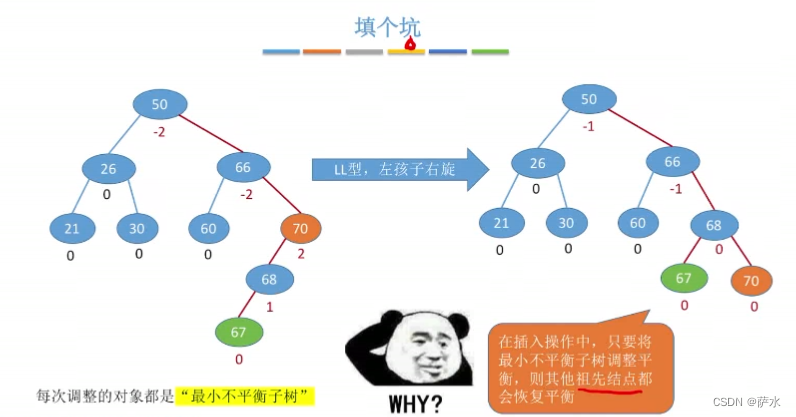
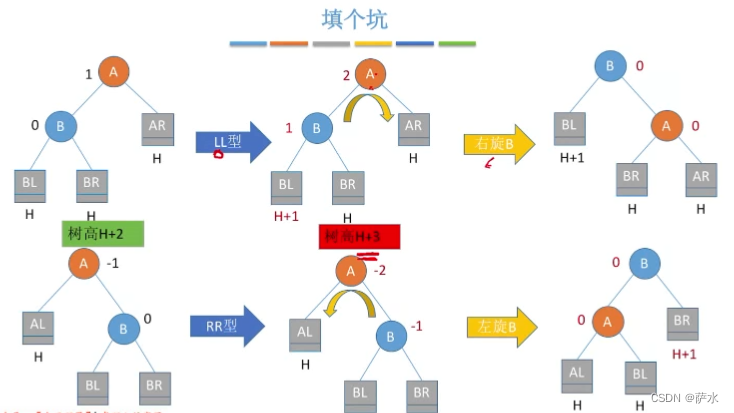
3、插入新结点后如何调整“不平衡”的问题
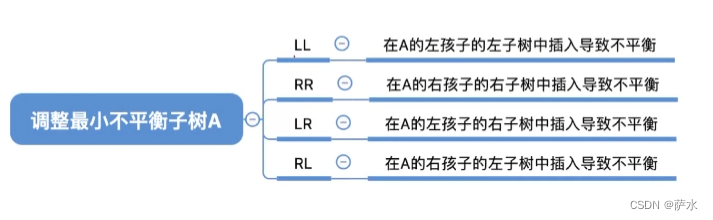
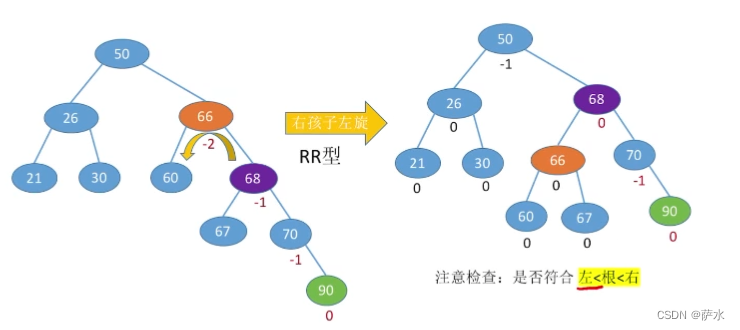
（2）RR
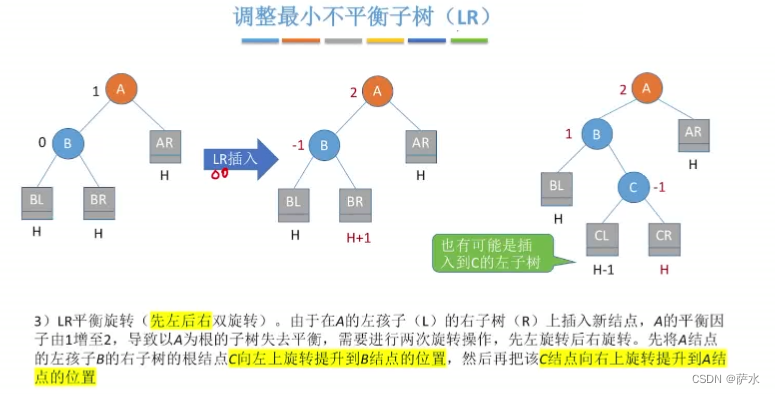
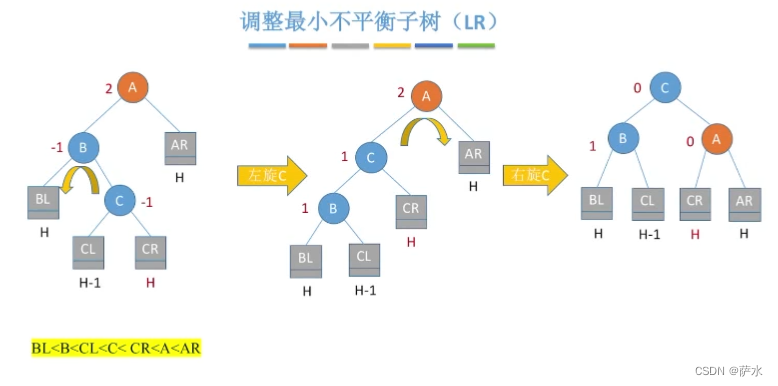
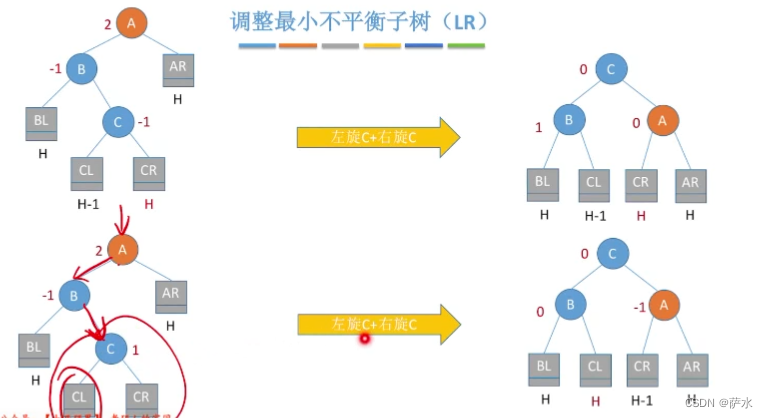
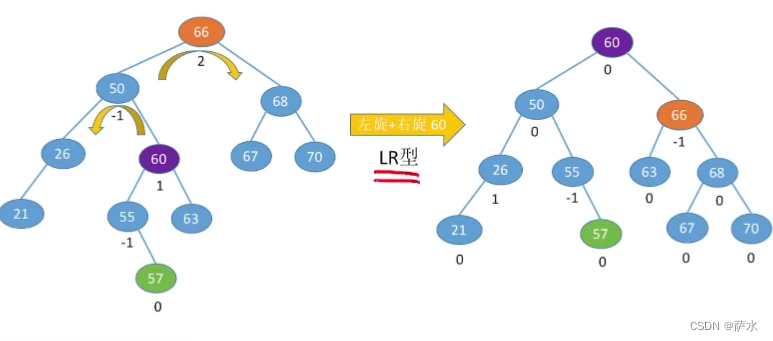
（3）LR
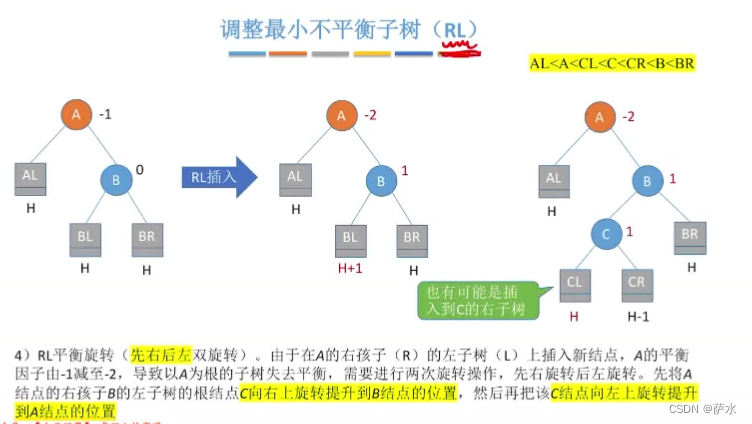
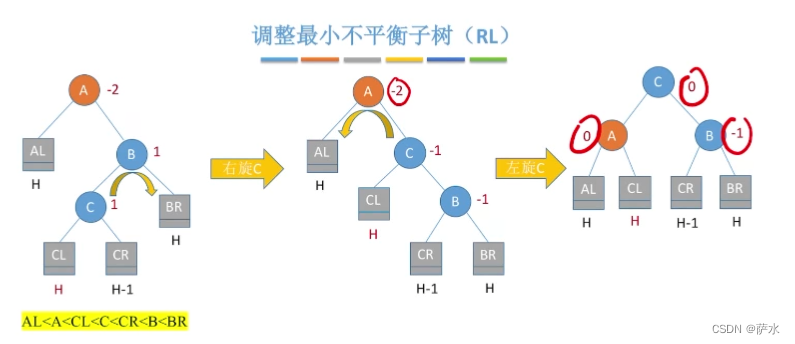
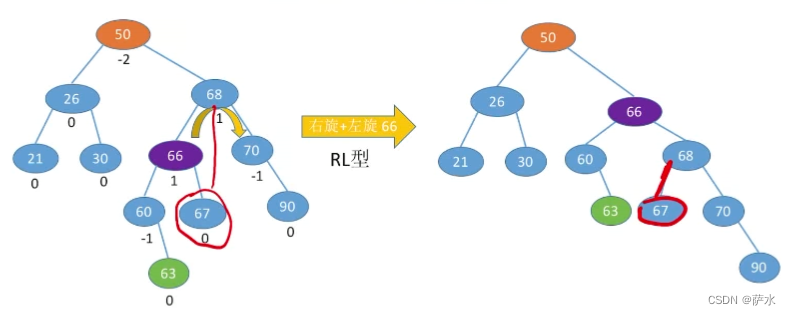
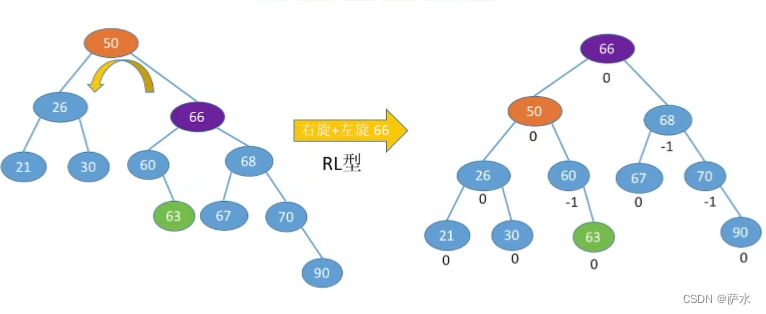
（4）RL
4、规律和比较
5、解答之前的一个疑问
5、练习
1、
2、
3、
6、查找效率分析
7、小结
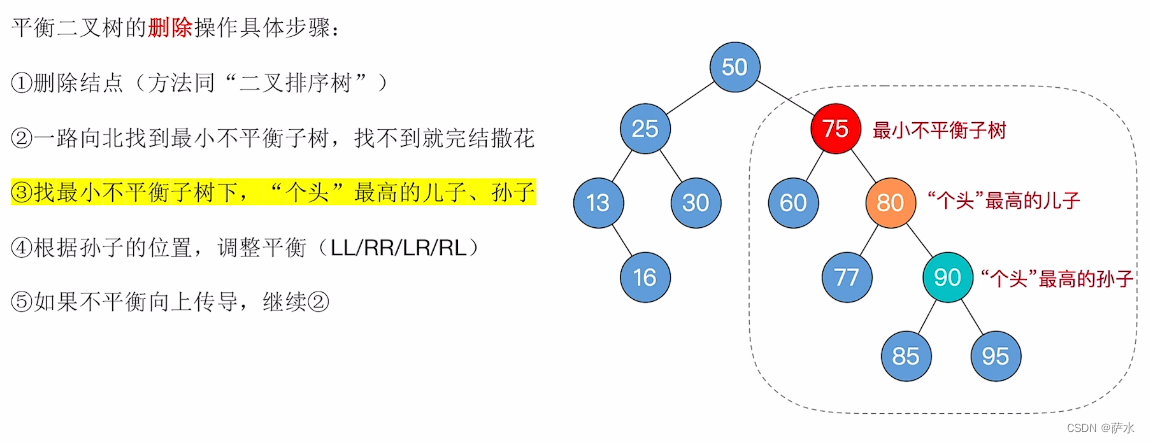
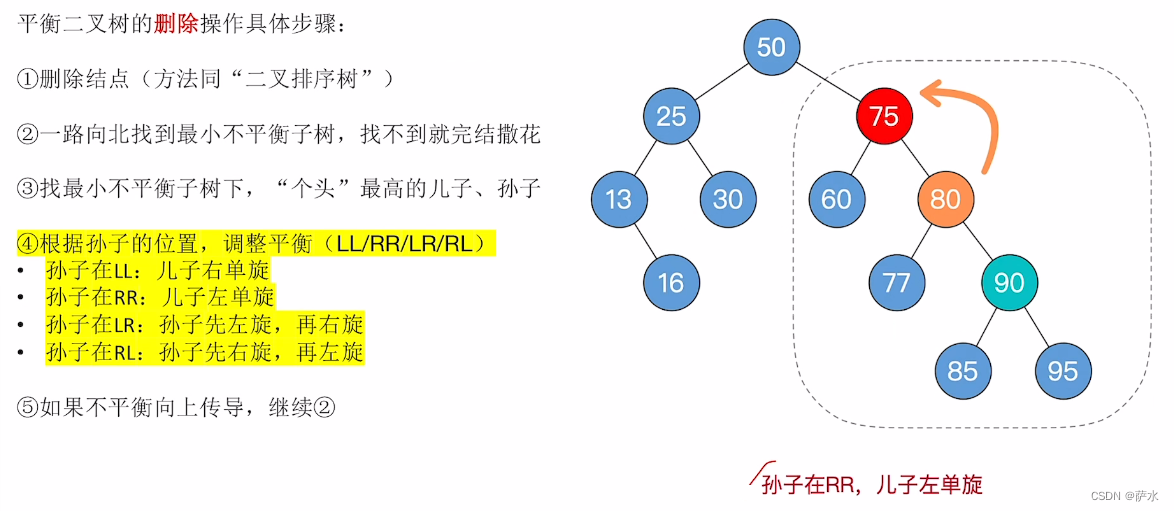
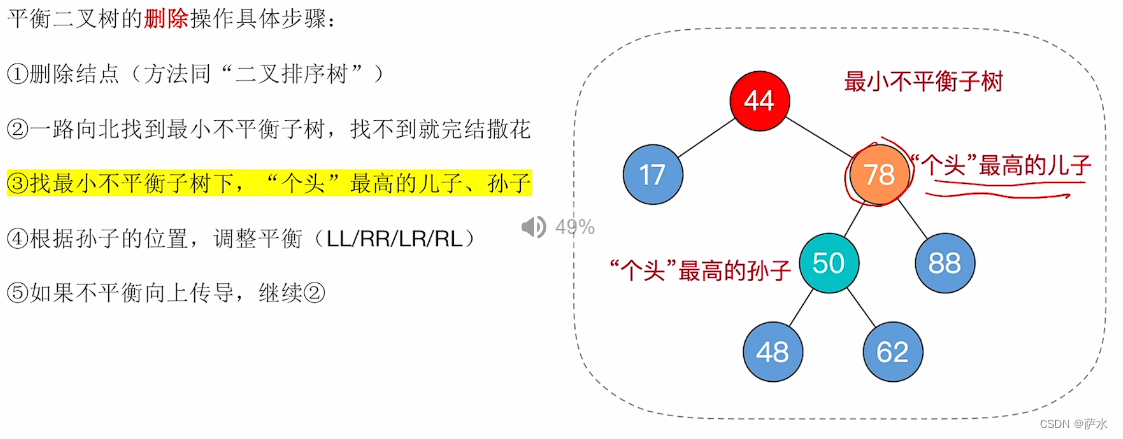
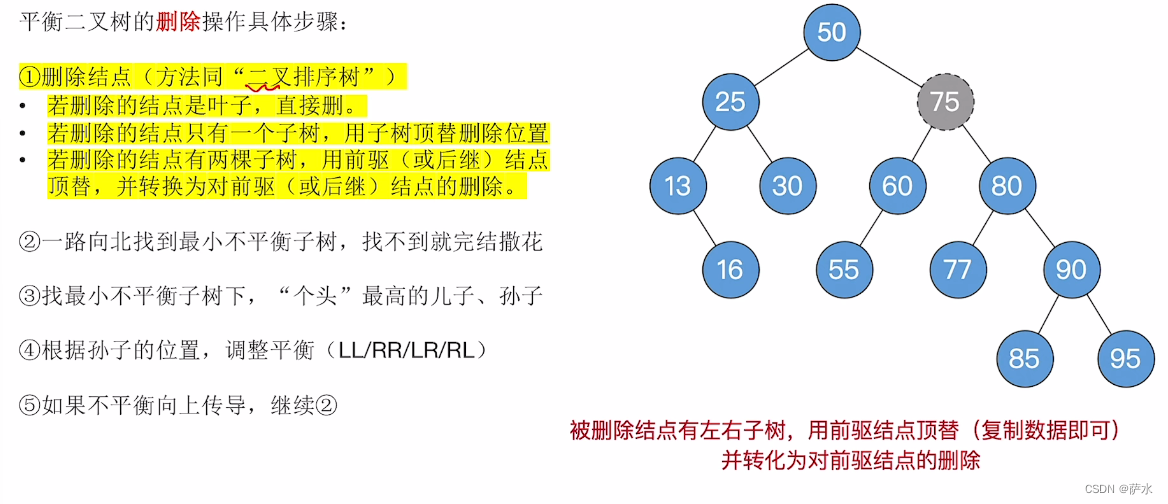
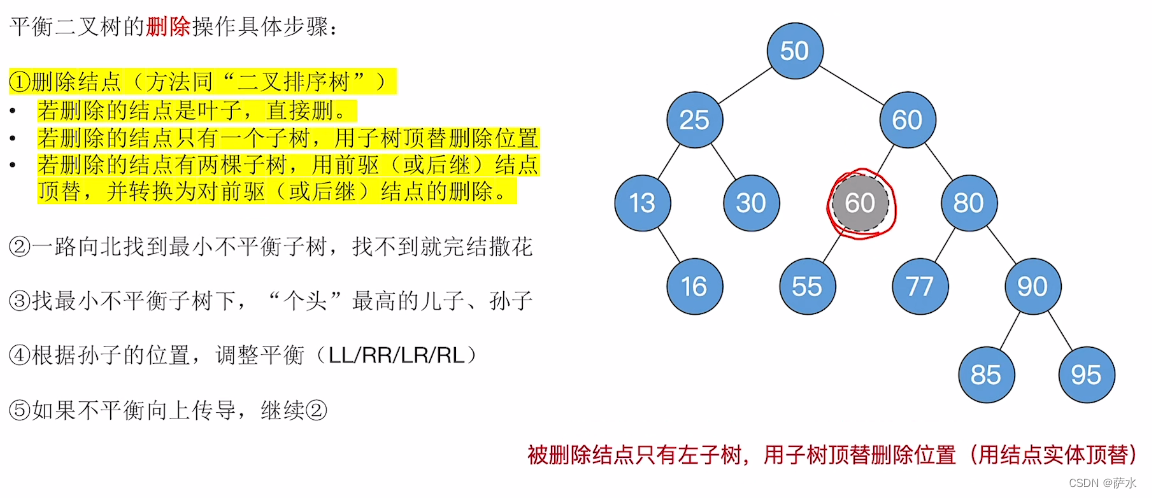
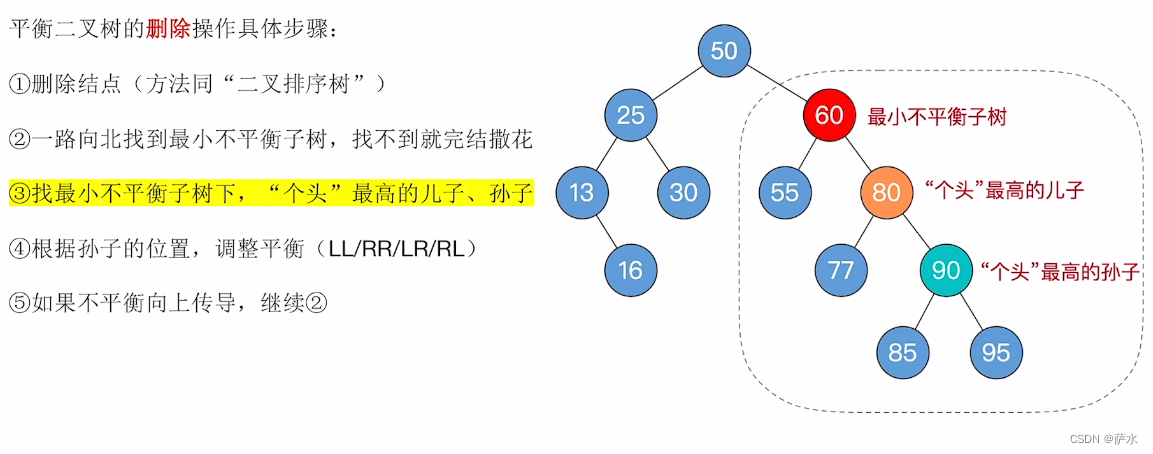
8、平衡二叉树的删除操作
例子
例一：
例二：
例3：
小结
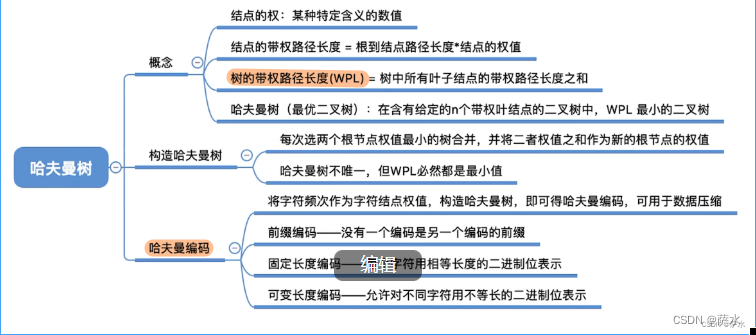
十六、Huffman（赫夫曼）树（最优二叉树）
知识总览
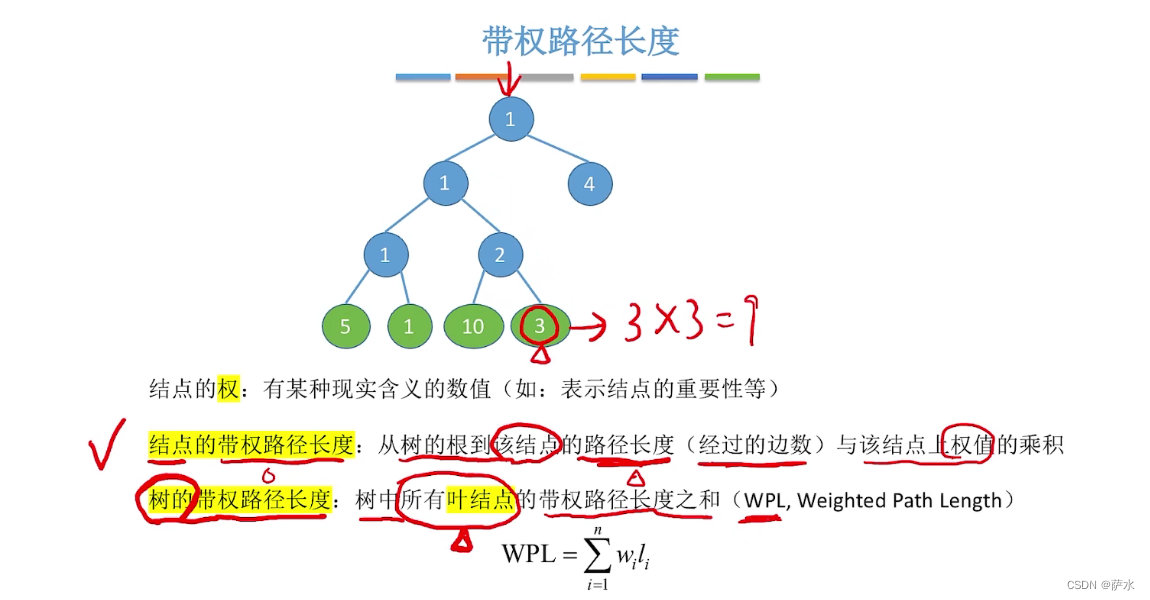
1、带权路径长度
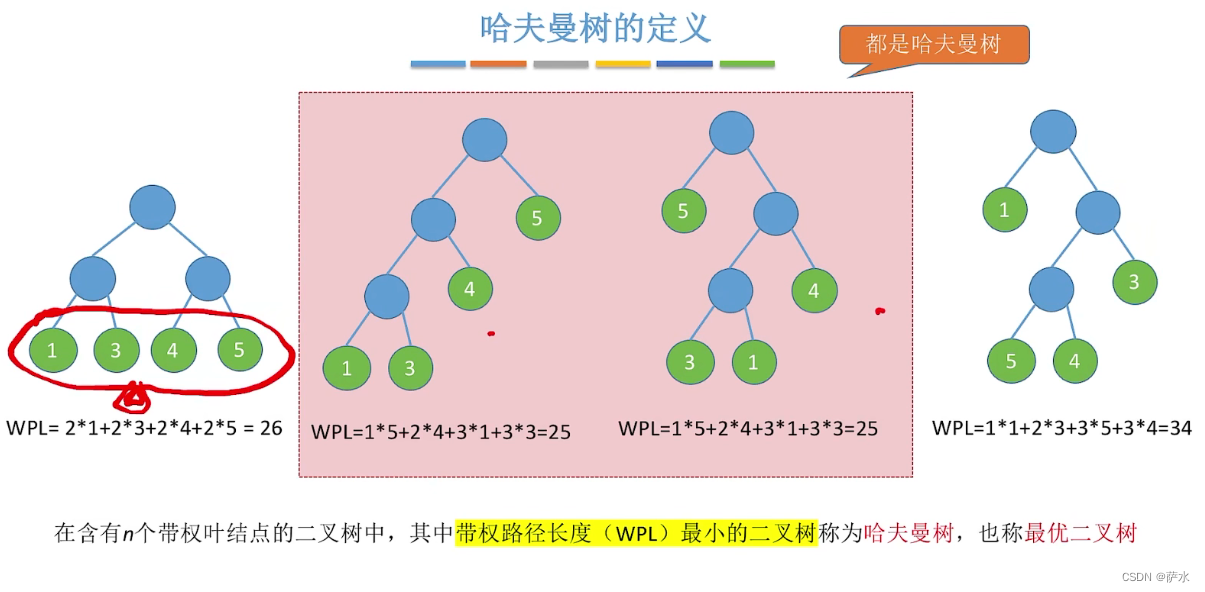
2、哈夫曼树的定义
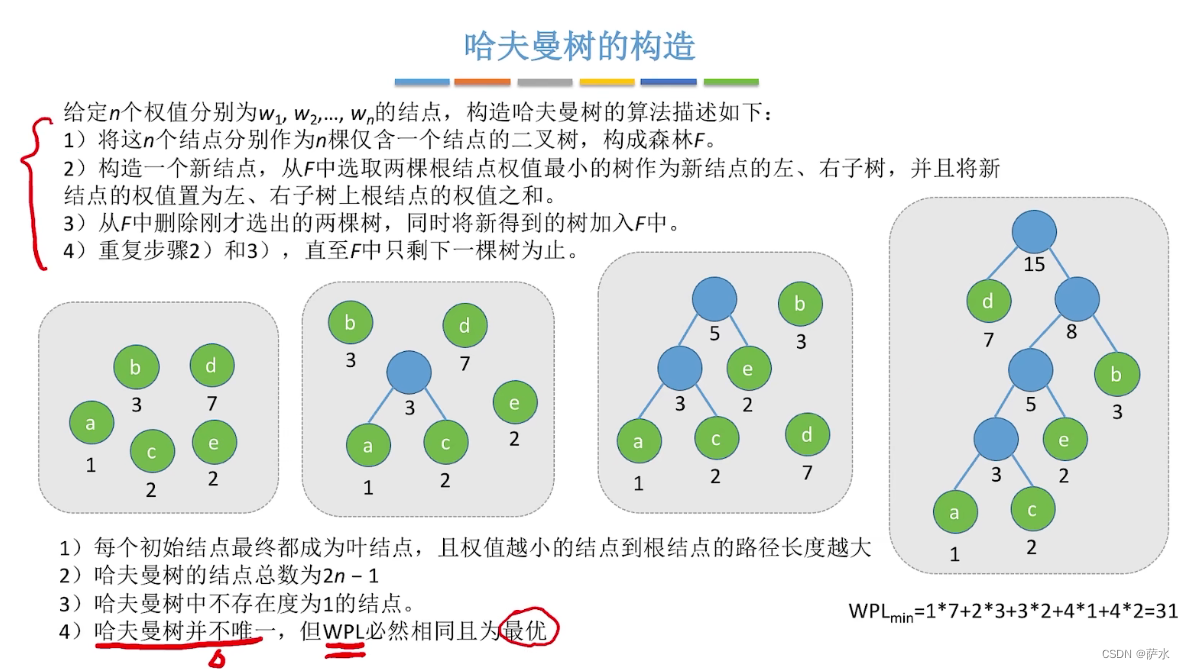
3、哈夫曼树的定义
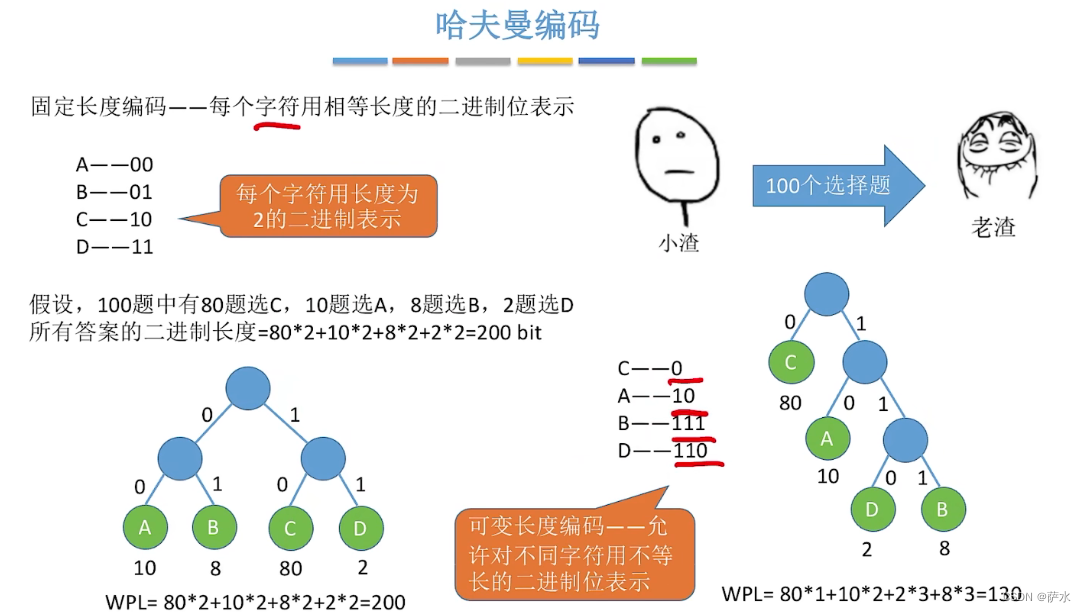
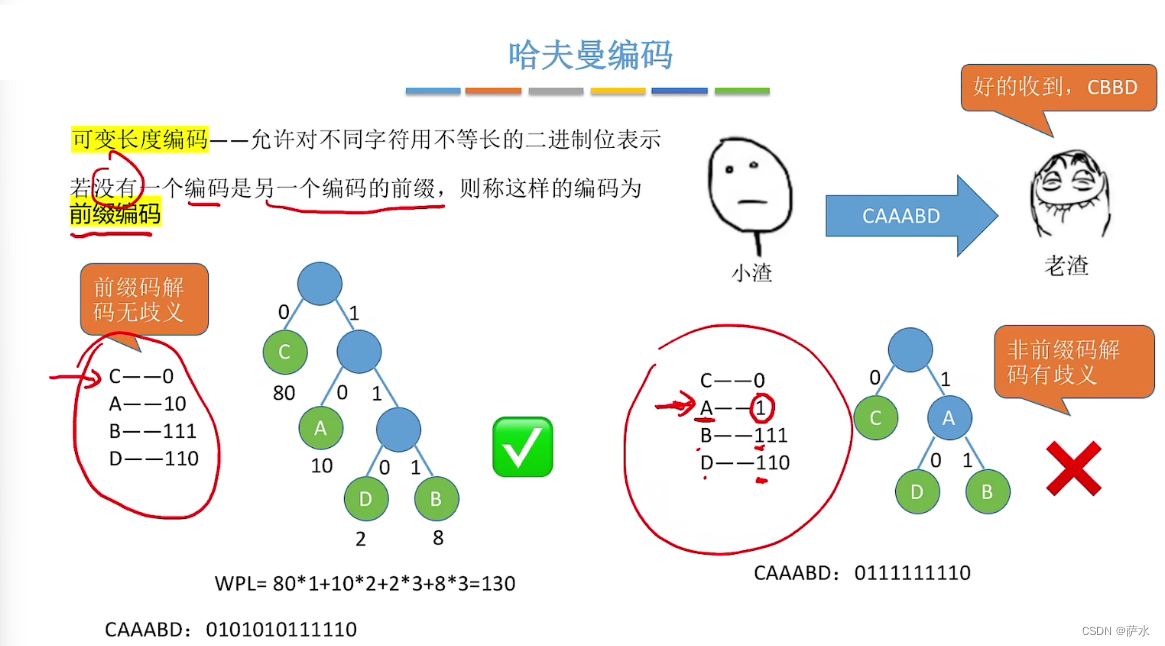
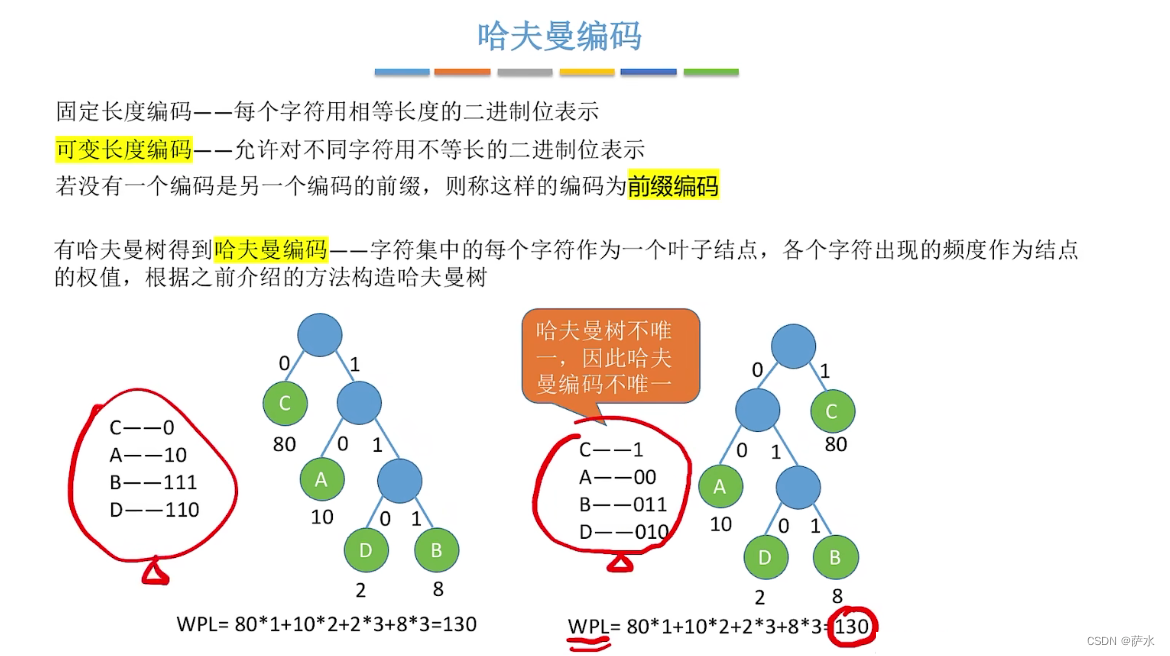
4、哈夫曼编码
【不能让编码的值作为结点，会出现错误】
5、小结
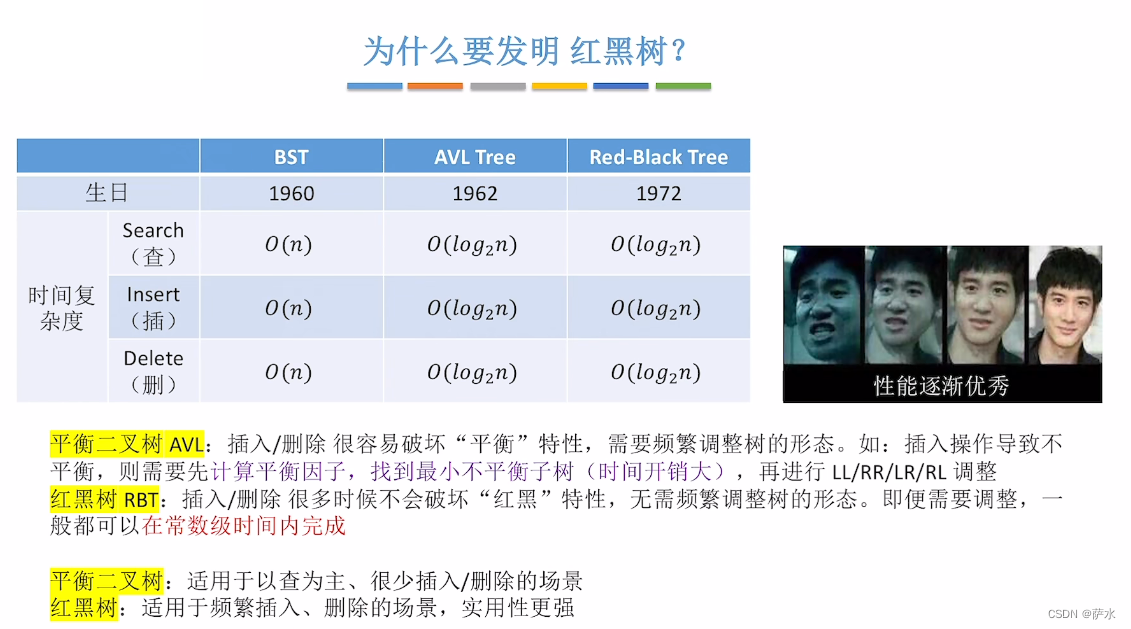
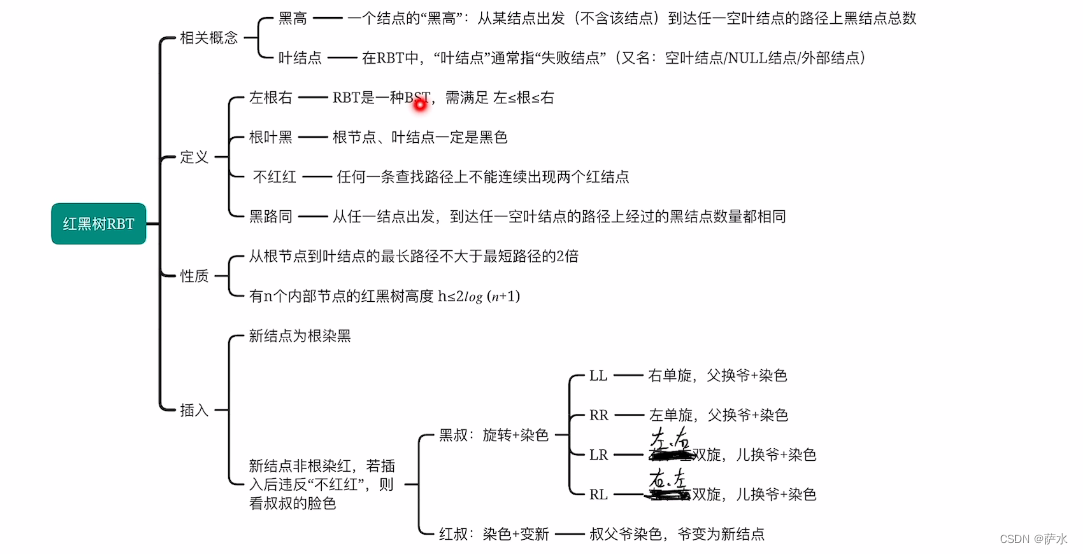
十七、红黑树（RBT）
为什么发明红黑树
红黑树大概怎么考
知识总览
1、红黑树的定义（二叉排序树的优化）
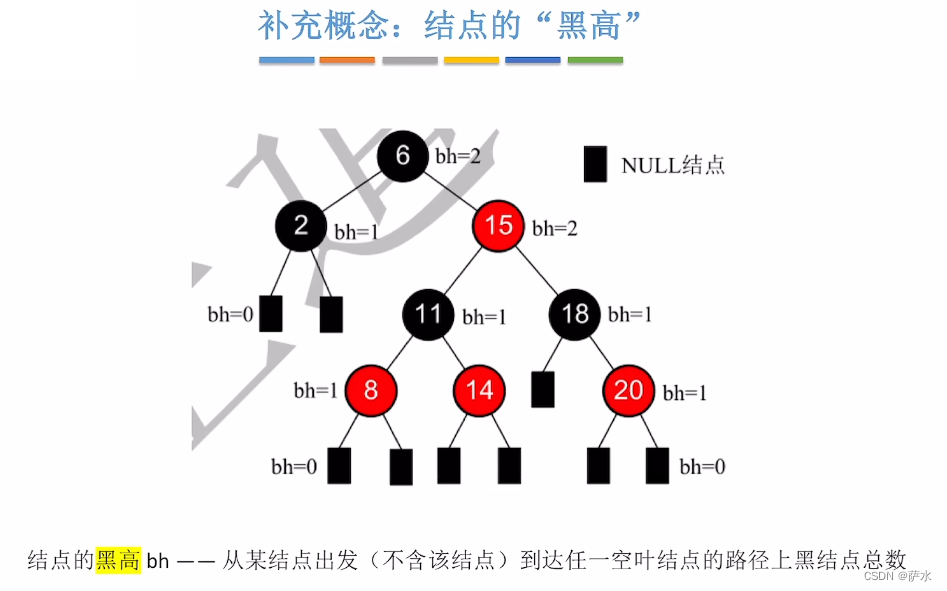
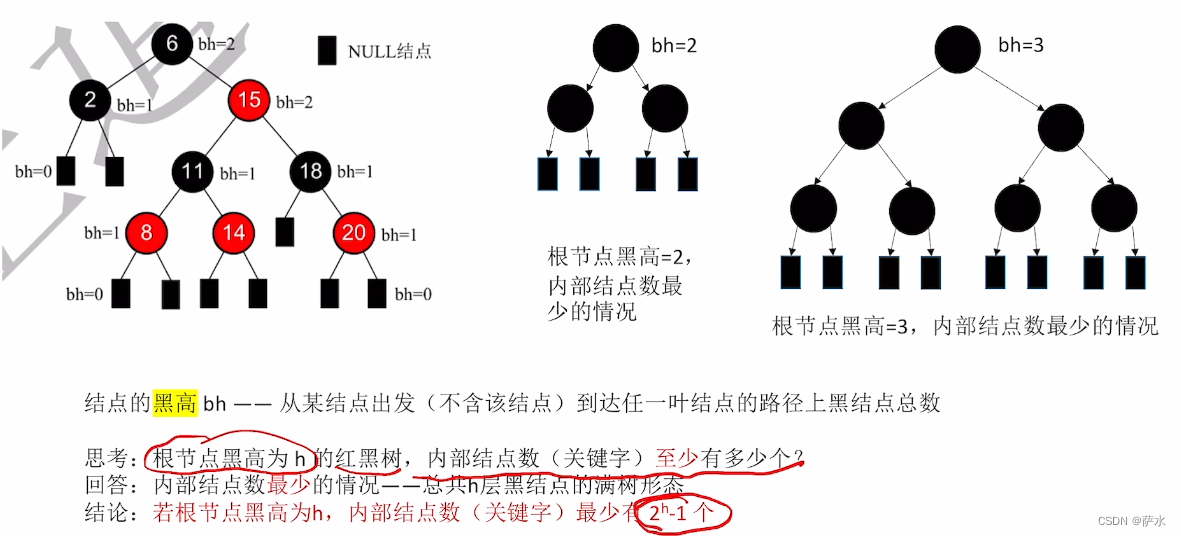
补充概念--黑高
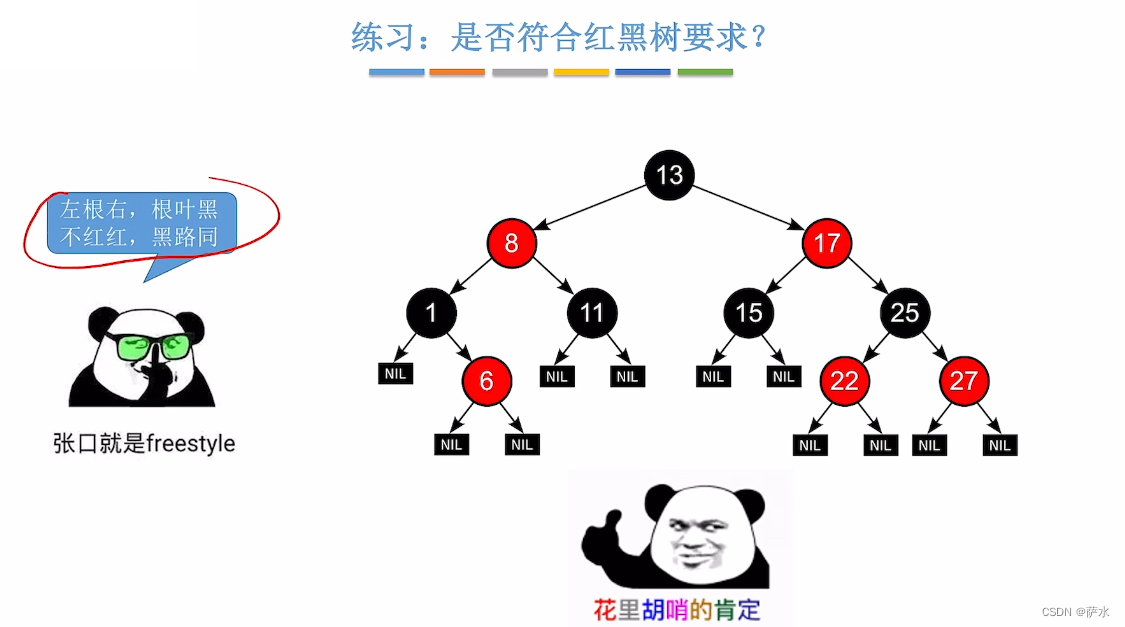
2、红黑树的性质
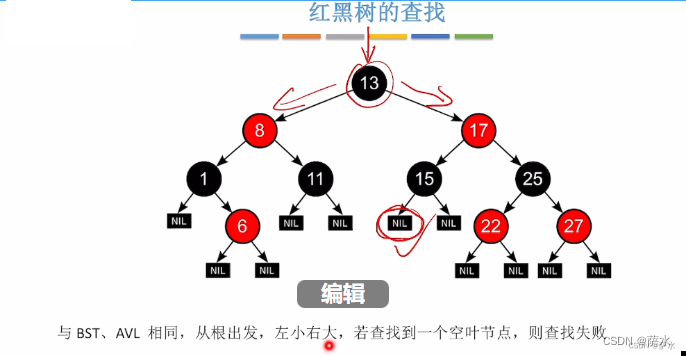
3、红黑树的查找
4、红黑树的插入
5、与“黑高”相关的推论
6、红黑树删除操作
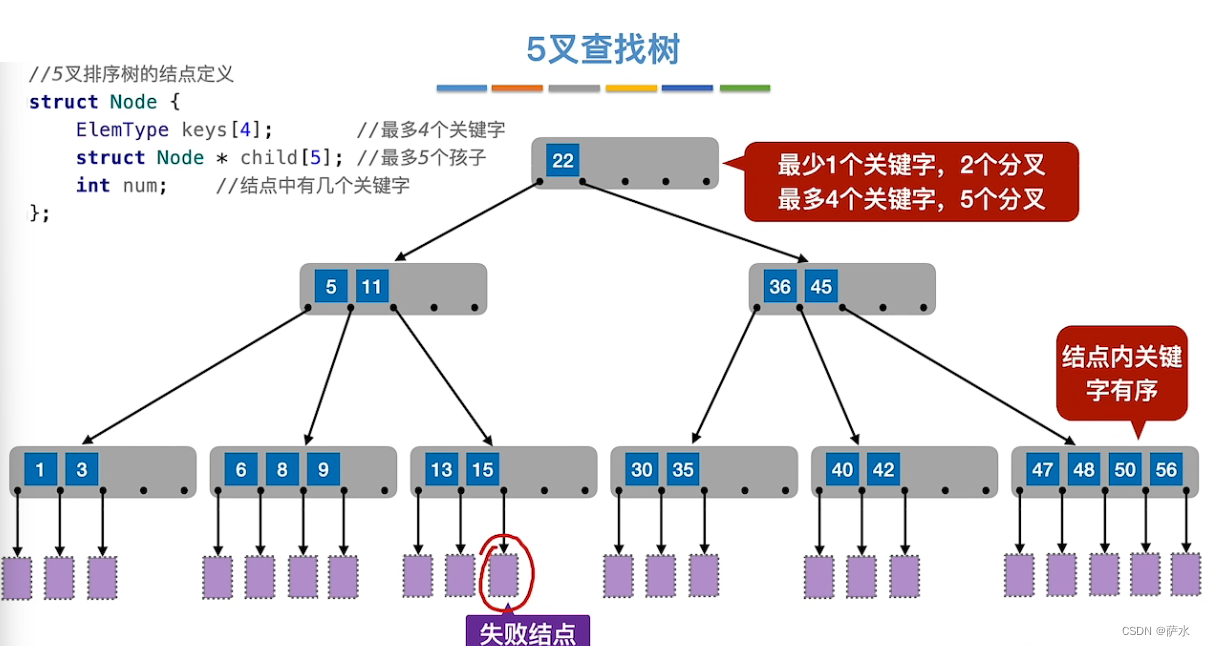
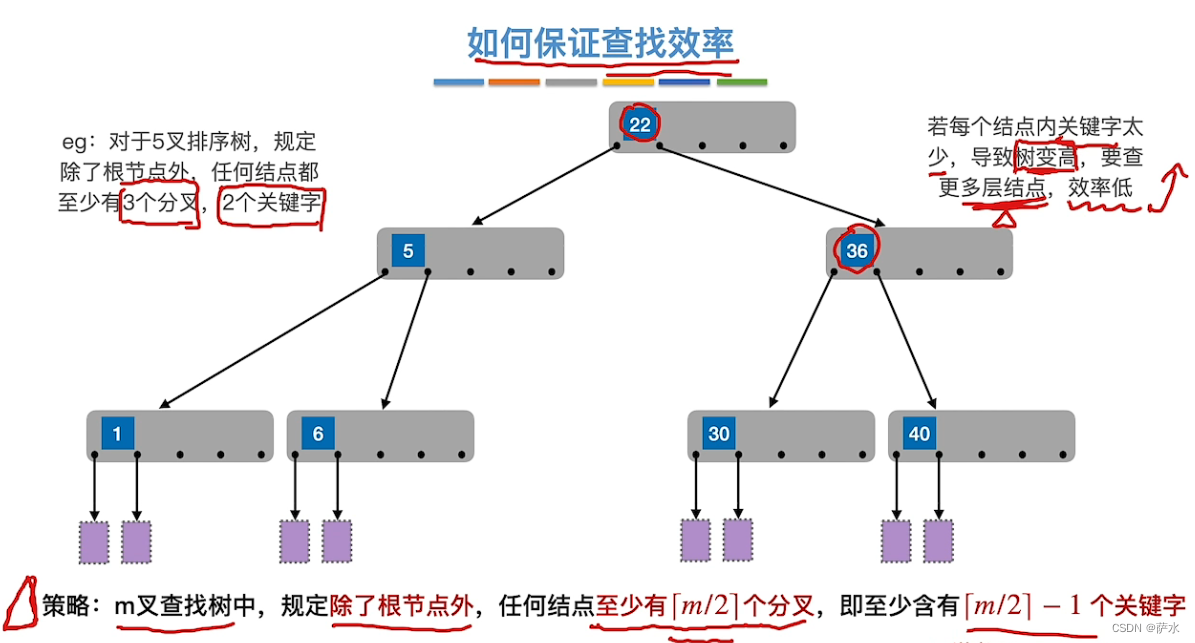
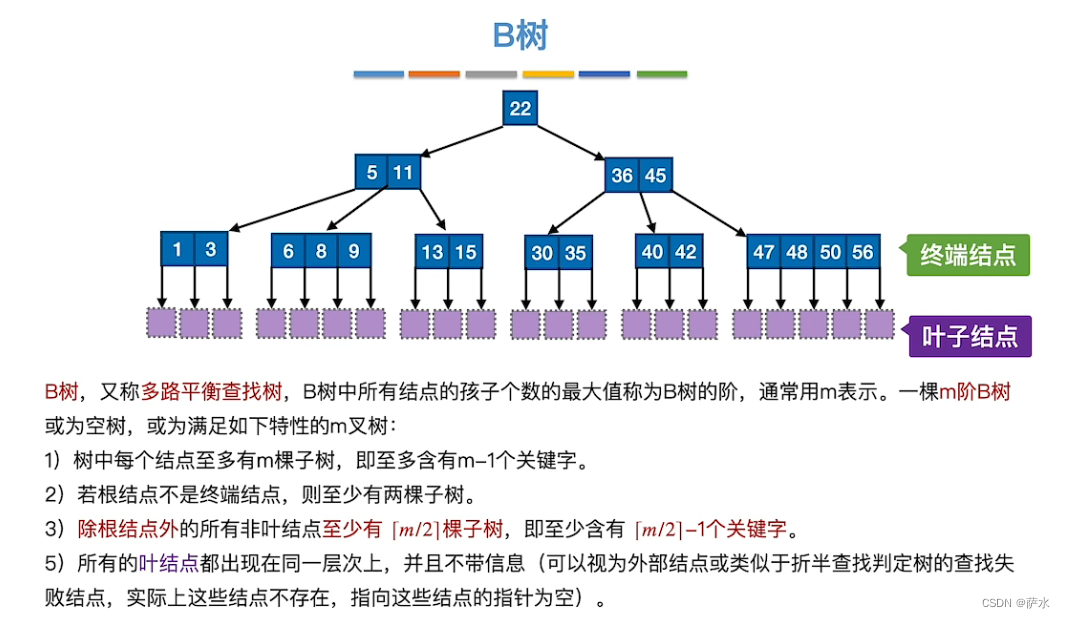
十八、B树
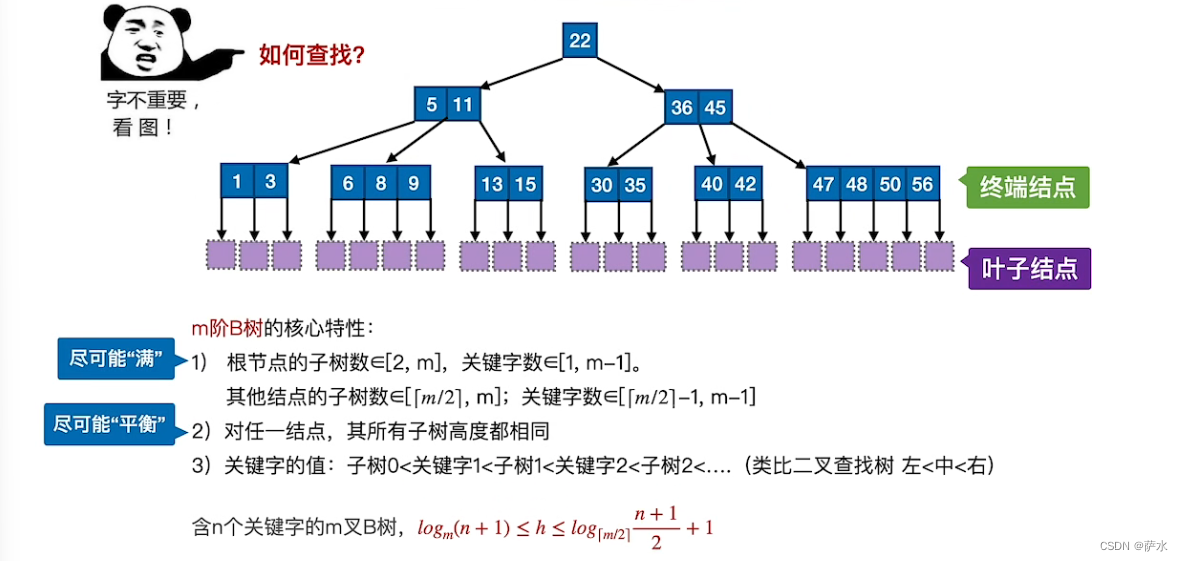
1、B树的定义
2、B树的插入删除操作
（1）插入
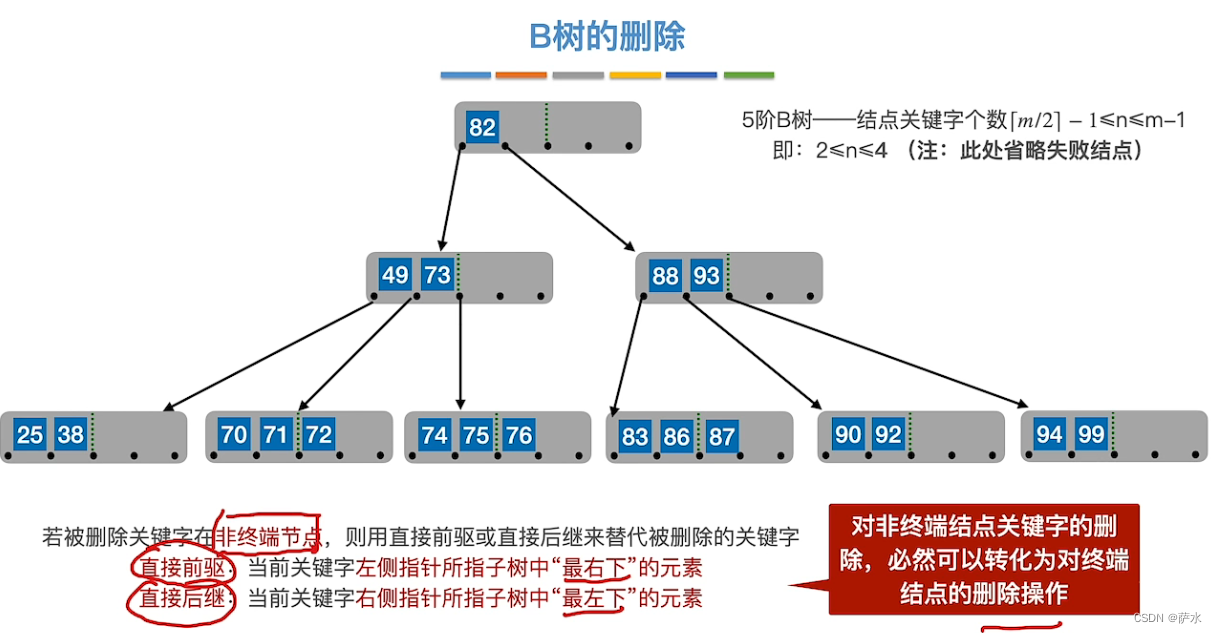
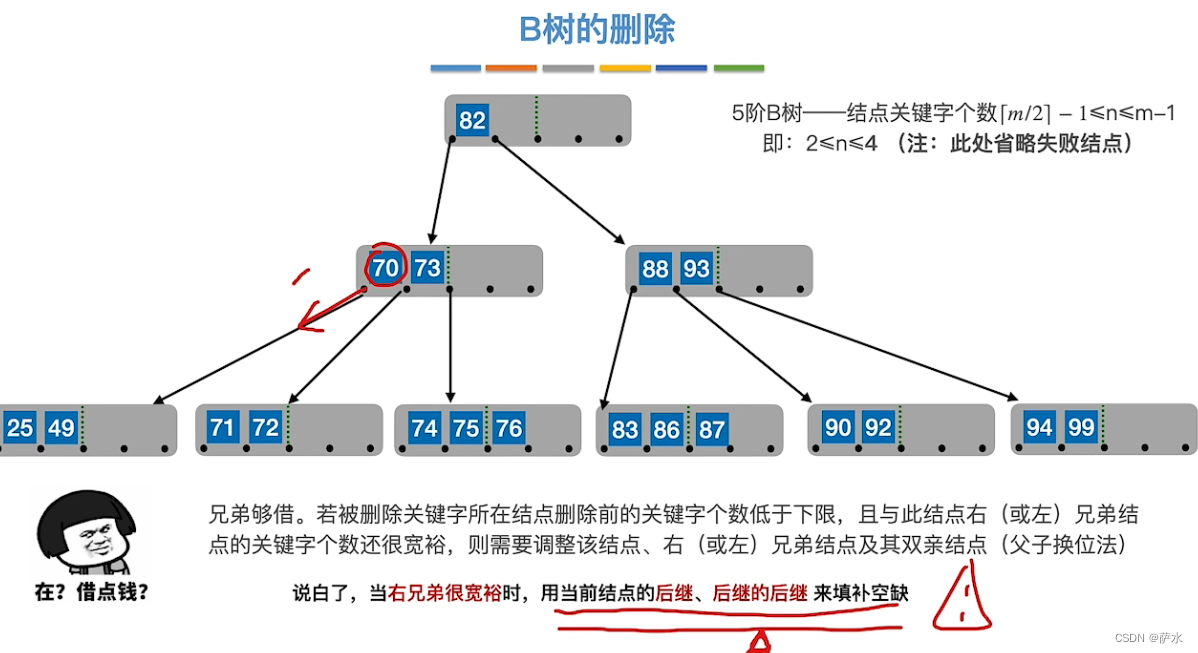
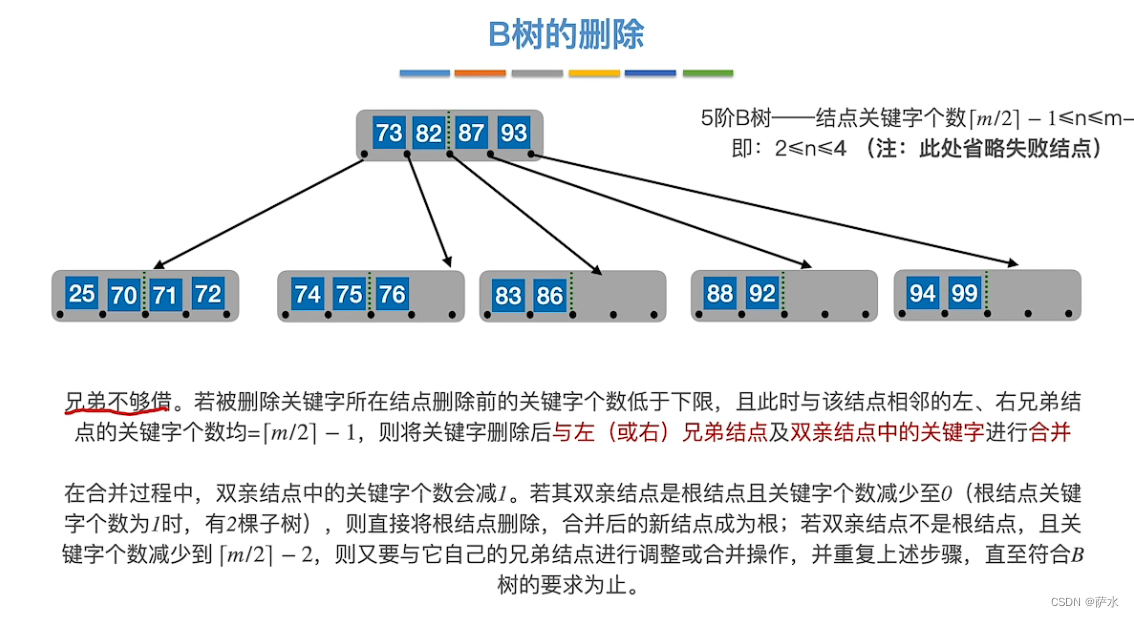
（2）删除
小结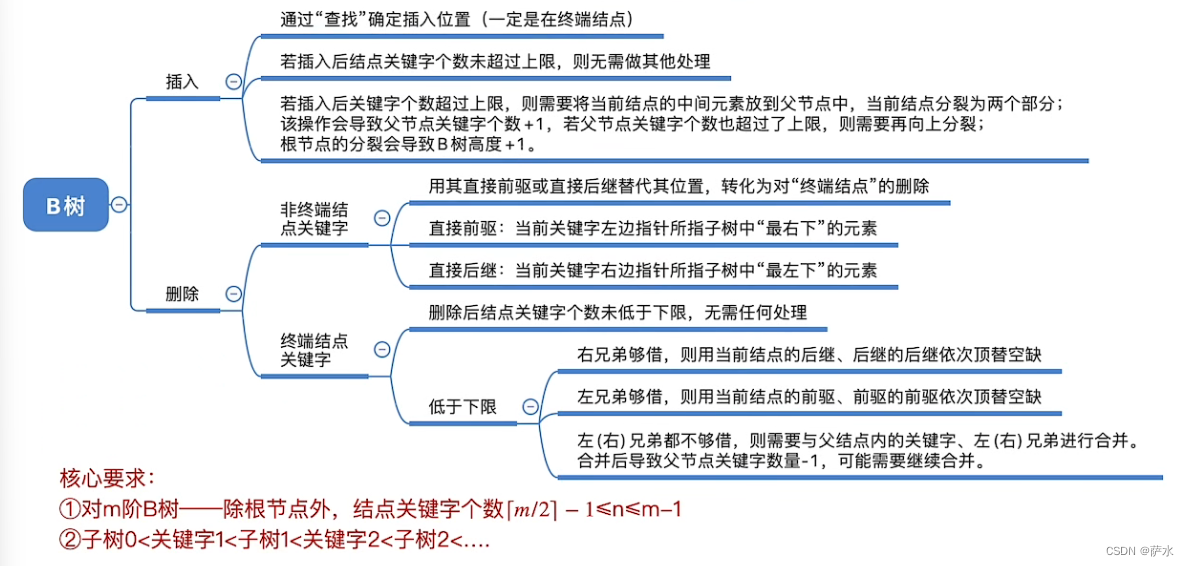
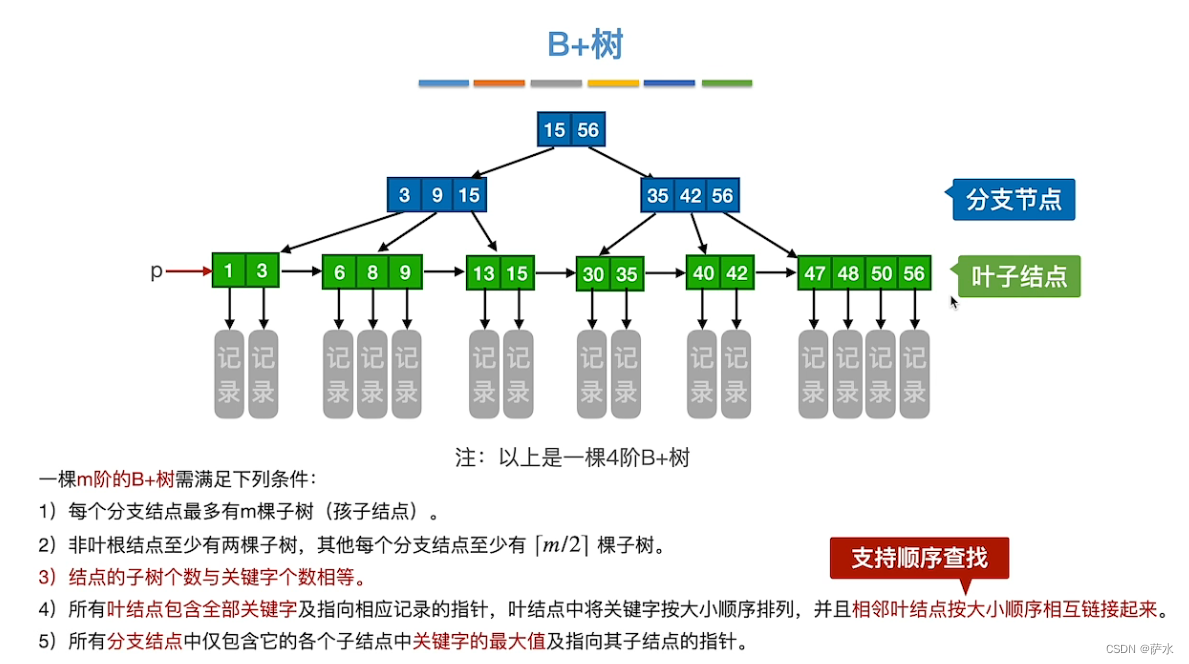
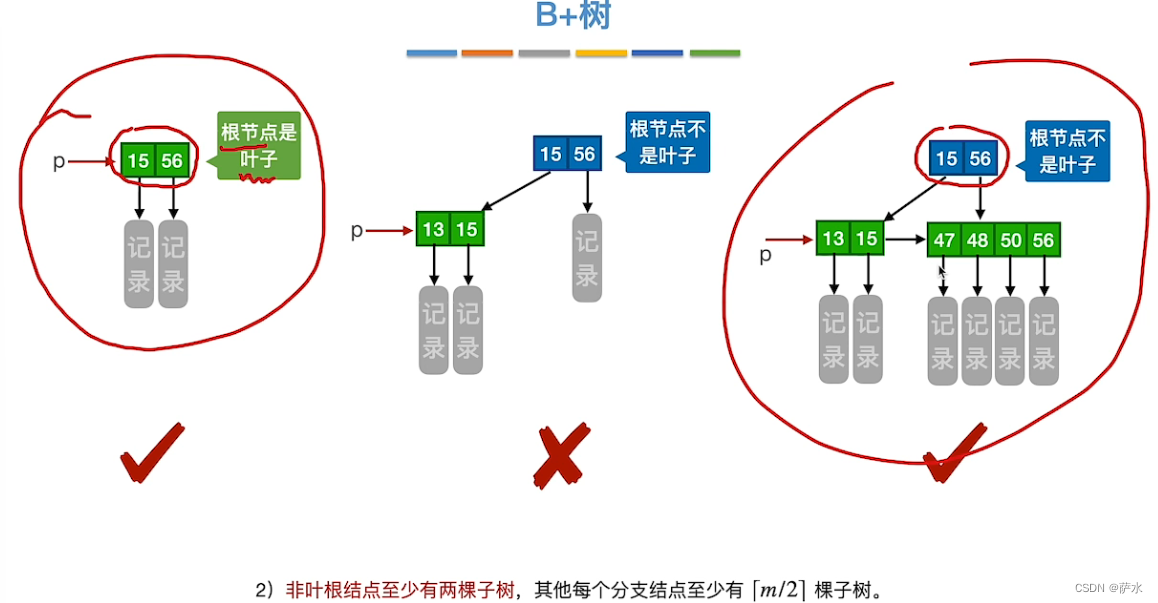
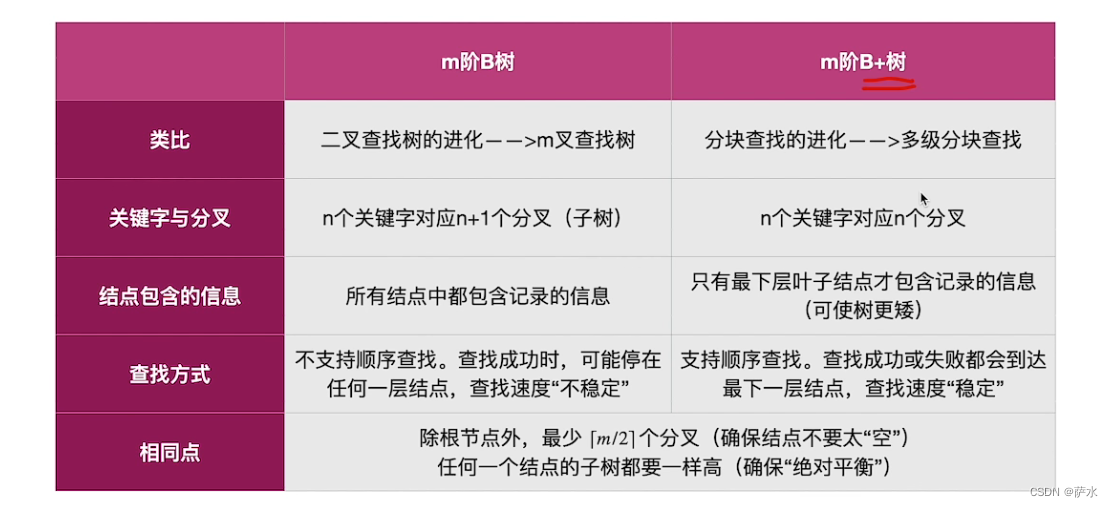
十九、B+树
