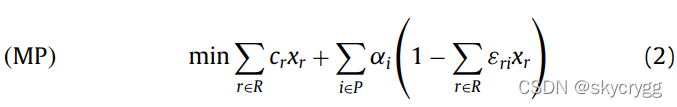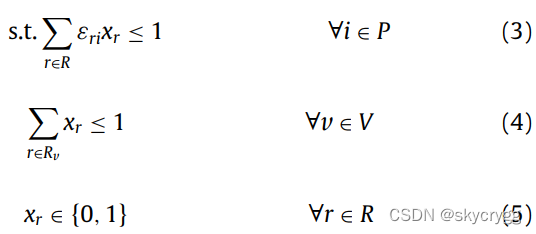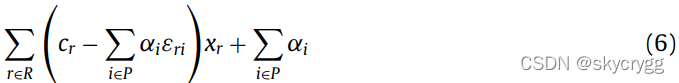PDF:A branch-and-price approach to the feeder network design problem
摘要:
考虑集装箱轮船调度问题(container liner shipping feeder network),决策变量是以中心港口(center hub)为起点和终点的多次循环中,选择哪个港口(port)去服务。考虑参数:速度参数(leg-by-leg speeds)、货物运输时间(cargo transit times)。数据来自于LinerLib benchmark。使用branch-and-price算法,在一小时内剞劂大部分算例,
介绍:
Container liner shipping 用来运输长距离的大量货物,与不定期运输(tramp shipping) 相反,需要安排船只来满足运输需求,并且轮船在固定路线上根据时间表运行。
本文考虑 Feeder Network Design Problem (FNDP),问题主要出现在对于区域供需网络中进行轮船调度路径的设计。船只主要用于从大的集散中心(hubs)提取货物,并将货物转运到小港口(ports),同时,它们从ports收集 集装箱,并重新带回 hubs。同一区域可以不止一个hub,本文只考虑一个hub的问题。
由于liner vessels根据固定时刻表(fixed schedule)进行运输,计划员对每次循环中每个port的开放时间提出一个公共时间表(public timetable),因此每个port在一个星期中有固定的一天开放。
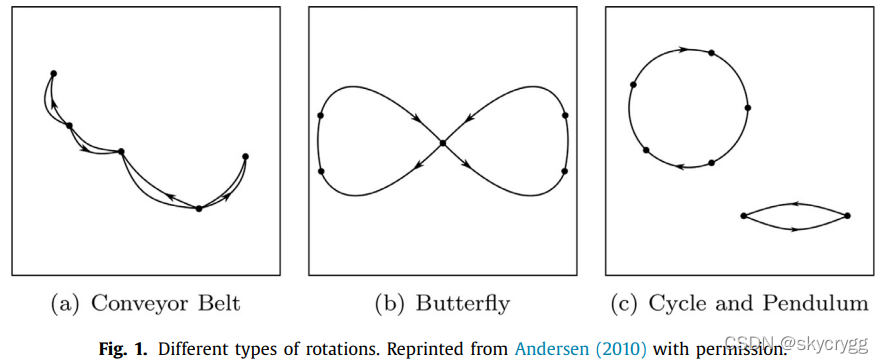
feeder network 的特性是每次循环的起点和终点都是hub port。因此可以对循环的种类分为以下三种:
(1)传送带型(2)蝴蝶型(3)循环 以及 钟摆型
决策目标:选择那些ports去服务
对于轮船公司,可以从每次服务中获得收益,同时也会由于没有服务每个port遭到惩罚;另一种可能是,雇佣别的公司的vessel进行port的服务,来赚取差价。
问题假设:已知每个port 的所有 待发送(delivery)和 待获取(pickup) 需求,需要决策的变量是,是否去该 port 进行 delivery 或 pickup (这两个决定相互独立),并且每次需要收集的货物总量都要在一次获取完毕,不允许分多个vessel进行收集。
问题目标:最大化服务货物的收益,减去 rotation次数以及 外包费用的惩罚。
rotation惩罚:port租金,调集费用 和 vessel服务费,如燃油费
外包惩罚:(1)费用持续变化;(2)受速度影响大
速度与实际费用的关系:
其中,s是实际运输速度,s*是设计速度。
约束:(1)有限容量和vessel的数量;(2)ports会在某些时间窗关闭;(3)某些物品有最大运输时间限制(防腐食品);(4)港口最大停泊量(maximum draught)
与路径(routing)问题的相关性:
1、 FNDP问题包含Capacitated VRP(Vehicle Routing Problem)问题的部分元素,包括:最大vessel容量,时间窗,vessel速度不同,带有收集和分发功能,同一hub 会有多次循环(multiple times)
the capacitated VRP since each vessel has a maximum container capacity, the VRP with time windows, the VRP with heterogeneous fleet since each vessel can differ from the others, the VRP with pickups and deliveries since we have a flow of cargo both from and to the hub, the multi-period VRP because the vehicles can get back to the hub multiple times.
2、对于VRP问题,顾客的集合是给定的不需要选择,这一点参考的是Orienteering Problem (TOP) 定向越野系列问题,对于多载具变量(multi-vehicle),一般有如下名字:Team Orienteering Problem (TOP);VRP with Profit Collection;VRP with Customer Selection.
其中,近年比较热门,包括了 time windows,pickup-and-delivery
创新点:(1)提出一个数学模型,并添加真实约束对FNDP模型进行拓展(2)提出SOTA级算法,达到与最优结果相近的结果(with very small gaps))(3)对整个前景进行分析。
2、Liner network design
Liner shipping 是遵守固定路线和给定时间表(fixed routes and published timetables)的海上货运运输,船只从管理者接受需要服务的客户信息,并在线决定需要服务哪些客户。
略
3、模型
整个计划范围被分为m个时段,;时间范围设计为一个星期的倍数,比如:如果计划范围是一个月,每个路径安排4个船,这样可以每个port一个星期访问一次。
是 区域内port的数量,包括中心hub。将每个port建模两次,一次是pickup,一次用于delivery。所有ports被定义为
其中,用于delivery;
用于pickup;
Ports i and n + i 是相同节点,只不过功能不同
集合是除了中心hub外的 所有Ports集合。每个port有最大载货量(吃水量)
,如果超过则不能进入。每个port带有装卸时间(handling time)
。由于每个port需要移动的容器数量提前已知,可以对port的
进行准确估计。其中
只与vessels种类有关,与载货量无关。
每个port有许多关闭时间窗,不仅知道port在什么时候关闭,并与一些请求相关:
(1)如果是一个在
时刻接受大量需要出口的货物的pickup port,那么
在to之前将被标记为关闭状态 ,直到
时刻可以发送。
(2)如果时间周期为2星期。delivery port 在时间
每周被服务一次。对于一些保存时间最长不超过
时间单位的货物,开放时间窗应该为
对于每个ports i,j 之间有一个对称距离(symmetric distance),这个距离满足三角不等式(两点直接距离一定不能比经过多次点后的总距离长),同一个点之间距离为0,即
,
所有 k 个vessels集合为,每个vessel v有容量
以及吃水量
,假设吃水量固定,实际中会因为容量稍微变化。每个 vessel 有速度集合
(以节为单位),
为当前速度的可能性个数。
考虑如下损失:
(1)Time charter cost:租载具费用,每日金额固定(以时间段为单位)
(2)Hotel cost:停泊费用
(3)Bunker cost:燃料费用,取决于航行速度
(4)Movement costs:搬运货物费用
(5)Fixed port call fee:呼叫服务费
(6)Variable port call fee:根据vessel容量变化的呼叫费用
服务会产生收益,以Forty-Foot Equivalent Unit (FFE)为衡量单位进行picked up 或 delivered。不同 Port 的 FFE收益不同,因此直接用表示为port
服务的总收益。相似地,对于跳过服务某port
需要赔偿
。
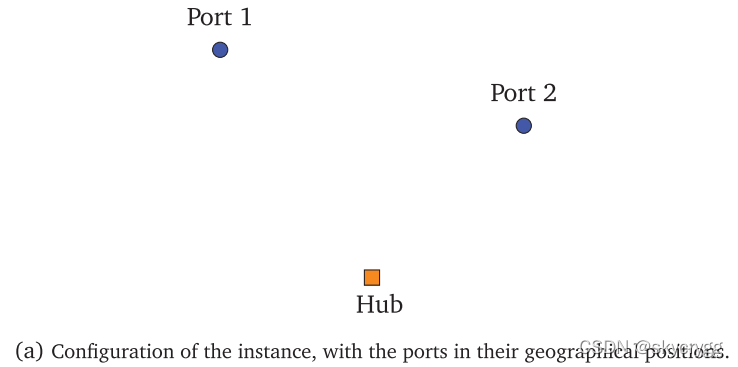
Fig. 2a 为 1 个 Hub , 2个 ports。
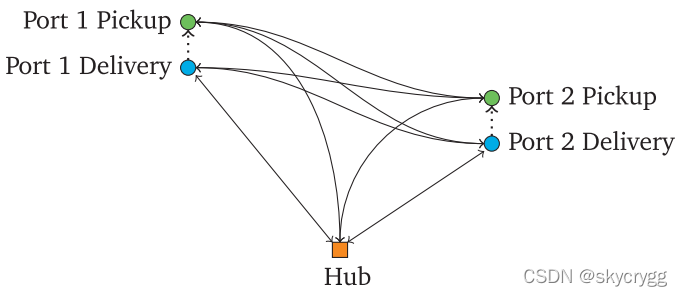
Fig. 2b 是对应生成模型。
虚线是同一个port之间的传递,首先执行的是delivery(交货),然后是pickup(取货)
3.1 图
每个vessels 有一个 space-time 图,其节点定义为:
,其中
分别是 首末节点(source and sink node)。其他点
表示一个在特定时刻的port。
被分为一下几个部分:
(1)Starting arcs: 从源节点 → 中心Hub
(2)Ending arcs: 中心Hub → 末节点
(3)Delivery-to-pickup arcs:,同一port内之间的 送货和取货
(4)Sailing arcs:不同port之间的去送货。
的到达时间为
,令
为在
处可以完成操作的时间,如果
加上处理时间依然在
开放的时间内,那么
;否则必须还要考虑等待时间(船不能停靠或操作,当port时关闭状态),因此可以创建
每个Port之间都要重复这样的计算,delivery-to-pickup 的弧同样这样计算,其中开始和结束弧是与hub相关的,开始弧表示在t 时刻离开hub,即在 [0,t] 时间段内一直等待。同样地,结束弧
:表示载具在t时刻完成rotation,并在
时刻一直等待。
一个任意弧(不同节点之间的取货和发货)的费用:
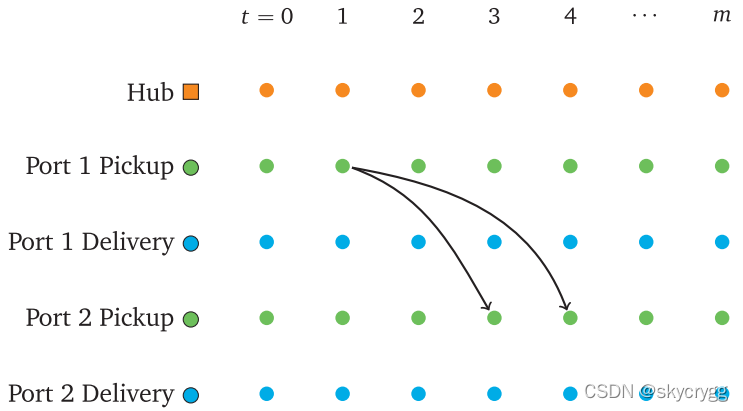
Fig. 2c 是 Fig. 2b 在时间维度上拓展的图(忽略了始末点),图中表示了
,
第一条线表示:在 time 1 离开 ,在time 2 到达
,在time 3 完成装载
第二条线表示:在 time 1 离开 ,在time 3 到达
,在time 4 完成装载
第二条线变慢的原因是:速度慢造成路途从1个时间单位→2个时间单位
3.2 Integer formulation
对每个构建一个以
为始末点的连续弧,弧在集合
内,
最多被访问一次,并且不超过容量上限, 对于每个
所有的路径记作
,
的集合为
,每条路径
的损失为
。最终,如果
在
中, 那么
,可以对FNDP建立如下模型,考虑0-1变量
,如果
是最终解的一部分,那么
=1,
目标函数(2)为最小化所选路径的总费用和惩罚,其中,后一项是如果port i 没有被服务的惩罚。
约束(3)保证每个port最多被访问一次,约束(4)表示最终解中,所有可行路径只能选择一个(不能多次使用),约束(5)则表示变量取值范围,与VRP不同,set-covering问题中,约束变量是≥(至少满足),而本问题中约束方向是≤(允许不服务)
Problem (MP)也被称为主问题(master problem),但主问题的缺点是(有效解)过大,很难去枚举全部个数,与节点个数呈指数(exponentially)增长。因此考虑用小一些的
去替代
,并且舍去对于变量的整数要求(连续化)。新的问题叫做 限制主问题 restricted master problem (RMP) ,本文提出的branch-and-price 算法,是利用 branch and bound 求解主问题:在 linear programme (RMP) 中 每个节点可以被求出,并生成新的列加入到
中。对于每个
,通过求解价格子问题
搜索可行列(promising columns)。如果子问题有负的检测数(negative reduced cost)则有继续下降的空间,加入新的列。由对偶理论可知,RMP的目标函数可以通过进基(enter the base)的方式改进,退化例子(degenerate cases)除外。如果子问题检测数全部为正,那么此时的RMP已经是最优的,也能够找到最优节点。
此时,令为约束(3)的对偶变量, 令
为约束(4)的对偶变量。目标函数可以改写为:
其中,后一项是固定值(所有未服务port的惩罚和),因此与相关的列的dual cost:
这个dual cost由原始路径cost得到;对于每个,加入了对偶价格
,移除了惩罚
;最终,是否需要支付
取决于
。
4.价格子问题(pricing subproblem)的结果
价格子问题是带有资源约束(resource constraints)的最短路径问题(SPPRC)。
的路径都是
中从源节点到终节点的路径,并且约束用来保证路径的可行性。因此,这个问题也可以看做
!!!,因为
是非循环的(acyclic),因此每条路径都是一个基本单元,本文中,每个port最多访问一次,每个节点
只能有一条出流和入流。
4.1 Greedy-randomised heuristic for the ESPPRC
我们可以通过贪婪算法找到一个从源点出发的且negative-reduced-cost的路径,然后从
条reduced cost 弧中随机选择一条不能成环的,知道到达终点
,同样这个步骤可以逆向进行。在找到路径后检查各项约束。由于这个计算时间通常很小,增加了找到可行路径的可能性。
4.2 Exact dynamic programming algorithm for the ESPPRC
ESPPRC问题可以通过动态规划精确求解,并使用label-setting算法(如,Irnich and Desaulniers, 2005),我们使用表示从源节点
到node (i, t)的每个路径。Label的设置与 Dell’Amico, Righini, and Salani (2006)中的VRP内容相似,有着相同的集合:
(1),当前节点(i, t)已经在路径中
(2),在访问当前port后,
可以取货(pick up)的量
(3), 在访问当前port后,
可以送货(deliver)的量
(4),0-1变量,当前节点访问结束后,第j项为0,则可以访问
(5),路径的cost综合,加上
费用,减去惩罚
,如果当前访问节点为终点
,还需要加上对偶价格
构造初始解:(起点为源点,可取货和送货量都为最大容量,访问节点为空),
整个解的空间为
,损失函数为
未完...................................................