977.有序数组的平方（力扣）Java-三种方法详解

题目描述

给你一个按非递减顺序排序的整数数组 nums，返回每个数字的平方组成的新数组，要求也按非递减顺序排序。
示例 1：
输入：nums = [-4,-1,0,3,10]
输出：[0,1,9,16,100]
解释：平方后，数组变为 [16,1,0,9,100]
排序后，数组变为 [0,1,9,16,100]

有序数组平方的三种解法

1. 直接排序
创建一个新数组，遍历存放原数组各数平方后值，通过Arrays.sort(新数组名);进行排序。

public int[] sortedSquares(int[] nums) {
        int[] ans = new int[nums.length];
        for (int i = 0; i < nums.length; ++i) {
            ans[i] = nums[i] * nums[i];
        }
        Arrays.sort(ans);  //Java自带数组排序方法
        return ans;
    }

2. 双指针-归并排序

归并排序：可以简单理解为将一个数组分至一定细度，通过比较排序逐步合并成完整数组。

利用数组 nums 已经按照升序排序这个条件

1. 找到原数组正数和负数的分界线下标neg
2. 将原数组平方后，0-neg是倒叙排列，(neg+1)-(n-1)是正序排列
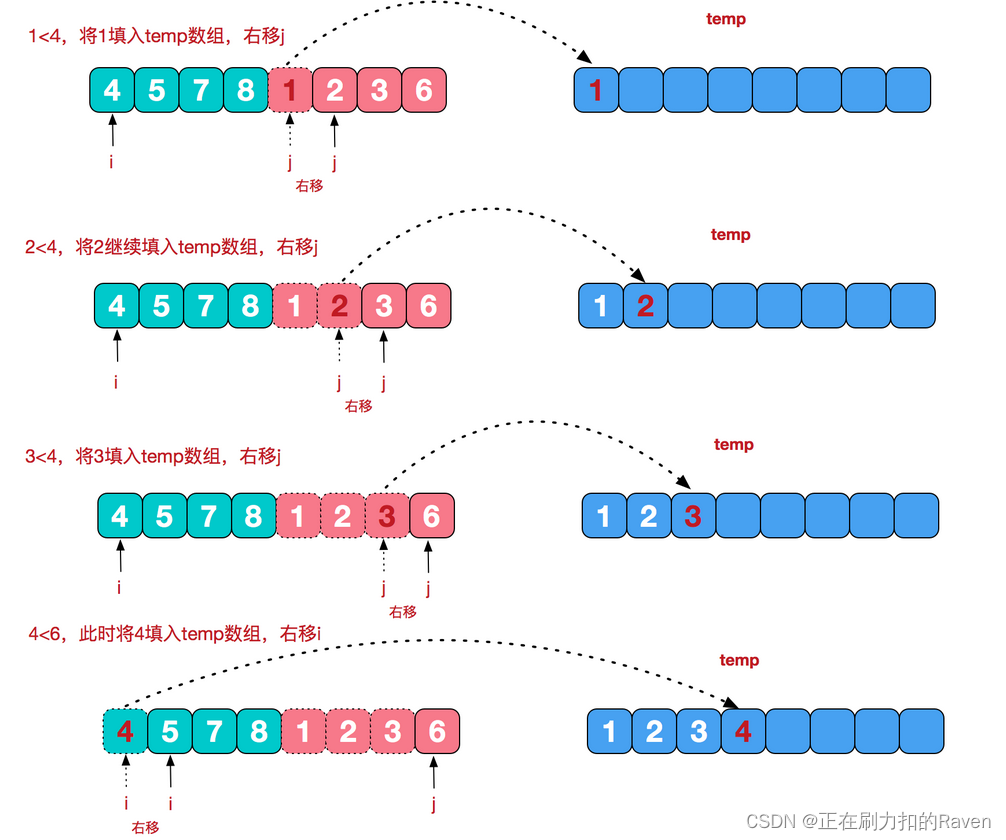
3. 利用类似归并排序算法，即依次比较原负数部分平方和正数部分平方，使用两个指针分别指向位置 neg 和neg+1，每次比较两个指针对应的数，选择较小的那个放入答案并移动指针。当某一指针移至边界时，将另一指针还未遍历到的数依次放入答案。

public int[] sortedSquares(int[] nums) {
        int n=nums.length;
		int[] ans=new int[n];
		
		int neg=-1;  //标记负数与正数的分隔下标位置
		for(int i=0;i<n;i++) {
			if(nums[i]<0) neg++;  //0-neg是负数；（neg+1）-（n-1）是正数
		}
		//将原数组平方后，0-neg是倒叙排列，(neg+1)-(n-1)是正序排列
		int negative=neg;
		int positive=neg+1;
		for(int i=0;i<n;i++) {
			nums[i]=nums[i]*nums[i];  //16,1,0,9,100,
		}
						
		int j=0;
		while(negative>=0&&positive<n) {
			if(nums[negative]<=nums[positive]) {
				ans[j++]=nums[negative];
				negative--;
			}else {
				ans[j++]=nums[positive];
				positive++;
			}
		}
		
		//将未遍历完的数组全部添加至新数组后
		if(negative>=0) {
			for(int i=j;i<n;i++) {
				ans[j++]=nums[negative--];
			}
		}else {
			for(int i=j;i<n;i++) {
				ans[j++]=nums[positive++];
			}
		}
		return ans;
    }

3. 双指针-直接比较、逆序放入
使用两个指针分别指向位置 0 和 n−1（因为平方后原负数部分递减，正数部分递增，要想获得平方后最大值需比较正数和负数部分的平方后最大值，即负数部分平方最大：nums[0]和正数部分平方最大：nums[n-1]），每次直接比较两个指针对应的数的平方值，选择较大的那个逆序放入答案并移动指针。

private static int[] sortedSquares(int[] nums) {
		int n=nums.length;
		int[] ans=new int[n];
		for(int i=0,j=n-1,k=n-1;i<=j;) { //i表示从0开始指向负数部分；j表示从n-1开始指向正数部分
			if(nums[i]*nums[i]>nums[j]*nums[j]) { //k表示从n-1开始逆序放入新数组
				ans[k]=nums[i]*nums[i];
				i++;
				k--;
			}else {
				ans[k]=nums[j]*nums[j];
				j--;
				k--;
			}
		}
		return ans;
	}