原理

设函数f(x)在[a,b]上连续，且f(a)*f(b)<0,则表明f(x)在[a,b]上至少有一个零点。
微积分中的介值定理。然后通过二分区间，缩小区间范围，当小到一定的精确度的时候，这个x就是我们所求的近似根了。

问题描述:

用二分法求下面方程在区间(a,b)之间的根：
$$2x^3-4x^2+3x-6=0$$

问题分析:

1. 区间端点a, b由用户输入（确保输入区间内有根）。
2. 计算至误差小于10^-6为止。
3. 程序中，浮点型数据应定义为双精度double类型。

二分法求方程根的步骤如下:

1. 求出给出的两个端点之间的值 $f(x$₁），$f（x$₂）。
   当 $f（x$₁）*$f（x$₂）<0，则表明 $x$₁ 和 $x$₂ 之间必存在一根；
   否则可能不存在根，则一直提示输出$x$₁ 和$x$₂ .（这也是 二分法的局限性）
2. 一旦 $f（x$₁）*$f（x$₂）<0，就表明在$x$₁和$x$₂之间有根，继续判断，求的$x$₁和$x$₂的中点值$x_0$，求出$f（x$₀）.
3. 在判断$f（x$₀）*$f（x$₁）>0,则在$x_0$和$x_2$中间去找根，此时$x_1$不起作用，用$x_0$代替$x_1$，用$f(x_0)$代替$f(x_1)$.
   要么就在$x_0$和$x_1$中去找根，此时$x_2$不起作用，用$x_0$代替$x_2$，用$f(x_0)$代替$f(x_2)$.
   

代码实现:

#include<stdio.h>  
#include<math.h> 

double f(double x); 
const double eps = 1e-6; //定义我们计算的精度

int main()
{  
	double x0,x1=0,x2=0,fx0;//[x1,x2]为寻找区间，x0为中点,浮点型数据
    scanf("%lf %lf",&x1, &x2);

    if(f(x1)*f(x2)<0)
    {
        while(fabs(x2-x1)>eps)
        {
          x0=(x1+x2)/2.0;//取x1,x2的中点
          fx0=f(x0);
          if(fabs(fx0)<eps)//满足精确度
               break;
          else if(f(x0)*f(x1)<0)
          {
              x2=x0; //修正区间，将[x1,x2]换成[x1,x0],这里的x0是中点
          }  
          else if(f(x0)*f(x2)<0)
          {
              x1=x0;//修正区间，将[x1,x2]换成[x0,x2],这里的x0是中点
          }
        }
    }
	else{
		//可以放入其他求方程的根的方法
	}

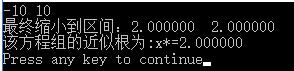
	printf("最终缩小到区间：%lf  %lf",x1,x2);
    x0=(x1+x2)/2;
    printf("\n该方程组的近似根为:x*=%lf\n",x0);

    return 0;  
}  
double f(double x) //定义函数(方程)
{
	return 2*x*x*x-4*x*x+3*x-6;
}

运行效果

参考文章

1. https://blog.csdn.net/BBHHTT/article/details/75449031
2. https://blog.csdn.net/Chen_dSir/article/details/70243602
3. https://blog.csdn.net/jiezou007/article/details/7987922